Question

Two parallel chords of a circle , 12 cm and 16 cm long are on the same of the centre. The distance between them is 2 cm. Find the radius of the circle.

Answer

10 cm

Explanation

To solve the problem of finding the radius of a circle with two parallel chords of lengths 12 cm and 16 cm, which are on the same side of the center and have a distance of 2 cm between them, we can follow these steps:

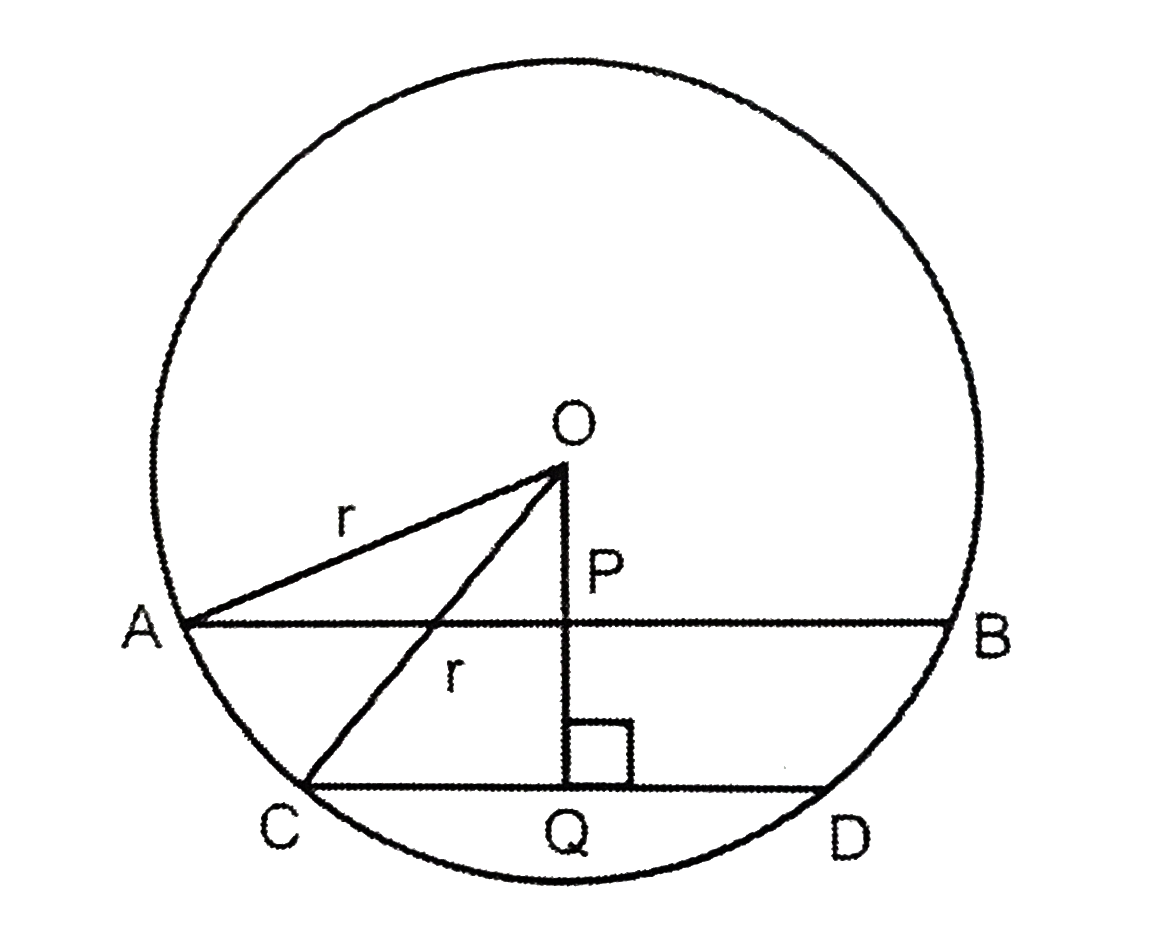
1. Draw the Circle and Chords:
- Draw a circle and label the center as O.
- Draw the longer chord (16 cm) and label its endpoints as A and B.
- Draw the shorter chord (12 cm) and label its endpoints as C and D.
- Place the chords such that they are parallel and on the same side of the center, with a distance of 2 cm between them.

2. Identify the Midpoints:
- The midpoint of chord AB (16 cm) is M, and the midpoint of chord CD (12 cm) is N.
- Since AB is 16 cm long, AM = MB = 8 cm.
- Since CD is 12 cm long, CN = ND = 6 cm.

3. Establish the Distance Between Chords:
- Let the distance from the center O to chord AB be y cm.
- Therefore, the distance from O to chord CD will be (y + 2) cm because the distance between the two chords is 2 cm.

4. Apply the Pythagorean Theorem:
- For triangle OMA (right triangle):
\( OA^2 = OM^2 + AM^2 \)
\( R^2 = y^2 + 8^2 \)
\( R^2 = y^2 + 64 \quad \text{(Equation 1)} \)

- For triangle ONC (right triangle):
\( OC^2 = ON^2 + CN^2 \)
\( R^2 = (y + 2)^2 + 6^2 \)
\( R^2 = (y + 2)^2 + 36 \)
\( R^2 = y^2 + 4y + 4 + 36 \)
\( R^2 = y^2 + 4y + 40 \quad \text{(Equation 2)} \)

5. Set the Equations Equal:
- Since both expressions equal \( R^2 \), we can set them equal to each other:
\( y^2 + 64 = y^2 + 4y + 40 \)

6. Simplify the Equation:
- Cancel \( y^2 \) from both sides:
\( 64 = 4y + 40 \)
- Rearranging gives:
\( 64 - 40 = 4y \)
\( 24 = 4y \)
\( y = 6 \)

7. Find the Radius:
- Substitute \( y \) back into Equation 1 to find \( R \):
\( R^2 = y^2 + 64 \)
\( R^2 = 6^2 + 64 \)
\( R^2 = 36 + 64 \)
\( R^2 = 100 \)
\( R = \sqrt{100} = 10 \text{ cm} \)

Final Answer:
The radius of the circle is 10 cm.