Two right triangles ABC and DBC are drawn on the same hypotenuse BC and on the same side of BC. If AC and BD intersect at P, prove that AP × PC = BP × PD.
GIVEN Right triangles ΔABCandΔDBC are drawn on the same hypotenuse BC and on the same side of BC. Also, AC and BD intersect at P.
TO PROVE AP×PC=BP×PD
PROOF In ΔBAPandΔCDP, we have
∠BAP=∠CDP=90∘
∠BAP=∠CPD (ver. opp ∠)
.∠BAP~∠CDP [ by AA- similarity]
∴APDP=BPCP
⇒AP×CP=BP×DP⇒AP×PC=BP×PD.
Hence, AP×PC=BP×PD
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Two triangles BACandBDC , right angled at AandD respectively, are drawn on the same base BC and on the same side of BC . If AC and DB intersect at P, prove that AP⋅PC=DP⋅PB.
View SolutionTwo triangles ABC and DBC are on the same base BC and on the same side of BC in which ∠A=∠D=90∘. If CAandBD meet each other at E, show that AE.EC=BE.ED.
View Solution
Knowledge Check
Two right triangles ABC and DBC are drawn on the same hypotenues BC on the same side of BC. If AC and DB intersects at P, then :
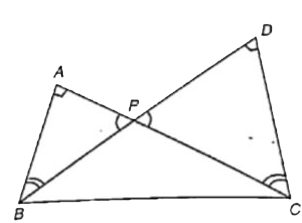 AAPPC=BPDPBAP×DP=PC×BPCAP×PC=BP×DPDAP×BP=PC×PD
AAPPC=BPDPBAP×DP=PC×BPCAP×PC=BP×DPDAP×BP=PC×PD
△ABC and △DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that (i) △ABD≅△ACD (ii) △ABP≅△ACP (iii) AP bisects ∠A as well as △D. (iv) AP is the perpendicular bisector of BC.
View SolutionIn figure ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.

View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E show that
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
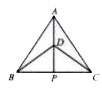
AP bisects ∠A as well as ∠D.
View SolutionIn Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)= AODO
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
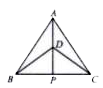
ΔABP≅ΔACP
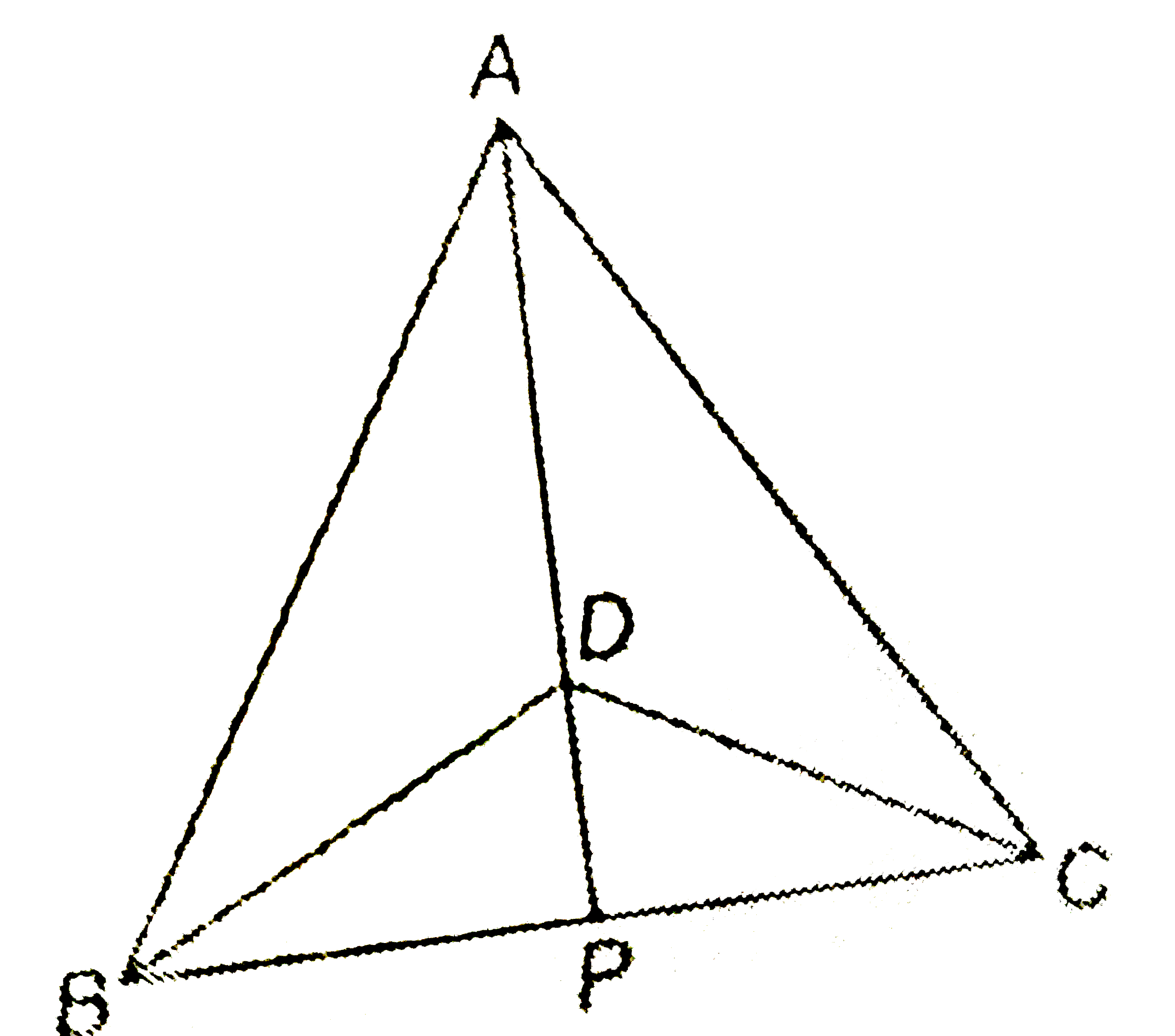
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
View Solution