Two tangents making an angle of 1200 with each other are drawn to a circle of radius 6cm, then the length of each tangent is equal to √3 cm (b) 6 √3 cm (c) √2 cm (d) 2 √3 cm
We have,
Let the center of circle be O.
Let the tangents be PA and PB from point P into the circle .
OA=OB=radius=6cm.
Then,
In the triangle OAP and OBP:
∠OAP=∠OBP=90∘
∠OPA=∠OPB=120∘2=60^@<br>∠POA=∠POB=(120^@)/2=30^@<br>Tan60=OAPAPA=OA cot 60^@=6/(sqrt3)=2sqrt3<br>Then,<br>The≤n>hoftan≥nt =2sqrt3cm.
Topper's Solved these Questions
Similar Questions
Two tangents making an angle of 1200 with each other are drawn to a circle of radius 6cm, then the length of each tangent is equal to √3 cm (b) 6 √3 cm (c) √2 cm (d) 2 √3 cm
View SolutionTwo tangents making an angle of 60∘ between them, are drawn to a circle of radius √2 cm, then find the length of each tangent.
View Solution
Knowledge Check
- Question 1 - Select One
IF two tangents inclined at an angle of 60∘ are drawn to a circle of radius 3 cm , then the length of each tangent is equal to
A3√32 cmB6 cmC3 cmD3√3cm - Question 2 - Select One
If two tangents inclined at an angle of 60∘ are drawn to a circle of radius 4 cm, then the length of each tangent is equal to :
A2√3 cmB8 cmC4 cmD4√3 cm - Question 3 - Select One
If two tangents inclined at an angle of 60∘ are drawn to a circle of radius 3cm then the length of each tangent is
A3cmB3√32cmC3√3cmD6cm
If two tangents inlined at an angle 60∘ are drawn to a circle of radius 3 cm , then the length of each tangent is equal to :
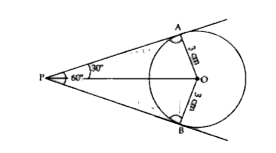 View Solution
View SolutionIf two tangents inclined at an angle 60∘ are drawn to a circle of radius 3 cm, then, the length of each tangent is equal to
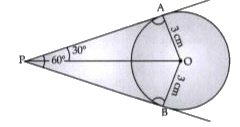 View Solution
View SolutionIf two tangents inclinced at an angle 60∘ are drawn to a circle of radius 3 cm, then find the length of each tangent.
View SolutionIf two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then what is the length of each tangent ?
View SolutionIf the surface area of a cube is 13254 cm2, then the length of its diagonal is 44√3cm (b) 45√3cm (c) 46√3cm (d) 47√3cm
View Solution

