Two vertices of an equilateral triangle are (−1,0) and (1,0), and its third vertex lies above the x-axis. The equation of its circumcircle is ____________
A
x2+y2=1
B
√3(x2+y2)+2y−√3=0
C
√3(x2+y2)−2y−√3=0
D
none of these
Video Solution
Text Solution
The correct Answer is:C
We have equilateral triangle ABC.
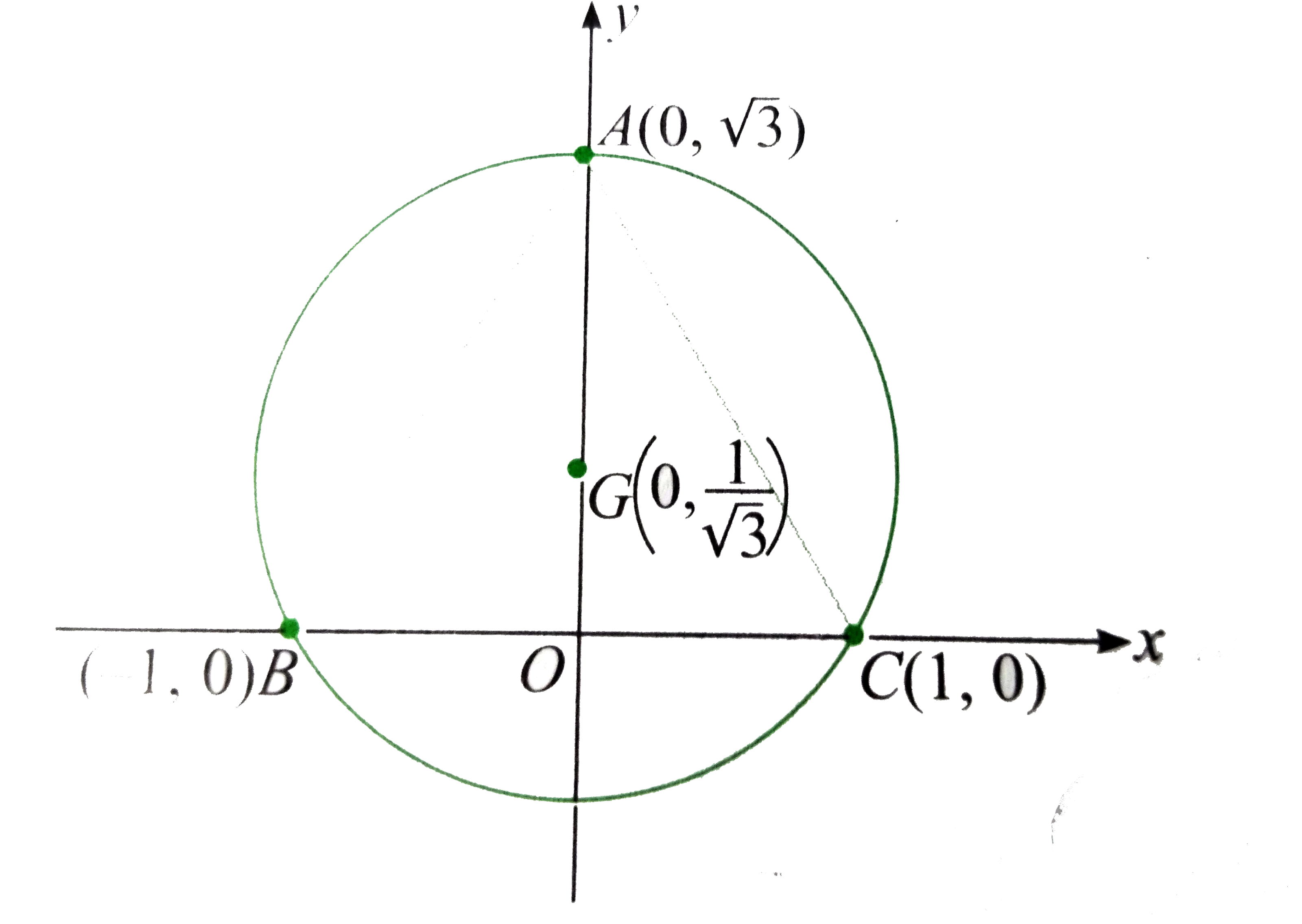
Let B≡(−1,0),C≡(1,0).
Then A lies on y-axis.
∴OA=ABsin60∘=√3
∴A≡(0,√3)
In an equilateral triangle, circumcentre coincides with centroid.
Thus, circumcentre of triangle ABC is G≡(−1+1+03,√3+0+03)≡(0,1√3)
Circumradius =AG=√3−1√3=2√3
Therefore, equation of circumcircle of triangle ABC is (x−0)2+(y+1√3)2=(2√3)2
|
Topper's Solved these Questions
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise 4.1
Explore 14 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise 4.2
Explore 5 Videos
- BINOMIAL THEORMBook:CENGAGEChapter:BINOMIAL THEORMExercise:Question Bank
Explore 31 Videos
- CIRCLESBook:CENGAGEChapter:CIRCLESExercise:Question Bank
Explore 32 Videos
Similar Questions
Knowledge Check
If two vertices of an equilateral triangle are (1,1)and(−1,1) then the third vertex may be
A(−√3,−√3)B(−√3,√3)C(√3,−√3)D(√3,√3)If two vertices of an equilateral triangle are A(−a,0)andB(a,0),a>0, and the third vertex C lies above y-axis, then the equation of the circumcircle of ΔABC is :
A3x2+3y2−2√3ay=3a2B3x2+3y2−2ay=3a2Cx2+y2−2ay=a2Dx2+y2−√3ay=a3If the centroid of an equilateral triangle is (2, -2) and its one vertex is (-1, 1) , then the equation of its circumcircle is
Ax2+y2−4x+4y−10=0Bx2+y2+4x−4y+10=0Cx2+y2+4x−4y−10=0Dx2+y2+4x+4y+10=0
Two vertices of an equilateral triangle are (0,0)and(0,2√3). Find the third vertex
View SolutionIf the two vertices of an equilateral triangle be (0,0),(3,√3), find the third vertex.
View SolutionTwo vertices of an equilateral triangle are (-4,-4),(4,4) and its incenter is (−13,13) .The third vertex
View SolutionTwo vertices of an equilateral triangle are (-4,-4),(4,4) and its incenter is (−83,83) .The third vertex is
View SolutionTwo vertices of a triangle are (-1,4) and (5, 2), If its centroid is (0,-3), then the third vertex is
View Solution