What is the angle substended by an edge of regular tetrahedron at its centre?

A

$\cos^{- 1} (\frac{- 1}{2})$

B

$\cos^{- 1} (\frac{- 1}{\sqrt{2}})$

C

$\cos^{- 1} (\frac{- 1}{3})$

D

$\cos^{- 1} (\frac{- 1}{\sqrt{3}})$

Text Solution

Verified by Experts

The correct Answer is:C

$\vec{a}, \vec{b}, \vec{c}$
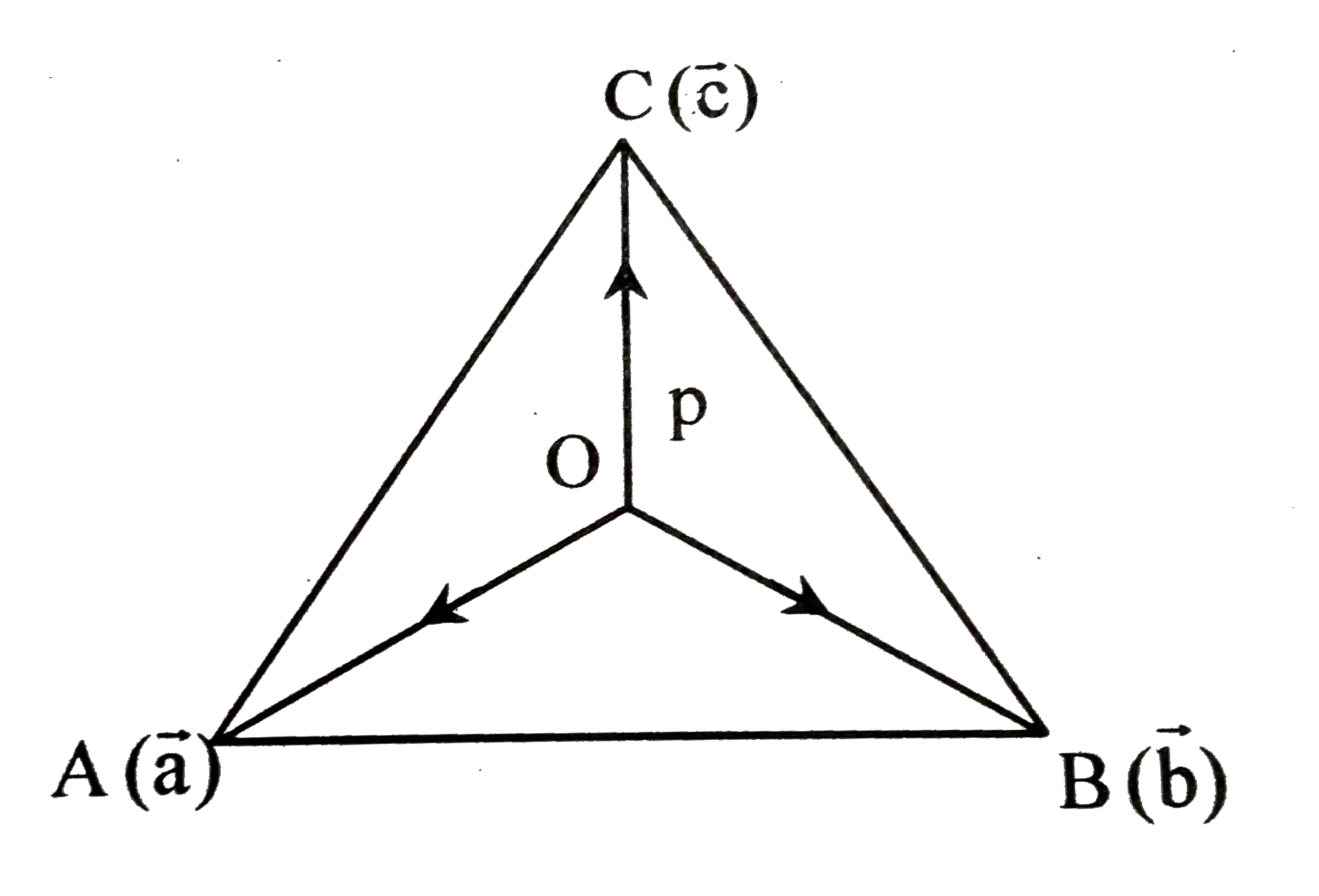
are unit vector
$\vec{a} \land \vec{b} = \vec{b} \land \vec{c} = \vec{c} \land \vec{a} = \frac{π}{3}$
centre p $(\frac{\vec{o} + \vec{a} + \vec{b} + \vec{c}}{4})$
Now angle between $\vec{A P} & \vec{B P}$
$\cos θ = \frac{\vec{A P} \cdot \vec{B P}}{| \vec{A P} | ∣ \vec{B P}} = \frac{(\frac{\vec{a} + \vec{b} + \vec{c}}{4} - \vec{a}) \cdot (\frac{\vec{a} + \vec{b} + \vec{c}}{4} - \vec{b})}{| \frac{\vec{a} + \vec{b} + \vec{c}}{4} - \vec{a} | | \frac{\vec{a} + \vec{b} + \vec{c}}{4} - \vec{b} |}$
$= \frac{(\vec{b} + \vec{c} - 3 \vec{a}) \cdot (\vec{a} + \vec{c} - 3 \vec{b})}{| \vec{b} + \vec{c} - 3 \vec{a} | \cdot | \vec{a} + \vec{c} - 3 \vec{b} |}$
$= \frac{\vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} - 3 \vec{b^{2}} + \vec{a} \cdot \vec{c} + \vec{c^{2}} - 3 \vec{b} \cdot c - 3 \vec{a^{2}} - 3 \vec{a} \cdot \vec{c} + 9 \vec{a} \cdot \vec{b}}{(\vec{b^{2}} + \vec{c^{2}} + 9 \vec{a^{2}} + 2 \vec{b} \cdot \vec{c} - 6 \vec{a} \cdot \vec{c} - 6 \vec{a} \cdot \vec{b})}$
$\frac{\frac{1}{2} + \frac{1}{2} - 3 + \frac{1}{2} + 1 - \frac{3}{2} - 3 - \frac{3}{2} + \frac{9}{2}}{1 + 1 + 9 + 1 - 3 - 3}$
$= \frac{- 5 + 3}{6} = - \frac{1}{3}$
$θ = \cos^{- 1} (- \frac{1}{3})$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

The acute angle betwene any two faces of a regular tetrahedron is
A ${cos}^{- 1} (\frac{1}{3})$
B ${cos}^{- 1} (\frac{1}{\sqrt{3}}$
C ${cos}^{- 1} (\frac{2}{3})$
Dnone of these
Each edge of a regular tetrahedron is 3 cm, then its volume is
A $\frac{9 \sqrt{2}}{4}$ c.c
B $27 \sqrt{3}$ c.c.
C $\frac{4 \sqrt{2}}{9}$ c.c.
D $9 \sqrt{3}$ c.c.
What is the solid angle subtended by a hemisphere at its centre?
A $π$ steradian
B $2 π$ steradian
C $3 π$ steradian
D $4 π$ steradian

KVPY PREVIOUS YEAR-KVPY-PART -I MATHEMATICS

Home
Ask Doubt
Profile