Which of the following relations are functions ?
y is a Maths pupil of x, where x represents any Maths teacher in a school.
To determine whether the relation "y is a Maths pupil of x, where x represents any Maths teacher in a school" is a function, we need to analyze the definition of a function.
1. Understanding the Relation:
- We have a relation where x represents Maths teachers and y represents Maths pupils.
- The relation states that y is a pupil of x.
2. Definition of a Function:
- A relation is a function if every element in the domain (in this case, Maths teachers) is associated with exactly one element in the range (Maths pupils).
3. Analyzing the Relation:
- Let's denote the Maths teachers as x1, x2, x3, etc., and the Maths pupils as y1, y2, y3, etc.
- A Maths teacher (e.g., x1) can teach multiple pupils (e.g., y1, y2, y3).
- Conversely, a pupil (e.g., y1) can have multiple teachers (e.g., x1, x2).
4. Checking for Multiple Associations:
- If a single Maths teacher (x1) can have multiple pupils (y1, y2), then x1 is associated with more than one y value.
- This means that for the same x (teacher), there are multiple y (pupils), which violates the definition of a function.
5. Conclusion:
- Since a Maths teacher can have multiple pupils, the relation "y is a Maths pupil of x" does not satisfy the criteria for being a function.
- Therefore, this relation is not a function.
- We have a relation where x represents Maths teachers and y represents Maths pupils.
- The relation states that y is a pupil of x.
- A relation is a function if every element in the domain (in this case, Maths teachers) is associated with exactly one element in the range (Maths pupils).
- Let's denote the Maths teachers as x1, x2, x3, etc., and the Maths pupils as y1, y2, y3, etc.
- A Maths teacher (e.g., x1) can teach multiple pupils (e.g., y1, y2, y3).
- Conversely, a pupil (e.g., y1) can have multiple teachers (e.g., x1, x2).
- If a single Maths teacher (x1) can have multiple pupils (y1, y2), then x1 is associated with more than one y value.
- This means that for the same x (teacher), there are multiple y (pupils), which violates the definition of a function.
- Since a Maths teacher can have multiple pupils, the relation "y is a Maths pupil of x" does not satisfy the criteria for being a function.
- Therefore, this relation is not a function.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2 (a)24videos
RELATIONS AND FUNCTIONS
- BOOK - ICSECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2 (b)26videos
RELATIONS AND FUNCTIONS
- BOOK - ICSECHAPTER - RELATION AND FUNCTIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (Choose the correct answer from the given four options in questions)32videos
RELATION AND FUNCTIONS
- BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 01EXERCISE - SECTION C8videos
SAMPLE QUESTION PAPER 01
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following is not related to sex chromosome X or Y?
ATurner's syndromeBKlinefelter's syndromeCDown's syndromeDHaemophilia and colour blindness
Which of the following can represent a linear function for each x∈R ?
View SolutionDoes the following graph represent a function or a relation?
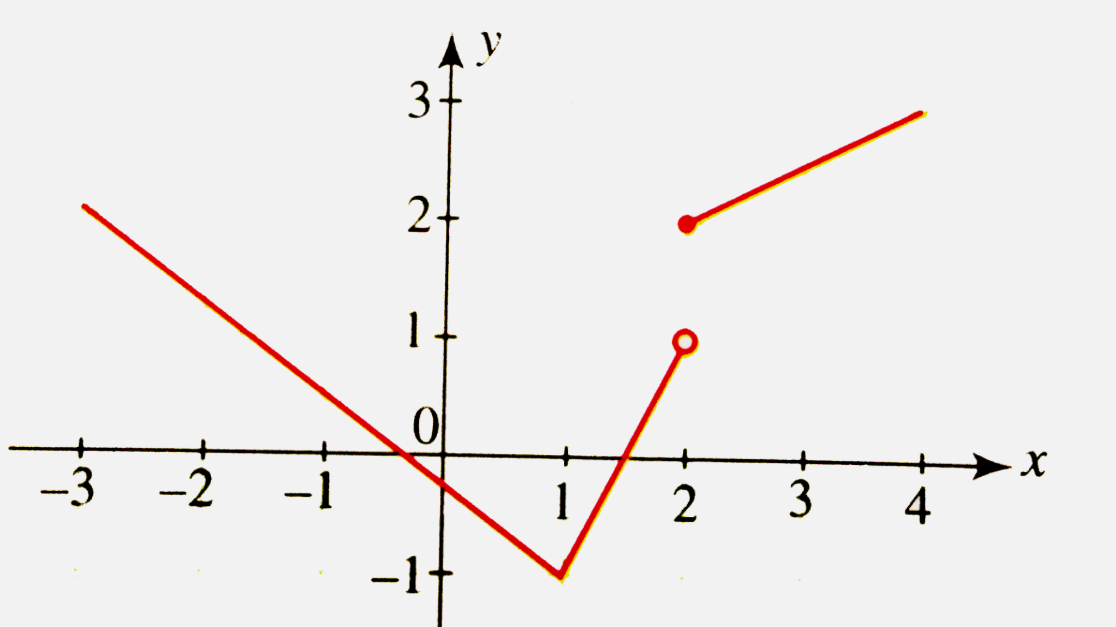 View Solution
View SolutionDraw the graph of |y|=[x], where [.] represents the greatest integer function.
View SolutionDraw the graph of y={|x|}, where {.} represents the fractional part function.
View SolutionDraw the graph of |y|={x}, where {.} represents the fractional part function.
View SolutionState for each of the following relations whether it is function or not. (Write Yes or No)
{(x,y):x∈A,y∈B,y is the area of a square of side x} where A is the set of measurements of length.View SolutionState for each of the following relations whether it is function or not. (Write Yes or No)
{(x,y):x∈B,y∈P,y is a passenger on x} where B is the set of buses of a school and P is set of pupils of some schools.View Solution

