While calculating mode the following observation are found. Lower limit of modal class =40, frequency of modal class =20, frequency of previous class =12 , frequency of preceding class =11 and width of the class =10, find mode .
The correct Answer is:44.71
To find the mode using the given data, we will use the formula for mode in a grouped frequency distribution:
Mode=L+f1−f0(2f1−f0−f2)×h
Where:
- L = lower limit of the modal class
- f1 = frequency of the modal class
- f0 = frequency of the preceding class
- f2 = frequency of the succeeding class
- h = width of the class
1. Identify the values from the problem:
- Lower limit of modal class L=40
- Frequency of modal class f1=20
- Frequency of preceding class f0=12
- Frequency of succeeding class f2=11
- Width of the class h=10
2. Substitute the values into the mode formula:
Mode=40+20−12(2×20−12−11)×10
3. Calculate the numerator:
20−12=8
4. Calculate the denominator:
2×20−12−11=40−12−11=17
5. Now substitute these results back into the formula:
Mode=40+817×10
6. Calculate 817×10:
8×1017=8017
7. Now, calculate 40+8017:
- First, convert 40 into a fraction with a denominator of 17:
40=68017
- Now add:
Mode=68017+8017=76017
8. Finally, divide to find the mode:
76017≈44.71
Final Answer:
The mode is approximately 44.71.
- L = lower limit of the modal class
- f1 = frequency of the modal class
- f0 = frequency of the preceding class
- f2 = frequency of the succeeding class
- h = width of the class
- Lower limit of modal class L=40
- Frequency of modal class f1=20
- Frequency of preceding class f0=12
- Frequency of succeeding class f2=11
- Width of the class h=10
Mode=40+20−12(2×20−12−11)×10
20−12=8
2×20−12−11=40−12−11=17
Mode=40+817×10
8×1017=8017
- First, convert 40 into a fraction with a denominator of 17:
40=68017
- Now add:
Mode=68017+8017=76017
76017≈44.71
The mode is approximately 44.71.
Topper's Solved these Questions
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Short Answer Questions
5 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - EXERCISE 14 E
5 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Long Answer Questions
5 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions
1 Videos
Similar Questions
For the following frequency distribution

The upper limit of median class is
View SolutionFor the following distribution

the sum of lower limits of the median class and modal class is
View SolutionWrite the modal class of the following distribution :

View SolutionConsider the following frequency distribution

The upper limit of the median class in
View SolutionFor the following distribution

the modal class is
View SolutionThe starting value of the model class of a distribution is 20. The frequency of the model class is 18. The frequencies of the classes preceeding and succeeding are 8,10 and the width of the model class is 5, then mode is
View SolutionConsider the following distribution
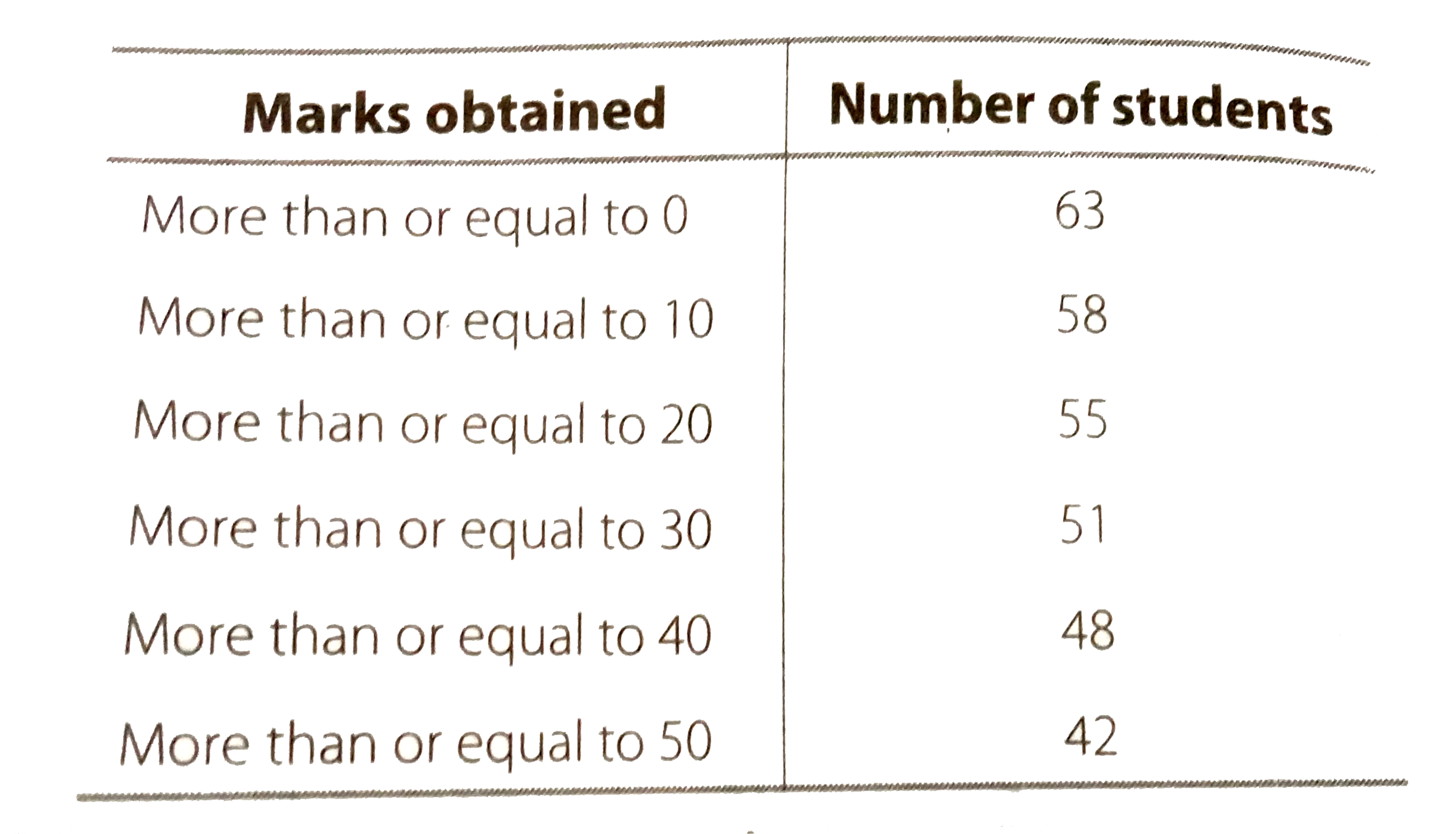
Frequency of the class 30-40 is
View SolutionFrom a frequency distribution, c = 3, l = 65 . 5 f = 42, m = 23, N = 102 then median is (l = lower limit of the median class, m= cumulative frequency of the class preceeding the median class, N = total frequency, f = frequency of the median class, c = width of the median class)
View SolutionConsider the data

The frequency of the upper limit of the median class and the lower limit of the modal class is
View SolutionIn the following data, find the values of a and b . Find the median class modal class :

View Solution
