Complete Solutions to SECTION - B of chapter REVISION PAPER -3 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | REVISION PAPER -3 |
| SELINA PUBLICATION | SECTION - B |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
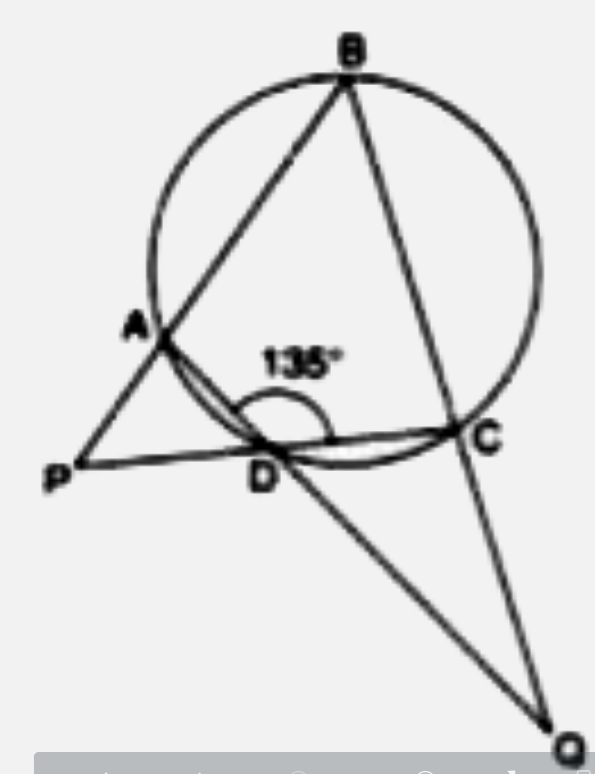
ABCD is a syclic quadrilateral with `angle ADC =135^(@).` Sides BA and CD produced meet at point P, sides AD and BC produced meet at point `Q. If angle P: angle Q = 2:1,` find angles P and Q.
View SolutionA right circular cone is 3.6 cm high and radius of its base is 1.6 cm. It is melted and recast into a right circular cone with radius of its base as 1.2 cm. Find its height.
View SolutionIn `GP.2,6,18,54……………13122,` the product of `3 ^(rd)` term from the beginning and `3 ^(rd)` term from the last is 26244. Show It.
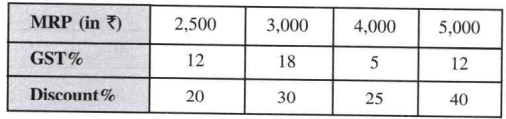
View SolutionFor the inter-state supply of the following godds/services, find the amount of bill:
View SolutionIs the line through `(-2,3) and (4,1)` perpendicular to the line `3x =y + 1?` Does the line `3x = y +1` bisect the join of `(-2,3) and (4,1)?`
View SolutionIf the roots of the equation `(b-c)x^2+(c-a)x+(a-b)=0` are equal, then prove that `2b=a+cdot`
View SolutionIn a positive fraction, the denominator is greater than the numerator by 3, If 1 is subtracted from both the numerator and the denominarot, the fraction is decreases by `(1)/(14).` Find the fraction.
View SolutionSolve :
(i) `(x^(2)-x)^(2)+5(x^(2)-x)+4=0`
(ii) `(x^(2)-3x)^(2)-16(x^(2)-3x)-36=0`
View SolutionIf `-5` is a root of the quadratic equation `2x^2+p x-15=0` and the quadratic equation `p(x^2+x)+k=0` has equal roots, find the value of `kdot`
View SolutionThere are three containers of equal capacity and all are completely filled with mixtures of acid and water in different ratios. The ratio of acid to water in the first container is 2 : 3, in the second container the ratio is 3:7 and in the third container it is 4:11. If the mixtures of all the three containers are mixed together, what will be the ratio of acid to water in it?
View SolutionA straight line passes through the points A(-5, 2) and B(3,-6). It intersects the co-ordinate axes at points C and D . Find :
the equation of AB.
View SolutionA straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find :
the co-ordinates of points C and D.
View SolutionA straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find :
the co-ordinates of point M.
View SolutionIf `(7a + 8b)/( 7c + 8d) = (7a - 8b)/(7c - 8d),` prove that :
`a:b= c:d`
View SolutionIf `(7a + 8b)/( 7c + 8d) = (7a - 8b)/(7c - 8d),` prove that :
(i)`a:b=c:d`
(ii) `(4a - 5b)/(4c - 5d)= (3a + 4b)/(3c + 4d)`
View SolutionCalculate the ratio in which the line joining `A(5, 6) and B(-3, 4)` is divided by `x = 2`. Also, find the point of intersection.
View SolutionThe speed of a boat in still water is 15 km/hr. It can go 30 km upstream and return downstream to the original point in 4 hours 30 minutes. Find the speed of the stream.
View SolutionProve that :` sin A (1 + tan A) + cos A (1 + cot A) = sec A + cosec A.`
View SolutionIf `x in W,` find the solution set of `(3)/(5) x - ( 2x -1)/(3) gt1.`
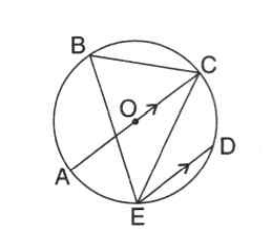
View SolutionThe figure alongside shows a circle with centre 0. Chord ED is parallel to diameter AC and angle `CBE = 65^(@).` Find angle CED.
View SolutionThe sum of `3^(rd) and 11^(th)` terms of an A.P. is 34. Find the sum of its 13 terms.
View SolutionSum of the first p, q and r terms of an A.P are a, b and c, respectively.Prove that `a/p(q-r)+b/q(r-p)+c/r(p-q)=0`
View Solution
SECTION - B questions and complete solutions for chapter REVISION PAPER -3 of SELINA MATHS (ENGLISH) of Class 10