Complete Solutions to QUESTIONS of chapter SECTION AND MID-POINT FORMULA of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SECTION AND MID-POINT FORMULA |
| SELINA PUBLICATION | QUESTIONS |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
Find the co-ordinates of point P which divides the line joining A (4,-5) and B (6,3) in the ratio 2 : 5.
View SolutionFind the ratio in which the point (5,4) divides the line joining points (2,1) and (7,6)
View SolutionIn what ratio is the joining the points (4,2) and (3,-5) divided by the x-axia ? Also, find the co-ordinates of the point of intersection.
View SolutionCalcuate the ratio in which the line joining the points (4,6) and (-5,4) is divided by the line y = 3. Also, find the co-ordinates of the point of intersection.
View SolutionThe origin O,B (-6,9) and C (12, -3) are vertices of triangle OBC, Point P divides OB in the ratio 1 : 2 and point Q divides OC in the ratio 1 : 2 Find the co-ordinates of points P and Q. Also show that `PQ = (1)/(3)` BC.
View SolutionFind the co-ordinates of the points of trisection of the segment joining the points A (6,-2) and (-8,10).

View SolutionShow that P (3,m -5) is a point of trisection of the line segment joining the points A (4,-2) and B (1, 4). Hence, find the value of 'm'.
View SolutionIf the point P(-1,2) divides the join of points A(2, 5) and B(a, b) in the ratio 3 : 4, find the value of `a xx b - a`.
View SolutionFind the co-ordinates of the mid point of the line segment joining the points P (4, -6) and (-2, 4).
View SolutionThe mid - point of line segment AB (shown in the diagram) is (-3, 5), Find the co-ordinates of A and B.
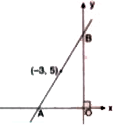 .
.
View SolutionPoints A(7, -4), B(-5, 5) and C(-3, 8) are vertices of triangle ABC, Find the length of its median through vertex A.
View SolutionA (14, -2), B(6, -2) and D (8,2) are the three vertices of a parallelgram ABCD. Find the co-ordinates of the fouth vertex C.
View SolutionThe mid-point of the segment joining (3m, 6) and (-4, 3n) is (1, 2m, -1). Find the values of m and n.
View SolutionThe point A(3, - 5) is reflected in the point P (-4, 3) as point A'. Find the co-ordinates of point A'.
View SolutionIf the mid-point of the segment joining the points A(3,4) and B(k,6) is (x,y) and x + y = 10, find the value of k and the length of the line segment AB.
View SolutionFind the co-ordinates of the point of intersection of the medians of triangle ABC, given A = (-2, 3), B = (6, 7) and C = (4,1).
View SolutionABC is a triangle and G (4, 3) is the centroid of the triangle. If A = (1, 3), B = (4, b) and C = (a, 1), find 'a' and 'b'.
Find the length of side BC.
View Solution
QUESTIONS questions and complete solutions for chapter SECTION AND MID-POINT FORMULA of SELINA MATHS (ENGLISH) of Class 10