Complete Solutions to EXERCISE 13 (C) of chapter SECTION AND MID-POINT FORMULA of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SECTION AND MID-POINT FORMULA |
| SELINA PUBLICATION | EXERCISE 13 (C) |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
Given a triangle ABC in which A = (4, -4) B = (0,5) and C = (5, 10). A point P lies on BC such that BP : PC = 3 : 2. Find the length of line segment AP.
View SolutionA(20, 0) and B (10, -20) are two fixed points. Find the co-ordinates of the point P in AB such that : 3PB = AB. Also , find the co-ordinates of some other Point Q in AB such that : AB = 6 AQ.
View SolutionA(-8, O), B(0, 16) and C(0, 0) are the vertices of a triangle ABC. Point P lies on AB and Q lies on AC such that AP : PB = 3 : 5 and AQ: QC = 3:5.
Show that : PQ = `(3)/(8)` BC.
View SolutionFind the co-ordinates of points of trisection of the line segment joining the point (6, -9) and the origin.
View SolutionA line segment joining `A (-1,(5)/(3))` and B(a, 5) is divided in the ratio 1: 3 at P, the point where the line segment AB intersects the y-axis.
Calculate the value of a'.
View SolutionA line segment joining `A (-1,(5)/(3))` and B(a, 5) is divided in the ratio 1: 3 at P, the point where the line segment AB intersects the y-axis.
Calculate the co-ordinates of 'P'.
View SolutionIn what ratio is the line joining A(0, 3) and B(4, -1) divided by the x-axis ?
Write the co-ordinates of the point where AB intersects the x-axis.
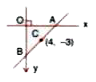
View SolutionThe mid-point of the A segment AB, as shown in diagram, is C (4, -3). (4, -3) Write down the co ordinates of A and B.
View SolutionAB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7). Find
the length of radius AC
View SolutionAB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7). Find
the coordinates of B.
View SolutionFind the co-ordinates of the centroid of a triangle ABC whose vertices are :
A(-1, 3), B(1, -1) and C(5, 1)
View SolutionThe mid-point of the line segment joining (4a, 23) and (-4, 3b) is (2, -2a). Find the values of a and b
View SolutionThe mid-point of the line segment joining (2a, 4) and (-2, 2b) is (1, 2a + 1). Find the values of a and b.
View SolutionWrite down the co-ordinates of the point P that divides the line joining A(-4, 1) and B(17, 10) in the ratio 1:2.
View Solutionwrite down the coordinate of the point p that divides the line joining A(-4,1) and B(17,10) in the ratio 1:2
Calculate the distance OP, where O is the origin.
View Solutionwrite down the coordinate of the point p that divides the line joining A(-4,1) and B(17,10) in the ratio 1:2
In what ratio does the y-axis divide the line AB ?
View SolutionProve that the points A(-5, 4), B(-1, -2) and C(5, 2) are the vertices of an isosceles rightangled triangle. Find the co ordinates of D so that ABCD is a square.
View SolutionM is the mid-point of the line segment joining the points A(-3, 7) and B(9, -1). Find the co-ordinates of point M. Further, if R(2, 2) divides the line segment joining M and the origin in the ratio p : q, find the ratio p : q.
View SolutionCalculate the ratio in which the line joining A (-4, 2) and B (3, 6) is divided by point P (x, 3). Also, find (i) x
View SolutionDetermine the ratio in which the line 2x +y 4 = 0 divides the line segment joining the points A(2, 2) and B(3,7).
View SolutionIf the abscissa of a point P is 2, find the ratio in which this point divides the line segment joining the points (-4, 3) and (6,3). Also, find the co-ordinates of point P.
View SolutionThe line joining the points (2, 1) and (5, -8) is trisected at the points P and Q. If point P lies on the line 2x - y + k = 0, find the value of k. Also, find the co-ordinates of point Q.
View SolutionFind the image of the point A(5, -3) under reflection in the point P(-1, 3).
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
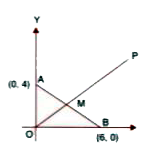
co-ordinates of M
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
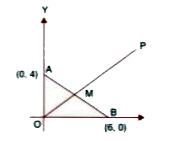
co-ordinates of P
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
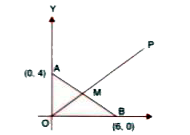
length of BP
View SolutionA (-4, 2), B(0, 2) and C(-2,-4) are vertices of a triangle ABC. P, Q and R are mid-points of sides BC, CA and AB respectively. Show that the centroid of `Delta` PQR is the same as the centroid of `Delta` ABC.
View SolutionA(3, 1), B(y, 4) and C(1, x) are vertices of triangle ABC and G(3, 4) is its centroid. Find the values of x and y. Also, find the length of side BC.
View Solution
EXERCISE 13 (C) questions and complete solutions for chapter SECTION AND MID-POINT FORMULA of SELINA MATHS (ENGLISH) of Class 10