Complete Solutions to EXERCISE 13 (B) of chapter SECTION AND MID-POINT FORMULA of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SECTION AND MID-POINT FORMULA |
| SELINA PUBLICATION | EXERCISE 13 (B) |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
Find the mid-point of the line segment joining the points :
(-6, 7) and (3, 5)
View SolutionFind the mid-point of the line segment joining the points :
(5, -3) and (-1, 7)
View SolutionPoints A and B have co-ordinates (3, 5) and (x, y) respectively. The mid-point of AB is (2, 3). Find the values of x and y.
View SolutionA (5, 3), B (-1, 1) and C (7, -3) are the vertices of triangle ABC. If L is the mid-point of AB and M is the mid-point of AC, show
that : `LM = (1)/(2) BC`.
View SolutionGiven M is the mid-point of AB, find the co-ordinates of:
A, if M = (1, 7) and B = (-5, 10),
View SolutionGiven M is the mid-point of AB, find the co-ordinates of:
B, if A = (3,-1) and M = (-1, 3).
View SolutionP (-3, 2) is the mid point of line segment AB as shown in the given figure. Find the P (-3,2) co-ordinates of points A and B.
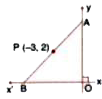
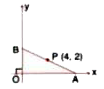
View SolutionIn the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
View Solution(-5, 2), (3, -6) and (7, 4) are the vertices of a triangle. Find the length of its median through the vertex (3,-6).
View SolutionGiven a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.
View SolutionOne end of the diameter of a circle is (-2, 5). Find the co-ordinates of the other end of it, if the centre of the circle is (2, -1).
View SolutionA (2, 5), B (1, 0), C (-4, 3) and D (-3, 8) are the vertices of quadrilateral ABCD. Find the co-ordinates of the mid-points of AC and BD. Give a special name to the quadrilateral.
View SolutionP (4, 2) and Q (-1, 5) are the vertices of parallelogram PQRS and (-3, 2) are the co-ordinates of the point of intersection of its diagonals. Find co-ordinates of R and S.
View SolutionA (-1, 0), B (1, 3) and D (3, 5) are the vertices of a parallelogram ABCD. Find the co-ordinates of vertex C.
View SolutionThe points (2, -1), (-1, 4) and (-2, 2) are mid-points of the sides of a triangle. Find its vertices.
View SolutionPoints A (-5, x), B (y, 7) and C (1, -3) are collinear (i.e. lie on the same straight line) such that AB = BC. Calculate the values of x and y.
View SolutionPoints P (a, -4), Q (-2, b) and R (0, 2) are collinear. If lies between P and R, such that PR = 2QR, calculate the values of a and b.
View SolutionCalculate the co-ordinates of the centroid of the triangle ABC, if A = (7, -2), B = (0, 1) and C = (-1, 4).
View Solutionhe co-ordinates of the centroid of a triangle PQR are (2, -5). If Q = (-6, 5) and R = (11, 8), calculate the co-ordinates of vertex P.
View SolutionA (5, x), B (-4, 3) and C (y, -2) are the vertices of the triangle ABC whose centroid is the origin. Calculate the values of x and y.
View Solution
EXERCISE 13 (B) questions and complete solutions for chapter SECTION AND MID-POINT FORMULA of SELINA MATHS (ENGLISH) of Class 10