Complete Solutions to Exercise 6a of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| NAGEEN PRAKASHAN | Exercise 6a |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
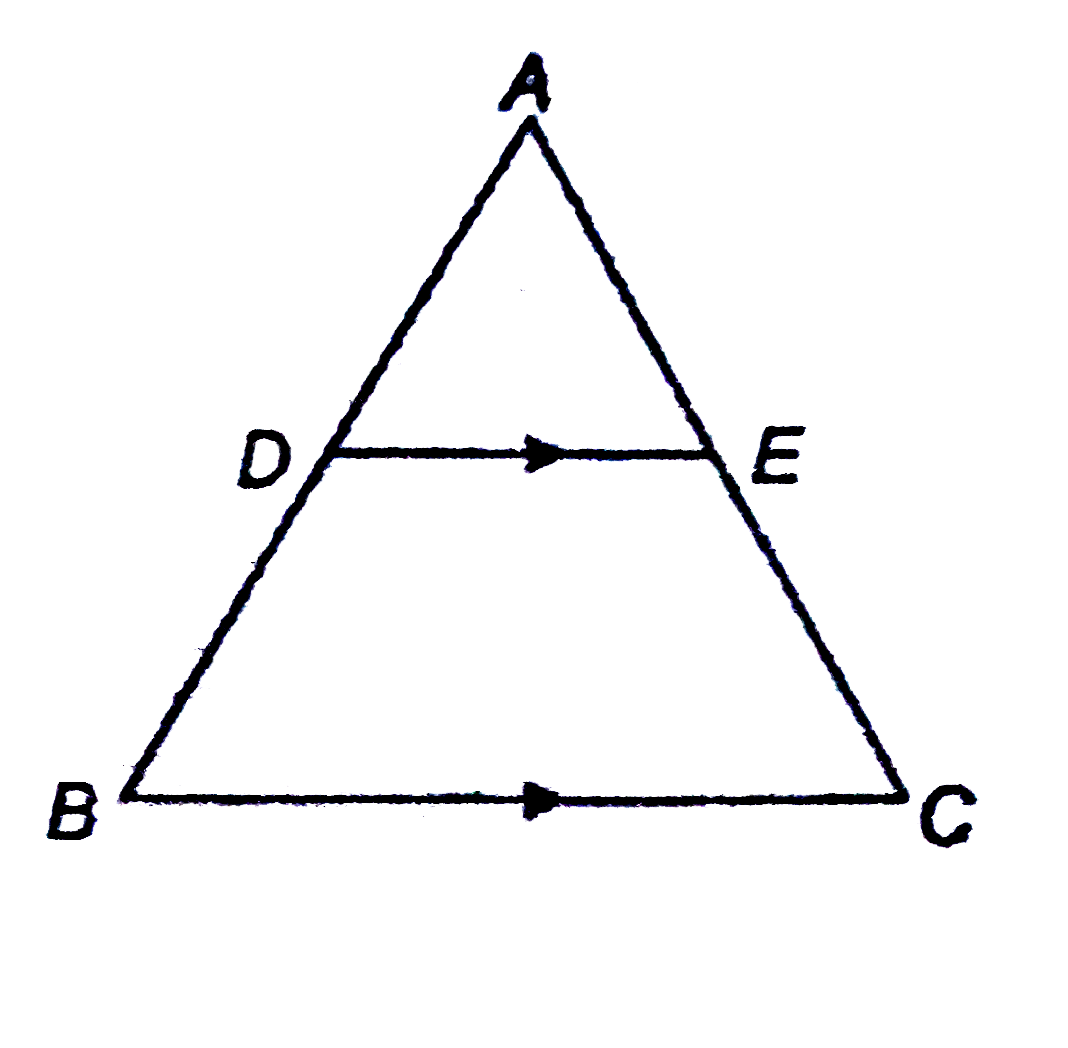
In the adjoining figure DE||BE and D divides AB in the ratio 2:3 find.
(i) `(AE)/(EC)` (ii) `(AE)/(AC)`
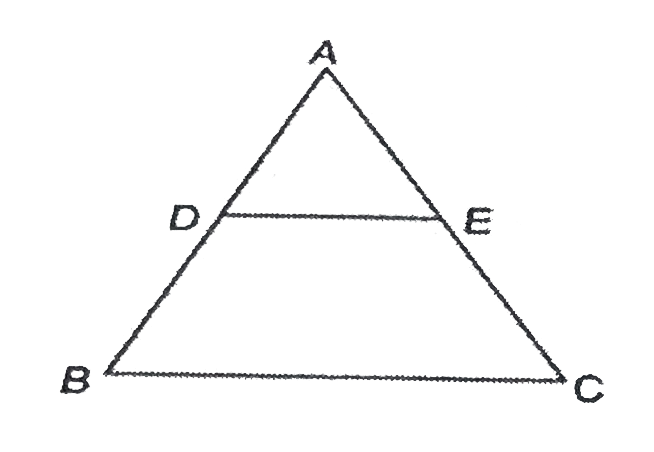
View SolutionIn the figure DE is parallel to BC and `(AD)/(DB) = 2/3` if AE = 3.7 cm find EC.
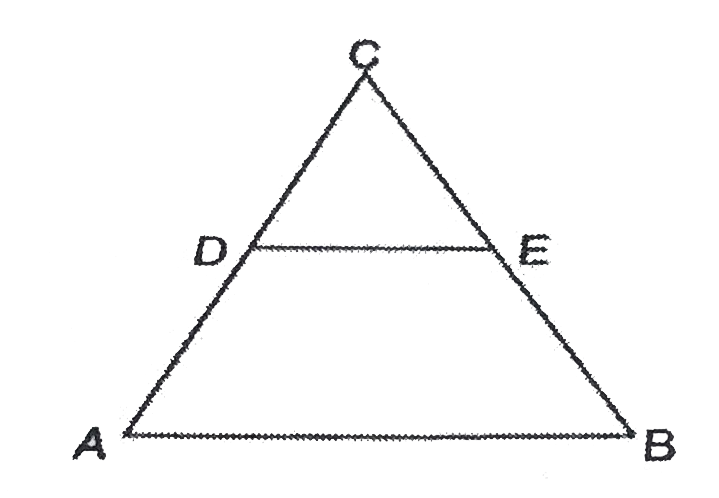
View SolutionIn the figure if DE||AB, find the value of x . Given AD= (x-4).
DC= 4cm, EB= (3x-19) cm and EC= (x-3) cm.
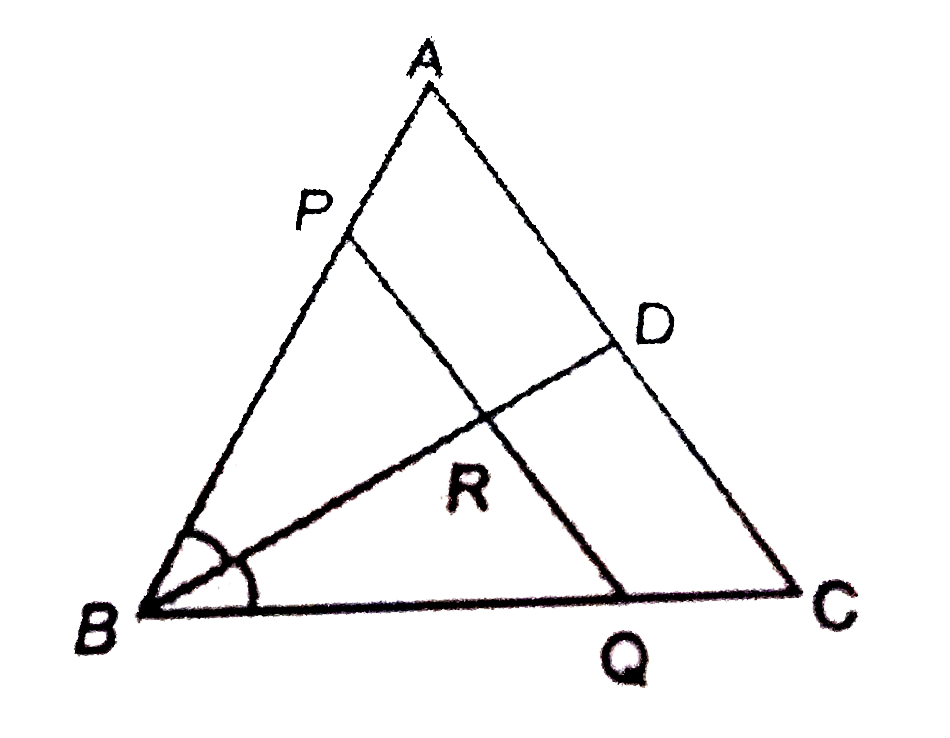
View SolutionIn the given figure if PQ||YZ. Find XQ.

View Solution`Da n dE` are respectively the points on the side `A Ba n dA C` of a ` A B C` such that `A B=5. 6 c m ,A D=1. 4 c m ,A C=7. 2 c m` and `A E=1. 8 c m ,` show that `D E B Cdot`
View SolutionIn a ` A B C` , `D` and `E` are points on the sides `A B` and `A C` respectively such that `D E B C` If `A D=6\ c m` , `D B=9\ c m` and `A E=8\ c m` , find `A C` . (ii) If `(A D)/(D B)=3/4` and `A C=15\ c m` , find `A E` . (iii) If `(A D)/(D B)=2/3` and `A C=18\ c m` , find `A E` .
View SolutionIn Fig. 4.20, if `P Q B C` and `P R C D` . Prove that (i) `(A R)/(A D)=(A Q)/(A B)` (ii) `(Q B)/(A Q)=(D R)/(A R)` . (FIGURE)
View SolutionIn a ` A B C ,D` and `E` are points on sides `A Ba n dA C` respectively such that `B D=C Edot` If `/_B=/_C ,` show that `D E B Cdot`
View SolutionIn ` A B C ,\ D` and `E` are points on sides `A B` and `A C` respectively such that `A DxxE C=A ExxD B` . Prove that `D E B C` .
View SolutionIn the given figure, if DE||AQ and DF||AR. Prove that EF||QR.

View SolutionIn the given figure A, B and C are points on OP, OQ and OR respectively such that AB||PQ and BC||QR. Show that AC||PR.

View SolutionProve that the diagonals of a trapezium divide each other proportionally.
View SolutionIn `triangleABC`the bisector of `angleB` meets AC at D. A line PQ||AC meets AB,BC and BD at P, Q and R respectively.
show that `PRxxBQ = QRxxBP`.
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at the point O such that `(A O)/(B O)=(C O)/(D O)`. Show that ABCD is a trapezium.
View SolutionIn the given figure AD is the bisector of `angleA`. If BD= 4 cm , DC = 3 cm and AB = 6cm . Find AC.

View SolutionThe bisector of interior `/_A` of ` A B C` meets `B C` in `D ,` and the bisector of exterior `/_A` meets `B C` produced in `Edot` Prove that `(B D)/(B E)=(C D)/(C E)dot`
View Solution`A D` is a median of ` A B C` . The bisector of `/_A D B` and `/_A D C` meet `A Ba n dA C` in `Ea n dF` respectively. Prove that `E F B Cdot`
View SolutionIf the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
View SolutionD,E and F are the points on sides BC, CA and AB respectively, of `triangleABC` such that AD bisects `angleA`, BE bisects `angleB` and CF bisects `angleC`. If AB=5 cm, BC= 8cm and CA= 4 cm. find AF, CE and BD.
View SolutionIf the diagonal BD of a quadrillateral ABCD bisects both `angleB and angleD`. Prove that `(AB)/(BC)= (AD)/(CD)`.
View SolutionProve that the line segments joints joining the mid-points of the adjacent sides of a quadrilateral from a parallelogram.
View SolutionIn figure, `P` is the mid-point of `B C ,Q` is the mid-point of `B C ,Q` is the mid-point of `A P` , such that `B Q` produced meets `A C` at `Rdot`
View SolutionIn `A B C D` is a parallelogram in which `P` is the mid-point of `D C` and `Q` is a point on `A C` such that `C Q=1/4A Cdot` If `P Q` produced meets `B C` at `Rdot` Prove that `R` is a mid-point of `B Cdot`
View Solution
Exercise 6a questions and complete solutions for chapter TRIANGLES of NAGEEN MATHS (HINGLISH) of Class 10