Complete Solutions to Exercise 6d of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| NAGEEN PRAKASHAN | Exercise 6d |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
Find in each cash whether the sides of the triangle,as given below form a right triangle or not
(1) 9 cm, 12 cm and 15 cm (ii) 8 cm ,15 cm and 17 cm
(iii) 7 cm, 24 cm and 25 cm
View SolutionIn `triangleABC` right angled at C
( i) AB= 1.7 cm, BC= 1.5 cm, find CA (ii) CA=2.4 cm, AB = 4.0 cm, find BC
View SolutionA ladder reachs a window which is 15 metres above the ground on one side of the steet. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 8 metres high. Find the width of the street, if the ladder is 13 meters.
View SolutionA man goes 40m due north and then 50m due west. Find his distance from the starting point.
View SolutionThe side of a rhombus is 13 cm. if one if the diagonals is 24 cm, find the length of the other diagonal.
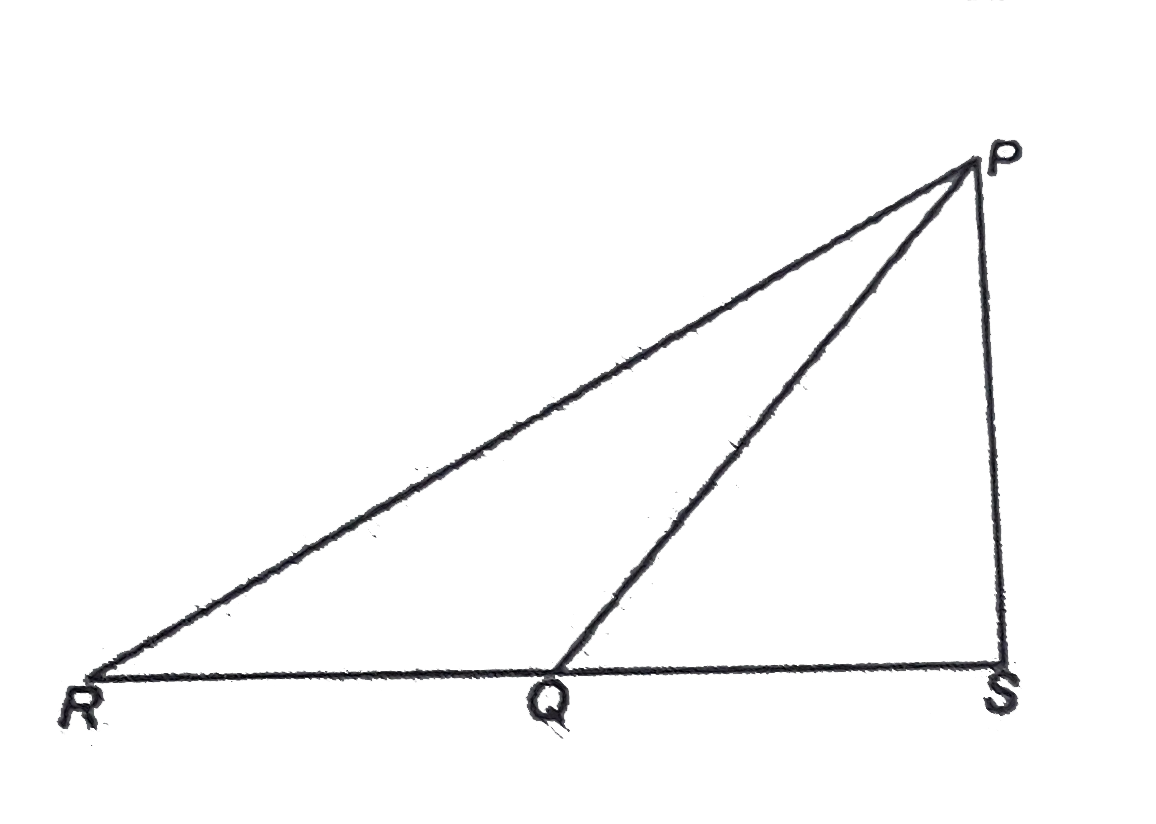
View SolutionIn the adjoining figure: `anglePSQ= 90^(@)` , PQ= 10 cm , QS = 6cm and RQ = 9cm . Calculate the length of PR.
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that ` AB^(2) = 2AC^(2)`
View Solution`triangleABC` is an isosceles triangle with AC = BC. If `AB^(2)= 2AC^(2)` . Prove that ` triangle ABC` is a right triangle.
View SolutionIn an equilateral `triangleABC, AD` is the altitude drawn from A on the side BC. Prove that `3AB^(2) = 4AD^(2)`
View SolutionM and N are the points on sides QR and PQ respectively of a `trianglePQR`, right angled at Q. prove that ` PM^(2) + RN^(2)= PR^(2)+MN^(2)`
View SolutionIn a square ABCD, show that `AC^(2) = 2AB^(2)`.
View SolutionIn a rhombus ABCD, prove that `AC^(2) + BD^(2) = 4AB^(2)`
View SolutionIn triangle ABC, `angleA = 90^(@)` , CA= AB and D is a point on AB porduced. Prove that :
` DC^(2) - BD^(2) = 2AB. AD`
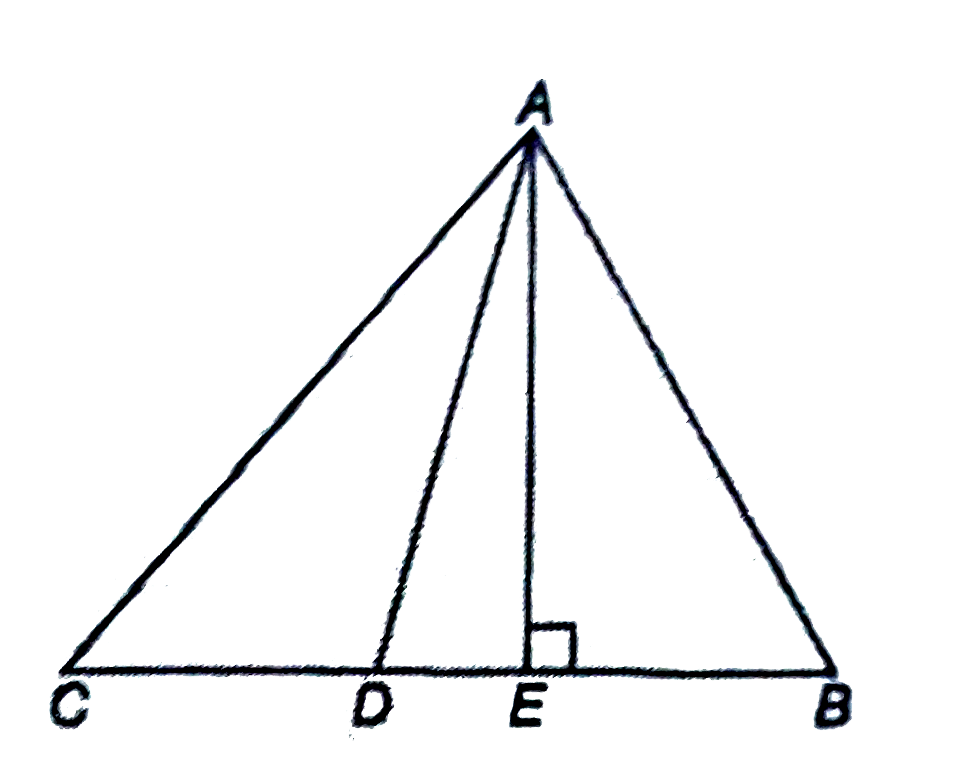
View SolutionThe following figure shows a triangle ABC in which AD is a median and ` AE bot BC`. Prove that ` 2AB^(2)+ 2AC^(2) = 4AD^(2) + BC^(2)` .
View SolutionFrom a point `O` in the interior of a ` A B C` , perpendiculars `O D ,\ O E` and `O F` are drawn to the sides `B C ,\ C A` and `A B` respectively. Prove that: (i) `A F^2+B D^2+C E^2=O A^2+O B^2+O C^2-O D^2-O E^2-O F^2` (ii) `A F^2+B D^2+C E^2=A E^2+C D^2+B F^2`
View SolutionIn a right triangle ABC, right angled at A, AD is drawn perpendicular to BC. Prove that:
` AB^(2)-BD^(2)= AC^(2)-CD^(2)`
View SolutionIn the given figure , ABC is a right triangle, right angled at B. Medians AD and CE are of respective length 5 cm and `2sqrt5 cm` . Find the length of AC.

View SolutionIn the given figure , `angleQPR= 90^(@)` QR = 26 cm PM = 6cm, MR = 8cm and `anglePMR= 90^(@)` . Find the area of triangle PQR.

View SolutionGiven a right angled `triangleABC`. The lengths of the sides containing the right angle are 6 cm and 8 cm. A circule is inscribed in `triangleABC`. Find th radius of the circle.
View SolutionIn an acute angled triangle , express a median in term of its sides.
View SolutionIn a quadrilateral ABCD, `angleB=90^(@) and AD^(2)= AB^(2) + BC^(2)+CD^(2)` prove that ` angleACD= 90^(@)` .
View SolutionABC is a right triangle right angled at C and AC = ` sqrt3BC` . Prove that ` angleABC= 60^(@)` .
View SolutionIn `triangleABC , angleA= 60^(@)` prove that `BC^(2)= AB^(2)+AC^(2)- AB . AC`
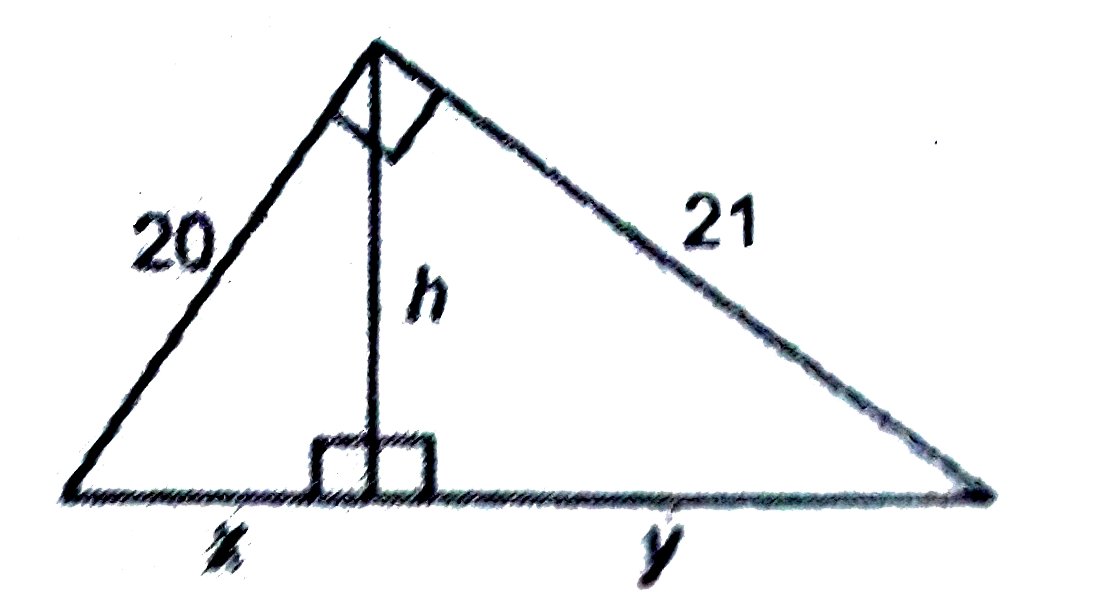
View SolutionIn the adjoining figure, find x,y and h.
View Solution
Exercise 6d questions and complete solutions for chapter TRIANGLES of NAGEEN MATHS (HINGLISH) of Class 10