Complete Solutions to Solved Example of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| NAGEEN PRAKASHAN | Solved Example |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
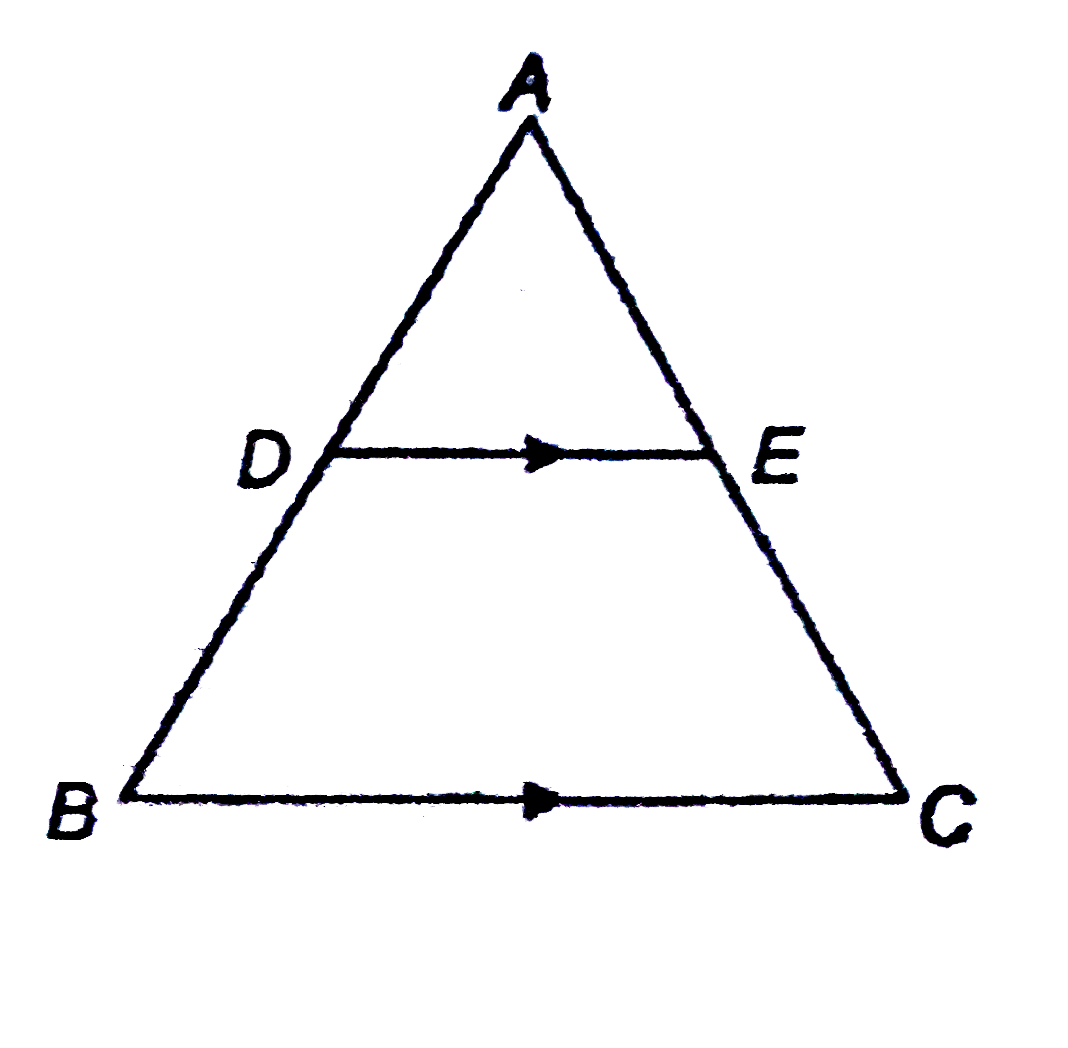
In the adjoining figure DE||BE and D divides AB in the ratio 2:3 find.
(i) `(AE)/(EC)` (ii) `(AE)/(AC)`
View SolutionIn the figure PQ is parallel to MN if `(KP)/(PM)= 4/13 and KN=2.4`.
Find KQ.

View Solutionif D and E are points on the sides AB and AC of a `DeltaABC`. Such that AB=12 cm, AD=8 cm, AE=12 cm, AC= 18 cm. show that DE||BC.
View SolutionIn the given figure, in `DeltaABC , DE||BC` so that `AD= (4x - 3) cm , AE= ( 8x-7) cm , BD= (3x-1) cm and CE= (5x-3) cm` . Find the value of x.
View SolutionIn `DeltaABC,D` and E are points on the sides AB and AC respectively. Find whether DE||BC if
(i) AD= 3cm , BD = 4.5cm, AE = 4cm, AC= 10cm
(ii) AB=7 cm , BD = 4.5cm, AE = 3.5 cm, CE= 5.6cm.
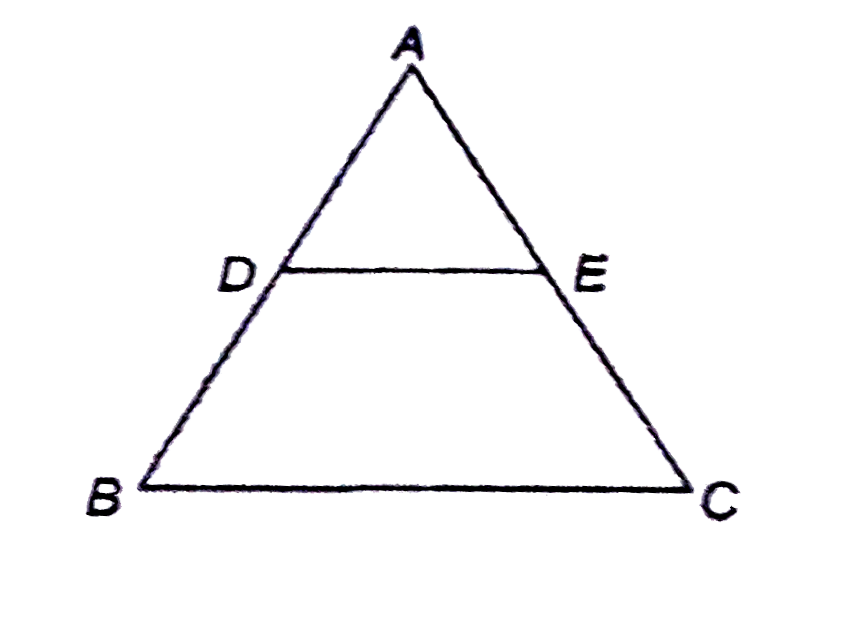
View SolutionIn the following figure AB||CD||EF||GH and BH=100 cm. find x and y.
View SolutionProve using similar triangles, that a line drawn through the mid-point of one side of a triangle parallel to another side, bisects the third side.

View SolutionProve that the line joining the mid-points of the two sides of a triangle is parallel to the third side.
View SolutionThe external angle bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle.
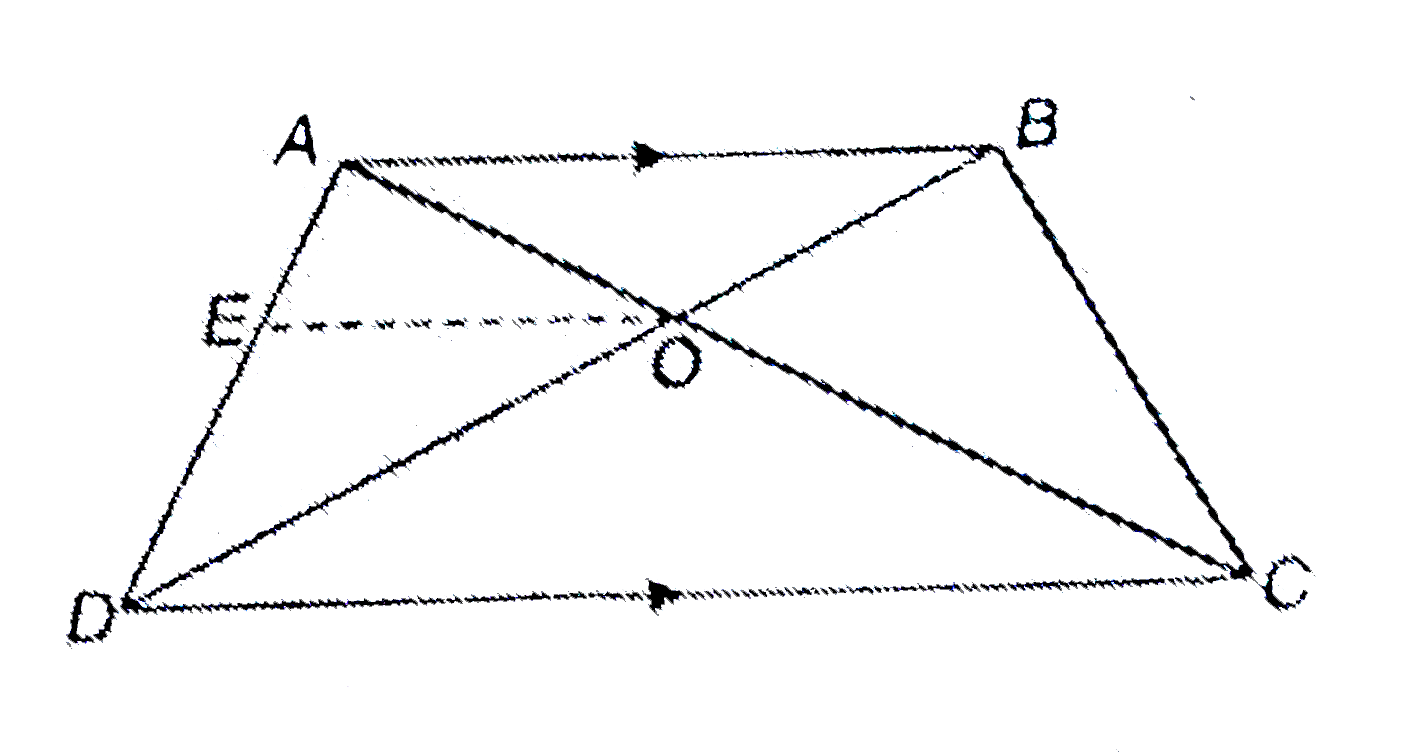
View SolutionABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that ` (AO)/(OC) = (BO)/(OD)`
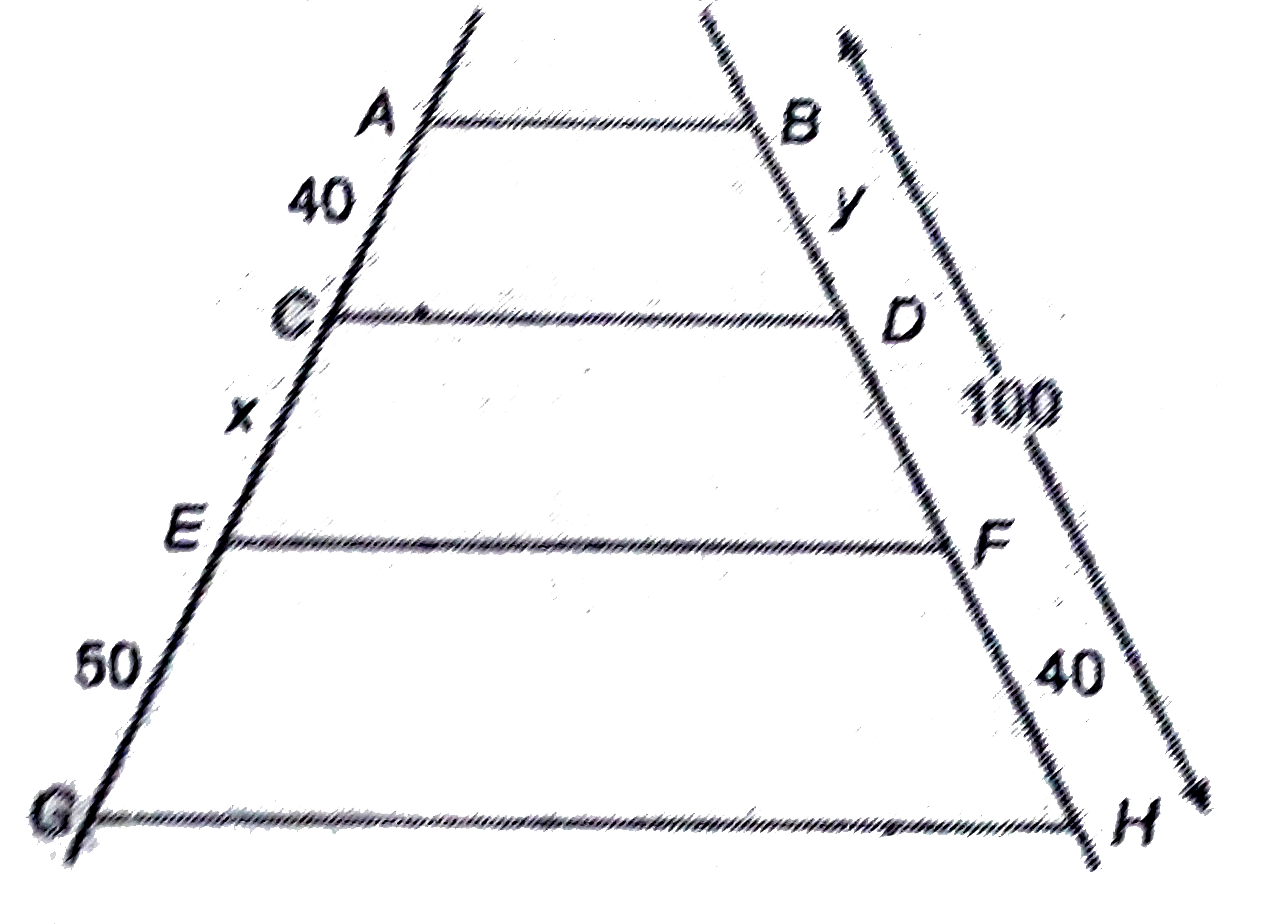
View SolutionAny line parallel to the parallel sides of a trapezium divides the non-parallel sides proportionally.

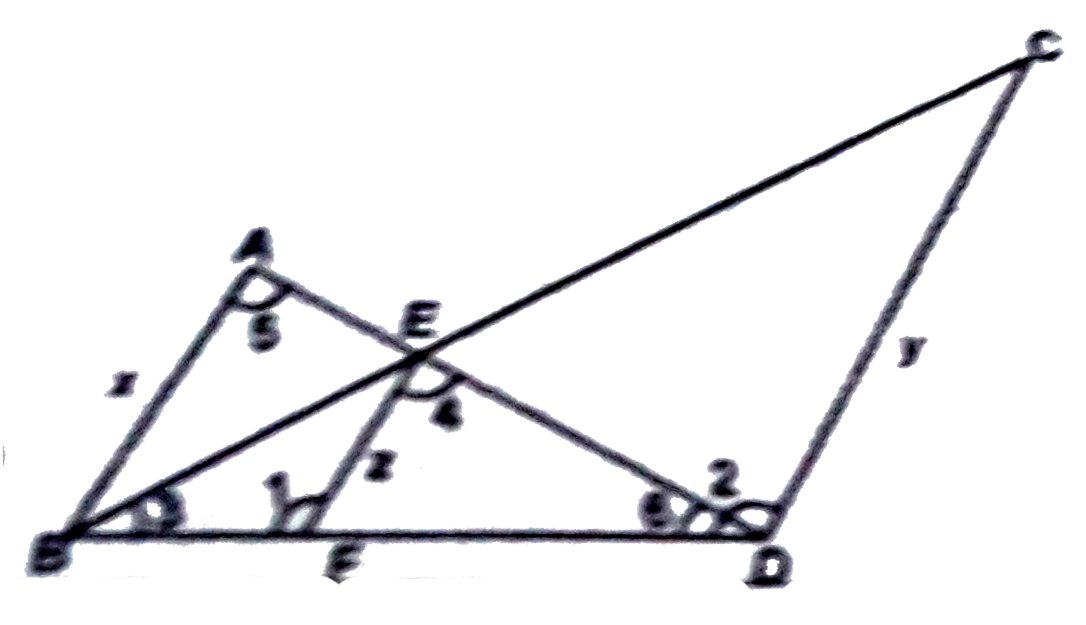
View SolutionThe side `B C` of a triangle `A B C` is bisected at `D ;o` is any point in `A D ,B Oa n dC O` produced meet `A Ca n dA B` in `Ea n dF` respectively and `A D` is produced to `X` so that `D` is the mid-point of `O Xdot` Prove that `A O : A X=A F : A B` and show that `F E B Cdot`
View SolutionLet `A B C` be a triangle and `Da n dE` be two points on side `A B` such that `A D=B Edot` If `D P || B C` and `E Q || A C ,` THEN PROVE THAT `P Q || A B`
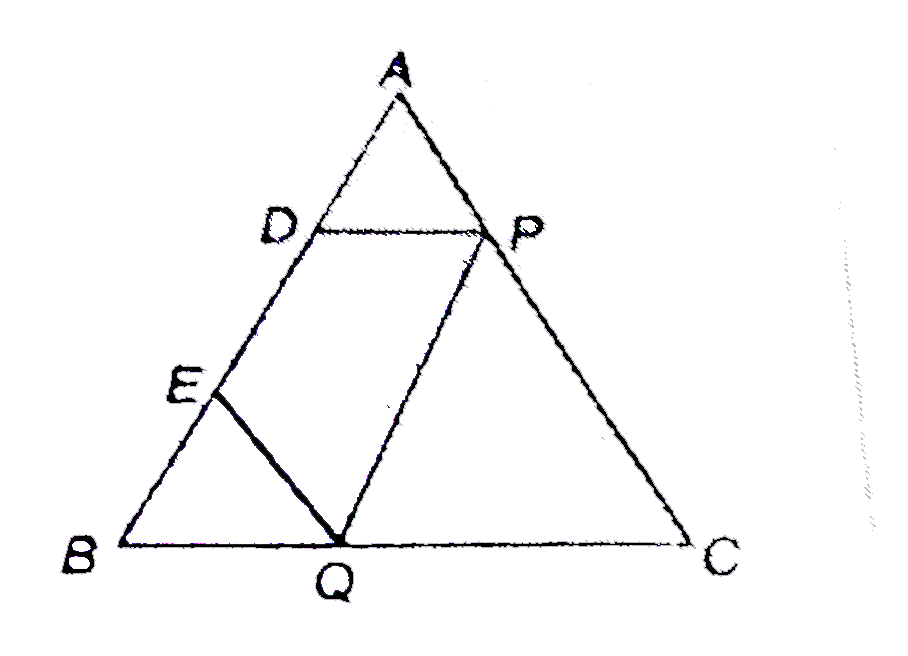
View SolutionIn figure, `DE || AB and BD || BEF.` Prove that `DC^2=CF xx AC`
View SolutionIn the given figure `triangleACB ~ triangleAPQ`. If BC= 8cm , PQ = 4cm BA= 6.5 cm, AP = 2.8 cm, find CA and AQ.
View SolutionThe triangles shown in adjoining figures are similar. Find the values of a and b.

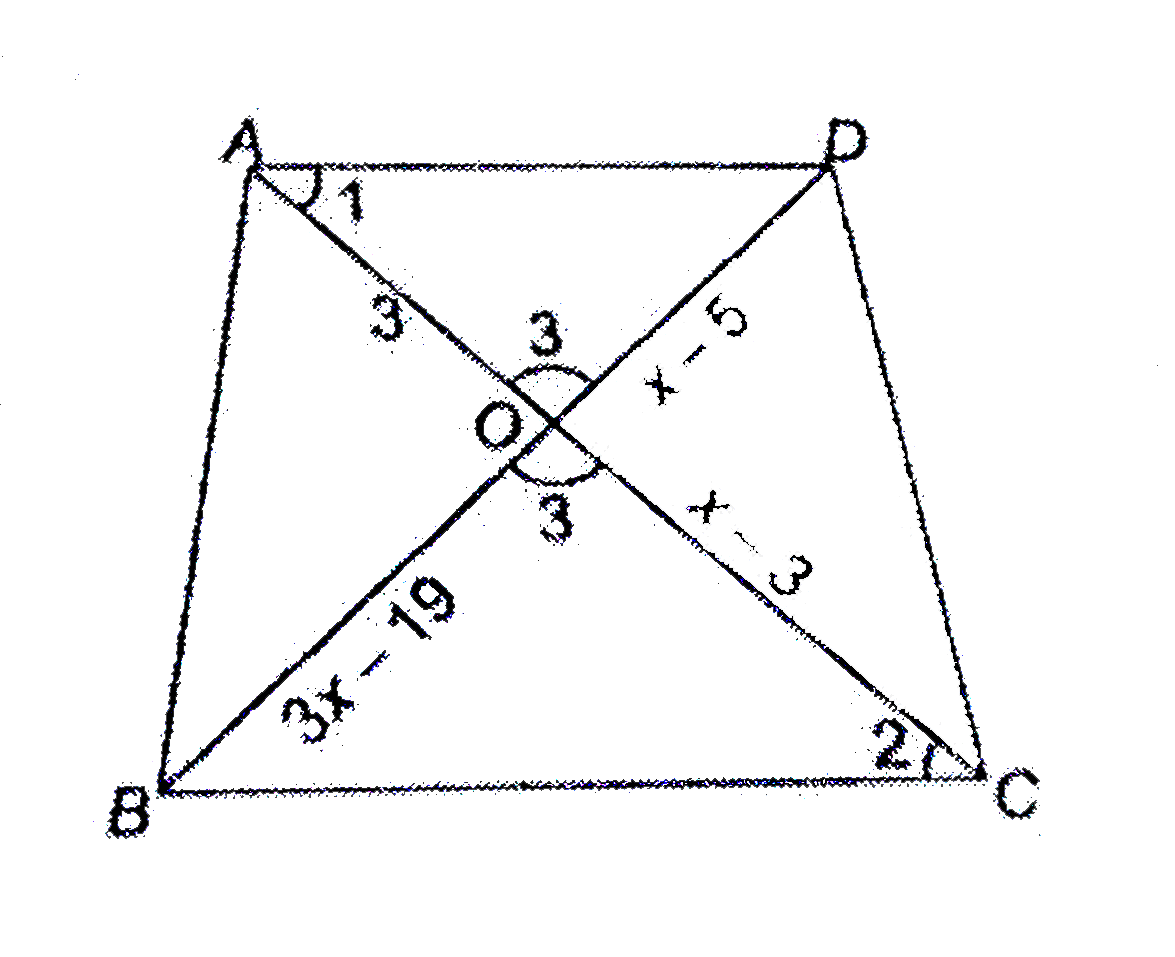
View SolutionIn the given figure if AD||BC, find the value of x.
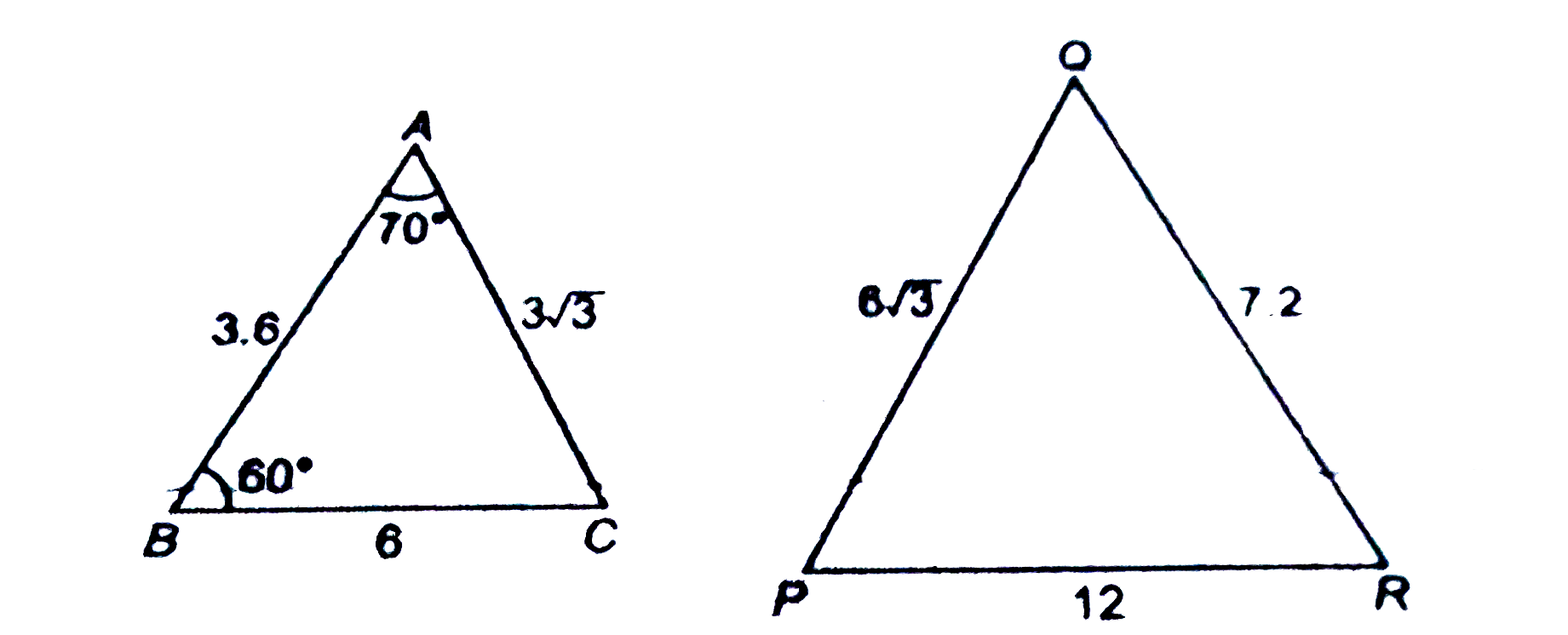
View SolutionFind `angleP` in the figure below.
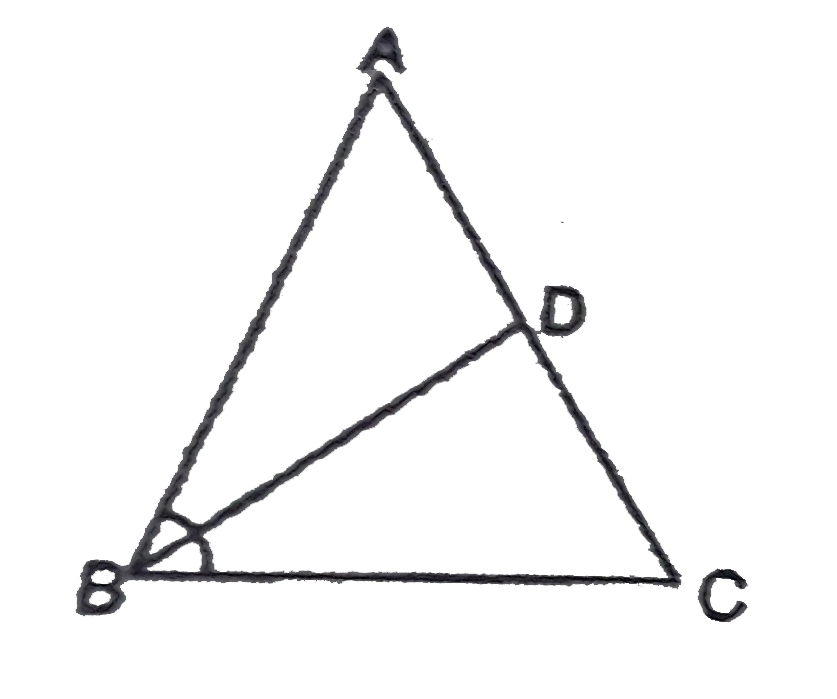
View SolutionIn the figure AC||BD , prove that:
`(i) triangleACE ~ triangleBDE (ii) (AE)/(CE)= (BE)/(DE)`

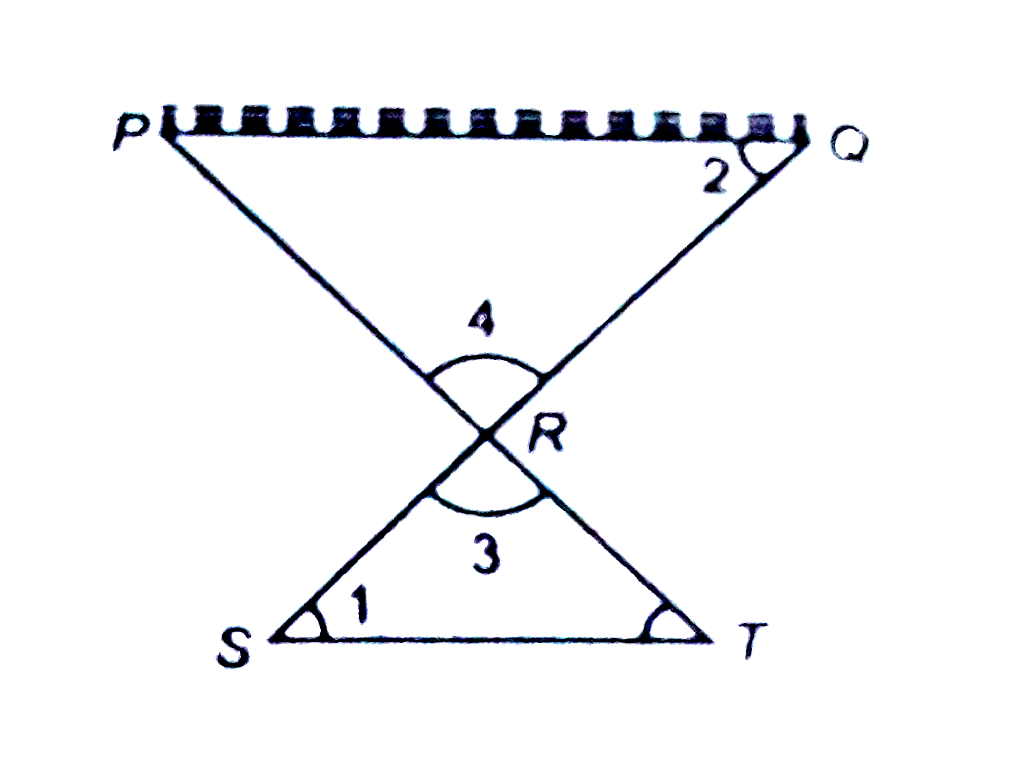
View SolutionS and T are points on sides PR and QR of ` Delta PQR ` such that `/_ P = /_ RTS` then
View Solution`A B C` is an isosceles triangle with `A B=A C` and `D` is a point on `A C` such that `B C^2=A CxxC Ddot` Prove that `B D=B C`
View SolutionIn the given figure if ` angleB= 90^(@)` and BD is perpendicular to AC then
prove that:
`(i) triangleADB~triangleBDC (ii) triangleADB~triangleABC`
(iii) `triangleBDC ~ triangleABC (iv) BD^(2)= AD xx DC`
(v) `AB^(2)= AD xx AC (vi) BC^(2)= CD xx AC`
(vii) `AB^(2)+BC^(2)= AC^(2)`

View SolutionIn the given figure , DEFG is a square and `angleBAC= 90^(@)` prove that (i) `triangleAGF~ triangleDBG` `(ii) triangleAGF~triangleEFC`
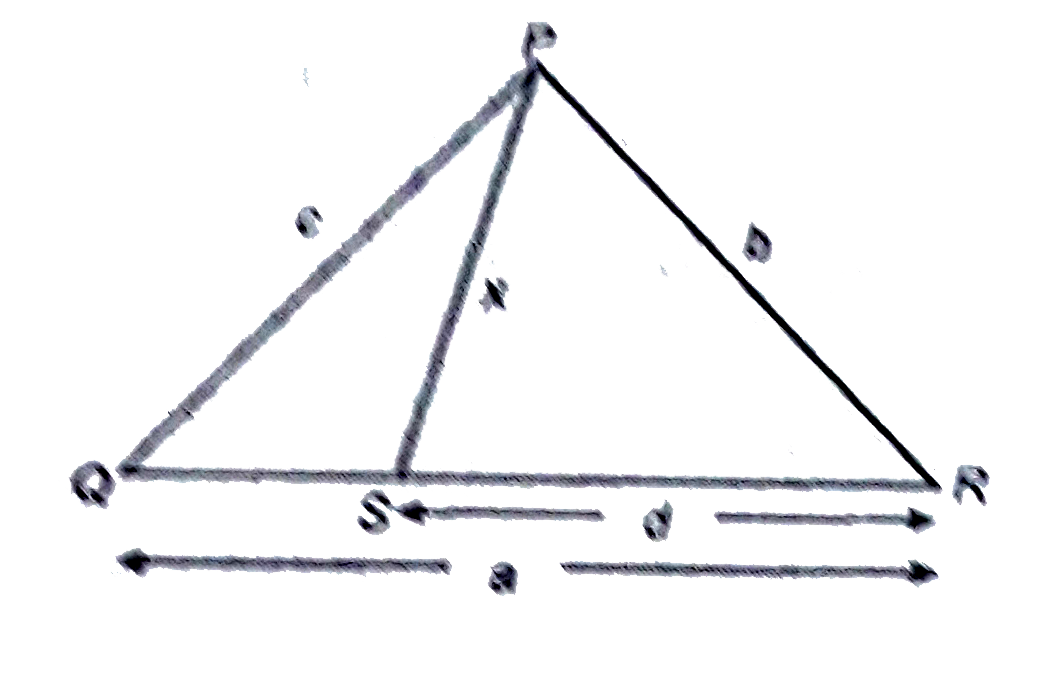
View SolutionIn the adjoining figure if a= 18 , b= 12,c = 14 and d=8 , what is the measure of x?
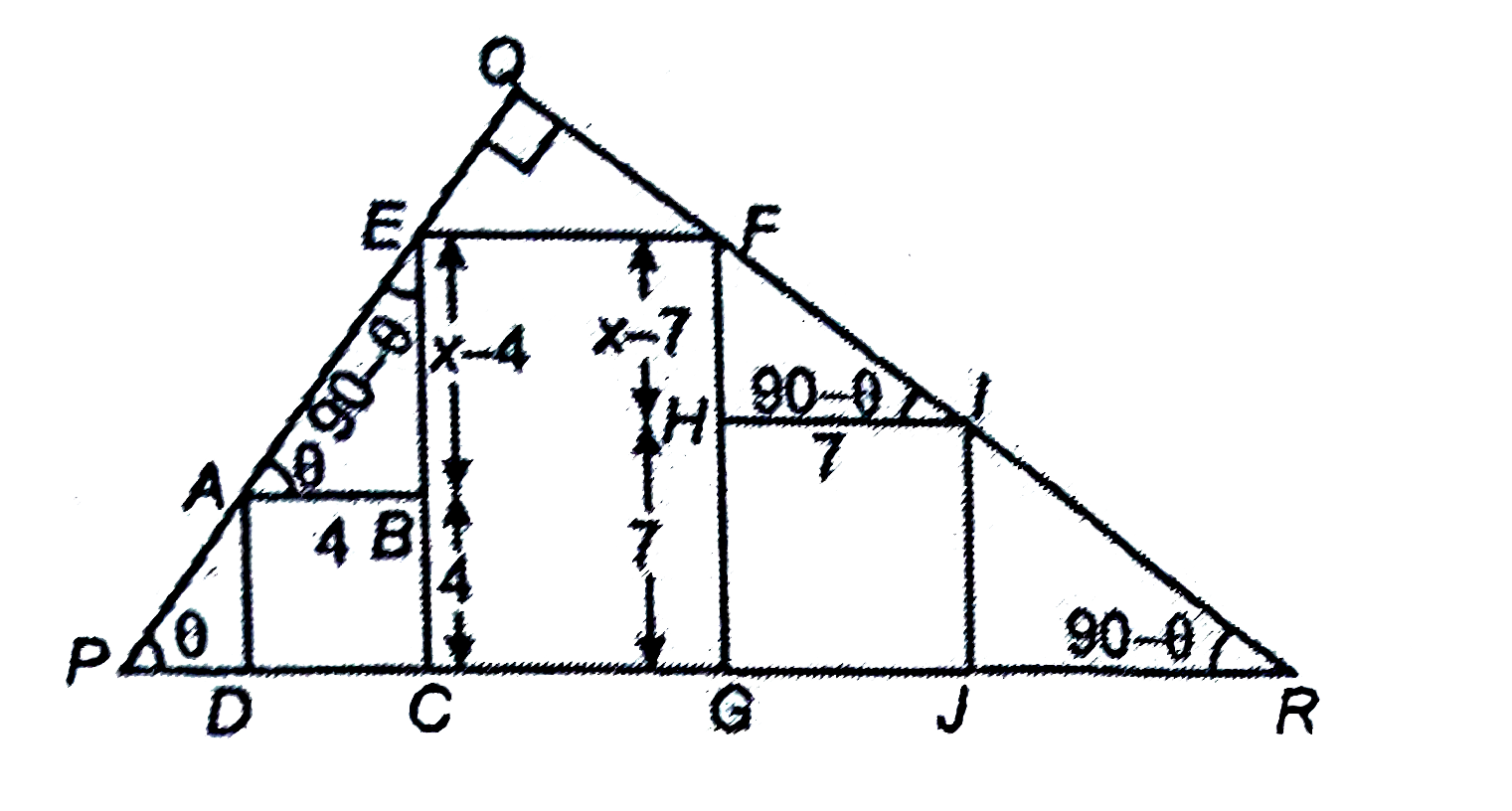
View SolutionIn the adjoining frigure , `trianglePQR` is a right angled triangle in which `anglePQR=90^(@), squreABCD` is a square of side 4 units and `squre GHIJ` is a square of side 7 units. EC and CG are the length and breadth of rectangle CEFG. Find the length EC.
View SolutionDr. Bansal needs to determine the distance PQ across a river in and east-west direction as shown in the adjoining figure. He can't measure this distance directly over the water. So, he selects the point S from where a straight line to point Q stays on land so he can mesure distance. he then moves eastward a distance of 400 m from point S to T , so that the line of sight from point T to P cuts the previous line SQ at R. finally with a long measuring tape. he determines that.
SR = 250 m, QR= 1250 m
Determine if this is enough information to calculate the distance PQ and if so, find PQ and hence find the time taken by a swimmer to cross the river PQ with a uniform speed of 800 m/hr.
View SolutionIn the adjoining figure , AB||CD||EF.
prove that `1/x+1/y=1/z`.
View SolutionIn trapezium ABCD. AB||DC and DC = 2AB. A line segment EF drawn parallel to AB cuts AD in F and BC in E such that `(BE)/(EC)=3/4` .
Diagonal DB intersects EF at G. prove that &EF= 10AB.
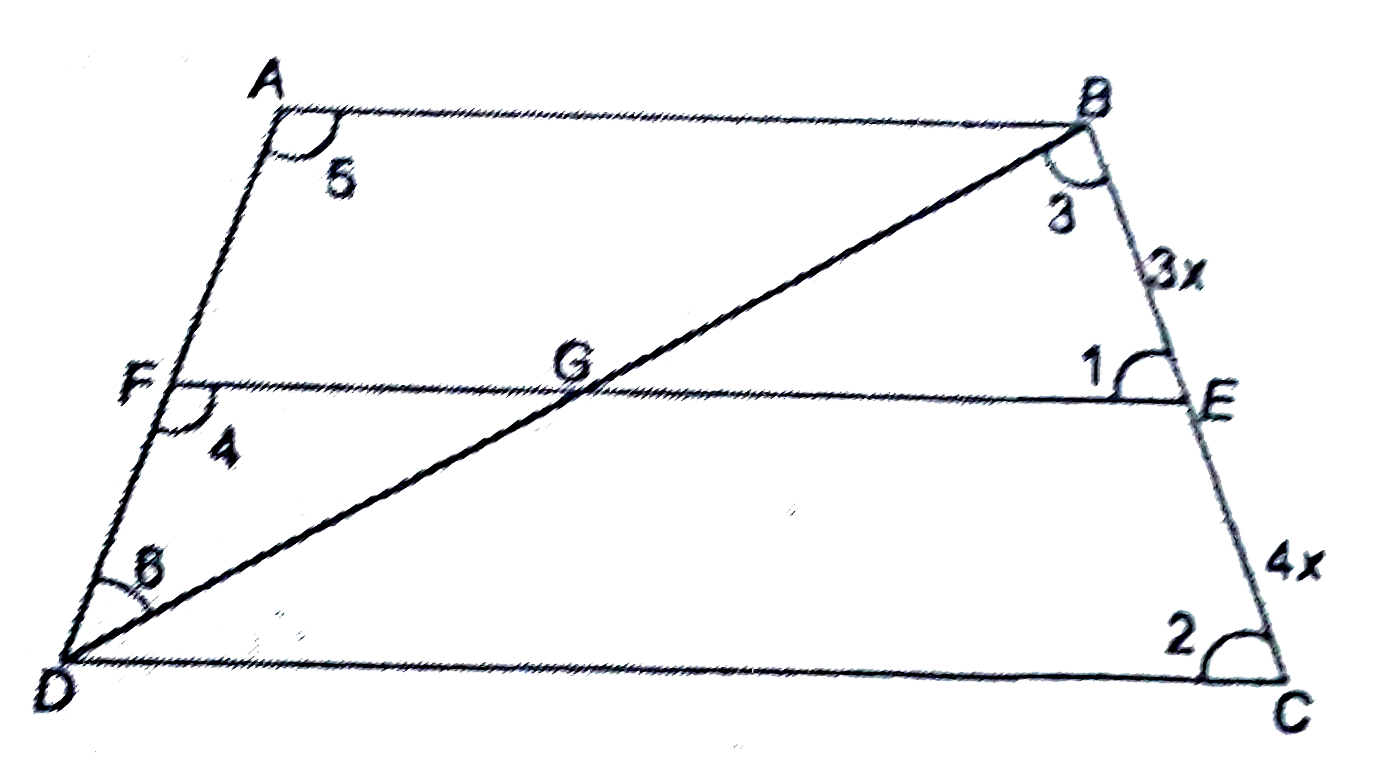
View SolutionThrough the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn, intersecting AC in L and AD produced in El. Prove that EL= 2BL
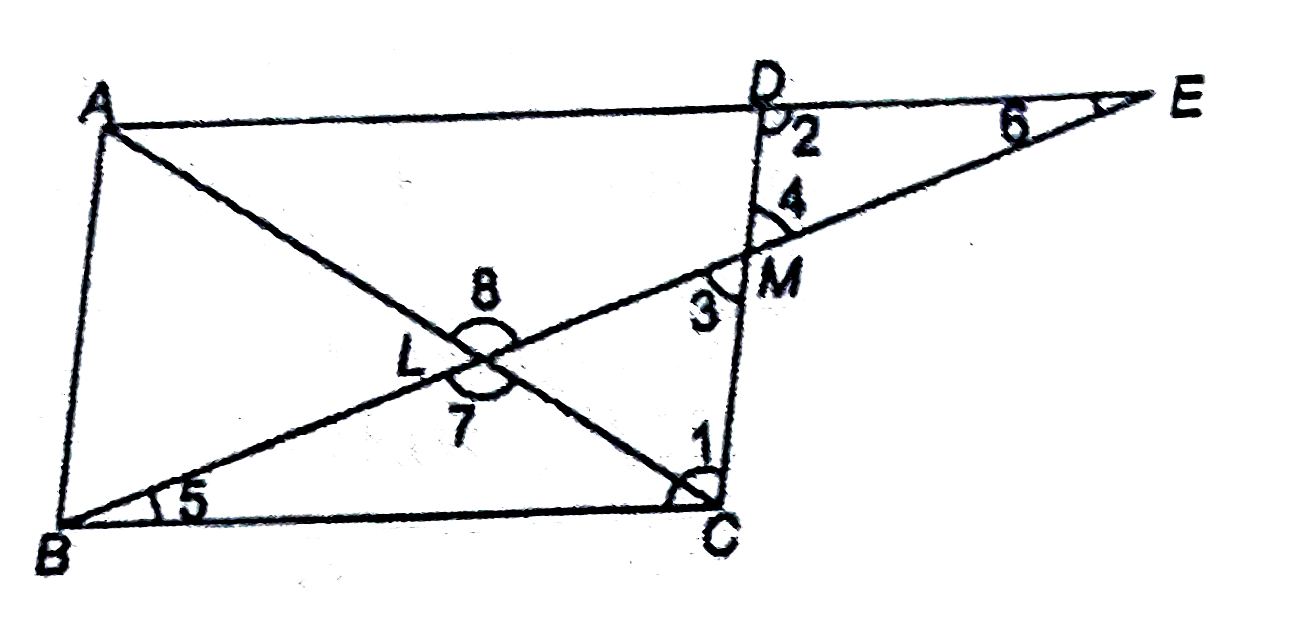
View SolutionIf two sides and a median bisecting one of these sides of a triangle are respectively proportional to the two sides and corresponding median of another triangle; then triangle are similar.
View SolutionIf two sides and a median bisecting the third side of a triangle ar respectively proportional to the corresponding sides and median of the other triangle; then the two triangles are similar.
View SolutionThe perimeters of two similar triangles are `25`cm and `15`cm respectively. If one side of first triangle is `9`cm, what is the corresponding side of the other triangle?
View SolutionA lamp is 3.3 m be the lamp post and CD= 110 cm tall walks away from the base of this lamp post at a speed of 0.8 m/s. find the length of the shadow of boy after 4 seconds.
View SolutionIn figures `triangle ABC and triangleDEF` ar similar , the areas of `triangle ABC` is 9 sq. m and that of `triangleDEF` is 16 sq. cm. if EF= 4.2 cm, find BC.
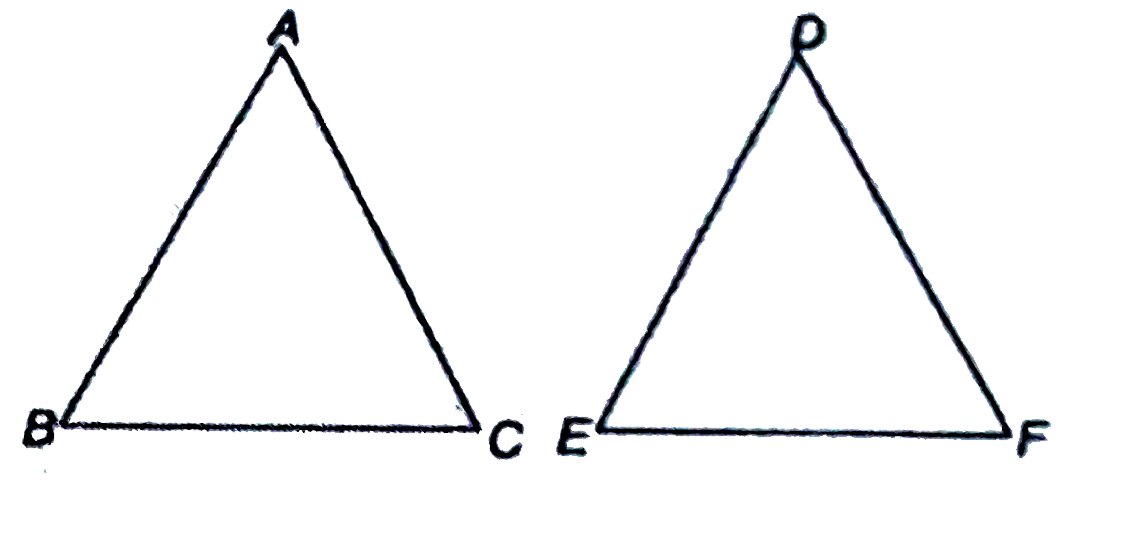
View SolutionIf D,E,F are the mid-points of the sides BC, Ca and AB respectively of a triangle ABC, prove by vector method that Area of `Delta DEF` = 1/4 Area of `Delta ABC`
View SolutionProve that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
View SolutionIn Fig. 4.170, `A B C D` is a trapezium in which `A B D C` and `A B=2\ D C` . Determine the ratio of the areas of ` A O B` and ` C O D` . (FIGURE)
View SolutionIn a trapezium ABCD, O is the point of intesection of AC and BD, AB||CD and `AB = 2xx CD`. If the area of `triangleAOB= 84cm^(2)` . Find the area of `triangleCOD`.
View SolutionIn figure, DE||BC and the ratio of the areas of `triangleADE`and trapezium BDEC is 4:5 . Find the ratio of DE:BC . If BD = 2cm. Then find AD.
View SolutionX and Y are points on the sides AB and BC respectively of `triangleABC` such that XY||AC and XY divides `triangleABC` into two parts in area , find `(AX)/(AB)`
View SolutionCE and DE are equal chords of a cricule with centre O. if `angleAOB=90^(@)`find `ar(triangleCED) ar(triangleAOB)`
View SolutionIn the given figure `DE||BC and AD:DB =5:4`
Find the ratio `ar (Delta DEF) : ar (Delta CFB)`
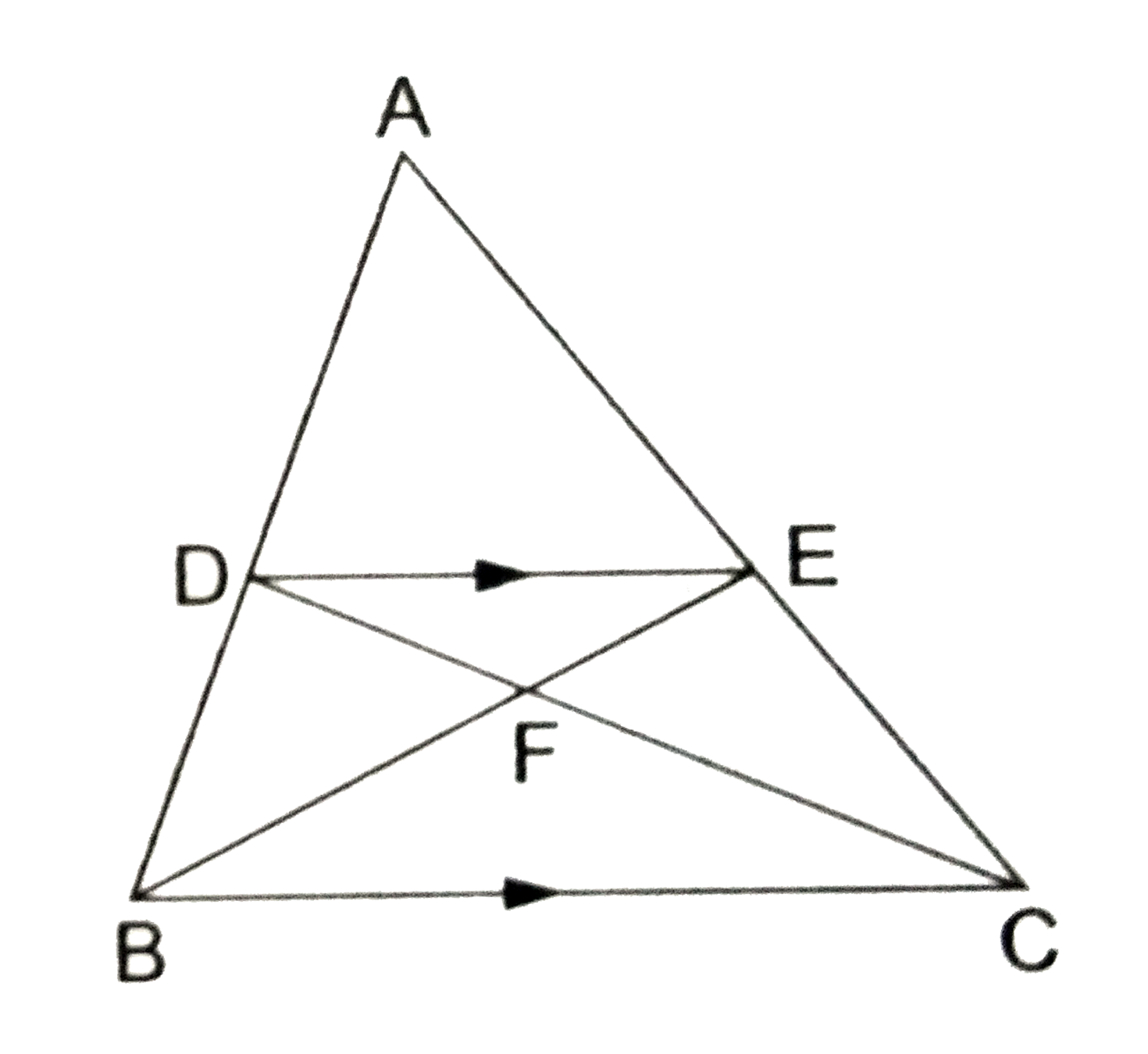
View SolutionIf two triangles are similar; prove that the ratio of corresponding sides is equal to the ratio of corresponding altitudes.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionIf two triangles are similar; prove that the ratio of the corresponding sides is same as the corresponding angle bisector segments.
View SolutionIn the adjoining figure ADE and ABC are two similar triangles, point D divides AB in the raito 2:1 and point E divides AC in the ratio 1:2 . If the area of `triangleADE` is 23 square units, then find the ar(`squareDECB)`.

View SolutionThe sides of a triangle are 5 cm, 8 cm and 11 cm respectively. Demtermine whether it is a right angled triangle or not.
View SolutionA ladder, `25` m long reaches a window of building `20` m, above the ground. The distance of the foot of the ladder from the building.
View SolutionTwo poles of height 6 meters and 11 meteras stand vertically on a plane ground. If the distance between their feet is 12 meters. Find the distance between their tops.
View SolutionP and Q are the mid-points of the sides CA and CB respectively of a `triangleABC` , right angled at C, prove that. (i) `4AQ^(2)=4AC^(2)+BC^(2)` (ii) `4BP^(2)=4BC^(2)+AC^(2)`
View SolutionThe perpendicular AD on the base BC of a `triangleABC` intersects BC at D, so that DB=3CD. Prove that `2AB^(2)= 2AC^(2)+BC^(2)`
View SolutionIn the given figure AD is perpendicular to BC produced, prove that :
`c^(2)=a^(2)+b^(2)=2ax`

View SolutionABC is a right traingle, right angled at C. if P is the length of perpendicular from C to AB and AB=c, BC=a and CA=b, then prove that (i) pc=ab (ii) `1/(p^(2)) = 1/(a^(2))+1/b^(2)`
View SolutionProve that the sum of the squares of the sides of rhombus is equal to the sum of the squares of its diagonals.
View SolutionIn an equilateral triangle `A B C` the side `B C` is trisected at `D`. Prove that `9\ A D^2=7\ A B^2`
View Solution`O` is any point inside a rectangle `ABCD`. then which of the following is correct:
View SolutionIn a triangle `A B C ,\ A C > A B` , `D` is the mid-point of `B C` and `A E_|_B C` . Prove that: (i) `A B^2=A D^2-B C D E+1/4B C^2` (ii) `A B^2+A C^2=2\ A D^2+1/2B C^2`
View SolutionIn ` P Q R ,\ \ Q M_|_P R` and `P R^2-P Q^2=Q R^2` . Prove that `Q M^2=P MxxM R`
View Solutionprove by vector method that the sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides.
View SolutionIn an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
View SolutionIn Figure, `A B C` is a right triangle right angled at `B` and points `Da n dE` trisect `B C` . Prove that `8A E^2=3A C^2+5A D^2dot`
View SolutionIn a `triangleABC` the angles at B and C are acute. If BE and CF be drawn perpendiculars on AC and AB respectivel, prove that
`BC^(2) = Abxx BF + AC xx EC`
View SolutionNazinia is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that h
View Solution
Solved Example questions and complete solutions for chapter TRIANGLES of NAGEEN MATHS (HINGLISH) of Class 10