Complete Solutions to EXERCISE of chapter সদৃশতা of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | সদৃশতা |
| NCERT BANGLISH (BANGLISH MEDIUM) | EXERCISE |
| Number Of Questions | 81 |
| Academic Year | 2023-24 |
`triangleABC` -এর BC -এর সমান্তরাল সরলরেখা AB ও AC -কে যথাক্রমে D ও E বিন্দুতে ছেদ করলে প্রমাণ করো যে,`(AB)/(DB)=(AC)/(EC)`
View Solution`triangleABC` -এর BC -এর সমান্তরাল সরলরেখা AB ও AC -কে যথাক্রমে D ও E বিন্দুতে ছেদ করলে প্রমাণ করো যে,`(AD)/(AB)=(AE)/(AC)`
View Solutionযুক্তি দিয়ে প্রমাণ করো যে, ' কোনো সরলরেখা যে-কোনো ত্রিভুজের দুটি বাহুকে বা তাদের বর্ধিতবাহুকে সমানুপাতে বিভক্ত করলে , তা তৃতীয় বাহুর সমান্তরাল হবে ' । ( প্রমাণ মূল্যায়নের অন্তর্ভুক্ত নয় )
View Solutionপাশের চিত্রে `triangleABC` -এর `DE |\|BC` , যদি AD = 5 সেমি. , DB = 6 সেমি. এবং AE = 7.5 সেমি. হয়, তবে AC -এর দৈর্ঘ্য হিসাব করে লেখো ।
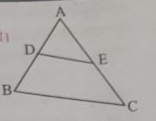
View Solutionযদি `triangleABC` -এর `BC |\| DE` , `(AD)/(BD)= 2/5` এবং AC = 21 সেমি. হয়, তবে AE -এর মান হিসাব করে লেখো ।
View SolutionABC ত্রিভুজের BC বাহুর সমান্তরাল সরলরেখা AB ও AC -কে যথাক্রমে D ও E বিন্দুতে ছেদ করেছে । AE = 2 AD হলে, DB : EC -এর মান হিসাব করে লেখো ।
View Solutionপাশের চিত্রে `PQ |\|AB` এবং `PR |\|AC` হলে, প্রমাণ করো যে, `QR |\|BC`
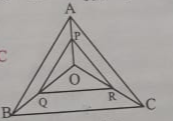
View Solutionএকটি সরলরেখা `triangleABC` -এর AB ও AC -কে যথাক্রমে D ও E বিন্দুতে এমনভাবে ছেদ করল যে `(AD)/(DB)=(AE)/(EC)` হলো । যদি `angleADE=angleACB` হয়, প্রমাণ করো যে, `triangleABC` সমদ্বিবাহু ত্রিভুজ ।
View SolutionABCD একটি ট্রাপিজিয়াম অঙ্কন করেছো যার `AB |\|DC` , AB -এর সমান্তরাল একটি সরলরেখা অঙ্কন করেছো যা AD ও BC -কে যথাক্রমে E ও F বিন্দুতে ছেদ করেছে । প্রমাণ করো যে, AE : ED = BF : FC
View Solutionথ্যালাসের বিপরীত উপপাদ্যের সাহায্যে প্রমাণ করো যে, ত্রিভুজের মধ্যবিন্দুরদ্বয়ের সংযোজক সরলরেখাংশ তৃতীয় বাহুর সমান্তরাল ।
View SolutionABCD একটি ট্রাপিজিয়াম অঙ্কন করেছো যার `AB |\|DC` , AD ও BC -এর উপর যথাক্রমে P ও Q এমন দুটি বিন্দু নিলে যাতে AP : PD =BQ : QC হয় । প্রমাণ করো যে, `PQ |\|DC`
View Solutionযুক্তি দিয়ে প্রমাণ করো যে একটি ত্রিভুজের কোনো কোণের অন্তসমদ্বিখণ্ডক বা বহিসমদ্বিখণ্ডক কোণটির বিপরীত বাহুকে অন্তঃস্থভাবে বা বহিঃস্থভাবে কোণসংলগ্ন বাহুদুটির দৈর্ঘ্যের অনুপাতে বিভক্ত করে ।
View Solutionযুক্তি দিয়ে প্রমাণ করো যে, একটি ত্রিভুজের কোনো কোণ থেকে অঙ্কিত কোনো সরলরেখা যদি ওই কোণের বিপরীত বাহুকে অন্তঃস্থভাবে বা বহিঃস্থভাবে ত্রিভুজের কোণ সংলগ্ন বাহু দুটির দৈর্ঘ্যের অনুপাতে বিভক্ত করে তাহলে সরলরেখাটি কোণটির অন্তসমদ্বিখণ্ডক বা বহিসমদ্বিখণ্ডক হবে ।
View Solution`triangleABC` -এর BC বাহুর সমান্তরাল সরলরেখা AB ও AC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে । PB = AQ, AP = 9 একক , QC = 4 একক হলে, PB -এর দৈর্ঘ্য হিসাব করে লেখো ।
View Solution`triangleABC` -এর BC বাহুর সমান্তরাল সরলরেখা AB ও AC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে । PB -এর দৈর্ঘ্য AP -এর দৈর্ঘ্যের দ্বিগুণ এবং QC -এর দৈর্ঘ্য AQ -এর দৈর্ঘ্যের চেয়ে 3 একক বেশি হলে, AC -এর দৈর্ঘ্য কত হবে, হিসাব করে লেখো ।
View Solution`triangleABC` -এর BC বাহুর সমান্তরাল সরলরেখা AB ও AC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে । যদি AP = QC, AB -এর দৈর্ঘ্য 12 একক এবং AQ -এর দৈর্ঘ্য 2 একক হয়, তবে CQ -এর দৈর্ঘ্য কত হবে, হিসাব করে লেখো ।
View Solution`trianglePQR` -এর PQ ও PR বাহুর উপর যথাক্রমে X ও Y দুটি বিন্দু নিলে । PX = 2 একক, XQ = 3.5 একক, YR = 7 একক এবং PY = 4.25 একক হলে, XY ও QR পরস্পর সমান্তরাল হবে কিনা যুক্তি দিয়ে লেখো ।
View Solution`trianglePQR` -এর PQ ও PR বাহুর উপর যথাক্রমে X ও Y দুটি বিন্দু নিলে । PQ = 8 একক, YR = 12 একক, PY = 4 একক এবং PY -এর দৈর্ঘ্য XQ -এর দৈর্ঘ্যের চেয়ে 2 একক কম হলে, XY ও QR সমান্তরাল হবে কিনা যুক্তি দিয়ে লেখো ।
View Solutionপ্রমাণ করো যে, কোনো ত্রিভুজের একটি বাহুর মধ্যবিন্দু দিয়ে অঙ্কিত দ্বিতীয় বাহুর সমান্তরাল সরলরেখা তৃতীয় বাহুকে সমদ্বিখণ্ডিত করে । [ থ্যালাসের উপপাদ্যের সাহায্যে প্রমাণ করো ]
View Solution`triangleABC` -এর AD মধ্যমার উপর P একটি বিন্দু । বর্ধিত BP ও CP যথাক্রমে AC ও AB -কে Q ও R বিন্দুতে ছেদ করেছে । প্রমাণ করো যে, `RQ |\|BC`
View Solution`triangleABC` -এর BC বাহুর সমান্তরাল সরলরেখা AB ও AC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে। PB -এর দৈর্ঘ্য AP -এর দৈর্ঘ্যের দ্বিগুন এবং QC -এর দৈর্ঘ্য AQ -এর দৈর্ঘ্যের চেয়ে 3 একক বেশি হলে, AC -এর দৈর্ঘ্য কত হবে হিসাব করে লিখি।
View Solutionপ্রমাণ করো যে, ট্রাপিজিয়ামের তির্যক বাহুগুলির মধ্যবিন্দু দুটির সংযোজক সরলরেখাংশ সমান্তরাল বাহুগুলির সমান্তরাল ।
View Solution`triangleABC` -এর AD মধ্যমার উপর P একটি বিন্দু । বর্ধিত BP ও CP যথাক্রমে AC ও AB -কে Q ও R বিন্দুতে ছেদ করেছে । প্রমাণ করো যে, `RQ |\|BC`
View Solutionএকই ভূমি QR-এর উপর এবং QR-এর একই দিকে দুটি ত্রিভুজ `trianglePQR` এবং `triangleSQR` এর ক্ষেত্রফল সমান । ত্রিভুজ দুটির ভরকেন্দ্র যথাক্রমে F ও G হলে প্রমান করো যে, `FG|\|QR` ।
View Solutionপ্রমাণ করো যে, কোনো সমদ্বিবাহু ট্রাপিজিয়ামের সমান্তরাল বাহুদুটির যে-কোনো একটির সংলগ্ন কোণ দুটি সমান ।
View Solution`triangleABC` ও `triangleDBC` সদৃশকোণী। অতএব তারা
View Solutionনীচের বিবৃতিটি সত্য না মিথ্যা লেখো । দুটি সদৃশ ত্রিভুজ সর্বদা সর্বসম ।
View Solutionনীচের বিবৃতিটি সত্য না মিথ্যা লেখো চিত্রে, `DE |\|BC` হলে, `(AB)/(BD)= (AC)/(CE) ` হবে ।
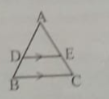
View Solutionশূন্যস্থান পূরণ করো ত্রিভুজের যে-কোনো বাহুর সমান্তরাল সরলরেখা অপর দুটি বাহুকে বা তাদের বর্ধিতাংশকে __ বিভক্ত করে ।
View Solutionশূন্যস্থান পূরণ করো ত্রিভুজের ভূমি একই সরলরেখায় অবস্থিত এবং ত্রিভুজ দুটির অপর শীর্ষবিন্দুটি সাধারন হলে ত্রিভুজ দুটির ক্ষেত্রফলের অনুপাত ভূমির দৈর্ঘ্যের অনুপাতের __ ।
View Solutionশূন্যস্থান পূরণ করো । একটি ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের সমান্তরাল সরলরেখা অপর বাহুদ্বয়কে __ বিভক্ত করে ।
View Solutionপাশের চিত্রে, ABC ত্রিভুজে `(AD)/(DB)= (AE)/(EC)` এবং `angleADE=angleACB` হলে, বাহুভেদে ABC ত্রিভুজটি কী ধরনের লেখো ।
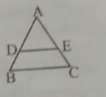
View Solutionপাশের চিত্রে, `DE |\|BC` এবং AD : DB = 3 : 5 হলে, `triangleADE` -এর ক্ষেত্রফল : `triangleCDE` -এর ক্ষেত্রফল কত তা লেখো ।
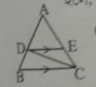
View Solutionপাশের চিত্রে, `LM |\|AB` এবং AL = ( x-3 ) একক, AC = 2x একক, BM = ( x-2 ) একক এবং BC = ( 2x+3 ) একক হলে, x -এর মান নির্ণয় করো ।
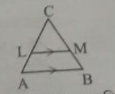
View Solutionপাশের চিত্রে, `DE |\| BC` , `BE |\| XC` এবং `(AD)/(DB)=2/1` হলে, `(AX)/(XB)` -এর মান নির্ণয় করো ।
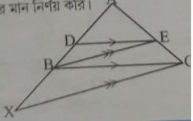
View Solution[চিত্র] নীচের কোন ত্রিভুজ জোড়া সদৃশ হিসাব করে লেখ
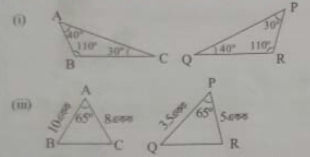
View Solution[চিত্র]নীচের কোন ত্রিভুজ জোড়া সদৃশ হিসাব করে লেখ
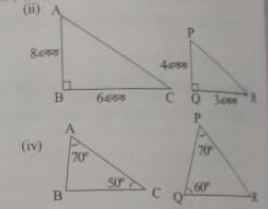
View Solutionচিত্র]নীচের ত্রিভুজ জোড়া দেখ ও `/_A`-এর মান হিসাব করে লেখ
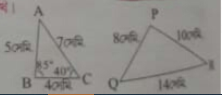
View Solutionআমাদের মাঠে 6 সেমি. দৈর্ঘ্যের একটি কাঠির 4 সেমি. দৈর্ঘ্যের ছায়া মাতিতে পড়েছে । ওই একই সময়ে যদি একটি উঁচু টাওয়ারের ছায়ার দৈর্ঘ্য 28 মিটার হয়, তবে টাওয়ারের উচ্চতা কত হবে হিসাব করে লেখ।
View Solutionএকটি লম্ব বৃত্তাকার শঙ্কুর উচ্চতা 1 মিটার এবং তার ঘনফল 75`pi` ঘনমিটার হলে শঙ্কুটির সমগ্রতলের ক্ষেত্রফল নির্ণয় করো।
View Solutionতিনটি সমবিন্দু সরলরেখাকে দুটি সমান্তরাল সরলরেখা যথাক্রমে A,B,C ও X,Y,Z বিন্দুতে ছেদ করেছে, প্রমাণ কর যে , AB:BC=XY:YZ
View SolutionPQRS একটি ট্রাপিজিয়াম অঙ্কন করেছ যার `PQ||SR`,PR ও QS কর্ণ দুটি O বিন্দুতে পরস্পরকে ছেদ করলে, প্রমাণ কর যে, OP:OR=OQ:OS,যদি SR=2PQ হয়, তাহলে প্রমাণ কর যে,O বিন্দু কর্ণ দুটির প্রত্যেকটির সমত্রিখন্ডক বিন্দুর একটি বিন্দু হবে।
View SolutionPQRS একটি সামান্তরিক। S বিন্দুগামী একটি সরলরেখা PQ এবং বর্ধিত RQ -কে যথাক্রমে X ও Y বিন্দুতে ছেদ করলে, প্রমাণ কর যে ,`PS:PX=QY:QX=RY:RS`।
View Solutionদুটি সূক্ষ্মকোণী ত্রিভুজ `/_\ ABC`ও `/_\PQR`সদৃশকোণী । তাদের পরিকেন্দ্র যথাক্রমে X ও Y,BC ও QR অনুরূপ বাহু হলে, প্রমাণ কর যে, `BX:QY=BC:QR `।
View Solutionকোনো বৃত্তের PQ ও RS দুটি জ্যা বৃত্তের অভ্যন্তরে X বিন্দুতে পরস্পরকে ছেদ করেছে। P,S ও R,Q যুক্ত করে,প্রমাণ কর যে `/_\ PXS`ও `/_\RXQ`,সদৃশকোণী । এর থেকে প্রমাণ কর যে `PX*XQ=RX*XS`
View Solutionএকটি বৃত্তের দুটি জ্যা পরস্পরকে অন্তঃস্থভাবে ছেদ করলে একটির অংশদ্বয়ের আয়তক্ষেত্র অপরটির অংশদ্বয়ের আয়তক্ষেত্রের সমান হবে।
View Solutionএকটি সরলরেখার উপরP এবংQ দুটি বিন্দু।P এবংQ বিন্দুতে সরলরেখাটির উপর যথাক্রমে PR এবং QS লম্ব । PS এবং QR পরস্পরকেO বিন্দুতে ছেদ করে।OT,PQ এর উপর লম্ব। প্রমাণ করো যে,`1/(OT)=1/(PR) + 1/(QS)`।
View Solutionবার্ষিক 10% চক্রবৃদ্ধি হার সুদে 5000 টাকা কত বছরে 6655 টাকা হবে?
View Solutionপ্রমান করো যে, একটি সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজের ওপর লম্ব অঙ্কন করলে লম্বের দুপাশে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা মূল ত্রিভুজের সঙ্গে সদৃশ এবং তারা পরস্পর সদৃশ ।
View SolutionABC সমকোণী ত্রিভুজের `/_A` সমকোণ। সমকৌণিক বিন্দু A থেকে অতিভুজ BC-এর উপর AD লম্ব অঙ্কন করা হল । প্রমাণ কর যে `AB^2=BC.BD`
View SolutionABC সমকোণী ত্রিভুজের `/_A` সমকোণ। সমকৌণিক বিন্দু A থেকে অতিভুজ BC-এর উপর AD লম্ব অঙ্কন করা হল । প্রমাণ কর যে `AD^2=BD.CD`
View SolutionABC সমকোণী ত্রিভুজের `/_A` সমকোণ। সমকৌণিক বিন্দু A থেকে অতিভুজ BC-এর উপর AD লম্ব অঙ্কন করা হল । প্রমাণ কর যে `AC^2=BC.CD`
View Solution`/_\ ABC`-এর `/_ ABC=90^@` এবং `BDbotAC` , যদি `BD=6`সেমি. এবং `AD=4`সেমি হয়। তবে BC-এর দৈর্ঘ্য হিসাব করে লেখ।
View Solution`/_\ ABC`-এর `/_ ABC=90^@` এবং `BDbotAC` , যদি `AB=6`সেমি. এবং `BD=3`সেমি. এবং `CD=5.4`সেমি. হয়। তবে BC বাহুর দৈর্ঘ্য হিসাব করে লেখ।
View Solution`/_\ ABC`-এর শীর্ষবিন্দু A থেকে BC বাহুর উপর AD লম্ব অঙ্কন করা হল । যদি `(BD)/(DA)= (DA)/(DC)`হয়, তবে প্রমাণ কর যে ABC একটি সমকোণী ত্রিভুজ।
View Solutionযদি কোনো সমকোণী ত্রিভুজ ABC সমকৌণিক বিন্দু A থেকে অতিভুজের উপর লম্ব অঙ্কন করা হলে এবং যদি AC, AB, BC ক্রমিক সমানুপাতী হয়, তবে প্রমাণ কর যে অতিভুজটির বৃহত্তম অংশ ত্রিভুজটির ক্ষুদ্রতম বাহুর সমান হবে
View Solutionএকটি বৃত্ত অঙ্কন করা হল যার ব্যাস AB এবং কেন্দ্র O, বৃত্তের উপরিস্থিত কোনো বিন্দু P থেকে AB ব্যাসের উপর একটি লম্ব অঙ্কন করা হল, যা AB থেকে N বিন্দু তে ছেদ করল। প্রমাণ কর যে, `PB^2=AB.BN`
View Solutionদুটি বৃত্ত পরস্পরকে A বিন্দু তে বহিস্পর্শ করেছে। PQ ওই দুটি বৃত্তের একটি সরল সাধারণ স্পর্শক। যদি বৃত্ত দুটির ব্যাসার্ধের দৈর্ঘ্য যথাক্রমে r ও r'হয়, তাহলে প্রমাণ কর যে `PQ^2=4rr'`
View Solutionএকটি ত্রিভুজের কোণ তিনটির অনুপাত 2 : 3 : 4 হলে, ত্রিভুজটির ক্ষুদ্রতম কোণটির বৃত্তীয় মান নির্ণয় করো।
View Solution`/_\ ABC`-এর `/_ABC=90^@`এবং `BDbotAC`, যদি `BD=8`সেমি. এবং `AD=5`সেমি হয়, তবে CD-এর দৈর্ঘ্য হিসাব করে লেখ
View SolutionABC সমকোণী ত্রিভুজ যার `/_B`সমকোণ এবং `BDbotAC`, যদি `AD=4`সেমি হয়, এবং `CD=16`সেমি. হয়, তবে BD এর দৈর্ঘ্য হিসাব করে লেখ
View Solution6500 টাকার 2 বছরে সমূলে চক্রবৃদ্ধি 7865 টাকা হলে বার্ষিক চক্রবৃদ্ধি সুদের হার নির্ণয় করো।
View SolutionAB- কে ব্যাস করে একটি অর্ধবৃত্ত অঙ্কন করা হল। AB-এর উপর যে কোনো বিন্দু C থেকে AB-এর উপর লম্ব অঙ্কন করা হল যা অর্ধবৃত্তকে D বিন্দুতে ছেদ করেছে। প্রমাণ কর যে, CD, AC ও BC-এর মধ্যসমানুপাতী
View Solutionসমকোণী ত্রিভুজ `/_\ABC` -এর `/_A= 90^@`। অতিভুজ BC-এর ওপর AD লম্ব । প্রমাণ করো যে,`(/_\ABC)/(/_\ACD)=(BC^2)/(AC^2)`
View SolutionO কেন্দ্রীয় বৃত্তের AB ব্যাস। A বিন্দু দিয়ে অঙ্কিত একটি সরলরেখা বৃত্তকে C বিন্দুতে এবং B বিন্দুতে অঙ্কিত স্পর্শককে D বিন্দুতে ছেদ করে। প্রমাণ কর যে, `BD^2=AD.DC
View SolutionO কেন্দ্রীয় বৃত্তের AB ব্যাস। A বিন্দু দিয়ে অঙ্কিত একটি সরলরেখা বৃত্তকে C বিন্দুতে এবং B বিন্দুতে অঙ্কিত স্পর্শককে D বিন্দুতে ছেদ করে। প্রমাণ কর যে, যে কোনো সরলরেখার জন্য AC এবং AD দ্বারা গঠিত আয়তক্ষেত্রের ক্ষেত্রফল সর্বদা সমান।
View Solution[চিত্র] পাশের চিত্রে, `/_ACB=/_BAD`এবং `ADbotBC`, AC=15 সেমি., AB= 20সেমি., BC=25সেমি. হলে, AD-এর দৈর্ঘ্য কত তা লেখ
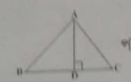
View Solution[চিত্র] পাশের চিত্রে, `/_ABC=90^@`এবং `BDbotAC`,যদি `AB= 30` সেমি., `BD= 24` সেমি. এবং ` AD=18` সেমি হলে, CD-এর দৈর্ঘ্য কত তা লেখ
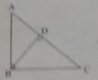
View Solution[চিত্র] পাশের চিত্রে, `/_ABC=90^@`এবং `BDbotAC`,যদি `BD=8`সেমি. এবং `AD=4`সেমি হয়, তাহলে CD-এর দৈর্ঘ্য কত তা লেখ
View SolutionABCD ট্রাপিজিয়ামের `BC||AD`এবং `AD=4`সেমি.। AC ও BD কর্ণদ্বয় এমনভাবে O বিন্দুতে ছেদ করে যে `(AO)/(OC)=(DO)/(OB)=1/2`হয়। BC-এর দৈর্ঘ্য কত তা লেখ
View Solutionত্রিভুজABCও ত্রিভুজDEF সদৃশ।`triangle ABC`ও`triangleDEF`এরAB, BCও CA বাহুগুলির অনুরূপ বাহুগুলি যথাক্রমে DE,EFও DF।`angleA=47^@`এবং`angleE=83^@`হলে`angleC`এর পরিমাপ লেখ।
View Solutionনীচের বিবৃতিটি সত্য না মিথ্যা লেখ: দুটি চতুর্ভুজের অনুরূপ কোণগুলি সমান হলে চতুর্ভুজ দুটি সদৃশ
View Solution[চিত্র]নীচের বিবৃতিটি সত্য না মিথ্যা লেখ: `/_ADE=/_ACB`হলে `/_\ADE~/_\ACB`

View Solutionনীচের বিবৃতিটি সত্য না মিথ্যা লেখ: `/_\PQR`-এর QR বাহুর উপর D এমন একটি বিন্দু যে `PD bot QR`, সুতরাং `/_\PQD` ~ `/_\RPD`
View Solutionদুটি ত্রিভুজ সদৃশ হবে যদি তাদের ________ বাহুগুলি সমানুপাতী হয়।
View Solution`/_\ABC` ও `/_\DEF`-এর পরিসীমা যথাক্রমে 30 সেমি। এবং 18 সেমি। `/_\ABC`~ `/_\DEF`, BC ও EF অনুরূপ বাহু। যদি BC =9সেমি. হয়, তাহলে EF= ________ সেমি.।
View Solution`/_\ ABC`ও `/_\ DEF`-এ `(AB)/(DE)=(BC)/(FD)=(AC)/(EF)`হলে,
View Solution`/_\ DEF`ও `/_\PQR`-এ `/_D=/_Q`এবং `/_R=/_E`হলে, নীচের কোন টি সঠিক নয় লেখ
View SolutionABC ও DEF ত্রিভুজে `/_A=/_E=40^@`, `AB:ED=AC:EF` এবং `/_F=65^@` হলে `/_B`
View Solution`/_\ ABC`ও `/_\PQR`-এ `(AB)/(QR)=(BC)/(PR)=(CA)/(PQ)`হলে
View SolutionABC ত্রিভুজে `AB= 9` সেমি., `BC= 6` সেমি `CA=7.5সেমি ` । DEF ত্রিভুজে BC বাহুর অনুরূপ বাহু EF, `EF=8`সেমি. এবং `/_\ DEF`~ `/_\ ABC` হলে `/_\ DEF`-এর পরিসীমা
View Solution
EXERCISE questions and complete solutions for chapter সদৃশতা of NCERT Mathematics (Bengali) of Class 10