Complete Solutions to Exercise 16A of chapter AREA OF CIRCLE, SECTOR AND SEGMENT of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | AREA OF CIRCLE, SECTOR AND SEGMENT |
| RS AGGARWAL | Exercise 16A |
| Number Of Questions | 65 |
| Academic Year | 2023-24 |
The circumference of a circle is 39.6 cm. Find its area.
View SolutionThe area of a circle is `98.56cm^(2)`. Find its circumference.
View SolutionThe circumference of a circle exceeds its diameter by 45 cm. Find the circumference of the circle.
View SolutionThe copper wire, when bent in the form of a square, encloses an area of 484 `c m^2` . If the same wire is bent in the form of a circle, find the area enclosed by it.
View SolutionA wire when bent in the form of an equilateral triangle encloses an area of `121sqrt(3)cm^(2)`. If the same wire is bent into the form of a circle, what will be the area of the circle? [Take `pi=22/7`]
View SolutionThe length of a chain used as the boundary of a semicircular park is `108m`. Find the area of the park.
View SolutionThe sum of the radii of two circles is 7 cm, and the difference of their circumferences is 8 cm. Find the circumferencs of the circles.
View SolutionFind the area of a ring whose outer and inner radii are respectively 23 cm and 12 cm.
View Solution(i) A path of 8 m width runs around the outside of a circular park whose radius is 17 m. Find the area of the path.
(ii) A park of the shape of a circle of diameter 7m. It is surrounded by a path of width of 0.7 m. Find the expenditure of cementing the path, if its cost is Rs. 110 per sq m.
View SolutionA race track is in the form of a ring whose inner circumference is 352 m, and the outer circumference is 396 m. Find the width of the track.
View SolutionA sector is cut off from a circle of radius 21 cm. The angle of the sector is `120^(@)`. Find the length of its arc and the area.
View SolutionA chord PQ of a circle of radius 10 cm makes an angle of `60^(@)` at the centre of the circle. Find the area of the major and the minor segment
View SolutionThe length of an arc of a circle, subtending an angle of `54^(@)` at the centre is 16.5cm. Calculate the radius, circumference and area of the circle.
View SolutionThe radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
View SolutionFind area of the minor segment formed by a chord `12cm` long in a circle of radius `12cm` . [use `pi=3.14`, `sqrt(3)=1.732`]
View SolutionA chord 10cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the area of both the segments.
View SolutionFind the area of both the segments of a circle of raidus 42 cm with central angle `120^(@)`. [Given `sin 120^(@)=(sqrt(3))/2` and `sqrt(3)=1.73`]
View SolutionA chord of a circle of radius 30 cm makes an angle of `60^(@)` at the centre of the circle. Find the areas of the minor and major segments. [Take `pi=314` and `sqrt(3)=1.732`]
View SolutionIn a circle of radius 10.5cm the minor arc is one-fifth of the major arc. Find the area of the sector corresponding to the major arc.
View SolutionThe short and long hands of a clock are 4cm and 6cm long respectively. Find the sum of distances travelled by their tips in 2 days. `(T a k epi(22)/7)`
View SolutionFind the area of a quadrant of a circle whose circumference is 88 cm.
View SolutionA rope by which a cow is tethered is increased from 16 m to 23 m. How much additional ground does it have now to graze?
View SolutionA horse is placed for grazing inside a rectangular field 70m by 52m and is tethered to one corner by a rope 21m long. On how much area can it graze?
View SolutionA horse is tethered to one corner of a field which is in the shape of an equilateral triangle of side 12 m. If the length of the rope is 7m, find the area of the field which the horse cannot graze. Take `sqrt(3)=1.732`. Write the answer correct to 2 places of decimal.
View SolutionFour cows a tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed ? [Take `pi=3.14`]
View SolutionIn the given figure `OPQR` is a rhombus, three of whose vertices lie on a circle with centre O. If the ara of the rhomus is `32sqrt(3)cm^(2)`, find the radius of the circle.

View SolutionThe side of a square is 10 cm. Find the area of circumscribed and inscribed circles.
View SolutionIf a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
View SolutionThe area of a circle inscribed in an equilateral triangle is `154\ c m^2` . Find the perimeter of the triangle. `[U s e\ \ pi=22//7a n d\ sqrt(3)=1. 73]`
View SolutionThe radius of the wheel of a vehicle is 42 cm. How many revolutioins will it complete in a 19.8-km-long journey?
View SolutionThe wheels of the locomotive of a train are 2.1 m in radius. They make 75 revolutions in one minute. Find the speed of the train in km per hour.
View SolutionThe wheels of a car make 2500 revolutions in covering a distance of 4.95 km. Find the diameter of a wheel.
View SolutionA boy is cycling such that the wheels of the cycle are making 140 revolutions per minute. If the diameter of the wheel is 60 cm, calculate the speed per hour with which the boy is cycling.
View SolutionThe wheel of a motor cycle is of radius 35 cm. How many revolutions per minute must the wheet make, so as to keep a speed of 66 km/h ?
View SolutionThe diameters of the fron and rear wheels of a tractor are 80 cm and 2 m respectively. Find the number of revolutions that a rear wheel makes to cover the distance which the front wheel covers is 800 revolutions.
View SolutionFour equal circles are described about the four corners of square so that each touches two of the others, as shown in the figure. Find the area of the shaded region, if each side of the square measures `14` cm.

View SolutionFour equal circles each of radius 5 cm, touch each other, as shown in the figure. Find the area included between them.
[Take `pi=3.14`]

View SolutionFour circles each of radius `' a '` units touch one another. The area enclosed between them in square units is `(a^2)/7` (b) `3a^2` (c) `(6a^2)/7` (d) `(41 a^2)/7`
View SolutionThree equal circles, each of radius 6 cm, touch one another as shown in the figure. Find the area enclosed between them.
[Take `pi=3.14` and `sqrt(3)=1.732`]

View SolutionIf three circles of radius `a` each are drawn such that each touches the other two, prove that the area included between them is equal to `4/25a^(2)`.
[Take `sqrt(3)=1.73` and `pi=3.14`]
View SolutionIn the given figure ABCD s a trapezium of area `24.5cm^(2)`. If `AD||BC, /_DAB=90^(@),AD=10cm,BC=4cm` and ABE is quadrant of a circle then find the area of the shaded region.

View SolutionABCD is a field in the shape of a trapezium, `AD||BC,/_ABC=90^(@)` and `/_ADC=60^(@)`. For sectors are formed with centres A,B,C and D, as shown in the figure. The radius of each sector is 14 m. Find the following:
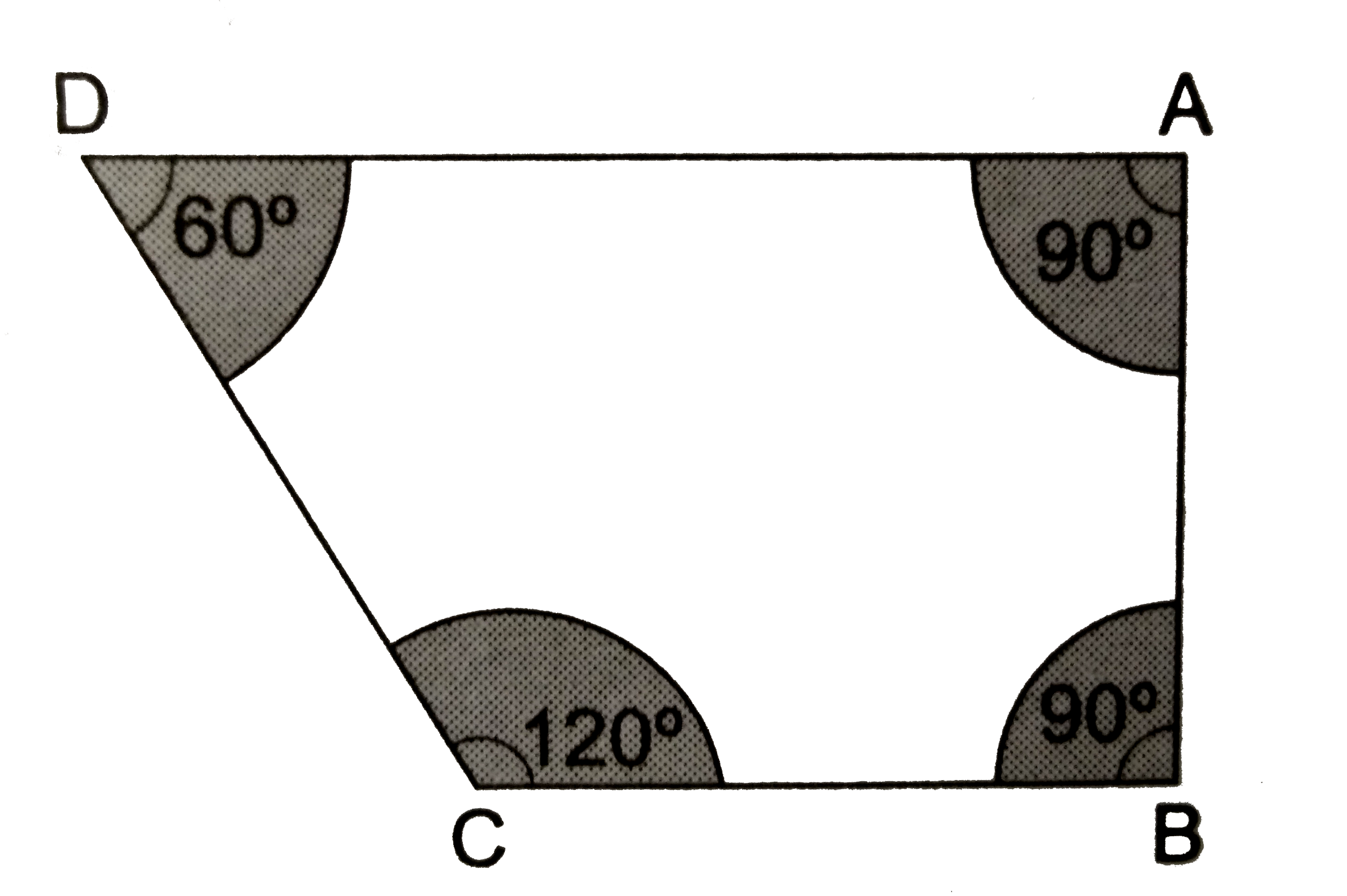
(i) Total area of the four sectors,
(ii) area of the remaining portion, given that `AD=55m, BC=45m` and `AB=30m`.
View SolutionFind the area of the shaded region in the given figure, where a circular of arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made. [ Use `sqrt(3)=1.73` and `pi=3.14`]

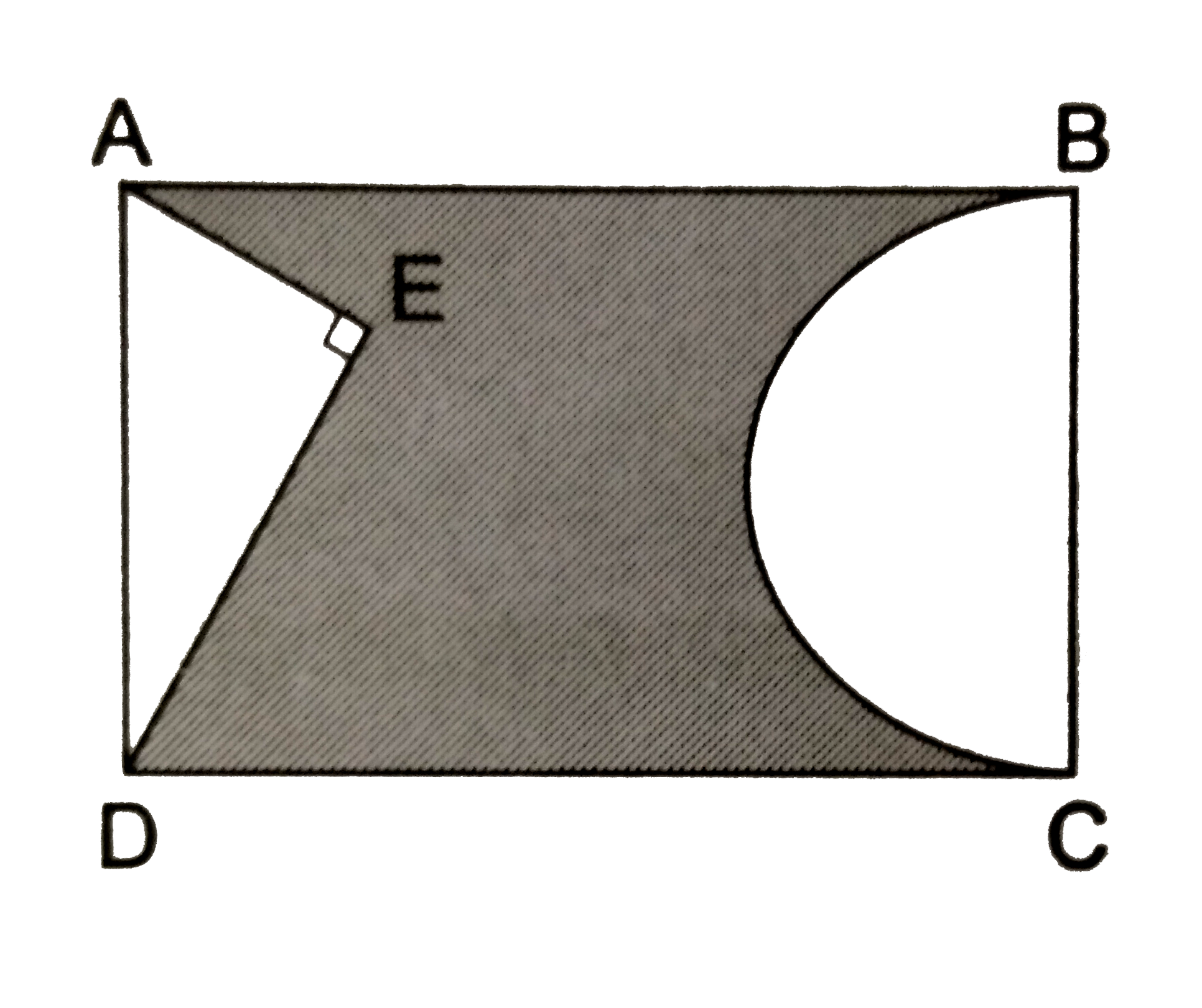
View SolutionIn the given figure, ABCD is a rectangle with `AB=80cm` and `BC=70cm, /_AED=90^(@)` and `DE=42cm`. A semicirle is drawn, taking BC a diameter. Find the area of the shaded region.
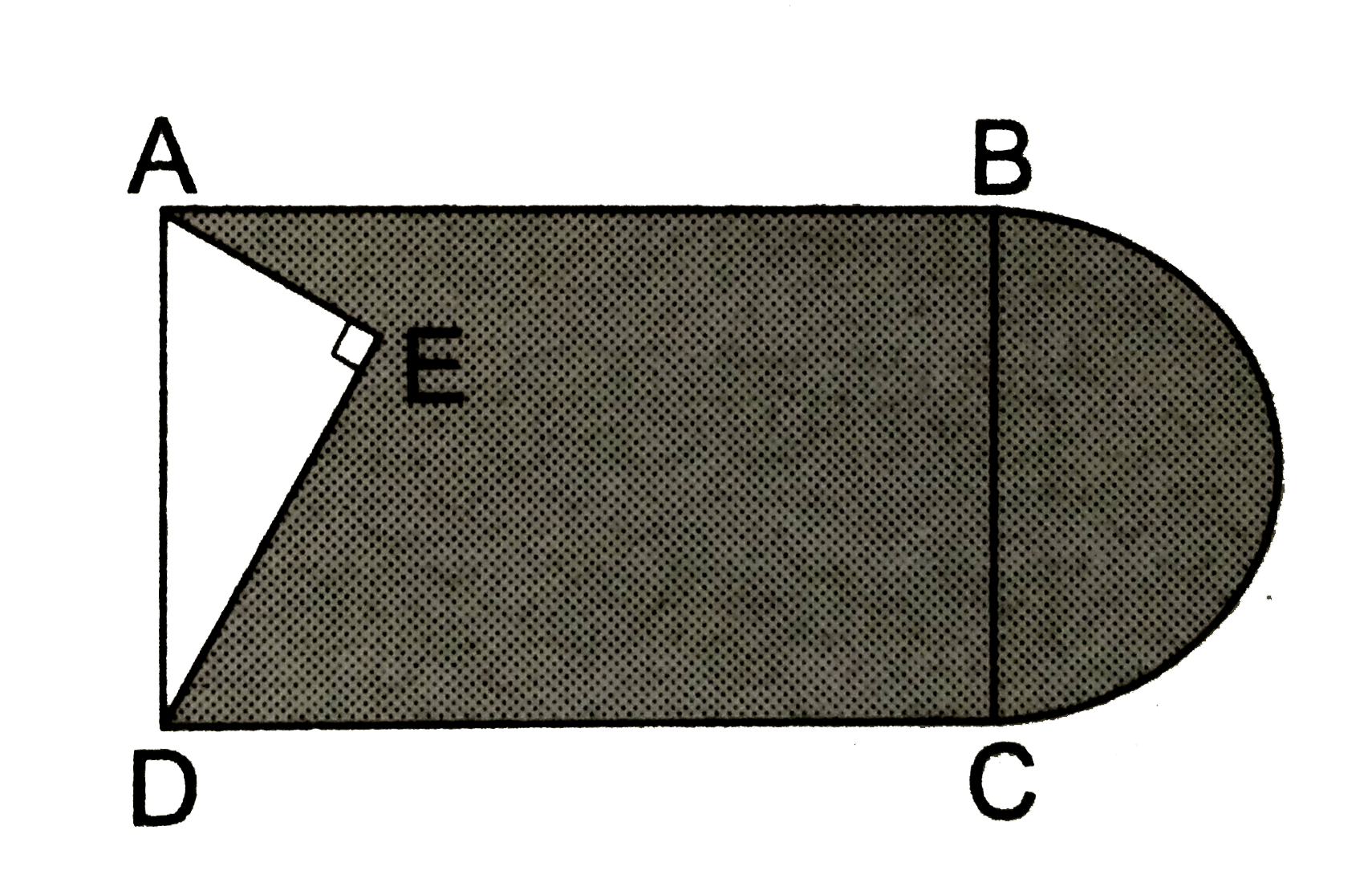
View SolutionIn the given figure, from a rectangular region ABCD with `AB=20cm` a right triangle AED with `AE=9cm` and `DE=12cm`, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside the region. The area of the shaded region.
[Use `pi=3.14`]
View SolutionIn the given figure `O` is the centre of the circle with `AC=24cm, AB=7cm` and `/_BOD=90^(@)`. Find the area of shaded region.
[Use `pi=3.14`]

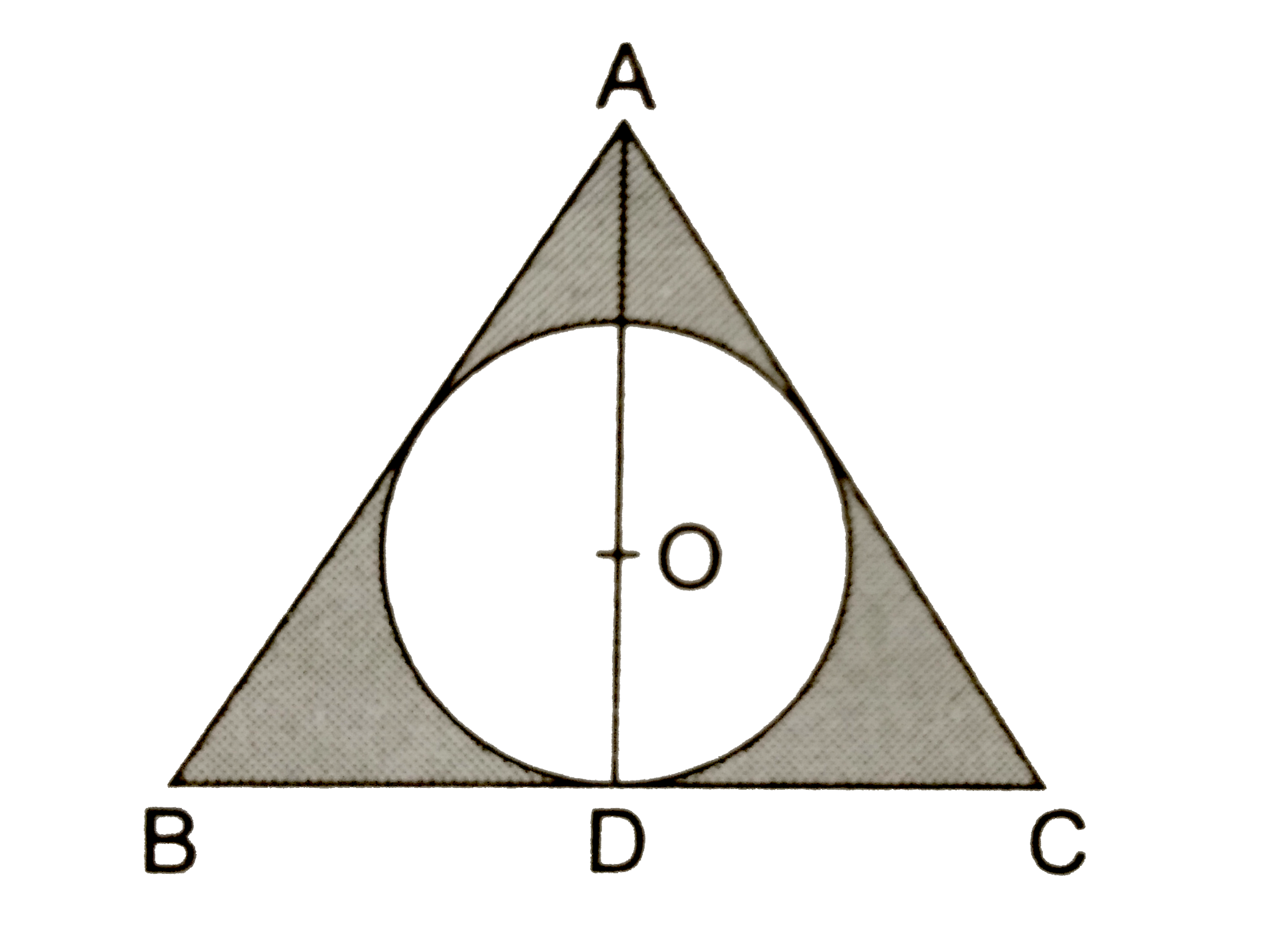
View SolutionIn the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region. [Use `sqrt(3)=1.73` and `pi=3.14`]
View SolutionThe perimeter of the quadrant of a circle is 25 cm. Find the area.
View SolutionA chord of a circle of radius 10 cm subtends a right angle at the centre. The area of the minor segments (given `pi=3.14)` is
View SolutionThe radius of a circular garden is 100m. There is a road 10m wide, running all around it. Find the area of the road and the cost of levelling it at Rs. 20 per `m^(2)`. [Use `p=3.14`]
View SolutionThe area of an equilateral triangle is `49sqrt(3)c m^2` . Taking each angular point as shown in Figure. Find the area of the triangle not included in the circle.
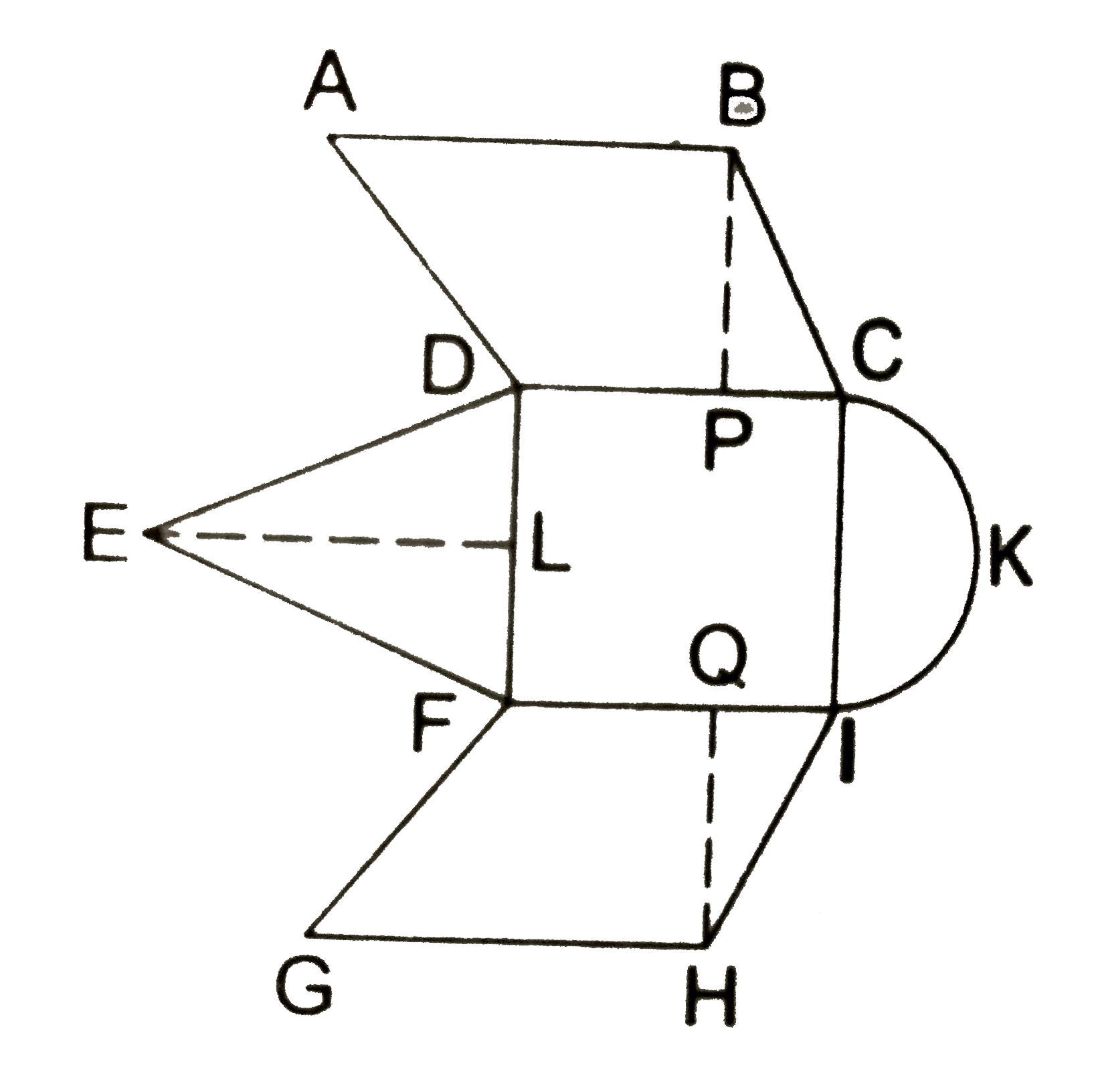
View SolutionA child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, `BP_|_CD, HQ_|_FI` and `EL_|_DF`. If `CD=8 cm, BP=HQ=4cm` and `DE=EF=5cm`, find the area of the whole figure. [Take `pi=3.14`]
View SolutionA circular disc of radius 6 cm is divided into three sectors with central angles `90^(@), 120^(@)` and `150^(@)`. What part of the whole circle is the sector with central angle `150^(@)`? Also, calculate the ratio of the areas of the three sectors.
View SolutionA round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm then find the total area of the design. [Use `sqrt(3)=1.732` and `pi=3.14`]

View SolutionIn the given figure `PQ=24cm, PR=78cm` and `O` is the centre of the circle. Find the area of the shaded region. [Take `pi=3.14`]
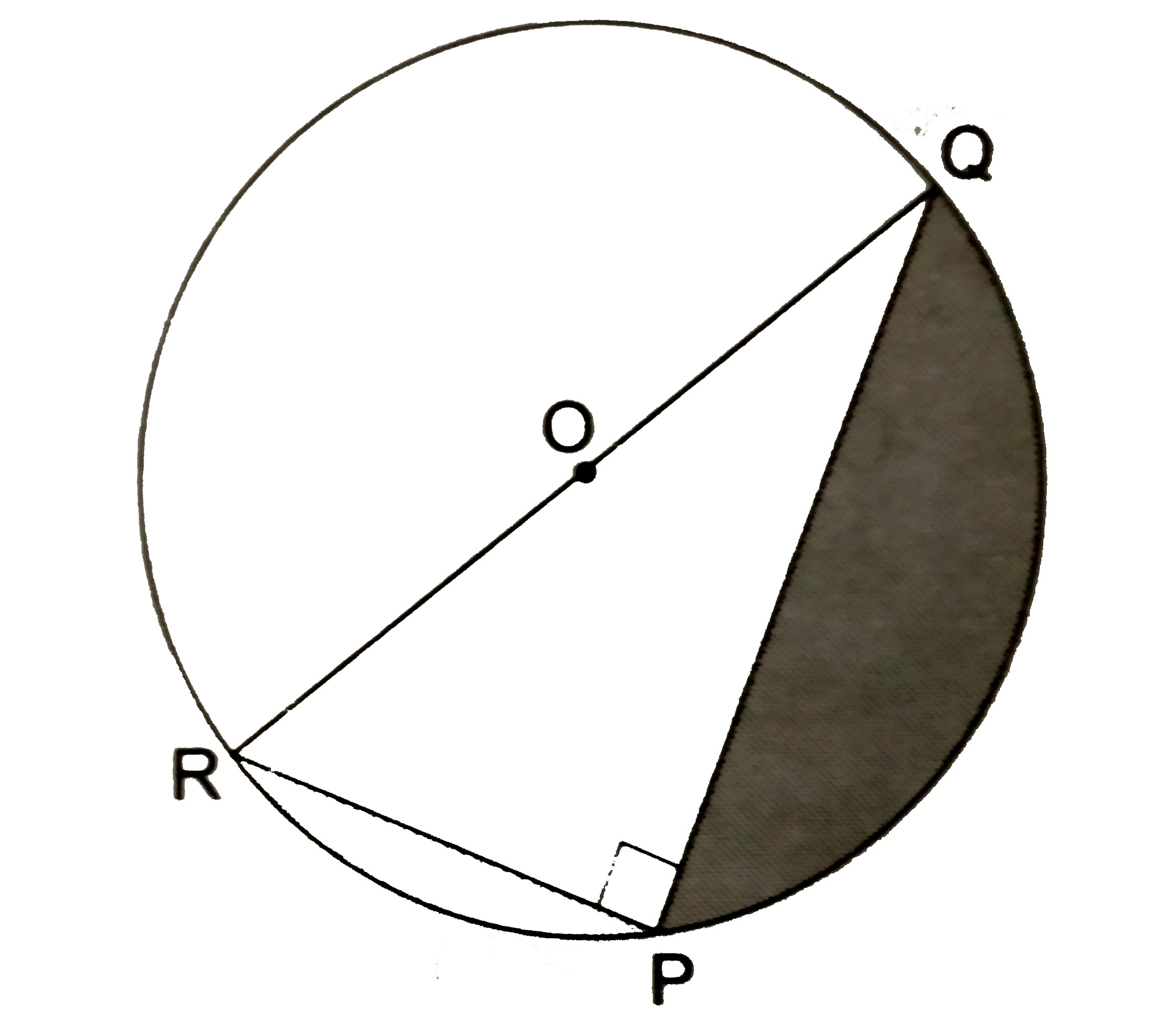
View SolutionIn the given figure, `DeltaABC` is right angled at A. Find the area of the shaded region if `AB=6cm, BC=10cm` and`O` is the centre of the incircle of `DeltaABC`. [Take `pi=3.14`]

View SolutionIn the given figure `Delta ABC` is right angled at A. Semicircles are drawn on AB, BC and AC as diameters. It is given that AB=3 cm and AC=4cm then find the area of the shaded region
View SolutionPQRS is a diameter of a circle of radius 6cm. The lengths PQ,QR and RS are equal. Semicircles are drawn with PQ and QS is diameters, as shown in the given figure. If `PS=12cm,` find the perimeter and area of the shaded region.

[Take `pi=3.14`]
View SolutionThe inside perimeter of a running track (shown in figure) is 400m. The length of each of the straight portion is 90m and the ends are semi-circles. If the track is everywhere 14m wide, find the area of the track. Also find the length of the outer running track.
View SolutionIn the given figure ABCD is a rectangle of dimensions `21cmxx14cm`. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure.

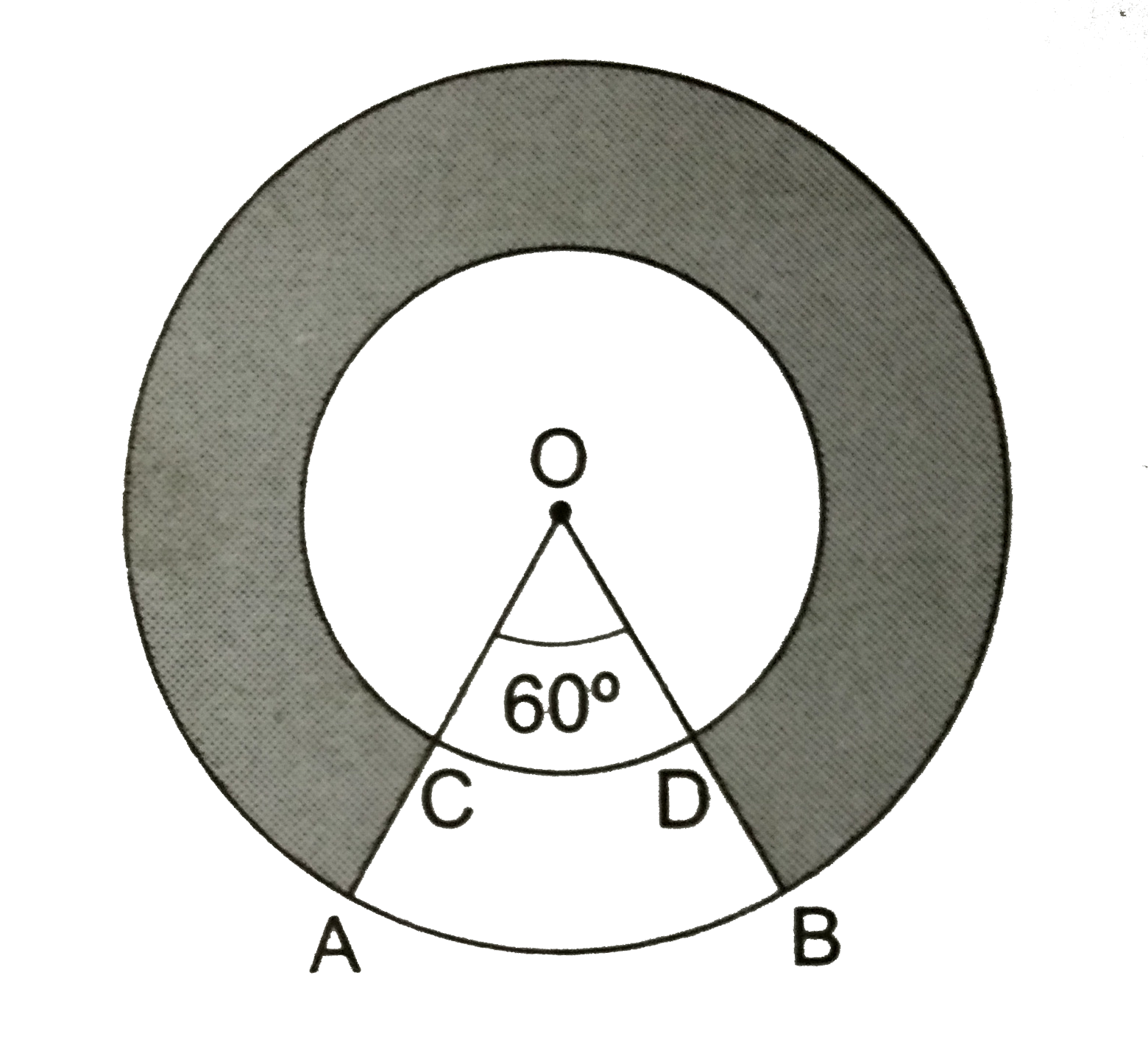
View SolutionIn the given figure, two concentric circles with centre O have radii 21 cm and 42 cm. If `/_AOB=60^(@)` find the area of the shaded region.
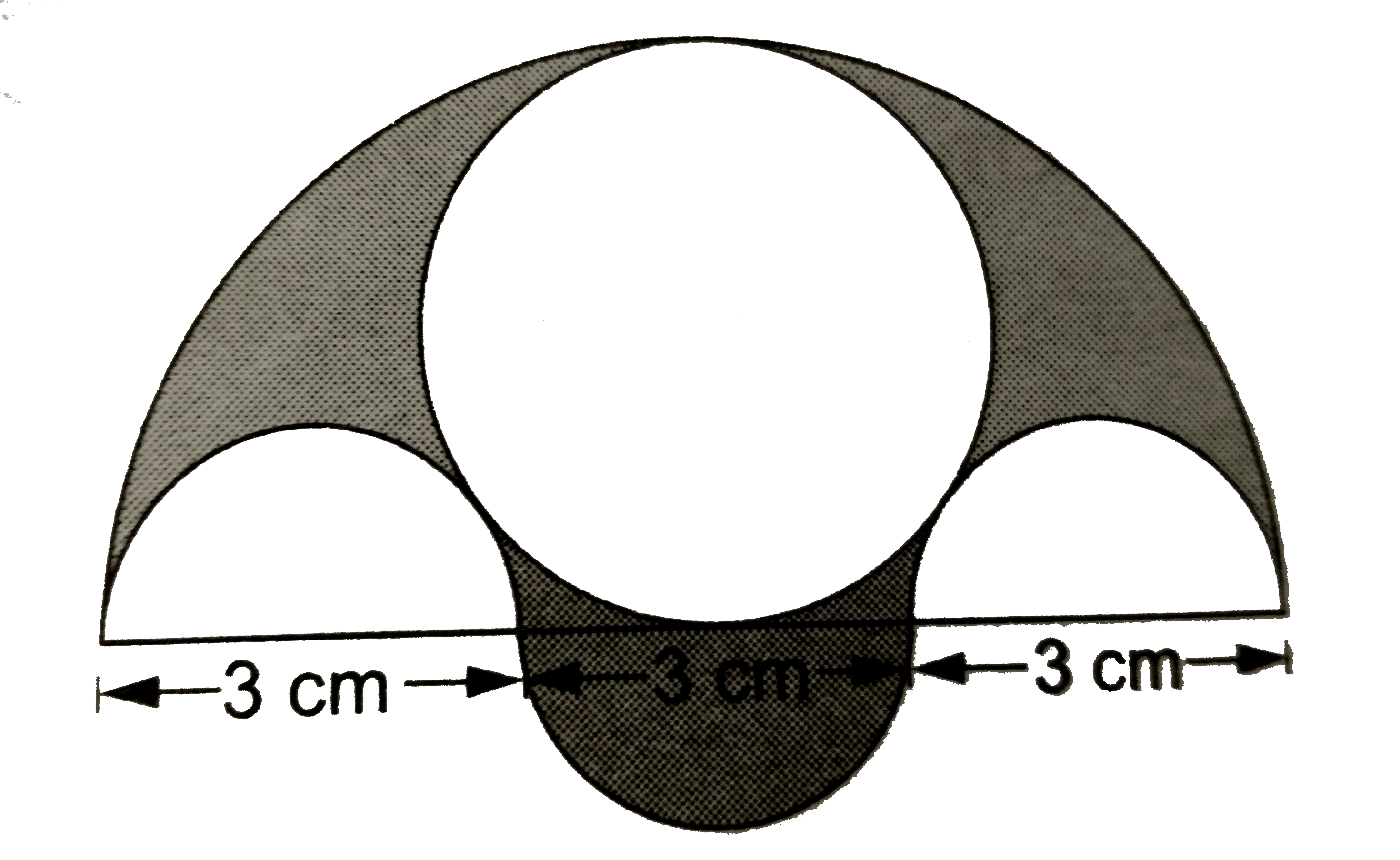
View SolutionThree semicirles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the given figure. Find the area of the shaded region.
View SolutionIn the given figure, the side of square is 28 cm and radius of each circle is half of the length of the sides of the square where O and O are centres of the circles. Find the area of shaded region
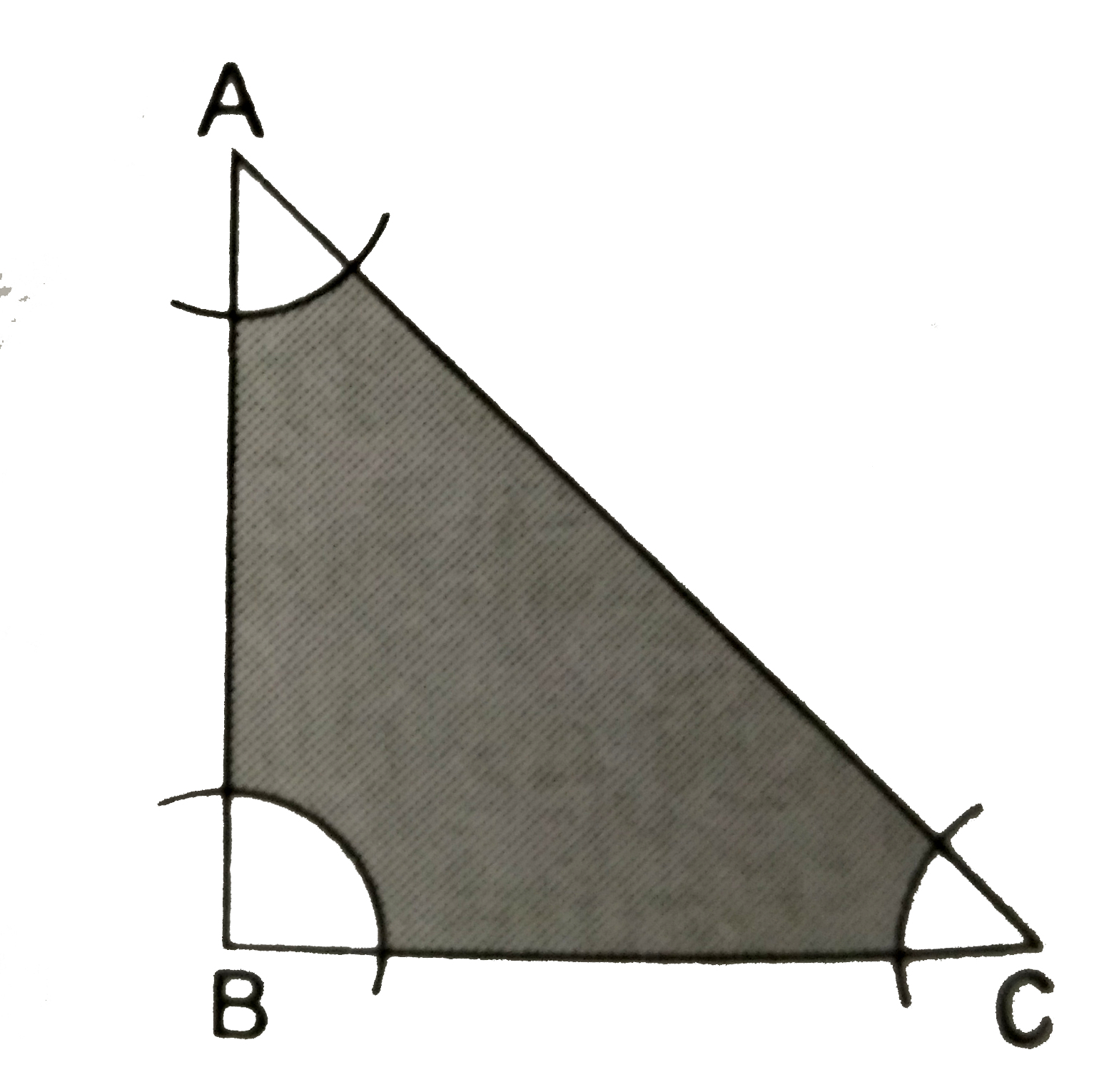
View SolutionWith the vertices A,B and C of a triangle ABC as centres, arcs are drawn with radii 5 cm each as shown in the given figure. If `AB=14cm, BC=48cm` and `CA=50cm` then find the area of the shaded region. [Use `pi=3.14`]
View SolutionIf the diameters of the concentric circles shown in the figure below are in the ratio `1:2:3` then find the ratio of the areas of three regions.

View Solution
Exercise 16A questions and complete solutions for chapter AREA OF CIRCLE, SECTOR AND SEGMENT of RS AGGARWAL MATHS (HINGLISH) of Class 10