Complete Solutions to HOTS (High Order Thinking Skills) of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| VK GLOBAL PUBLICATION | HOTS (High Order Thinking Skills) |
| Number Of Questions | 7 |
| Academic Year | 2023-24 |
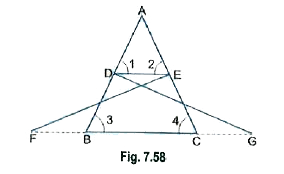
In Fig. 7.58, `DeltaFECequivDeltaGDB` and `angle1 = angle2`. Prove that `DeltaADE ~ DeltaABC`.
View SolutionSides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that`DeltaA B C DeltaP Q R`.
View SolutionIn figure, `P` is the mid-point of `B C ,Q` is the mid-point of `B C ,Q` is the mid-point of `A P` , such that `B Q` produced meets `A C` at `Rdot`
View SolutionIn figure ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that `(a r(A B C))/(a r(D B C))=(A O)/(D O)`.
View SolutionTwo poles of height a metres and `b` metres are `p` metres apart. Prove that the height of the point of intersection of the lines joining the top of each pole to the foot of the opposite pole is given by `(a b)/(a+b)` metres.
View SolutionIn an equilateral triangle ABC, D is a point on side BC such that `B D=1/3B C`. Prove that `9A D^2=7A B^2`.
View SolutionThrough the mid-point `M` of the side `C D` of a parallelogram `A B C D` , the line `B M` is drawn intersecting `A C` at `La n dA D` produced at `E` . Prove that `E L=2B Ldot`
View Solution
HOTS (High Order Thinking Skills) questions and complete solutions for chapter TRIANGLES of VK GLOBAL PUBLICATION MATHS (HINGLISH) of Class 10