Complete Solutions to PROFICIENCY EXERCISE (SHORT ANSWER TYPE QUESTIONS-II) of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| VK GLOBAL PUBLICATION | PROFICIENCY EXERCISE (SHORT ANSWER TYPE QUESTIONS-II) |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
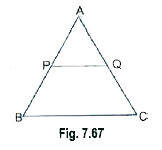
View Solution`PQabs()BC` and AP:PB = 1 : 2 find `("area"(DeltaAPQ))/("area"(DeltaABC))`.
View Solution`(OA)/(OC)=(OD)/(OB)`. Prove that `angleA= angleC` and `angleB= angleD`.
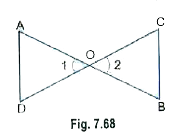
View SolutionSides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
(i) 13 cm, 12 cm, 5 cm (ii) 20 cm, 25 cm, 30 cm.
View SolutionIn `DeltaABC, DEabs()BC`. If AD= 4 cm, DB = 4.5cm and AE = 8cm, find AC.
View Solution` A B C` and `B D E` are two equilateral triangles such that `D` is the mid-point of `B C` . The ratio of the areas of the triangles `A B C` and `B D E` is `2:1` (b) `1:2` (c) `4:1` (d) `1:4`
View SolutionIn the given figure, AD is the bisector of `angle BAC`. If AB =10 cm , AC=6 cm and BC=12 cm, find BD and DC .
View SolutionThe perimeters of two similar triangles ABC and PQR are 60 cm and 36 cm respectively. If PQ = 9 cm, then find the length of AB.
View SolutionTwo poles of height 9 m and 15 m stand vertically upright on a plane ground. If the distance between their tops is 10m, then find the distance between their feet.
View SolutionThe area of two similar triangles PQR and XYZ are `144 cm^(2)` and `49 cm^(2)` respectively. If the shortest side of larger `DeltaPQR` be 24 cm, then find the shortest side of the smaller triangle XYZ.
View Solution`DeltaABC ~DeltaDEF`. If AB= 4cm,BC = 3.5cm,CA = 2.5cmandDF = 7.5cm, then find perimeter of `DeltaDEF`.
View SolutionIn `DeltaABC, DEabs()BC`. If AD= 2.4 cm, AE= 3.2 cm, DE= 2 cm and BC= 5 cm, find BD and CE.
View SolutionIn the given figure, in `DeltaABC, DE||BC` so that AD= (4x - 3) cm, AE= ( 8x-7) cm, BD= (3x-1) cm and CE= (5x-3) cm . Find the value of x.
View SolutionIf a line intersects sides AB and AC of a `DeltaA B C`at D and E respectively and is parallel to BC, prove that `(A D)/(A B)=(A E)/(A C)`
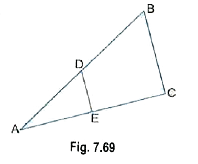
View SolutionIn Fig. 7.69, `DEabs()BC`. If `(AE)/(EC)=4/13` and AB= 20.4 cm, find AD.
View SolutionABCD is a trapezium in which ABIIDC and P and Qare points on AD and BC respectively such that `PQabs()DC`. If PD= 12 cm, BQ = 42 cm and QC = 18cm, find AD.
View SolutionThe Hypotenuse of a right triangle is 25 cm and out of the remaining two sides, one is larger than the other by 5 cm, find the lenghts of the other two sides.
View SolutionFor going to a city B from city A there is a route via city C such that `AC botCB`, AC =2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at the point O such that `(A O)/(B O)=(C O)/(D O)`. Show that ABCD is a trapezium.
View SolutionA street light bulb is fixed on a pole 6 m above the level of the street. If a women of height 1.5 m casts a shadow of 3 m, then find how far she is away from the base of the pole.
View SolutionIn Fig.7.70, find `angleE`.
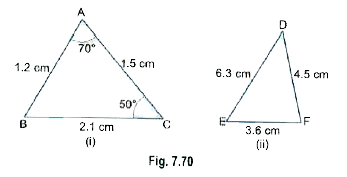
View SolutionD, E and F are respectively the mid-points of sides AB. BC and CA of`DeltaA B C` . Find the ratio of the areas of DDEF and`DeltaA B C` .
View SolutionA 15 high tower casts a sshadow 24 long at a certain time at the same time, a telephone pole casts a shadow 16 long. Find the height of the telephone pole.
View SolutionProve that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
View SolutionIn Fig. 3, ABC is a right triangle, right angled at C and D is the mid-point of BC. Prove that `AB^2 = 4AD^2 - 3AC^2`.
View SolutionIn Fig, ABC is an isosceles triangle in which AB= AC.Eis a point on the side CB produced such that `FEbotAC`. If `ADbotCB`, prove that `AB xx EF = AD xx EC`.

View Solution`A D` is an altitude of an equilateral triangle `A B Cdot` On `A D` as base, another equilateral triangle `A D E` is constructed. Prove that Area `( A D E):` Area `( A B C)=3: 4.`
View SolutionIn figure, `P` is the mid-point of `B C ,Q` is the mid-point of `B C ,Q` is the mid-point of `A P` , such that `B Q` produced meets `A C` at `Rdot`
View Solution`AB botBC` and `DE bot AC`. Prove that `DeltaABC ~ DeltaAED`.
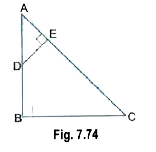
View SolutionTwo triangles `B A Ca n dB D C` , right angled at `Aa n dD` respectively, are drawn on the same base `B C` and on the same side of `B C` . If `A C` and `D B` intersect at `P ,` prove that `A PxP C=D PxP Bdot`
View Solution`E` is a point on side `A D` produced of a parallelogram `A B C D` and `B E` intersects `C D` at `F` . Prove that `D\ A B E D\ C F B` .
View SolutionD and E are respectively the points on the sides AB and AC of a triangle ABC such that AE = 5 cm, AC= 7.5 cm, DE= 4.2 cm and `DEabs() BC`. Then find length of BC.
View SolutionIf ABC is an equilateral triangle with each side a cm such that `ADbotBC`, then find `AD^(2)`.
View SolutionIn ` A B C ,\ \ D E` is parallel to base `B C` , with `D` on `A B` and `E` on `A C` . If `(A D)/(D B)=2/3` , find `(B C)/(D E)` .
View SolutionIf E is a point on side r:A of an equilateral triangle ABC such that `BE bot CA`, then prove that `AB^(2) +BC^(2) +CA^(2) = 4BE^(2)`.
View SolutionO is any point inside a rectangle ABCD. Prove that `O B^2+O D^2=O A^2+O C^2`.
View SolutionIn the given figure, `(AD)/(DB)=(AE)/(EC) and angle ADE=angleACB`. Prove that `Delta ABC` is an isosceles triangle.
View SolutionIn Fig. 4.72, `A B C D` . If `O A=3x-19 ,\ \ O B=x-4` , `O C=x-3` and `O D=4` , find `x` . (FIGURE)
View Solution`A B C` is a triangle and `P Q` is a straight line meeting `A B` in `P` and `A C` in `Q` . If `A P=1c m` , `P B=3c m` , `A Q=1. 5 c m` , `Q C=4. 5 m` , prove that area of ` A P Q` is one-sixteenth of the area of ` A B C` .
View Solution
PROFICIENCY EXERCISE (SHORT ANSWER TYPE QUESTIONS-II) questions and complete solutions for chapter TRIANGLES of VK GLOBAL PUBLICATION MATHS (HINGLISH) of Class 10