Complete Solutions to LONG ANSWER QUESTIONS of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| VK GLOBAL PUBLICATION | LONG ANSWER QUESTIONS |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
The line drawn from the midpoint of one side of a triangle parallel to another side bisects the third side.
View SolutionABCD is a trapezium in which AB||DC and its diagonals intersect each other at the point O. Show that `(A O)/(B O)=(C O)/(D O)`.
View SolutionIf AD and PM are medians of triangles ABC and PQR, respectively where`DeltaA B C DeltaP Q R`, prove that `(A B)/(P Q)=(A D)/(P M)`
View SolutionIn Fig. 4.123, ABCD is a trapezium with `AB || DC`. If `Delta AED` is similar to `Delta BEC`, prove that `AD= BC`.
View SolutionProve that the area of an equilateral triangle described on a side of a right-angled isosceles triangle is half the area of the equilateral triangle described on its hypotenuse.
View SolutionIf the areas of two similar triangles are equal, prove that they are congruent.
View SolutionThe areas of the two similar triangles are in the ratio of the square of the corresponding medians.
View SolutionO is the a point in the interior of `Delta ABC, OD bot BC, OE bot AC and AC and OF bot AB`, as shown in the figure,
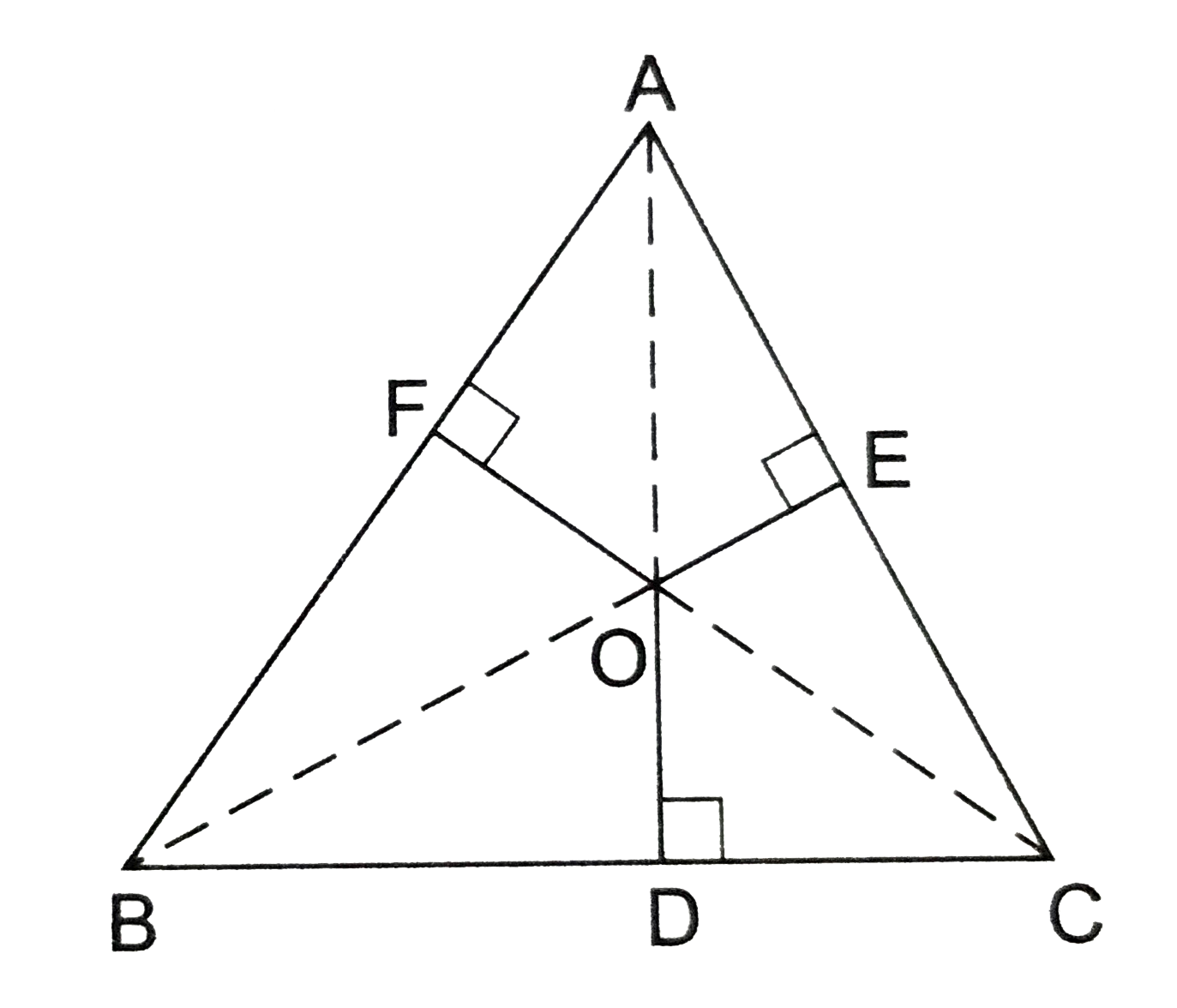
Prove that :
`(i) OA^(2)+OB^(2)+OC^(2)-OD^(2)-OD^(2)-OF^(2)=AF^(2)+BD^(2)+CE^(2)`
(ii) `AF^(2)+BD^(2)+CE^(2)=AD^(2)+BF^(2)+CD^(2)`
View SolutionThe perpendicular from A on side BC of a ABC intersects BC at D such that DB = 3 CD. Prove that `2AB^2 = 2AC^2 + BC^2`.
View SolutionIn an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
View SolutionProve that, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Using the above result, do the following:
In Fig. 7 .45 `DE abs() BC` and BD = CE. Prove that `DeltaABC` is an isosceles triangle.
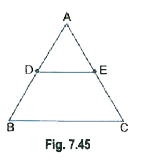
View Solution`In DeltaABC A = 90^@ and AC _|_ BD`, then Show that` (a) AB^2=BC.BD (b) AC^2= BC.DC (c) AD^2=BD.CD`
View SolutionDiagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
View SolutionProve that, in a right triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides. Using the above, do the following:
Prove that, in a `DeltaABC`, if AD is perpendicular to BC, dien `AB^(2) + CD^(2) = AC^(2) + BD^(2)`.
View SolutionIn a triangle, if the square on one side is equal to the sum of the squares on the other two sides, prove that the angle opposite to the first side is a right angle. Use the above theorem to find the measure of `anglePKR` in Fig. 7.52.

View SolutionABC is a triangle in which `AB = AC and D` is a point on AC such that `BC^2 = AC xx CD`.Prove that `BD = BC`.
View SolutionProve that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
View SolutionD and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that `A E^2+B D^2=A B^2+D E^2`.
View Solution
LONG ANSWER QUESTIONS questions and complete solutions for chapter TRIANGLES of VK GLOBAL PUBLICATION MATHS (HINGLISH) of Class 10