Complete Solutions to ILLUSTRATIVE EXAMPLES of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| ZEN PUBLICATION | ILLUSTRATIVE EXAMPLES |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
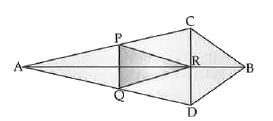
In the figure, `PR || RC` and `QR || BD`. Prove that `PQ || CD`.
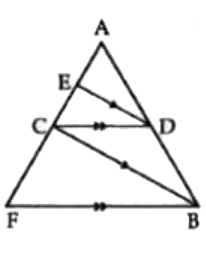
View SolutionIn the given figure `DE||BCandCD||BF` prove that `AC^(2)=AExxAF`.
View SolutionIn the figure, `AB_|_BCandDE_|_AC`. Prove that `DeltaABC~DeltaAED`.

View SolutionIn the given figure P is the midpoint of BC and Q is the midpoint of AP. If BQ when produced meets AC at R, prove that `RA=1/3CA`.

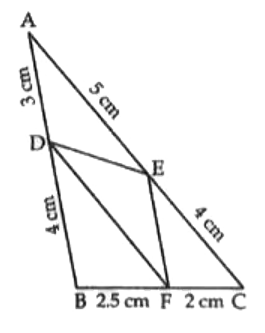
View SolutionIn the given figure, AD = 3 cm, AE = 5 cm, BD = 4 cm, CE = 4 cm, CF = 2 cm, BF = 2.5 cm, then find the pair of parallel lines and hence their lengths.
View SolutionIn the `DeltaABC`, altitudes AD and CE intersect each other at point P. Prove that

i] `DeltaAPE~DeltaCPD`
ii] `APxxPD=CPxxPE`
iii] `DeltaADB~DeltaCEB`
iv] `ABxxCE=BCxxAD`
View SolutionIn the figure `lfloorQPR=lfloorUTS=90^(@)andPR||TS`. Prove that `DeltaPQR~DeltaTUS`.

View SolutionIn the figure `(AO)/(OC)=(BO)/(OD)=1/2` and AB = 5 cm. Find DC

View SolutionIf the area of two similar triangles is in the ratio 25 : 64, find the of their corresponding sides.
View SolutionD, E and F are the mid-points of sides of `Delta ABC`. P, Q, R are the mid-points of sides DEF. This process of marking the mid-points and forming a new triangle is continued. How are the areas of these triangles related?
View SolutionIn areas of two similar triangles ABC and PQR are in the ratio 9 : 16. If BC = 4.5 cm. Find the length of QR.
View Solution`Delta ABC` and `Delta BDE` are two equilateral triangles and `BD = DC`. Find the ratio between areas of `Delta ABC` and `Delta BDE`.
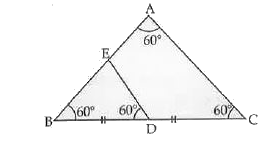
View SolutionAD is altitude of equilateral `DeltaABC`. On AD as base, another equilateral triangle ADE is constructed. Prove that `("Area of "DeltaADE)/("Area of "DeltaABC)=3/4`.

View SolutionThe lengths of diagonals of a rhombus are 24 cm and 32 cm. Calculate the altitide of the rhombus.

View SolutionThe sides AB and AC and the perimeter `P_(1)` of `DeltaABC` are respectively three times the corresponding sides DE and DF and the perimeter `P_(2)` of `DeltaDEF`. Are the two triangles similar? If yes, find `(ar(DeltaABC))/(ar(DeltaDEF))`.
View SolutionIn the rectangle WXYZ, XY + YZ = 17 cm and XZ + YW = 26. Calculate the length and breadth of the rectangle.

View SolutionAn insect 8 m away from the foot of a lamp post 6 m tall, crawls towards it. After moving through a distance, its distance from the top of the lamp post is equal to the distance it has moved. How far is the insect away from the foot of the lamp post?
View SolutionIn `Delta ABC`, C is a point on BD such that BC:CD=1:2 and △ABC is an equilateral triangle Prove that `AD^(2) = 7AC^(2)`
View SolutionIn `DeltaABC,CD_|_AB,CA=2AD,BD=3AD`. Prove that `lfloorBCA=90^(@)`.

View SolutionIn the figure, `AB_|_BCandDE_|_AC`. Prove that `DeltaABC~DeltaAED`.

View SolutionIn the given figure `lfloorBAC=90^(@)`.
Prove that :

a] `DeltaAGF~DeltaBDG`
b] `DeltaAGF~DeltaEFC`
c] `DeltaBDG~DeltaEFC`
d] `DE^(2)=BDxxEC`
View SolutionABC is a right angled triangle. Points D and E trisect BC. Prove that `8AE^(2)=3AC^(2)+5AD^(2)`.

View SolutionIn an equilateral triangle ABC, `AD_|_BC`. Prove that `AD^(2)=3BD^(2)`.

View Solution
ILLUSTRATIVE EXAMPLES questions and complete solutions for chapter TRIANGLES of ZEN MATHS (KANNADA ENGLISH) of Class 10
All Exercises from ZEN PUBLICATION Class 10 MATHS TRIANGLES
- ILLUSTRATIVE EXAMPLES
- TEXTUAL EXERCISES (EXERCISE 2.1)
- TEXTUAL EXERCISES (EXERCISE 2.2)
- TEXTUAL EXERCISES (EXERCISE 2.3)
- TEXTUAL EXERCISES (EXERCISE 2.4)
- TEXTUAL EXERCISES (EXERCISE 2.5)
- ZEE ADDITIONAL QUESTIONS - LONG ANSWER TYPE QUESTIONS
- ZEE ADDITIONAL QUESTIONS - SHORT ANSWER TYPE - 1 QUESTIONS
- ZEE ADDITIONAL QUESTIONS - SHORT ANSWER TYPE - 2 QUESTIONS
- ZEE ADDITIONAL QUESTIONS - VERY SHORT ANSWER QUESTIONS
- ZEE ADDITIONAL QUESTIONS -MULTIPLE-CHOICE QUESTIONS