Complete Solutions to TEXTUAL EXERCISES (EXERCISE 2.5) of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| ZEN PUBLICATION | TEXTUAL EXERCISES (EXERCISE 2.5) |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
Sides of triangles are given below. Determine which of them are right triangles.
In case of a right triangle , write the length of its hypotenuse.
7cm, 24 cm, 25 cm
View SolutionPQR is a triangle right angled at P and M is a point on QR such that `PM_|_QR`. Show that `PM^(2)=QM.MR`.

View SolutionIn the figure ABD is a triangle right-angled at A and `AC_|_BD`. Show that
i] `AB^(2)=BC.BD`
ii] `AC^(2)=BC.DC`
iii] `AD^(2)=BD.CD`

View SolutionABC is an isosceles triangle right-angled at C. Prove that `AB^(2)=2AC^(2)`.

View SolutionABC is an isosceles triangle with AC = BC. If `AB^(2)=2AC^(2)`, prove that ABC is a right-angled triangle.

View SolutionABC is an equilateral triangle of side 2a. Find each of its altitudes.

View SolutionProve that sum of the squares of the side of a rhombus is equal to the to the sum of the squares of its diagonals.
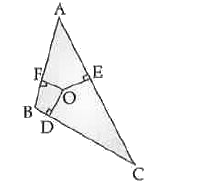
View SolutionIn the figure given below, `O` is point in the interior of a triangle ABC, `OD _|_ BC`, `OE _|_ AC` and `OF _|_ AB`. Show that
(i) `OA^(2) + OB^(2) + OC^(2) + OD^(2) - OE^(2) - OF^(2) = AR^(2) + BD^(2) + CE^(2)`
(ii) `AF^(2) + BD^(2) + CE^(2) = AE^(2) + CD^(2) + BF^(2)`
View SolutionA ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
View SolutionA guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end . How far from the base of the pole should the stake be driven so that the wire will be taut ?
View SolutionAn aeroplane leaves an airport and files due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airpot and flies due west at a speed of 1200 km per hour . How far apart will be the two planes after `1(1)/(2)` hours ?
View SolutionTwo poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12m , find the distance between their tops .
View SolutionD and E are points on the sides CA and CB respectively of a triangle ABC right angale at C. prove that `AE^(2)+BD^(2)=AB^(2)+DE^(2).`
View SolutionThe perpendicular from A on side BC of a `DeltaABC` intersects BC at D such that DB = 3CD. Prove that `2AB^(2)=2AC^(2)+BC^(2)`.

View SolutionIn an equilateral triangle ABC, D is a point on BC such that `BD=1/3BC`. Prove that `9AD^(2)=7AB^(2)`.

View SolutionIn an equilateral triangle prove that three times the square of one side is four times the square of its altitude.

View SolutionTick the correct answer and justify : In `DeltaABC,AB=6sqrt3cm, AC=12 cm and BC=6cm`
The angle B is :
View Solution
TEXTUAL EXERCISES (EXERCISE 2.5) questions and complete solutions for chapter TRIANGLES of ZEN MATHS (KANNADA ENGLISH) of Class 10
All Exercises from ZEN PUBLICATION Class 10 MATHS TRIANGLES
- ILLUSTRATIVE EXAMPLES
- TEXTUAL EXERCISES (EXERCISE 2.1)
- TEXTUAL EXERCISES (EXERCISE 2.2)
- TEXTUAL EXERCISES (EXERCISE 2.3)
- TEXTUAL EXERCISES (EXERCISE 2.4)
- TEXTUAL EXERCISES (EXERCISE 2.5)
- ZEE ADDITIONAL QUESTIONS - LONG ANSWER TYPE QUESTIONS
- ZEE ADDITIONAL QUESTIONS - SHORT ANSWER TYPE - 1 QUESTIONS
- ZEE ADDITIONAL QUESTIONS - SHORT ANSWER TYPE - 2 QUESTIONS
- ZEE ADDITIONAL QUESTIONS - VERY SHORT ANSWER QUESTIONS
- ZEE ADDITIONAL QUESTIONS -MULTIPLE-CHOICE QUESTIONS