Complete Solutions to ZEE ADDITIONAL QUESTIONS - LONG ANSWER TYPE QUESTIONS of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| ZEN PUBLICATION | ZEE ADDITIONAL QUESTIONS - LONG ANSWER TYPE QUESTIONS |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
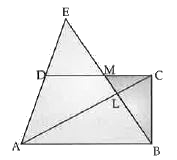
Throught the mid-point M of the sides of a parallelogram ABCD, the line BM is drawn intersecting AC at L, and AD produced to E. Prove that `EL = 2 BL`.
View SolutionA 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, find the distance by which the top of the ladder would slide upwards on the wall.
View SolutionIn the figure, OB is the perpendicular bisector of the line segment DE. `FA_|_OB` and FE intersects OB at point C. Prove that `1/(OA)+1/(OB)=2/(OC)`.

View SolutionIn triangle ABC, AP, BQ and CR are the medians. Prove that `3[AB^(2)+BC^(2)+AC^(2)]=4[AP^(2)+BQ^(2)+CR^(2)]`.

View SolutionIf A is the area of a right angled triangle and b is one of the sides containing the right angle. Prove that the length of the altitude on the hypotenuse is `(2Ab)/(sqrt(b^(4)+4A^(2)))`.

View SolutionIn the given figure, AD is the median of `DeltaABCandAE_|_BC`. Prove that : `b^(2)+c^(2)=2p^(2)+1/2a^(2)`.

View SolutionIn an equilateral triangle ABC, D is a point of BC such that 4BD = BC. Prove that `16AD^(2)=13BC^(2)`.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionIn a right angled triangle, square on the hypotenuse is equal to sum of the squares on the other sides. Prove the statement.
View SolutionState and prove pythagoras theorem .
View Solution
ZEE ADDITIONAL QUESTIONS - LONG ANSWER TYPE QUESTIONS questions and complete solutions for chapter TRIANGLES of ZEN MATHS (KANNADA ENGLISH) of Class 10
All Exercises from ZEN PUBLICATION Class 10 MATHS TRIANGLES
- ILLUSTRATIVE EXAMPLES
- TEXTUAL EXERCISES (EXERCISE 2.1)
- TEXTUAL EXERCISES (EXERCISE 2.2)
- TEXTUAL EXERCISES (EXERCISE 2.3)
- TEXTUAL EXERCISES (EXERCISE 2.4)
- TEXTUAL EXERCISES (EXERCISE 2.5)
- ZEE ADDITIONAL QUESTIONS - LONG ANSWER TYPE QUESTIONS
- ZEE ADDITIONAL QUESTIONS - SHORT ANSWER TYPE - 1 QUESTIONS
- ZEE ADDITIONAL QUESTIONS - SHORT ANSWER TYPE - 2 QUESTIONS
- ZEE ADDITIONAL QUESTIONS - VERY SHORT ANSWER QUESTIONS
- ZEE ADDITIONAL QUESTIONS -MULTIPLE-CHOICE QUESTIONS