Complete Solutions to ZEE ADDITIONAL QUESTIONS - SHORT ANSWER TYPE - 1 QUESTIONS of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| ZEN PUBLICATION | ZEE ADDITIONAL QUESTIONS - SHORT ANSWER TYPE - 1 QUESTIONS |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
Legs of a right triangle are of lengths 16 cm and 8 cm. Find the length of the side of the largest square that can be inscribed in the triangle.
View SolutionIn the figure `lfloorD=lfloorEand(AD)/(DB)=(AE)/(EC)`. Prove that BAC is an isosceles triangle.

View SolutionDiagonals of trapezium PQRS intersect each other at the point O, PQ||RS, and PQ = 3RS. Find the ratio of the areas of triangles POQ and ROS.
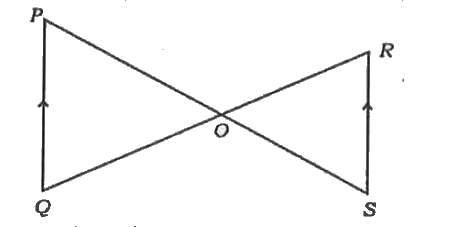
View SolutionIn the given figure PQ `||` RS , prove that `Delta POQ~Delta SOR.`
View SolutionIn the triangle PQR, is a point on PR such that `QN_|_PR`. If PN. NR = `QN^(2)`, prove that `lfloorPQR=90^(@)`.
View SolutionIf in a `DeltaPQR,XY||QR,PX=22x,XQ=3x,PY=x`, and YR = 9x, find the value of x.
View SolutionIn a rectangle ABCD, E is the mid point of AB. If AB = 16 cm and AD = 6 m, find ED.
View SolutionIn the given figure, `lfloorACB=90^(@)andCD_|_AB`. Prove that `(BC^(2))/(AC^(2))=(BD)/(AD)`.

View SolutionIn an isosceles `DeltaABC,AB=ACandBD_|_AC`. Prove that `BD^(2)-CD^(2)=2CD.AD`.
View SolutionIn a quadrilateral ABCD, `lfloorB=90^(@)`. If `AD^(2)=AB^(2)+BC^(2)+CD^(2)`, prove that `lfloorACD=90^(@)`.
View SolutionP and Q are the points on sides AB and AC respectively of `DeltaABC`. If AP = 3 cm, PB = 6 cm, AQ = 5 cm and QC = 10 cm, show that BC = 3 PQ.
View SolutionIn `Delta` ABC , AD `bot`BC and `AD^(2)= BD xx CD`. Prove that `AB^(2) + AC^(2)`= `(BD + CD)^(2)`

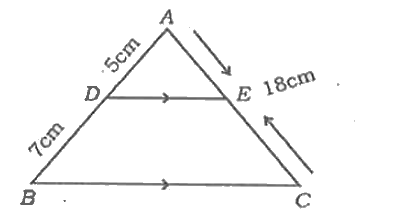
View SolutionIn `Delta` ABC , DE `||` BC . If AD= 5 cm , BD = 7 cm and AC = 18 cm , find the length of AE.
View Solution`Delta ABC~Delta DEF` and their areas are `64 cm^2 and 100 cm^2` respectively. If `EF=12 cm` then find the measure of BC.
View SolutionThe diagonal BD of parallelogram ABCD intersect AE at F as shown in the figure. If E is any point on BC, then prove that `DFxxEF=FB=FA`.
View Solution
ZEE ADDITIONAL QUESTIONS - SHORT ANSWER TYPE - 1 QUESTIONS questions and complete solutions for chapter TRIANGLES of ZEN MATHS (KANNADA ENGLISH) of Class 10
All Exercises from ZEN PUBLICATION Class 10 MATHS TRIANGLES
- ILLUSTRATIVE EXAMPLES
- TEXTUAL EXERCISES (EXERCISE 2.1)
- TEXTUAL EXERCISES (EXERCISE 2.2)
- TEXTUAL EXERCISES (EXERCISE 2.3)
- TEXTUAL EXERCISES (EXERCISE 2.4)
- TEXTUAL EXERCISES (EXERCISE 2.5)
- ZEE ADDITIONAL QUESTIONS - LONG ANSWER TYPE QUESTIONS
- ZEE ADDITIONAL QUESTIONS - SHORT ANSWER TYPE - 1 QUESTIONS
- ZEE ADDITIONAL QUESTIONS - SHORT ANSWER TYPE - 2 QUESTIONS
- ZEE ADDITIONAL QUESTIONS - VERY SHORT ANSWER QUESTIONS
- ZEE ADDITIONAL QUESTIONS -MULTIPLE-CHOICE QUESTIONS