Complete Solutions to Pressure Difference And Capillarity of chapter PROPERTIES OF MATTER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | PROPERTIES OF MATTER |
| A2Z | Pressure Difference And Capillarity |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
An open capillary tube is lowered in vessel with mercury. The difference between the levels of the mecury in the vessel and in the capillary tube `/_\h=4.6 mm`. What is the radius of curvature of the mercury meniscus in the capillary tube? Surface tension of mercury is `0.46N//m`, density of mercury is `13.6gm//"cc"`.
02:50View SolutionWater rises to a height of `10cm` in a glass capillary tube. If the area of cross section of the tube is reduced to one fourth of the former value what is the height of water rise now?
02:40View SolutionTwo spherical soap bubbles of radii `r_1` and `r_2` in vacuume collapse under isothermal condition. The resulting bubble has radius `R` such that
04:28View SolutionThe execc pressure inside the first soap bubble is three times that inside the second bubble. Then the ratio of the volumes of the first and second bubbles is
02:01View SolutionWhen a capillary tube is dipped in water, water rises upto `8cm` in the tube. What happends when the tube is pushed down such that its end is only `5cm` above outside water level?
02:48View SolutionThe excess pressure due to surface tension inside a spherical drop is `6 units`. If eight such drops combine, then the excess pressure due to surface tension inside the larger drop is
01:39View SolutionWater rise in capillary tube when its one end is dipped vertically in it, is 3 cm. If the surface tension of water is `75xx10^-3(N)/(m)`, then the diameter of capillary will be (Take angle of contact`=0^@C`)
02:28View SolutionA capillary tube of radius `r` is immersed in a liquid. The liquid rises to a height `h`. The corresponding mass is `m`. What mass of water shall rise in the capillary if the radius of the tube is doubled?
02:02View SolutionA capillary tube of radius 0.20 mm is dipped verticaly in water. Find the height of the water column raised in the tube. Surface tensionn of water `=0.075Nm^-1` and density of water `=1000 kgm^-3. Take g=10 ms^-2`.
02:41View SolutionTwo mercury drops each of radius r merge to form a bigger drop. Calculate the surface energy released.
06:19View SolutionA spherical drop of water as `1mm` radius. If the surface tension of the the water is `50xx10^-3(N)/(m)`, then the difference of pressure between inside and outside the spherical drop is:
00:58View SolutionA soap bubble of raidus `R` is surrounded by another soap bubble of radius `2R`, as shown. Take surface tension `=S`. Then the pressure inside the smaller soap bubble, in excess of the atmosphere presure will be
 01:30View Solution
01:30View SolutionA capillary tube of length
(i) `l = 60 cm`,
(ii) `l = 50 cm`
and radius `r = 1//4 mm` is immersed vertically into water. Find the capillary rise in both cases. Angle of contact `= 0^@`. Take coefficient of surface tension as `72 "dyne"//cm, g = 1000 cm s^(-2)`.03:17View SolutionA soap bubble is blown with the help of mechanical pump at the mouth of a tube. The pump produces a cartain increase per minute in the volume of the bubble, irrespective of its internal pressure. The graph between the pressure inside the soap bubble and time `t` will be
04:13View SolutionPressure inside two soap bubbles are `1.01` and `1.02` atmospheres. Ratio between their volumes is
02:15View SolutionIf pressure at half the depth of a lake is equal to 2//3 pressure at the bottom of the lake then what is the depth of the lake ?
01:51View SolutionThe pressure inside a small air bubble of radius `0.1`mm situated just below the surface of water will be equal to [Take surface tension of water `70xx10^-3Nm^-1` and atmospheric pressure`=1.013xx10^5Nm^-2`]
03:04View SolutionThe correct curve between the height or depression `h` of liquid in a capillary tube and its radius is
00:56View SolutionWater rises to a height of `16.3cm` in a capillary of height `18cm` above the water level. If the tube is cut at a height of `12cm`
03:07View Solution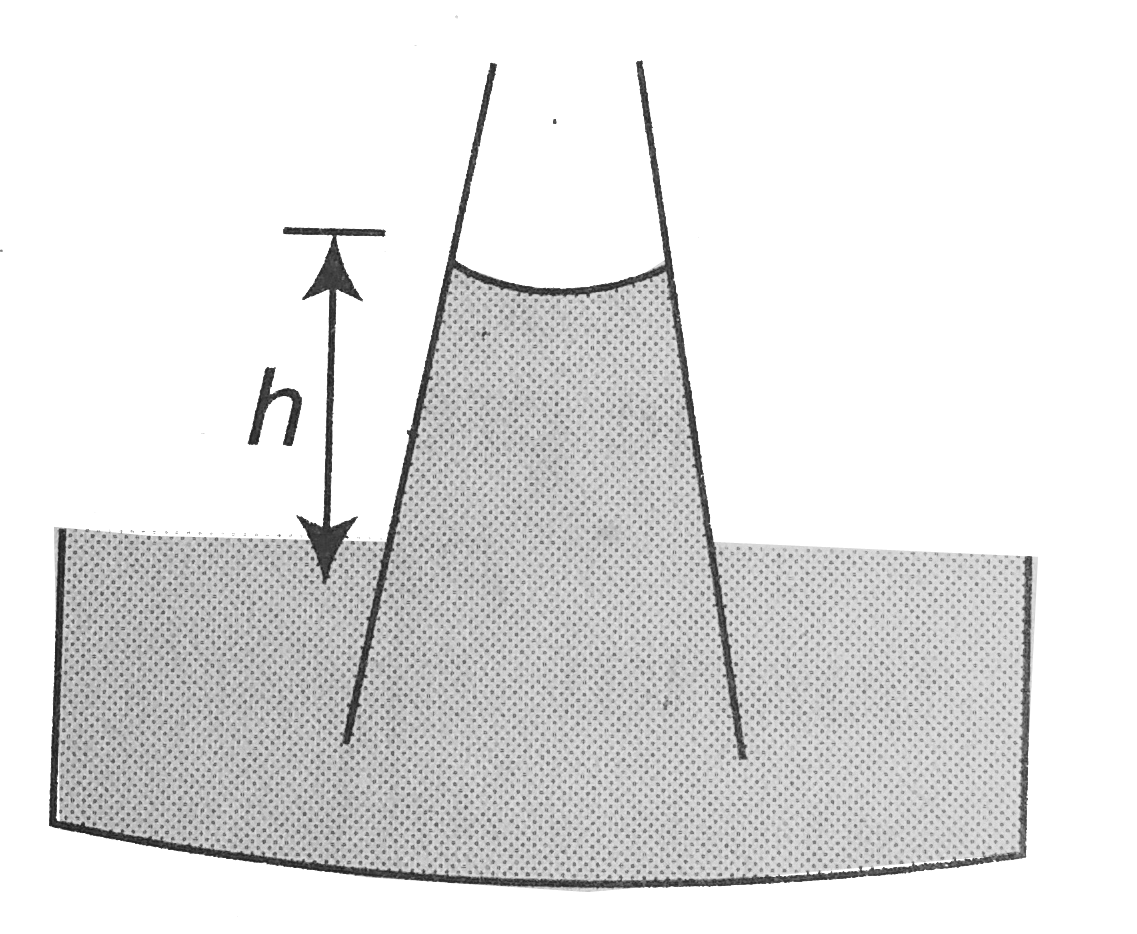
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is `0^@` and effect of liquid inside the mexiscus is to be neglected. `T` is surface tension of the liquid, `r` is radius of the meniscus, `g` is acceleration due to gravity and `rho` is density of the liquid then height `h` in equilibrium is:01:39View SolutionAssuming the xylem tissues through which water rises from root to the branches in a tree to be of uniform cross-section find the maximum radius of xylem tube in a `10m` high coconut tree so that water can rise to the top.
(Surface tension of water`=0.1(N)/(m)`, Angle of contact of water with xylem tube`=60^@`)01:56View SolutionWater rises to a height of `2 cm` in a capillary tube. If the tube is tilted `60^@` from the vertical, water will rise in the tube to a length of
04:59View SolutionWater rises in a capillary tube to a certain height such that the upward force due to surface tension is balanced by `75xx10^-4` newton force due to the weight of the liquid. If the surface tension of water is `6xx`10^-2` newton/metre the inner circumference of the capillary must be:
02:12View Solution
Pressure Difference And Capillarity questions and complete solutions for chapter PROPERTIES OF MATTER of A2Z PHYSICS (HINGLISH) of Class 11
