Complete Solutions to Viscosity of chapter PROPERTIES OF MATTER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | PROPERTIES OF MATTER |
| A2Z | Viscosity |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
When the temperature increases the viscosity of
View SolutionEight drops of water, each of radius `2mm` are falling through air at a terminal velcity of `8cms^-1`. If they coalesce to form a single drop, then the terminal velocity of combined drop will be
View SolutionA metal plate of area `2m^2` is pulled horizontally with a velocity of `0.5m^-1` on a liquid layer `1mm` thick. The force required, if the viscosity of liquid is `12Nsm^-2` is
View SolutionFind the minimum force required to drag a hard polythene plate of area `2 m^(2)` on a thin film of oil of thickness `0.25 cm` and `eta= 15` poise. Assume the speed of the plate is `10 cm s^(-1)`.
View SolutionA force of `3.14 N` is required to drag a sphere of radius `4 cm` with a speed of `5 ms^(-1)` in a medium in gravity free space. Find the coefficient of the viscosity of the medium.
View Solution
A space `2.5cm` wide between two large plane surfaces is filled with oil. Force required to drag a very thin plate of area `0.5m^2` just midway the surfaces at a speed of `0.5(m)/(sec)` is `1N`. The coefficient of viscosity in `kg-(s)/(m^2)` is:
View SolutionA rain drop radius `0.3mm` falling vertically downwards in air has a terminal velocity of `1(m)/(s)` The viscosity of air is `18xx10^-5` poise. The viscous force on the drop is
View SolutionA copper ball of radius `r` is moving with a uniform velocity `u` in the mustard oil. The dragging force acting on the ball is `F`. The dragging force on the copper ball of radius `2r` moving with uniform velocity `2u` in the mustart oil is
View SolutionA small steel ball of mass `m` and radius `r` is falling under gravity through a viscous liquid of coefficient of viscosity `eta`. If `g` is the value of acceleration due to gravity. Then the terminal velocity of the ball is proportional to (ignore buoyancy)
View SolutionA small steel ball falls through a syrup at a constant speed of `10cms^-1`. If the steel ball is pulled upwards with a force equal to twice its effective weight, how fast will it move upwards?
View SolutionAn air bubble of 1 cm radius is rising at a steady rate of `2.00ms^-1` through a liquid of density `1.5gcm^-3`. Neglect density of air. If `g=1000cms^-2`, then the coeffieciet of viscosity of the liquid is
View SolutionTwo indetical spherical drops of water are falling (vertically downwards) through air with a steady velocity of `5(cm)/(sec)`. If both the drops coalesce (combine) to form a new spherical drop, the terminal velocity of the new drop will be (neglect buoyant force on the drops.)
View SolutionUniform speed of 2 cm diameter ball is `20cm//s` in a viscous liquid. Then, the speed of 1 cm diameter ball in the same liquid is
View SolutionCoefficient of vilocity of water `=0.01` poise, density of water `=1 g cm ^(-3)`. Then the maximum velocity with which water can flow through a capillary tube of radius `0.05 cm`, without turbulent flow setting in, is
View SolutionA metal ball `B_(1)` (density `3.2g//"cc")` is dropped in water, while another metal ball `B_(2)` (density `6.0g//"cc")` is dropped in a liquid of density `1.6g//"cc"`. If both the balls have the same diameter and attain the same terminal velocity, the ratio of viscosity of water to that of the liquid is
View SolutionA rain drop starts falling from a height of `2km`. If falls with a continuously decreasing acceleration and attains its terminal velocity at a height of `1km`. The ratio of the work done by the gravitational force in the first halt to that in the second half of the drops journey is
View SolutionA drop of water of radius `0.0015 mm` is falling in air. If the coefficient of viscosity of air is `1.8 xx 10^(-3)kg//m^(3)`, what will be the terminal velocity of the drop? Density of water `= 1.0 xx 10^(3) kg//m^(3)` and `g = 9.8 N//kg`. Density of air can be neglected.
View SolutionA metallic sphere of radius `1.0 xx 10^(-3) m` and density `1.0 xx 10^(4) kg//m^(3)` enters a tank of water, after a free fall through a distance of h in the earth's gravitational field. If its velocity remains unchanged after entering water, determine the value of `h`. Given: coefficient of viscosity of water `= 1.0 xx 10^(-3) N s//m^(2), g = 10ms^(-2)` and density of water `= 1.0 xx 10^(3) kg//m^(3)`.
View SolutionConsider the following statements:
(i) Young's modulus is numerically equal to the stress which will double the length of a wire.
(ii) Viscosity of gases is greater than that of liquids.
(iii) The surface tension of a liquid decreases due to the presence of insoluble contamination.
The number of above statements that are true is
View Solution
The diagram shows a cup of tea seen from above. The tea has been stirred and is now rotating without turbulence. A graph showing the speed `v` with which the liquid is crossing points at a distance `X` from `O` along a radius `OX` would took like
View SolutionA tall cylinder is filled with viscous oil. A round pebble is dropped from the top with zero initial velocity. From the plot shown in figure, indicate the one that represents the velocity `(v)` of the pebble as a function of time `(t)`
View SolutionA ball is thrown vetically upwards at time `t=0`. Air resistance is not negligible and the acceleration of free fall is `g`. The ball reaches a maximum height at time `t=T` and then descends, reaching terminal speed. Which graph best shows the variation with time `t` to the acceleration a of the ball
View Solution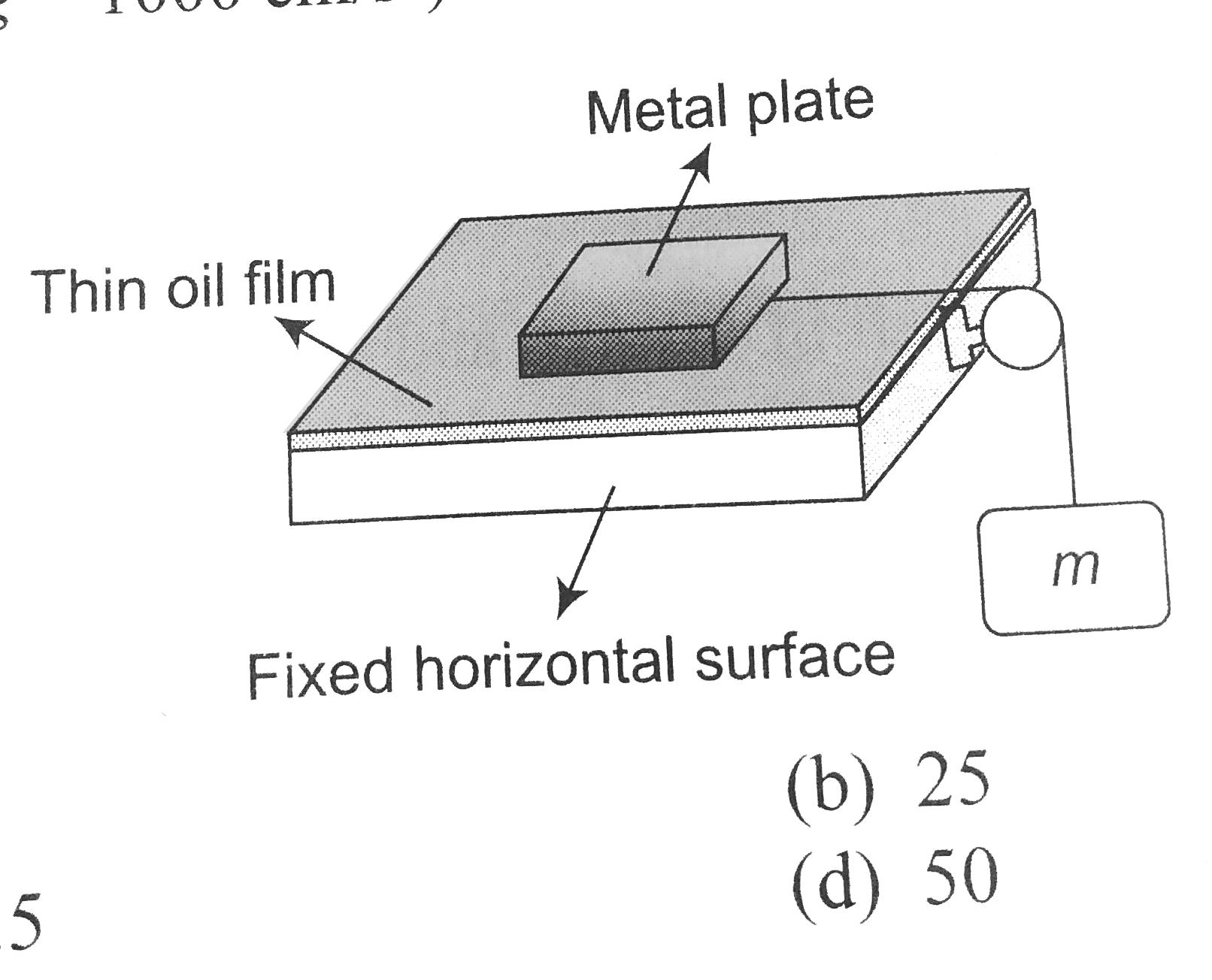
A rectangular metal plate has dimensions of `10cmxx20cm`. A thin film of oil separates the plate from a fixed horizontal surface. The separation between the rectangular plate and the horizontal surface is `0.2mm`. An ideal string is attached to the plate and passes over an ideal pulley to a mass `m`. When `m=125gm`, the metal plate moves at constant speed of `5(cm)/(s)`, across the horizontal surface. Then the coefficient of viscosity of oil in `(dyne-s)/(cm^2)` is (Use `g=1000(cm)/(s^2)`)
View Solution
A cubical block of side `a` and density `rho` slides over a fixed inclined plane with constant velocity `v`. There is a thin film of viscous fluid of thickness `t` between the plane and the block. Then the coefficient of viscosity of the thin film will be: (Acceleration due to gravity is g)
View SolutionWhen a ball is released from rest in a very long column of viscous. Liquid its downwards acceleration is `a` (just after release). Then its acceleration when it has acquired two third of the maximum velocity:
View SolutionA uniform solid sphere of relative density 5 is released in water filled in a long vertical tube. Its terminal velocity achived is `V`. If another uniform solid sphere of same material but double the radius is released in the same water then the terminal velocity achived will be.
View Solution
A container filled with viscous liquid is moving vertically downwards with constant speed `3v_0`. At the instant shown, a sphere of radius `r` is moving vertically downwards (in liquid) has speed `v_0`. The coefficient of viscosity is `eta`. There is no relative motion between the liquid and the container. Then at the shoen instant, The magnitude of viscous force acting on sphere is
View SolutionTwo uniform solid balls of same density and if radii `r` and `2r` are dropped in air and fall vertically downwards. The terminal velocity of the ball with radius `r` is `1cms^-1`, then the terminal velocity of the ball of radius `2r` will be (neglect buoyant force on the balls.)
View SolutionA sphere of radius R and density `rho_1` is dropped in a liquid of density `sigma`. Its terminal velocity is `v_1`. If another sphere of radius `R` and density `rho_2` is dropped in the same liquid, its terminal velocity will be:
View Solution
Viscosity questions and complete solutions for chapter PROPERTIES OF MATTER of A2Z PHYSICS (HINGLISH) of Class 11