Complete Solutions to Problems Based On Mixed Concepts of chapter PROPERTIES OF MATTER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | PROPERTIES OF MATTER |
| A2Z | Problems Based On Mixed Concepts |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |

The length of wire `OE` is divided into five equal parts `OA`, `AB`, `BC`, `CD` and `DE` The wire is hanging from `E` and its length is given by
`(5)/(4)(sigma)/(rhog)`, where `sigma` is the breaking stress and `rho` is the density of the material of the wire. Find the point at which wire will break
View SolutionA 40 kg boy whose leg are `4cm^2` in area and `50cm` long falls through a height of `2m` without breaking his leg bones. If the bones can stand a stress of `1.0xx10^8(N)/(m^2)`, calculate the Young's modulus for the material of the bone.
View SolutionA light rod of length `2 m` is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross section `0.1 cm^(2)`. The other wire is a brass of cross section `0.2 cm^(2)`. A weight is suspended from a certain point of the rod such that equal stress are produced in both the wires. Which of the following are correct?
View SolutionA uniform rod of length `l`, mass `m`, cross-sectional area `A` and Young's modulus `Y` is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity `omega`. Find the total extension in the rod due to the tension produced in the rod.
View SolutionIf the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are `a, b` and `c` respectively then the corresponding ratio of increase in their lengths is
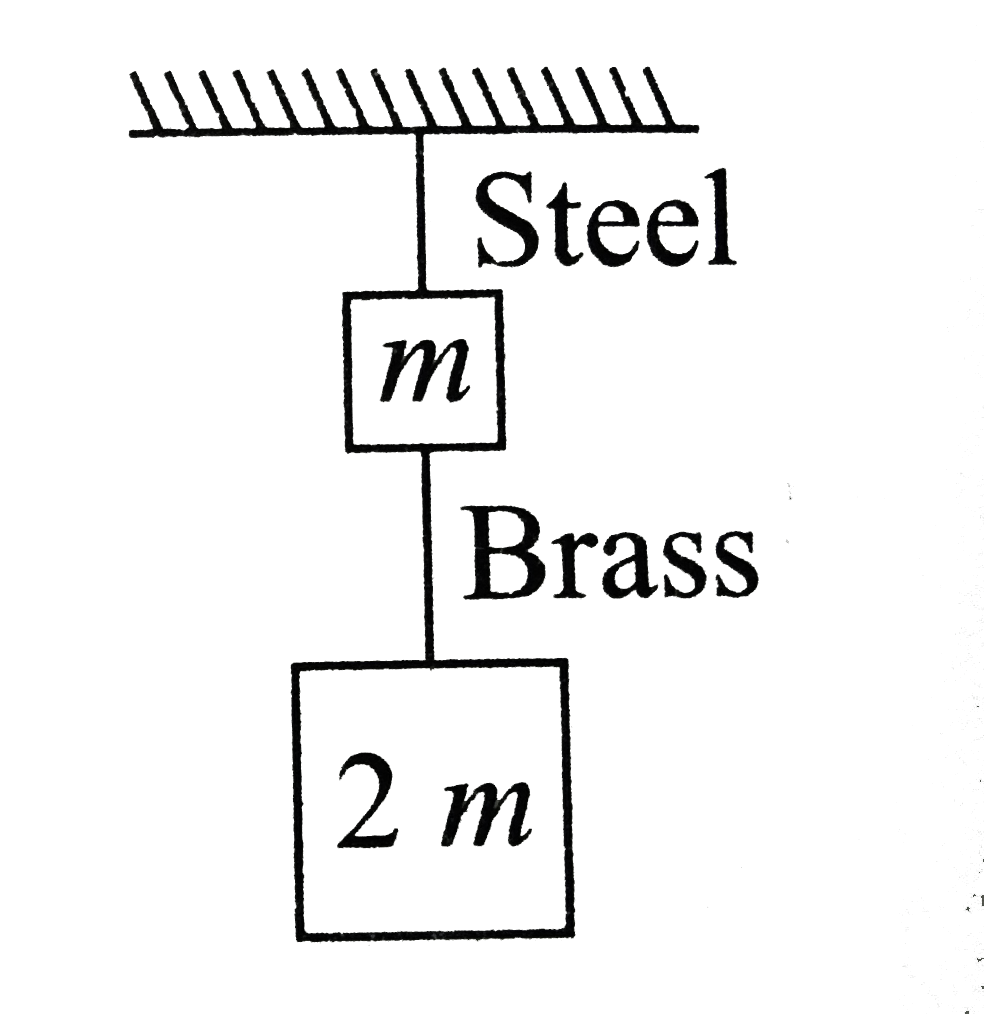
View Solution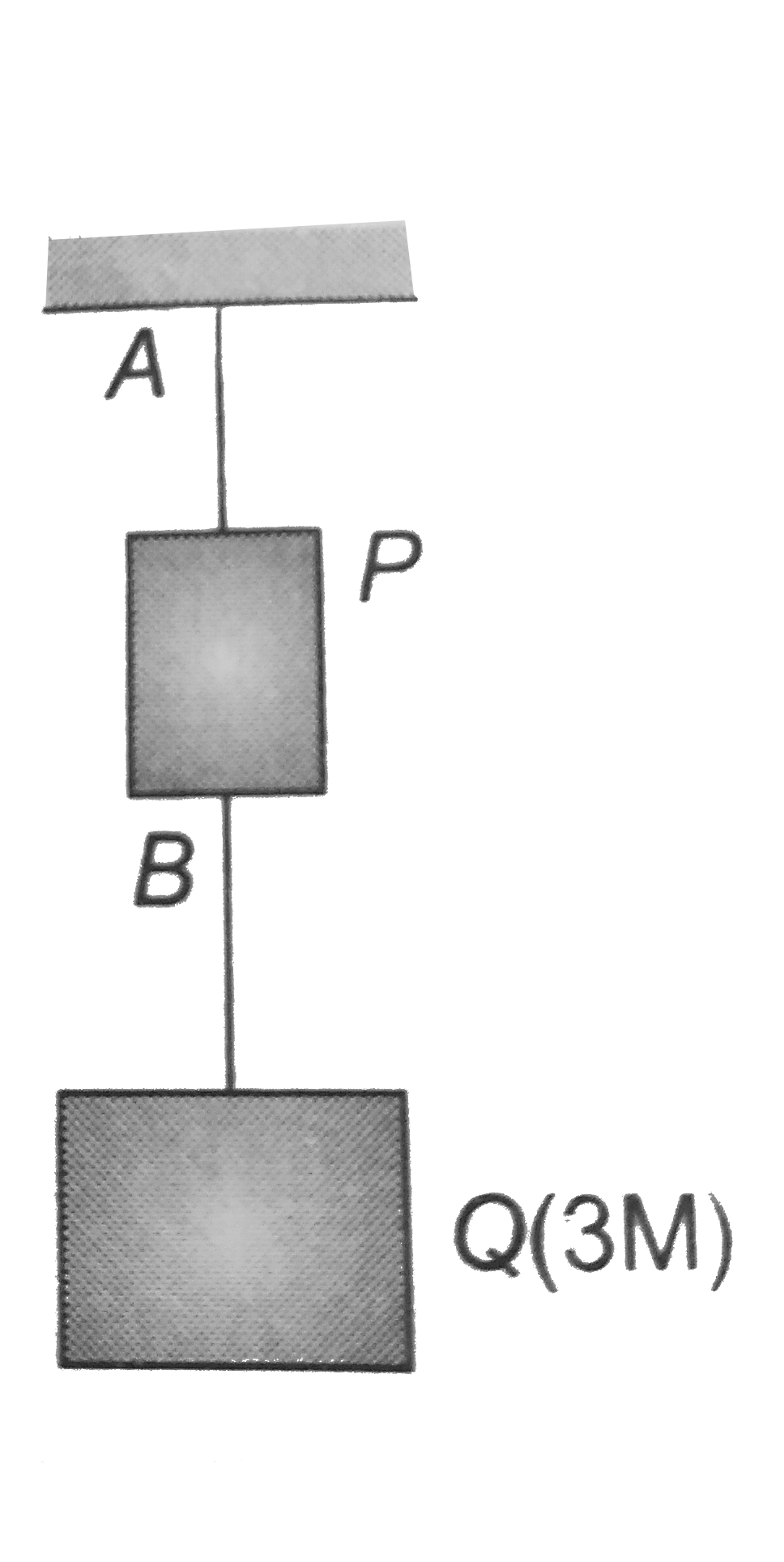
Wires A and B are connected with blocks P and Q, as shown, the ratio of lengths radii and Young's modulus of wires A and B are r, 2r and 3r respectively (r is a constant). Find the mass of block P if ratio of increase in their corresponding length is `(1)/(6r^2)`. The mass of the block Q is 3M
View Solution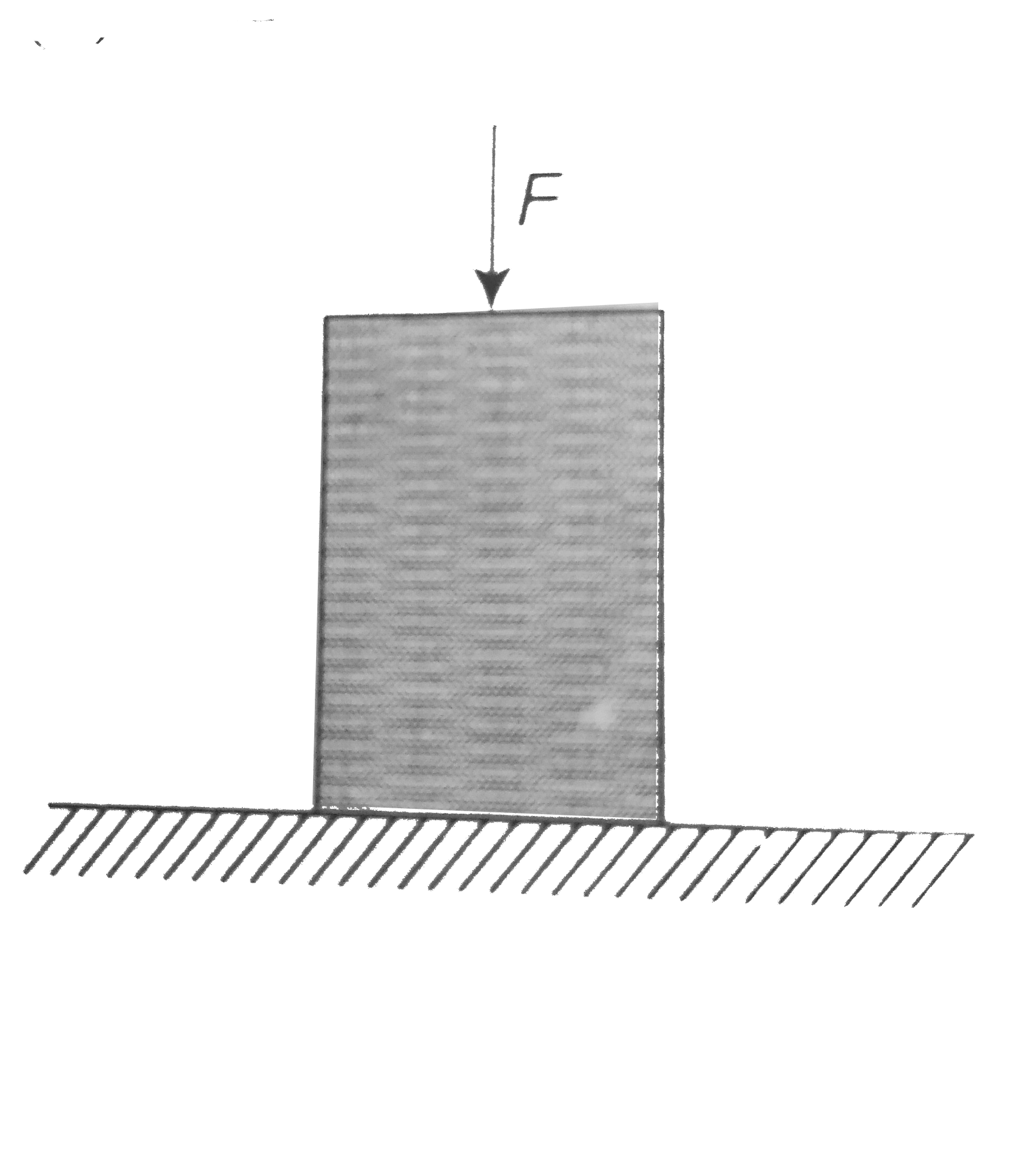
A metal cylinder of length `L` is subjected to a uniform compressive to a uniform compressive force `F` as shown in the figure. The material of the cylinder has Young's modulus `Y` and poisson's ratio `sigma` The change in volume of the cylinder is
View SolutionA uniform rod of length `l`, mass `m`, cross-sectional area `A` and Young's modulus `Y` is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity `omega`. Find the total extension in the rod due to the tension produced in the rod.
View SolutionA metal wire of length `L_1` and area of cross section A is ttached to a rigid support. Another metal wire of length `L_2` and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if `Y_1` and `Y_2` are the Young's moduli of the wires respectively the effective force constant of the system of two wires is
View SolutionA stone of mass `m` tied to one end of a wire of length L. the diameter of the wire is D and it is suspended vertically. The stone is now rotated in a horizontal plane and makes an angle 6 with the vertical. If Young's modulus of the wire is `Y`, Then the increase in the length of the wire is
View SolutionAssuming that shear stress at the base of a mountain is equal to the force per unit area due to its weight. Calculate the maximum possible height of a mountain on the earth if breaking stress of a typical rock is `3xx10^8Nm^-3` and its density `3xx10^-3kgm^-3`. (Take `g=10ms^-2`)
View SolutionTwo strips of metal are riveted together at their ends by four rivets, each of diameter 6 mm. Assume that each rivet is to carry one quarter of the load. If the shearing stress on the rivet is not to exceed `6.9xx10^7Pa`, the maximum tension that can be exerted by the riveted strip is
View SolutionTwo blocks of masses `1 kg` and `2 kg` are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is `(40//3pi)xx10^(6)N//m^(2)`. If `g=10ms^(-2)`, then what should be the minimum radius of the wire used if it is not to break?

View SolutionA uniform cylindrical wire is subjected to a longitudinal tensile stress of `5 xx 10^(7) N//m^(2)`. Young's modulus of the material of the wire is `2 xx 10^(11) N//m^(2)`. The volume change in the wire is `0.02%`. The fractional change in the radius is
View SolutionYoung's modulus of brass and steel are `10 xx 10^(10) N//m^(2)` and `2 xx 10^(11) N//m^(2)`, respectively. A brass wire and a steel wire of the same length are extended by `1 mm` under the same force. The radii of the brass and steel wires are `R_(B)` and `R_(S)` respectively. Then
View SolutionA material has normal density `rho` and bulk modulus `K`. The increase in the density of the material when it is subjected to an external pressure `P` from all sides is
View SolutionA rubber rope of length `8 m` is hung from the ceiling of a room. What is the increase in length of the rope due to its own weight? (Given: Young's modulus of elasticity of rubber `= 5 xx 10^(6) N//m^(2)` and density of rubber `=1.5xx10^(3)kg//m^(3)`. Take `g=10ms^(-2))`
View SolutionThe length of a metal wire is `l_1` when the tensionin it is `T_1 and is l_2` when the tension is `T_2`. The natural length of the wire is
View SolutionA wire is suspended vertically from a rigid support. When loaded with a weight in air, the wire extends by `16cm`. When the weight is completely immersed in Water, the extension is reduced to `14 cm`. The relative density of the material of the weight is
View SolutionIf the volume of a wire remains constant when subjected to tensile stress, the value of poisson's ratio of material of the wire is
View SolutionA material has Poisson ratio `0.5`. If a rod of material has a longitudinal strain `2xx10^-3`, the percentage change in volume is :
View SolutionA wire of cross section `A` is stretched horizontally between two clamps located `2l m` apart. A weight `W kg` is suspended from the mid-point of the wire. If the mid-point sags vertically through a distance `x lt l`, the strain produced is
View SolutionIn the above question the value of stress is:
View SolutionIf in the above question the Young's modulus of the material is Y, the value of extension x is:
View Solution
A container is partially filled with a liquid of density `rho_2` A capillary tube of radius r is vertically inserted in this liquid. Now another liquid of density `rho_1(rho_1ltrho_2)` is slowly poured in the container to a height h as shown. There is only denser liquid in the capillary tube. The rise of denser liquid in the capillary tube is also `h`. Assuming zero contact angle, the surface tension of heavier liquid is
View SolutionThe elongation in a metallic rod hinged at one end and rotating in a horizontal plane becomes four times of the intial value. The angular velocity of ratation becomes
View SolutionConsider the following statements:
(i) Young's modulus is numerically equal to the stress which will double the length of a wire.
(ii) Viscosity of gases is greater than that of liquids.
(iii) The surface tension of a liquid decreases due to the presence of insoluble contamination.
The number of above statements that are true is
View SolutionTwo soap bubbles of radii `a` and `b` coalesce to form a single bubble of radius `c`. If the external pressure is `P`, find the surface tension of the soap solution.
View SolutionCalculate the pressure inside a small air bubble of radus `r` situated at a depth `h` below the free surface of liquids of densities `rho_(1)` and `rho_(2)` and surface tennsions `T_(1)` and `T_(2)`. The thickness of the first and second liquids are `h_(1)` and `h_(2)` respectively. Take atmosphere pressure `=P_(0)`.

View SolutionA glass plate of length `10 cm`, breadth `1.54 cm` and thickness `0.20 cm` weigh `8.2 g` in air. It is held vertically with the long side horizontal and the lower half under water. Find the apparent weight of the plate. Surface tension of water `=7.3xx10^(-2)N//m` and `=9.8ms^(-12)`
View SolutionA rubber cord has a cross -sectional area `1 mm^(2)`and total unstretched length`10.0cm`. It is streched to `12.0 cm` and then released to project a missile of mass 5.0 g.Taking young's modulus Y for rubber as `5.0xx10^(8) N//m^(2)`.Calculate the velocity of projection .
View Solution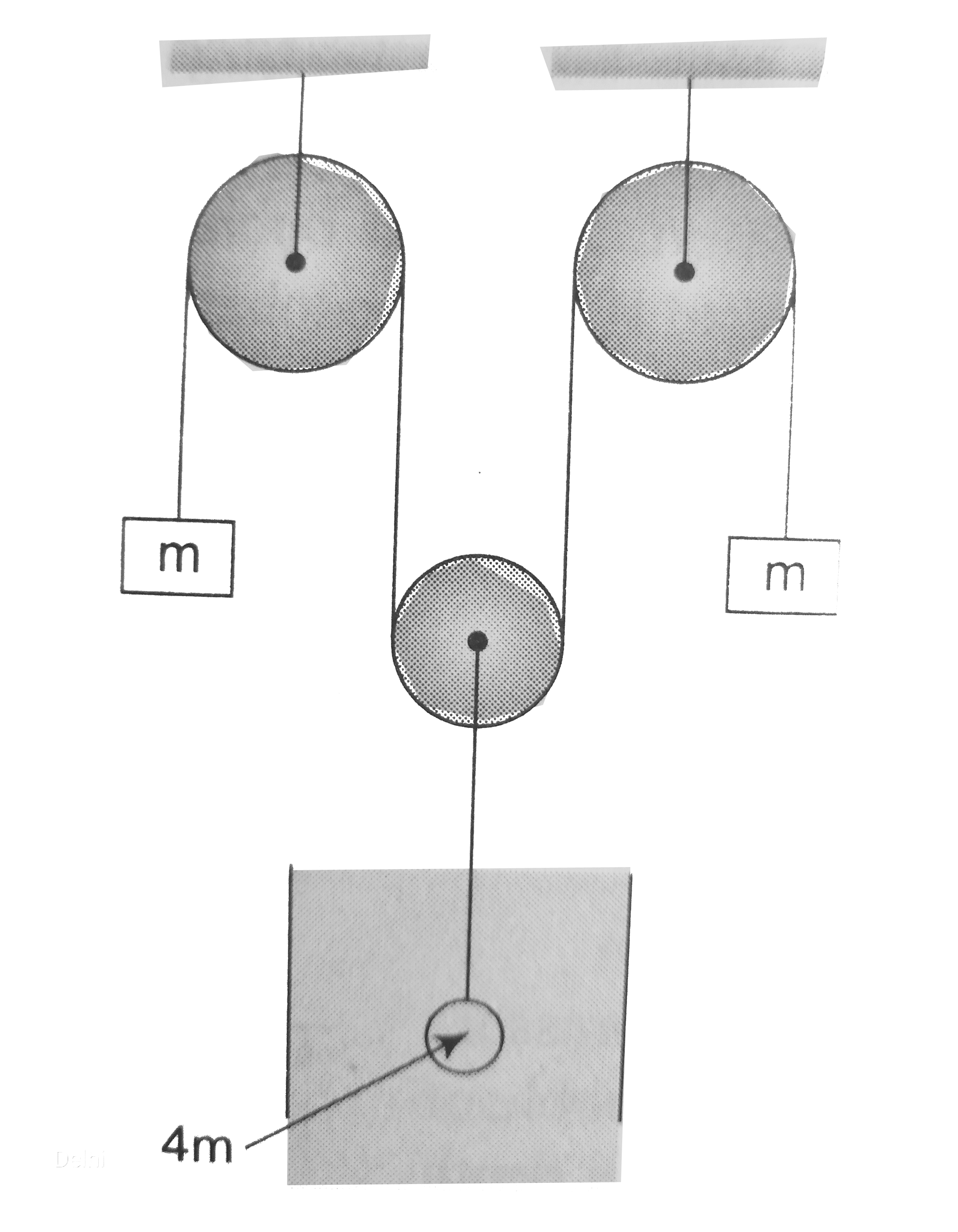
A spherical ball of mass 4m, density `sigma` and radius `r` is attached to a pulley-mass system as shown in figure. The ball is released in a liquid of coefficient of viscosity `eta` and density `rho(lt(sigma)/(2))`. If the length of the liquid column is sufficiently long, the terminal velocity attained by the ball is given by (assume all pulleys to be massless and string as massless and inextensible):
View SolutionA man is rowing a boat with a constant velocity `v_(0)` in a river. The contact area of boat is `'A'` and coefficient of viscosity is `eta`. The depth of river is `'D'` . Find the force required to row the boat.
View SolutionA metal ball `B_(1)` (density `3.2g//"cc")` is dropped in water, while another metal ball `B_(2)` (density `6.0g//"cc")` is dropped in a liquid of density `1.6g//"cc"`. If both the balls have the same diameter and attain the same terminal velocity, the ratio of viscosity of water to that of the liquid is
View Solution
Problems Based On Mixed Concepts questions and complete solutions for chapter PROPERTIES OF MATTER of A2Z PHYSICS (HINGLISH) of Class 11