Complete Solutions to Surface Tension And Surface Energy of chapter PROPERTIES OF MATTER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | PROPERTIES OF MATTER |
| A2Z | Surface Tension And Surface Energy |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
The rain are in spherical shape due to
View SolutionSoap helps in cleaning clothes, because
View SolutionThe spider and insect move and run about on the surface of water without sinking because
View Solution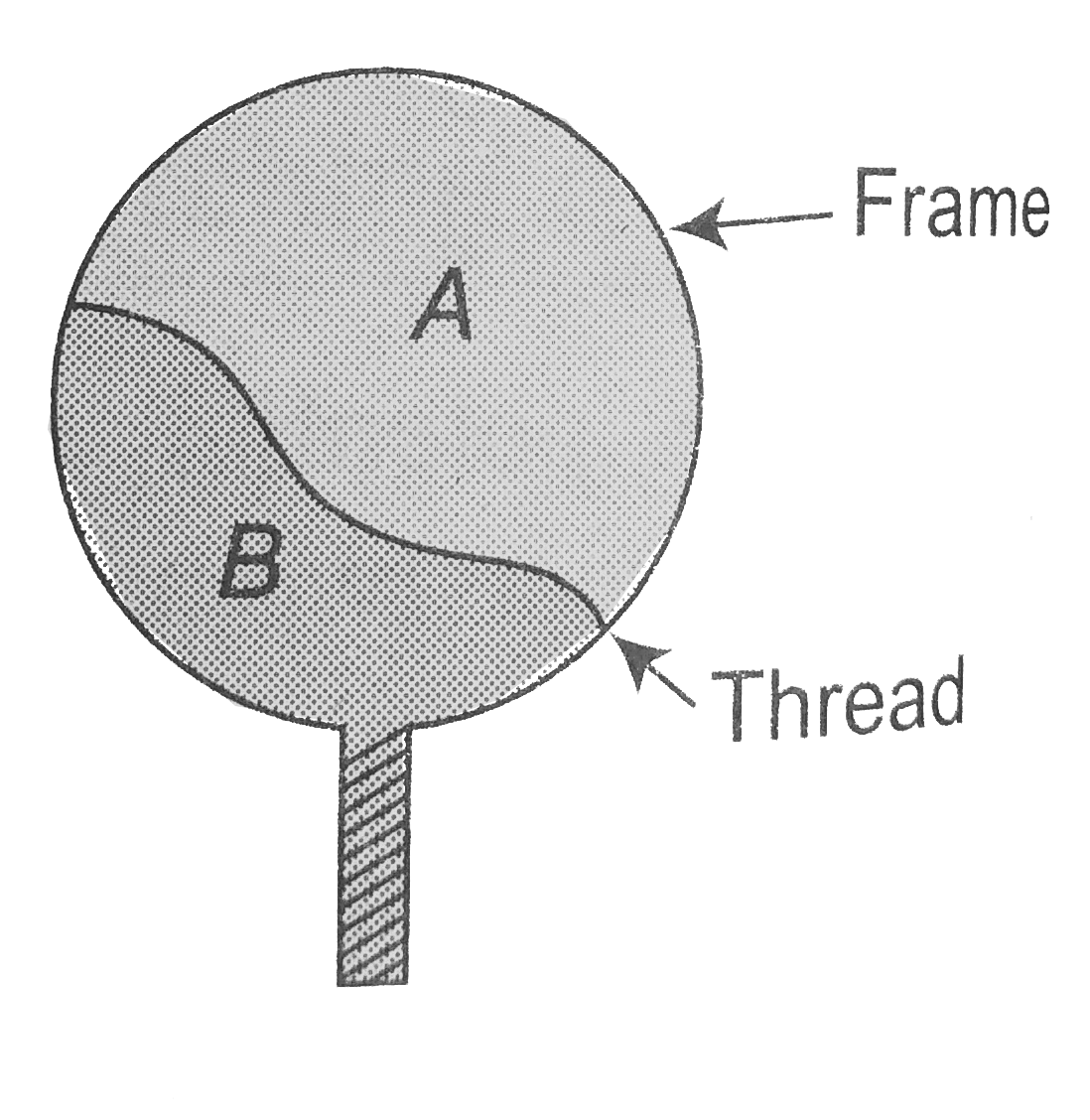
A thread is tied slightly loose to a wire frame as in figure and the frame is dipped into a soap solution and taken out . The frame is comletely covered with the film. When the portion `A` puntured with a pin The thread.
View SolutionThe maximum force, in addition to the weight required to pull a wire of `5.0cm` long from the surface of water at temperature `20^@C`, is 728 dynes. The surface tension of water is
View SolutionConsider a liquid contained in a vessel. The liquid solid adhesive force is very weak as compared to the cohesive force in the liquid. The shape of the liquid surface near the solid shall be
View SolutionA thin metal disc of radius `r` floats on water surface and bends the surface downwards along the perimeter making an angle `theta` with vertical edge of the disc of the disc. If the disc dispplaces a weight of water `W` and surface tension of water is `T`, then the weight of metal disc is
View SolutionA thin liquid film formed between a U-shaped wire and a light slider supports a weight of `1.5xx10^-2N` (see figure). The length of the slider is 30cm and its weight negligible. The surface tension of the liquid film is

View SolutionEnergy needed in breaking a drop of radius `R` into `n` drops of radii `r` is given by
View SolutionThe radius of a soap bubble is increased from `(1)/(sqrtpi)` cm to `(2)/(sqrtpi)` cm. If the surface tension of water is `30dynes` per cm, then the work done will be
View SolutionOne thousand small water drops of equal radii combine to form a big drop. The ratio of final surface energy to the total initial surface energy is
View SolutionA film of water is formed between two straight parallel wires of length 10 cm each separated by `0.5cm` If their separation is increased by `1mm` while still maintaining their parallelism, how much work will have to be done (Surface tension of water `=7.2xx10^-2(N)/(m)`)
View SolutionThere is a howizontal film of soap solution. On it a thread is placed in the form of a loop. The film is pierced inside the loop and the thread becomes a circular loop of radius `R`. If the surface tension of the loop be `T`, then what will be the tension in the thread?
View SolutionIf a number of little droplets of water, each of radius `r`, coalesce to form a single drop of radius `R`, show that the rise in temperature will be given by `(3T)/J(1/r-1/R)` where `T` is the surface tension of water and `J` is the mechanical equivalent of heat.
View Solution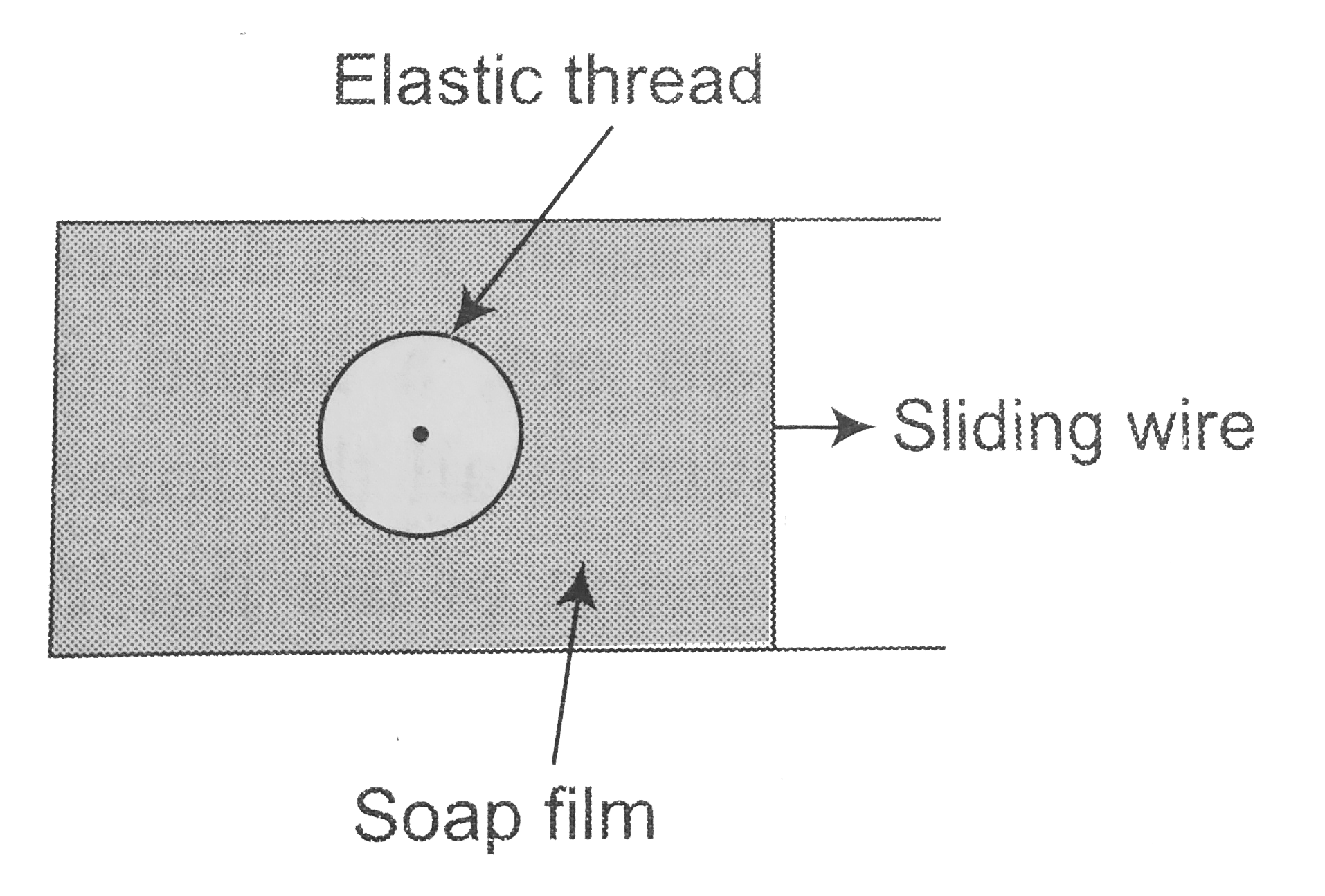
The figure shows a soap film in which a closed elastic thread is lying. The film inside the thread is pricked. Now the sliding wire is moved out so that the surface area increases. The radius circle of the circle formed by elastic thread will
View Solution
A long capillary tube of mass `pi` gm, radisu `2mm` and negligible thickness, is partially immersed in a liquid of surface tension `0.1(N)/(m)`. Take angle of contact zero and neglect buoyant force of liquid. The force required to hold the tube vertically, will be `(g=10(m)/(s^2)`)
View Solution
The surface tension of water is `75(dyne)/(cm)`. Find the minimum vertical force required to pull a thin wire ring up (refer figure) if it is initially resting on a horizontal water surface. The circumference of the ring is `20cm` and its weight is `0.1N`
View SolutionA paper disc of radius `R` from which a hole of radius `r` is cut out is floating in a liquid of the surface tension `S`. The force on the disc due to the surface tension is
View SolutionA wire of mass `1g` is kept horizontally on the surface of water. The length of the wire that does not break the surface film is (surface tension of water is `70dynecm^-1`)
View SolutionA liquid is containe in a vertical tube of semicircular cross section figure.The contact angle is zero. The force of surface tension on the curved part and on the flat part are in ratio

View SolutionA wire ring of diameter `14cm` is gently lowered on to a liquid surface and then pulled up. When the film just breaks, the force required is `0.0616N`. The surface tension of the liquid is
View SolutionA square wire frame of length `l` is dipped in a solution. When the frame is taken out, a liquid film is formed. What is the algebraic sum of all the force acting on the frame due to surface tension of the liquid? (given`sigma=`surface tension of the liquid).
View SolutionA soap film measure `10cmxx6cm`. It is increased to `10cmxx12cm`. IF surface tension is `30xx10^-3` newtor per metre. Then the work done is
View SolutionIf work `W` is done in blowing a bubble of radius `R` from a soap solution. Then the work done is blowing a bubble of radius `2R` from the same solution is
View SolutionThe surface tension of a liquid is `5Nm^-1`. If a thin film formed on a loop of area `0.02m^-2` then its surface energy will be
View SolutionA soap bubble has radius `r` The work done in increasing its radius to three times its original radius, without any rise of temperature, is (Given Surface tension of soap solution is `T`)
View SolutionA mercury drop of radius `R` is sprayed into `n` droplets of equal size. Calculate the energy expended if surface tension of mercury is `T`.
View SolutionAn annular disc of radius `r_(1 )= 10 cm` and `r_(2) = 5 cm` is placed on a water surface. Find the surface tension force on the disc if we want to pull it from water surface. Take coefficient of surface tension as `sigma= 7 xx10^(-3) N//m, g = 10 ms^(-2)`.

View SolutionA film of water is formed between two straight parallel wires of length 10 cm each separated by `0.5cm` If their separation is increased by `1mm` while still maintaining their parallelism, how much work will have to be done (Surface tension of water `=7.2xx10^-2(N)/(m)`)
View Solution
Surface Tension And Surface Energy questions and complete solutions for chapter PROPERTIES OF MATTER of A2Z PHYSICS (HINGLISH) of Class 11