Complete Solutions to Transmission Of Heat : Conduction of chapter THERMAL PROPERTIES OF MATTER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | THERMAL PROPERTIES OF MATTER |
| A2Z | Transmission Of Heat : Conduction |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
Two bars of thermal conductivities `K` and `3K` and lengths `1 cm` and `2 cm` respectively have equal cross-sectional area, they are joined lengths wise as shown in the figure. If the temperature at the ends of this composite bar is `0^(@)C` and `K^(2)//l` respectively (see figure), then the temperature `phi` of the interface is
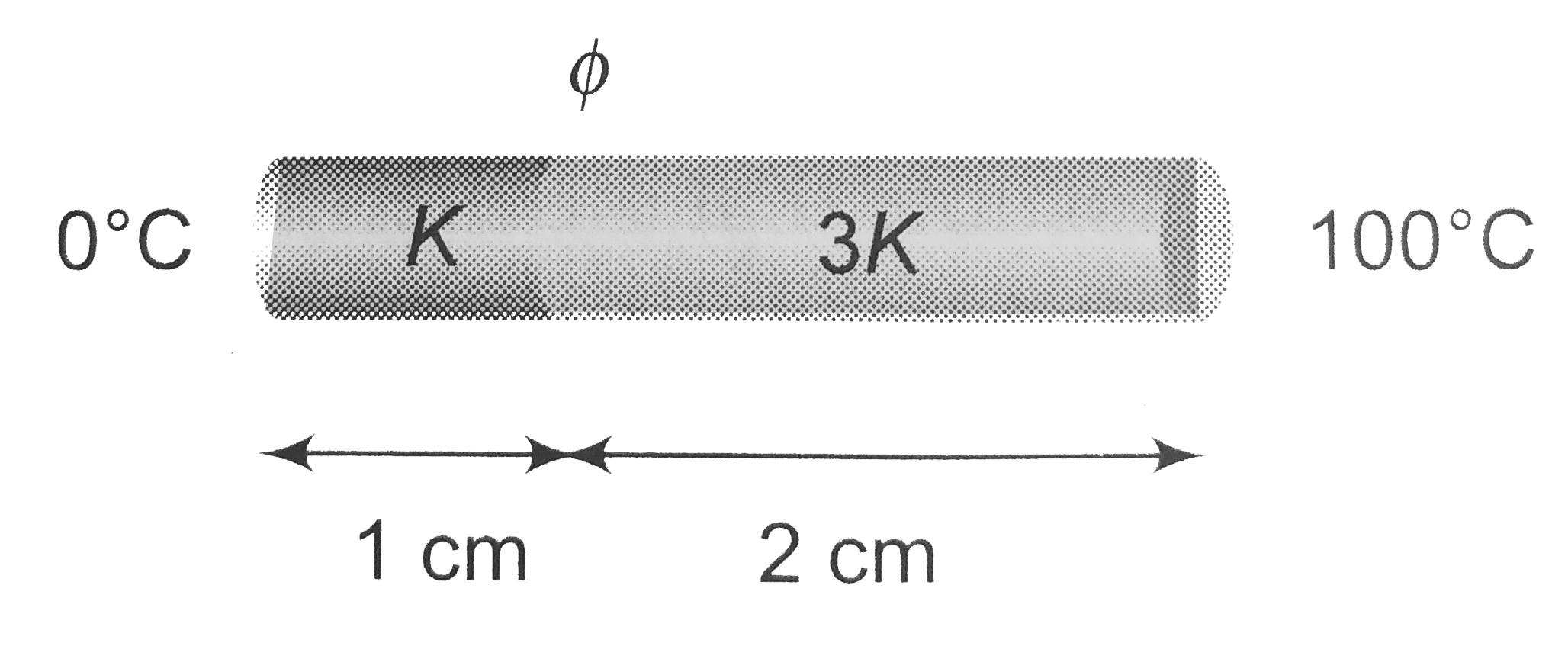
View SolutionA compound slab is made of two parallel plates of copper and brass of the same thickness and having thermal conductivities in the ratio `4:1`. The free face of copper is at `0^(@)C`. The temperature of the internal is `20^(@)C`. What is the temperature of the free face of brass?
View SolutionTwo identical vessels are filled with equal amounts of ice. The vessels are made from different materials. If the ice melts in the two vessels in times `t_(1) and t_(2)` respectively, then their thermal conductivities are in the ratio
View SolutionThe heat is flowing through two cylinderical rods of same material. The diameters of the rods are in the ratio `1:2` and their lengths are in the ratio `2:1`. If the temperature difference between their ends is the same, the ratio of rates of flow of heat through them will be
View SolutionThe temperature gradient in a rod of `0.5 m` length is `80^(@)C//m`. It the temperature of hotter end of the rod is `30^(@)C`, then the temperature of the cooler end is
View SolutionIf the coefficient of conductivity of aluminium is `0.5 cal cm^(-1) s^(-1).^(@)C^(-1)`, then the other to conductor `10 cal s^(-1) cm^(-2)` in the steady state, the temperature gradient in aluminium must be
View SolutionThe coefficient of thermal conductivity of copper, mercury and glass are respectively `K_(c), K_(m)` and `K_(g)` that `K_(c) gt K_(m) gt K_(g)`. If the same quantity of heat is to flow per second per unit of each and corresponding temperature gradients are `X_(c), X_(m)` and `X_(g)`, then
View SolutionIce has formed on a shallow pond, and a steady state has been reached, with the air above the ice at `-5.0^(@)C` and the bottom of the pond at `40^(@)C`. If the total depth of ice + water is `1.4 m`, (Assume that the thermal conductivities of ice and water are `0.40` and `0.12 cal//m C^(@)s`, respectively.)
The thickness of ice layer is
View SolutionIf l is the length, A is the area of cross-section and K the thermal conductivity, then the thermal resistance of the block is given by
View SolutionA wall has two layers A and B each made of different materials. The layer A is 10cm thick and B is 20 cm thick. The thermal conductivity of A is thrice that of B. Under thermal equilibrium temperature difference across the wall is `35^@C`. The difference of temperature across the layer A is
View SolutionTwo rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.

View SolutionTwo spheres of different materials one with double the radius and one-fourth wall thickness of the other are filled with ice. If the time taken for complete melting of ice in the larger sphere is `25` minutes and for smaller one is `16` minutes, the ratio of thermal conductivities of the materials of larger sphere to that of smaller sphere is:
View SolutionA wall has two layers A and B each made of different materials. The thickness of both the layers is the same. The thermal conductivity of A, `K_(A) = 3K_(B)`. The temperature different across the wall is `20^(@)C` in thermal equilibrium
View SolutionA cylinder of radius `R` made of a material of thermal conductivity `K_1` is surrounded by a cylindrical shell of inner radius `R` and outer radius `2R` made of a material of thermal conductivity `K_2`. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effective thermal conductivity of the system is
View SolutionTwo ends of a conducting rod of varying cross-section are maintained at `200^(@)C` and `0^(@)C` respectively. In steady state:

View SolutionOne end of conducting rod is maintained at temperature `50^(@)C` and at the other end ice is melting at `0^(@)C`. The rate of melting of ice is doubled if:
View SolutionA wall has two layers A and B each made of different materials. Both the layers have the same thickness. The thermal conductivity of materials A is twice of B. Under thermal equilibrium temperature difference across the layer B is `36^@C`. The temperature difference across layer A is
View SolutionThree rods made of the same material and having the same cross-section have been joined as shown in the figure. Each rod is of the same length. The left and right ends are kept at `0^@C` and `90^@C`, respectively. The temperature of junction of the three rods will be

View SolutionAll the rods have same conductance `'K'` and same area of cross section '`A'`. If ends A and C are maintained at temperature `2T_(0)` and `T_(0)` respectively then which of the following is`//`are correct?
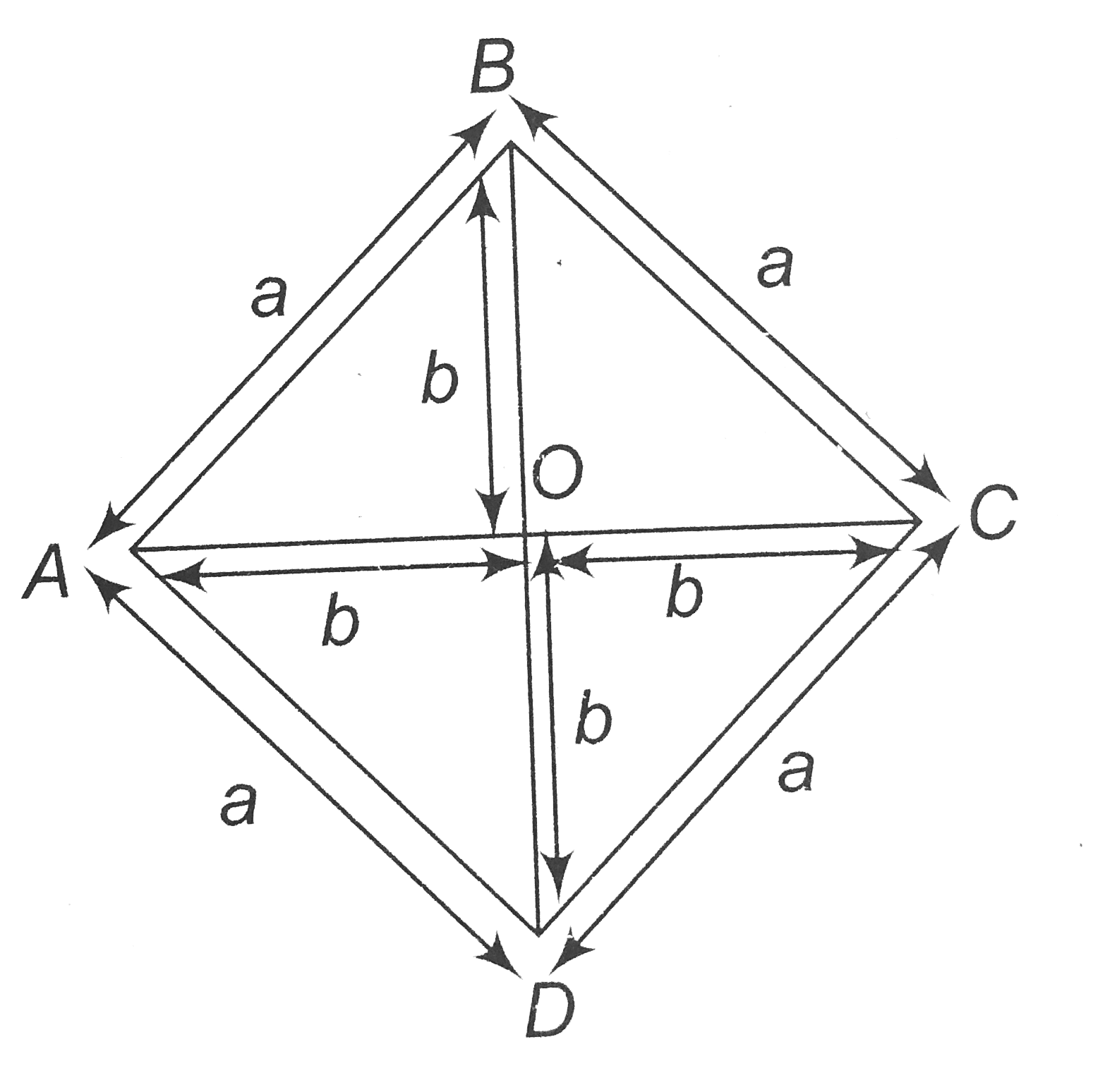
View SolutionTwo identical long, solid cylinders are used to conduct heat from temp `T_(1)` to Temp `T_(2)`. Originally the cylinders are connected in series and the rate of heat transfer is H. If the cylinders are connected in parallel then the rate of heat transfer would be:
View SolutionTwo identical rectangular rods of metal are welded end to end in series between temperature `0^(@)C` and `100^(@)C and 10 J` of heat is conducted (in steady state process) through the rod in `2.00 min.` if `5` such rods are taken and joined as shown in figure maintaining the same temperature difference between A and B, then the time in which `20 J` heat will flow through the rods is
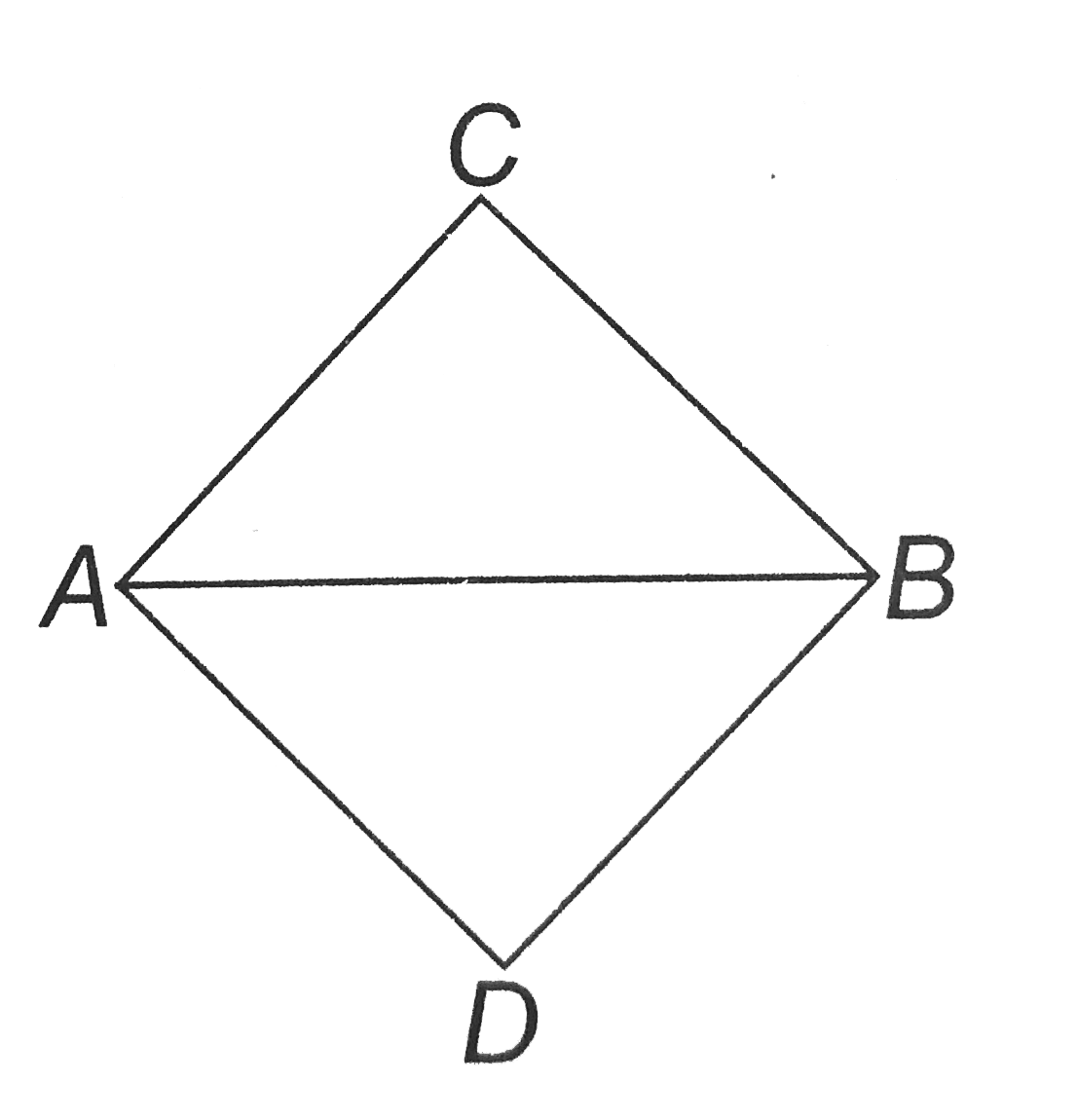
View SolutionFigure shows in cross section a wall consisting of four layers with thermal conductivities `K_(1) = 0.06 W // mK, K_(3) = 0.04 W// mK and K_(4) = 0.10 W// mK`. The layer thickness are `L_(1) = 1.5 cm, L_(3) = 2.8 cm and L_(4) = 3.5 cm`. The temperature of interfaces is as shown in figure. energy transfer through the wall is in steady state. the temperature of the interface between layer `3 and 4` is:

View SolutionThe temperature of the interface between layer `2 and 3` is:
View SolutionIf layer thickness `L_(2)` is `1.4 cm`, then its thermal conductivity `K_(2)` will have value `("in " W//mK)`
View SolutionA cylinder A of a material of thermal conductivity `K_(1)` is surrounded by a cylindrical shell of inner radius equal to the cylinder. The shell is made of a material of thermal conductivity `K_(2)`. The two ends of the combined system are maintained at two different temperature. if the effective thermal conductivity of the system is `(4K_(1) + 5K_(2))/(9)`, find the rate of outer radius of the shell to the radius of the cylinder.

View SolutionIce starts forming in lake with water at `0^(@)C` and when the atmospheric temperature is `-10^(@)C`. If the time taken for `1 cm` of ice be `7` hours. Find the time taken for the thickness of ice to change from `1 cm` to `2 cm`
View SolutionA slab `X` of thickness `'t'`, thermal conductivity `'K'` and area of cross-section `'A'` is placed in thermal contact with another slab `Y` which is `2n^(2)` times thicker, `4n` times conductive and having `n` times larger cross-section area. If the outside face of `X` is maintained at `100^(@)C`, the outside face of `Y` at `0^(@)C`, then the temperature of the junction is represented by the graph `(ngt0)`
View SolutionThe graph shown gives the temperature along an `X` axis that extends directly through a wall consisting of three layers `A`, `B` and `C`. The air temperature on one side of the wall is `150^(@)C` and on the other side is `80^(@)C`. Thermal conduction through the wall is steady. Out of the three layers `A` `B` and `C`, thermal conductivity is greatest of the layer
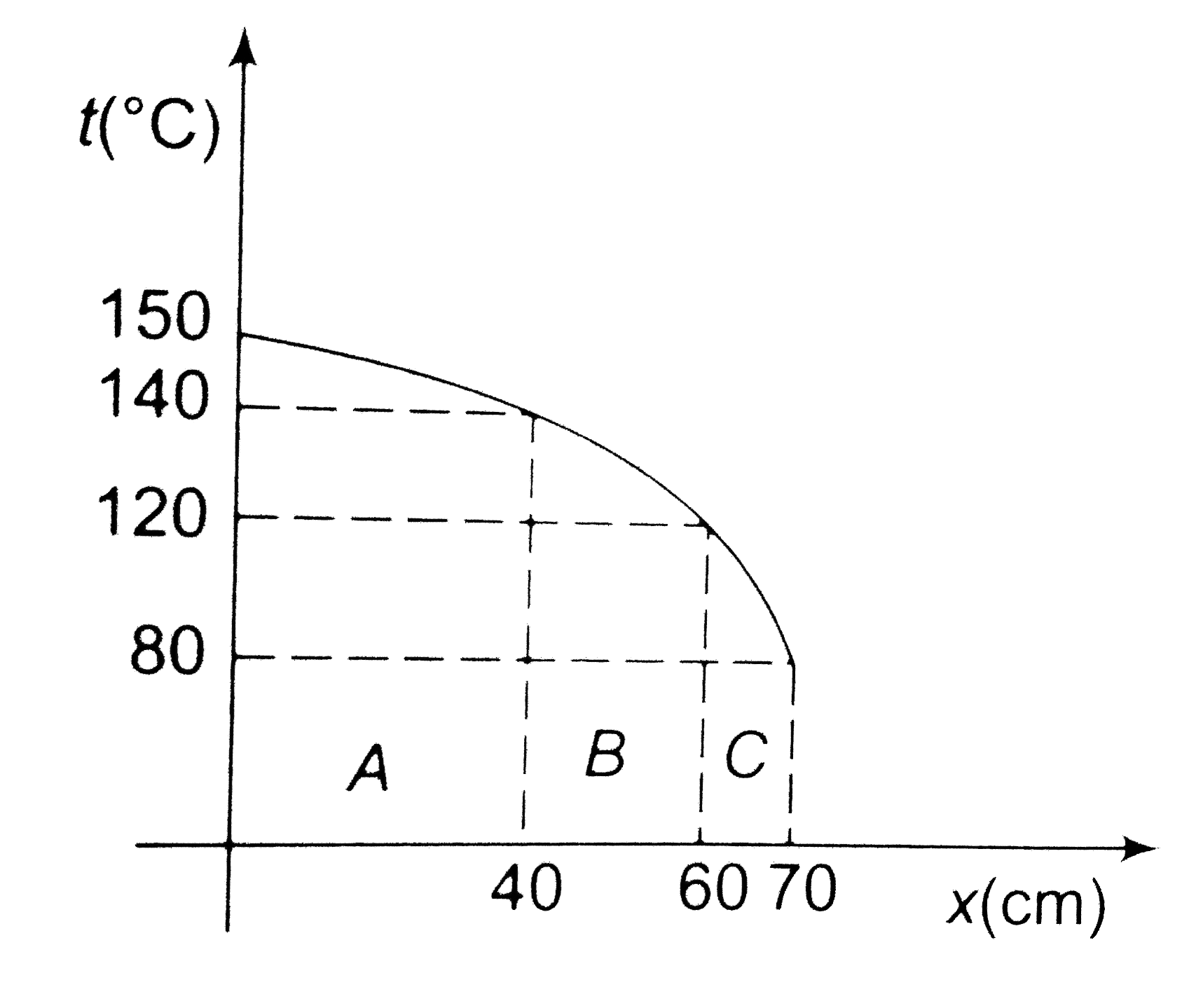
View Solution
Transmission Of Heat : Conduction questions and complete solutions for chapter THERMAL PROPERTIES OF MATTER of A2Z PHYSICS (HINGLISH) of Class 11