Complete Solutions to Solved Example of chapter ATOMIC STRUCTURE of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | ATOMIC STRUCTURE |
| ALLEN | Solved Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
If no. of protons in `X^(-2)` is `16`. Then no. of `e^(-)` in `X^(+2)` will be-
View SolutionIn `C^(12)` atom if mass of `e^(-)` is doubled and mass of proton is halved, then calculate the percentage change in mass no. of `C^(12)`
View SolutionAssuming that atomic weight of `C^(12)` is `150` unit from atmic table, then according to this assumption, the weight of `O^(16)` will be:-
View SolutionAn `alpha`-particle having `K.E. =7.7MeV` is scattered by gold `(z=79)` nucleus through `180^(@)` Find distance of closet approach.
View Solution`A` particular radiostation broadcasts at a frequency of `1120` Kilo Hertz another radio station broadcasts at a frequency of `98.7` mega Hertz. What are the wave length of radiations from each station?
View SolutionHow long would it take a radio wave of frequency `6xx10^(3) sec^(-1)` to travel from mars to the earth, a distance of `8xx10^(7)km` ?
View SolutionAt the closest approach, the distance between Mars and Earth is found to be `58` million `km`. When planets are at this closest distance, how long would it take to send a radio message from a space probe of mars to earth?
View Solution`A` sodium street light gives off yellow light that has a wavelength of `589nm`. What is the frequency of this light?
View Solutionthe vividh bharati station of All india Radio, Delhi , broadcasts on a frequency of 1,368 kHz (kilo hertz). Calculate the wavelength of the electromagnetic radiation emitted by transmitter . Which part of the electromagnetic spectrum does it belong to
View Solution`A` near ultra violet photon of wavelength `300nm` is absorbed by a gas and then emitted as two photons. One photons is of red light with wavelength `760nm`. What would be the wave length of the second photon?
View SolutionCalculate the frequency `&` energy of a photon of wave length `4000A`.
View SolutionHow many photons of lights having a wave length of `5000 A` are necessary to provide `1` Joule of energy?
View Solution`A` photon of wavelenth `3000` A strikes `a` metal surface, the work function of the metal being `2.20eV`. Calculate `(i)` the energy of the photon in `eV(ii)` the kinetic energy of the emitted photo electron and `(iii)` the velocity of the photo electron.
View SolutionPhotoelectrons are liberated by ultra light of wavelength `2000 Å` from a metallic surface for which the photoelectric threshold is 4000Å. Calculate the de Broglie wavelenth of electrons emitted with maximum kinetic energy.
View SolutionWhat does the negative electronic energy (negative sign for all values of energy) for hydrogen atom means?
View SolutionCalculate the radius of `1^(st), 2^(nd),3^(rd),4^(th)` Bohr's Orbit of hydrogen.
View SolutionCalculate the radius ratio of `3^(rd) & 5^(th)` orbit of `He^(+)`.
`r=0.529xx(n^(2))/(Z) Å`
At. Number of of He `=2`
View SolutionCalculate the radius ratio of `2^(nd)` orbit of hydrogen and `3^(rd)` orbit of `Li^(+2)`
View SolutionThe ratio of the radius of two Bohr's orbit of `Li^(+2)` is `1:9`. What would be their nomenclature.
View SolutionCalculate the radius of `2^(nd)` excited state of `Li^(+2)`
View SolutionCalculate the radius ratio of `2^(nd)` excited state of `H & 1^(st)` excited state of `Li^(+2)`.
View SolutionCalculate the energy of `Li^(+2)` atom for `2^(nd)` excited state.
View SolutionCalculate the ratio of energies of `He^(+)` for `1^(st) & 2^(nd)` excited state.
View SolutionIf the `P.E.` of an electron is `-68 eV` in hydrogen atom then find out `K.E.,E` of orbit where electron exist `&` radius of orbit.
View SolutionThe ionization energy for the hydrogen atom is `13.6 eV` then calculate the required energy in `eV` to excite it from the ground state to `1^(st)` excited state.
View SolutionIf the total energy of an electron is `-1.51 eV` in hydrogen atom then find out `K.E,P.E.`, orbit radius and velocity of the electron in that orbit.
View SolutionCalculate the velocity of an electron placed in the `3^(rd)` orbit of the `Li^(2+)` ion. Also calculate the number of revolution per second that it makes around the nucleous.
View SolutionIn a hydrogen spectum if electron moves from `7` to `1` orbit by transition in multi steps then find out the total number of lines in the spectum.
View SolutionIn a hydrogen spectum if electron moves from `6^(th)` to `2^(nd)` by transition in multi steps then find out the number of lines in spectum
View SolutionIn a hydrogen spectum if electron moves from `6^(th)` to `2^(nd)` by transition in multi steps then find out the number of lines in spectum
View SolutionIn Balmer series of `H` atom spectrum, which electronic transitions represents `3^(rd)` line?
View SolutionWhat is the wavelength of light emitted when the electron in a hydrogen atom undergoes transition from the energy level with `n=4` to the energy level with `n=1` ?
View SolutionCalculate the wavelength of the first and the last line in the Balmer series of hydrogen spectrum?
View SolutionCalculate the de Broglie wavelength of a ball of mass `0.1 kg` moving with a speed of `30 ms^(-1)`
View SolutionThe mass of a particle is `1mg` and its velocity is `4.5xx10^(5)cm` per second. What should be the wavelength of this particle if `h=6.652xx10^(-27) "erg second"`.
View SolutionWhich of the following should be the wavelength of an electron if its mass is `9.1xx10^(-31)kg` and its velocity is `1//10` of that of light and the value of `h` is `6.6252xx10^(-24)` joule second?
View SolutionWhat should be the momentum (in gram cm per second) of a particle if its De Broglie wavelength is `1Å` and the value of `h` is `6.6252xx10^(-27)` erg second?
View SolutionWhat should be the mass of the sodium photon if its wavelength is `5894Å`, the velocity of light is `3xx10^(8)` metre//second and the value of `h` is `6.6252xx10^(-34)kg m^(2)//sec`. ?
View SolutionCalculate de-Broglie wavelength when `e^(-)` is accelerated by the following voltage.
(i) `750V` (ii) `300` volt
View SolutionFind de-Broglie wavelength of electron with `KE =9.6xx10^(-19)J`.
View SolutionWhat is a particle or matter wave and how it is different from electro-megnetic wave?
View SolutionWhy electron cannot exist inside the nucleous according to heisnberg's uncertainty principle ?
View SolutionThe uncertainty in the momentum of a particle is `6xx10^(-9)kg ms^(-1)`. Calculate the uncertainty in its position.
View SolutionA golf ball has a mass of 40 g , and a speed of 45m/s. if the speed can be measured with in accuracy of 2 % . Calculate the uncertainty in the position .
View SolutionCalculate the uncertainty in velocity of a cricket ball (mass = 0.15 kg) if its uncertainty in position is of the order of `1Å`
View SolutionCompare Schrodinger equation with most important equation of Newtions law.
`(del^(2)psi)/(delx^(2))+(del^(2)psi)/(dely^(2))+(del^(2)psi)/(delz^(2))=-(E-V)(8pi^(2)m)/(h)psi " ""Schrodinger equation" ....(i)`
`m(d^(2)x)/(dt^(2))=Fm " ""Newton's law"" "....(ii)`
View SolutionFind the distance at which probability of finding electron is maximum for `1s` orbital in a He atom. The wave function orbital given as.
`psi_(1s)=(4)/(a_(0)^(3//2))e^((2r)/(a_(0))`
View SolutionConsider `psi` (wave function) of `2s` atomic orbital of H-atom is-
`psi_(2s)=(1)/(4sqrt(2pia_(0)^(3//2)))[2-(r )/(a_(0))]e^.(r )/(2a_(0)`
Find distance of radial node from nucleous in terms of `a_(0)`
View SolutionFor an orbital in `B^(+4)` radial function is :
`R(r ) = (1)/(9sqrt(6))((z)/(a_(0)))^((3)/(4))(4-sigma)sigma e^(-sigma//2`
where `sigma = (Zr)/(a_(0))` and `a_(0)=0.529Å,Z` = atomic number, `r=` radial distance from nucleus.
The radial node of orbital is at distance from nucleous.
View SolutionFor 2s orbital , `Psi_(r) = (1)/(sqrt(8))((z)/(a_(0)))^((3)/(2))(2-(zr)/(a_(0)))e^((zr)/(2a_(0)))` then , hydrogen radial node will be at the distant of
View Solution`psi_(1s)=(1)/(sqrt(pia_(0)^(3//2)))e^((r )/(a_(0)))`
Find the distance `r` from nucleous at which `e^(-)` finding probability is max. [For H-atom]`a_(0)rarrI` Bohr radius
View SolutionThe number of radial nodes and angular nodes for d-orbital can be represented as
View SolutionAccording to qauntum mechanical model of H-like species, and electron can be represented by a wave function `(psi)` which contain all dynamic information about the electron. The nature of wave function depends on the type of the orbital to which the electron belongs. For an orbital
`psi=[sqrt(2)/(81sqrt(3pi))]((1)/(a_(0)))^(3//2)(27-18sigma+2sigma^(2))e^((sigma)/(3))`
Where, `sigma =((Zr)/(a_(0))),r` = radial distance from nucleous, `a_(0)=52.9pm`
The orbital could possibly be
View SolutionFor a 3s-orbital
`Phi(3s)=(1)/(asqrt(3))((1)/(a_(0)))^(3//2)(6-6sigma+sigma^(2))in^(-sigma//2)`
where `sigma=(2rZ)/(3a_(sigma))`
What is the maximum radial distance of node from nucleus?
View SolutionHow many sub-shell are there in N shell? How many orbitals are there in d sub-shell?
View Solution`A` wave function for an atomic orbital is given as `Psi_(2,1,0)` Recogine the orbital
View SolutionState which of the following sets of quantum number would be possible and which would not be permisible for an electron in an atom.
(i) `n=3,I=3,m_(l)=+3, m_(s)=+(1)/(2)`
(ii) `n=3,I=3,m_(l)=+1, m_(s)=-(1)/(2)`
(iii) `n=5,I=4,m_(l)=+3, m_(s)=(1)`
(iv) `n=0,I=0,m_(l)=0, m_(s)=+(1)/(2)`
(v) `n=4,I=3,m_(l)=-2, m_(s)=-(1)/(2)`
View SolutionGive the sets of quantum number that describe an electron in a `3p` orbital
View SolutionWhat is the maximum number of electrons that can be accommodated :
(i) in the shell with `n=3`
(ii) in the subshell with `I=3`
(iii) in the orbital with `m_(I) = +3`
View SolutionWhich pf the following orbitals are not possible?
`2d,4f,4g` and `6d`
View Solution`A` electron can exist in bound system as well as an independent particle. Which quantum number is always associated with an electron ?
View SolutionWhat are the possible values of `l` for an electron with `n=3` ?
View SolutionWhat are the possible values of `m_(l)` for an electron with `l=2` ?
View SolutionWhat are possible values of `m_(s)` for an electron with `m_(l)=0` ?
View SolutionExplain the origin of term magnetic quantum number ?
View SolutionExplain the origin of term magnetic quantum number ?
View SolutionWhat is the angular momentum of an electron in `3P` orbital.
View SolutionWhat is spin angular momentum of an electron.
View SolutionThe angular momentum of electron in 3d orbital of an atom is
View SolutionWhat will be the orbital angular momentum of an electron in 2s-orbital?
View SolutionMatch the column : `{:(,"Column-I",,"Column-II",),(,("Quantum, no. of mono electron atom"),,("Quantisation of"),),((A),n,(P),"magnitude of orbital angular momentum",),((B),l,(Q),"energy & position",),((C),m,(R),"magnetic & direction of spin angular momentum",),((D),s,(S),"direction of orbital angular momentum",),(,,,,),(,,,,):}`
View SolutionWhat are the possible set of quantum number for highest energy electron (in ground state) for chlorine atom.
`{:(,n,l,m,),((A),2,0,0,),((B),2,1,-2,),((C),3,1,2,),((D),3,1,0,):}`
View SolutionThe electrons, identified by quantum number n and l
i. `n = 4,l=1` ii. `n = 4, l= 0` iii. `n = 3 , l= 2 ` iv. `n= 3 , l = 1`
Can be palced in the order of increasing energy from the lowest to highest,its
View SolutionA compound of vanadium has a magnetic moment of `1.73BM`. Work out the electronic configuration of vanadium in the compound
View SolutionCalculate distance of closet approach by an `alpha `-particle of `KE=2.5 MeV` being scattered by gold nucleus `(Z=79)`.
View Solution(a) Calculate `KE` of photoelectron emiited from sodium surface when light of wavelength `400nm` is incident on it (Work function of sodium `=2.28eV`).
(b) Calculate maximum wavelength (threshold wavelength) that can cause emission of photoelectron from sodim surface.
View Solution`0.24eV` of energy is required to stop photoelectron emitted by radiation of wavelength `2480 Å`. Find work function of metal used?
View SolutionCalculate no. of photons emitted by `60W` bulb in `10` hours that produces light of wavelength `6.626 Å`
View SolutionWhat maximum wavelength is required for a photon to dissociate : `X_(2)(g) rarr 2X(g)` if bond energy of `X-X` bond is `240kJ//mol` ?
View Solution`O_(2)` undergoes photochemical dissociation into one normal oxygen atom and one excited oxygen atom. Excited oxygen atom is `1.967 eV` more energetic than normal . The dissociation of `O_(2)` into two normal atoms of oxygen required `498 kJ mol^(-1)`, what is the maximum wavelength effective for photochemical dissociation of `O_(2)`?
View SolutionStopping potential [V volts] is plotted against frequancy of light used `[vec]`.
Find work function `(eV)`
_S01_084_Q01.png)
View Solution`A` light source of power 16 watts emits light of wavelength `310nm`. If all emitted photons are made to strike a metal plate of work function `1.5eV` then find out the magnetic of photo-current if `50%` of incident photons eject photoelectrons.
View Solution`A` vessel contains `X` moles of `H(g)` at P atm `&` T.K. If radiation is used to excite these H-atoms from ground state to nth excited state find total energy (in joules) required in form of radiations?
View SolutionPhotons of wavelength `lambda` are made incident on sample of diatomic gas `X_(2)`. If bond energy of `X-X` bond is `EkJ mol^(-1)`:
(a) Find critical value of `'lambda'` so as break `X-X` bond
(b) Assuming photons posses more energy than required to break the `X-X` bond, what X-then would be the KE per `X(g)` atom after the bond is broken ?
View SolutionThe period of revolution of an electron in the ground state of hydrogen atom is T. The period of revolution of the electron in the first excited state is
View SolutionFind radius
(A) `1^(st)` Bohr orbit of H-atom
(B) `2^(nd)` shell of `Li^(+2)` ion `(Z=3)`
(C ) `M` shell of `He^(+)` ion `(Z=2)`
View SolutionFind ratio of radius of `2^(nd)` orbit of `He^(+)` ion `& 3^(rd)` orbit of `Be^(+3)` ion.
View SolutionFind ratio of velocities of electrons in `2^(nd)` excited state of `Li^(+2)` ion `& 3^(rd)` excited state of H-atom.
View SolutionFind total energy, `PE & KE` of electron in :
(A) `2^(nd)` orbit of `He^(+)` ion.
(B) `1^(st)` excited state of `Be^(+3)` ion.
View SolutionAn excited `He^(+)` ion emits photon of wavelength `lambda` in returning to ground state from `n^(th)` orbit. If R is Rydberg's constant then :
View SolutionHow many unique spectral lines are emitted when `e^(-)` returns from `n_(2)^(th)` orbit to `n_(1)^(th)` orbit in a sample of H-like species ?
View SolutionIf electrons in H-likes species jump, from `n_(3)` to `n_(1)` emitting photon of wavelength `lambda`, from `n_(3)` to intermediate orbit `n_(2)[n_(3)gtn_(2)gtn_(1)]` emits photon with wavelength `lambda_(1)` & from `n_(2)` to `n_(1)` emits photon with wavelength `lambda_(2)` then correct option is :
View SolutionFind wavelength of `1^(st)` line of Paschen series of hydrogen spectrum.
View SolutionIf shortest wavelength of H-atom in Balmer series is X then
(i) What is the shortest wave length in Lyman series.
(ii) What is the longest wave length in Paschen series.
View Solution`A` H-like ion is observed to emit six different wavelength originating from all possible transitions between a group of levels. These levels have energies between `-0.85 eV` (Min) and `-0.544 eV` (Max)
(a) Find atmoic number (z) of element
(b) Find quantum number of levels between which transitions occur.
(c) Calculate largest wavelength emitted in transitions between the levels.
View SolutionThe radius of which of the following orbit is same as that of the first Bohr’s orbit of hydrogen atom?
View SolutionFind the wavelength of light emitted when an electron drops from `n=3` level to ground state in `He^(+)` ion Given Rydberg constant `=10^(7)m^(-1)`
View SolutionThe maximum number of electron that can be accommodated in `4^(th)` shell is.
View SolutionWrite the electronic configuration whose atomic number are `6,16,26,36,56`.
View SolutionThe less ground state electronic configeration of nitrogen atom can be represented by
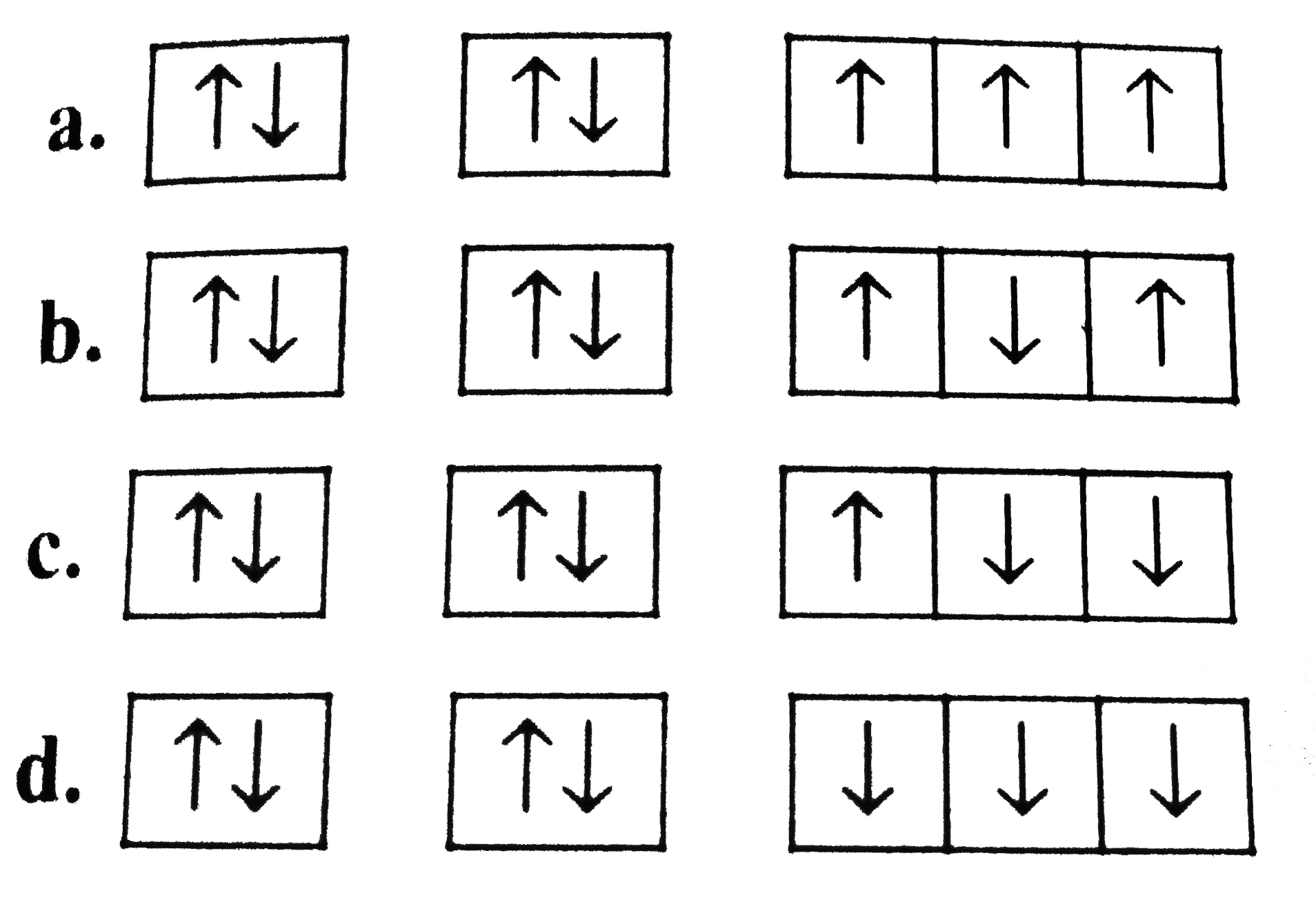
View Solution
Solved Example questions and complete solutions for chapter ATOMIC STRUCTURE of ALLEN of Class 11