Complete Solutions to Level 3 of chapter WORK AND ENERGY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK AND ENERGY |
| ANURAG MISHRA | Level 3 |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
In the shown figure, the spring and string is ideal. The spring the stiffness of `100 N//m` and `m = 1 kg` friction exists between mass 2m and surface with coefficient `mu = 0.8`. The system is released with spring from its relaxed position. Based on above data, answer the following question: (take `g = 10 m//s^(2)`)
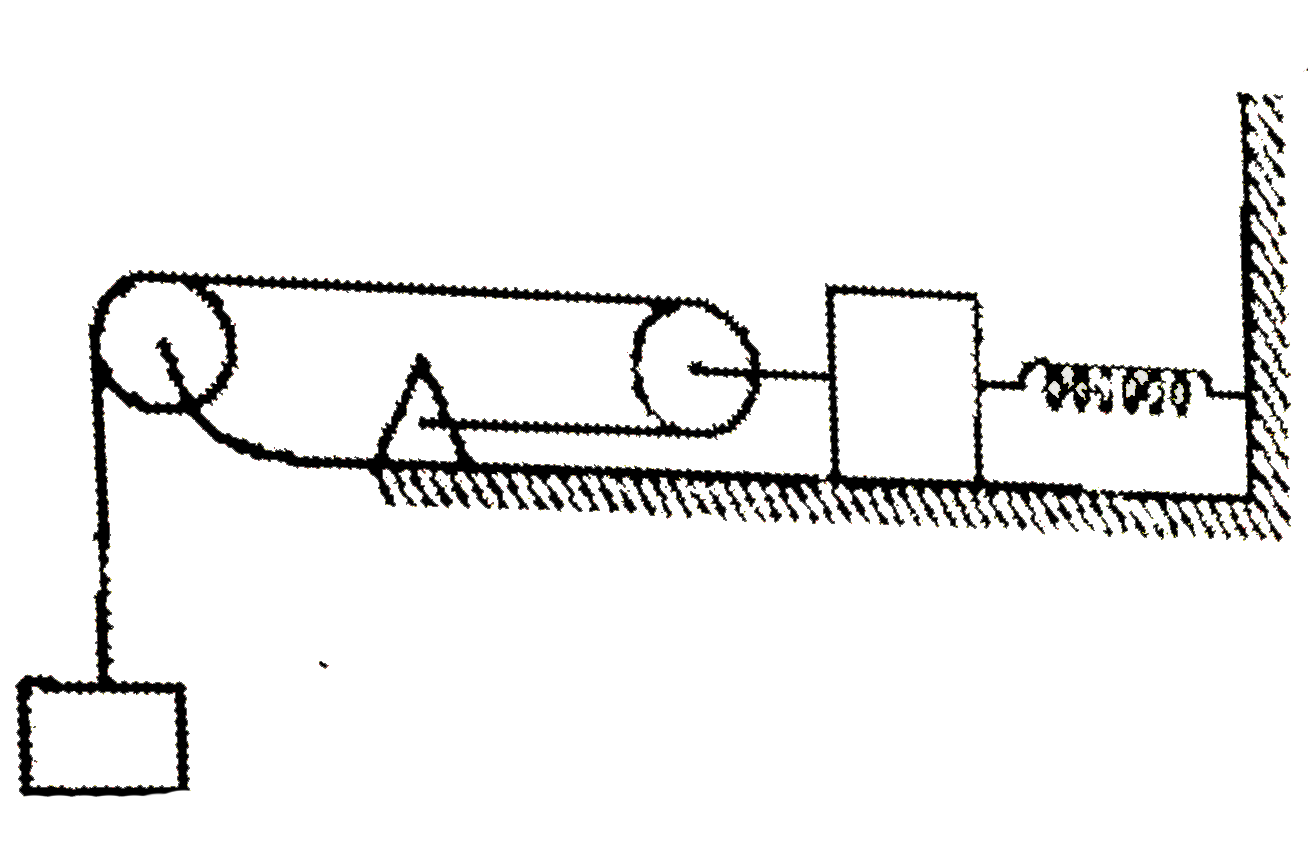
Maximum extension in spring is :
View SolutionIn the shown figure, the spring and string is ideal. The spring the stiffness of `100 N//m` and `m = 1 kg` friction exists between mass 2m and surface with coefficient `mu = 0.8`. The system is released with spring from its relaxed position. Based on above data, answer the following question: (take `g = 10 m//s^(2)`)

Magnitude of work done by gravity during the motion of system is :
View SolutionIn the shown figure, the spring and string is ideal. The spring the stiffness of `100 N//m` and `m = 1 kg` friction exists between mass 2m and surface with coefficient `mu = 0.8`. The system is released with spring from its relaxed position. Based on above data, answer the following question: (take `g = 10 m//s^(2)`)

Magnitude of net work done by spring after the system is released for motion is:
View SolutionIn the shown figure, the spring and string is ideal. The spring the stiffness of `100 N//m` and `m = 1 kg` friction exists between mass 2m and surface with coefficient `mu = 0.8`. The system is released with spring from its relaxed position. Based on above data, answer the following question: (take `g = 10 m//s^(2)`)
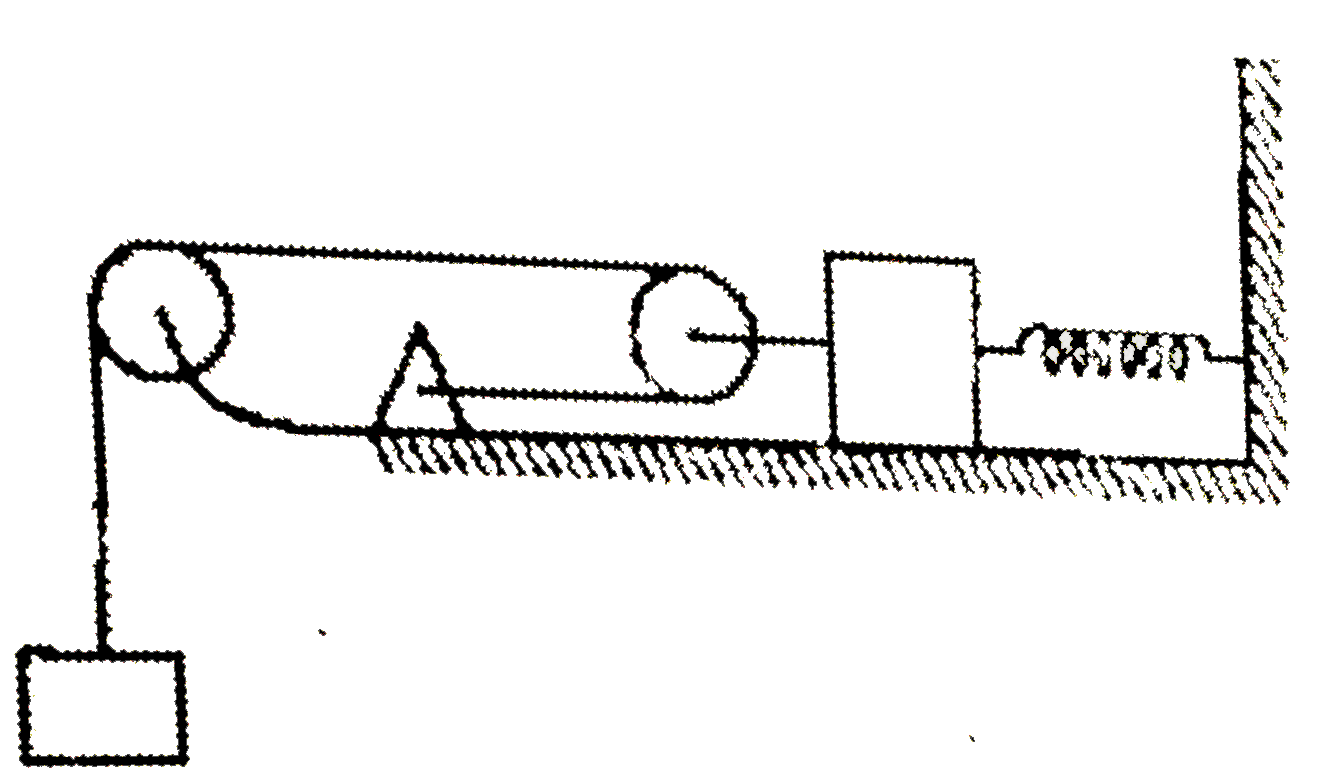
Frictional force acting on the mass 2m when it finally comes to rest is:
View SolutionIn the shown figure, the spring and string is ideal. The spring the stiffness of `100 N//m` and `m = 1 kg` friction exists between mass 2m and surface with coefficient `mu = 0.8`. The system is released with spring from its relaxed position. Based on above data, answer the following question: (take `g = 10 m//s^(2)`)
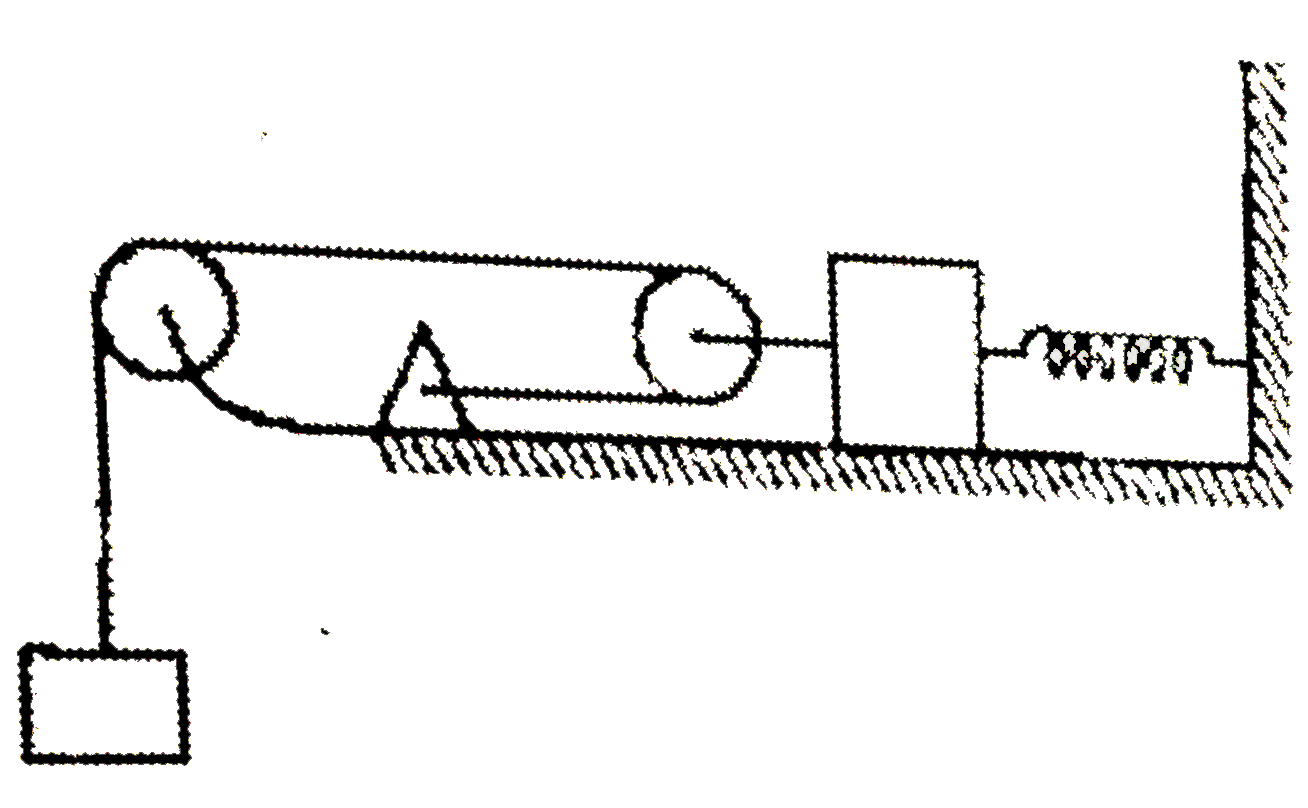
After what displacement of mass 2m, its velocity becomes maximum ?
View SolutionA single conservative force `F(x)` acts on a `1.0-kg` particle that moves along the x-axis. The potential energy `U(x)` is given by `U(x)=20+(x-2)^2` where x is in meters. At `x=5.0m`, the particle has a kinetic energy of `20J`.
What is the mechanical energy of a system?
View SolutionA single conservative `f_((x))` acts on a `m = 1 kg` particle moving along the x-axis. The potential energy `U_((x))` is given by :
`U_((x)) = 20 + (x - 2)^(2)`
where x is in metres. At `x = 5 m`, a particle has kintetic energy of 20 J
The maximum value of potential energy is:
View SolutionA single conservative `f_((x))` acts on a `m = 1 kg` particle moving along the x-axis. The potential energy `U_((x))` is given by :
`U_((x)) = 20 + (x - 2)^(2)`
where x is in metres. At `x = 5 m`, a particle has kintetic energy of 20 J
The maximum speed of the particle is:
View SolutionA single conservative `f_((x))` acts on a `m = 1 kg` particle moving along the x-axis. The potential energy `U_((x))` is given by :
`U_((x)) = 20 + (x - 2)^(2)`
where x is in metres. At `x = 5 m`, a particle has kintetic energy of 20 J
The minimum speed of the particle is:
View SolutionA single conservative `f_((x))` acts on a `m = 1 kg` particle moving along the x-axis. The potential energy `U_((x))` is given by :
`U_((x)) = 20 + (x - 2)^(2)`
where x is in metres. At `x = 5 m`, a particle has kintetic energy of 20 J
The maximum value of potential energy is:
View SolutionA single conservative `f_((x))` acts on a `m = 1 kg` particle moving along the x-axis. The potential energy `U_((x))` is given by :
`U_((x)) = 20 + (x - 2)^(2)`
where x is in metres. At `x = 5 m`, a particle has kintetic energy of 20 J
The least value of x (position of particle is ) will be:
View SolutionA single conservative `f_((x))` acts on a `m = 1 kg` particle moving along the x-axis. The potential energy `U_((x))` is given by :
`U_((x)) = 20 + (x - 2)^(2)`
where x is in metres. At `x = 5 m`, a particle has kintetic energy of 20 J
The largest value of x will be:
View SolutionA single conservative `f_((x))` acts on a `m = 1 kg` particle moving along the x-axis. The potential energy `U_((x))` is given by :
`U_((x)) = 20 + (x - 2)^(2)`
where x is in metres. At `x = 5 m`, a particle has kintetic energy of 20 J
The position of equilibrium and its nature is:
View SolutionA block of mass m moving with a velocity `v_(0)` on a smooth horizontal surface strikes and compresses a spring ofstiffuess k till mass coines to rest as shown in the figure. This phenomenon is observed by two observers :
(a) Standing on the horizontal surface
(b) standing on the block
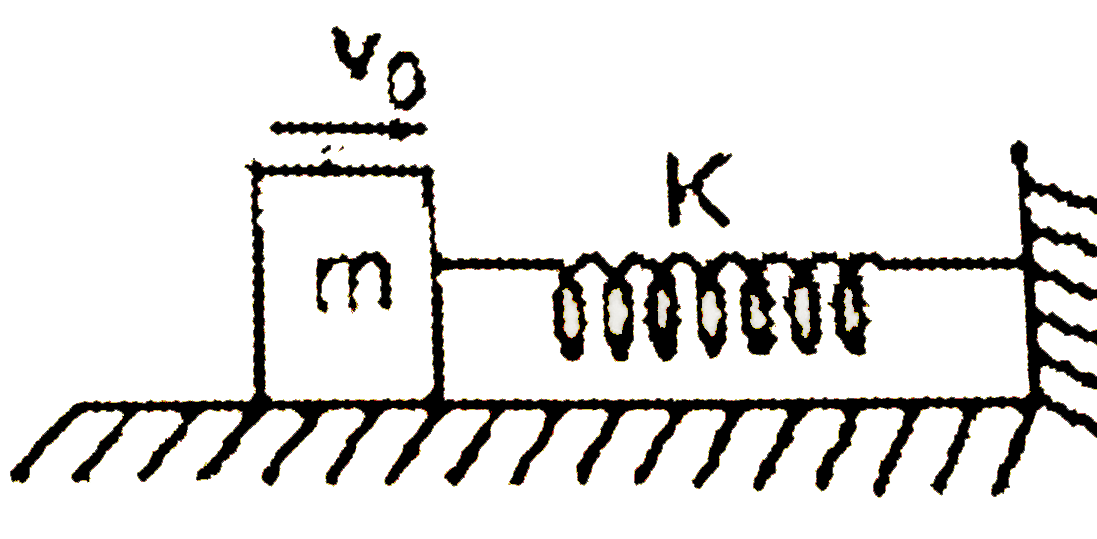
To an observer A the work done by spring force is:
View SolutionA block of mass m moving with a velocity `v_(0)` on a smooth horizontal surface strikes and compresses a spring ofstiffuess k till mass coines to rest as shown in the figure. This phenomenon is observed by two observers :
(a) Standing on the horizontal surface
(b) standing on the block
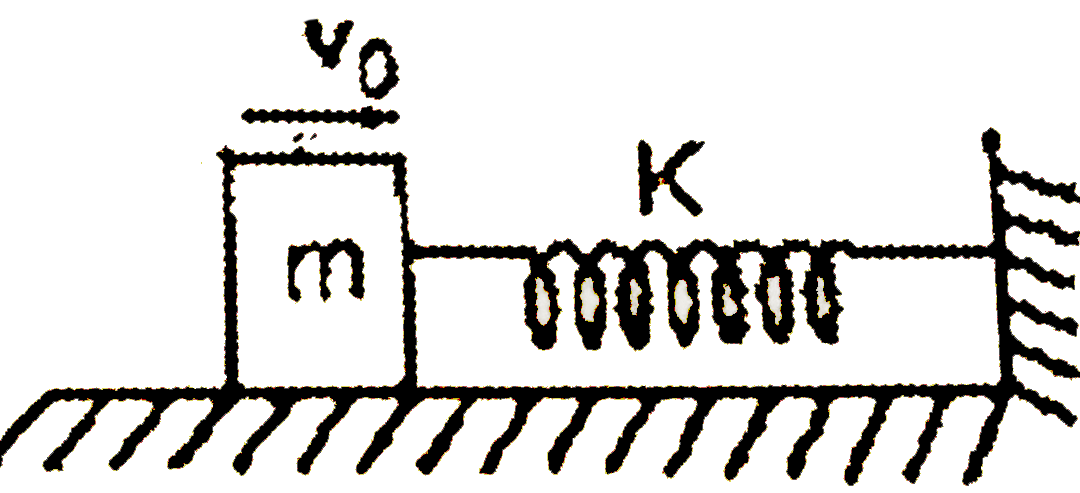
To an observer A, the work done by the normal reaction N between the block and the spring on the block is :
View SolutionA block of mass m moving with a velocity `v_(0)` on a smooth horizontal surface strikes and compresses a spring ofstiffuess k till mass coines to rest as shown in the figure. This phenomenon is observed by two observers :
(a) Standing on the horizontal surface
(b) standing on the block
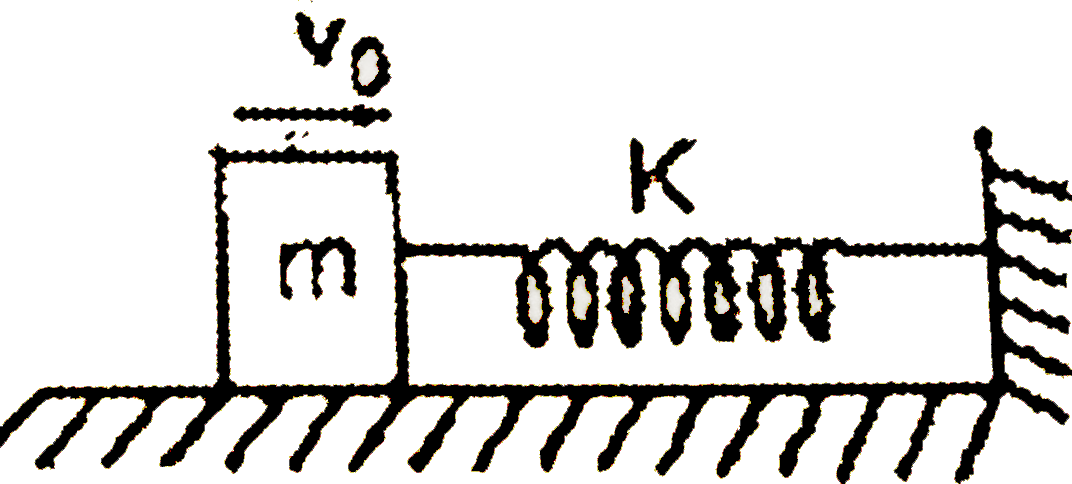
To an observer A, the net work done on the block is:
View SolutionA block of mass m moving with a velocity `v_(0)` on a smooth horizontal surface strikes and compresses a spring ofstiffuess k till mass coines to rest as shown in the figure. This phenomenon is observed by two observers :
(a) Standing on the horizontal surface
(b) standing on the block

Accoording to the observer A :
View SolutionA block of mass m moving with a velocity `v_(0)` on a smooth horizontal surface strikes and compresses a spring ofstiffuess k till mass coines to rest as shown in the figure. This phenomenon is observed by two observers :
(a) Standing on the horizontal surface
(b) standing on the block
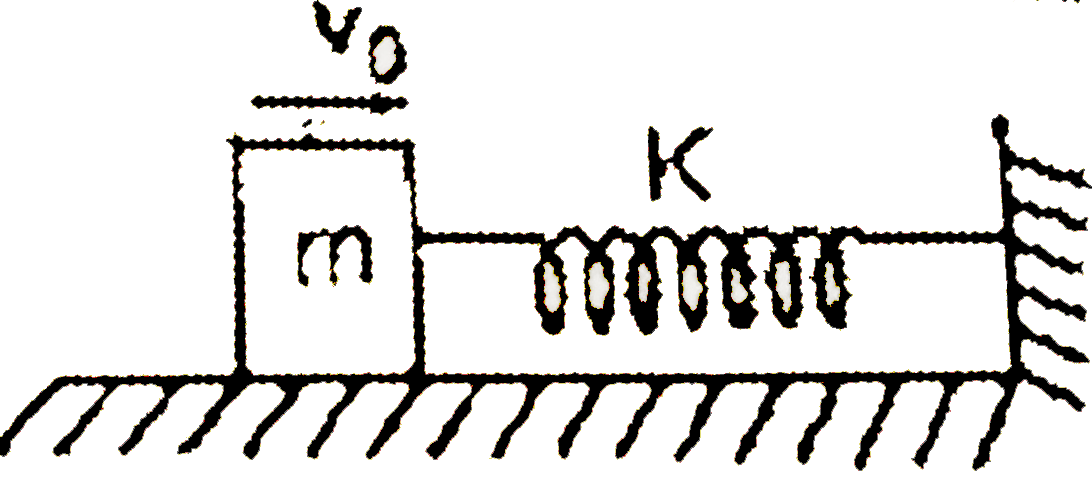
To an observer B, when the block is compressing the spring :
View SolutionA block of mass m moving with a velocity `v_(0)` on a smooth horizontal surface strikes and compresses a spring ofstiffuess k till mass coines to rest as shown in the figure. This phenomenon is observed by two observers :
(a) Standing on the horizontal surface
(b) standing on the block

According to observer B, the potential energy of the spring increases :
View SolutionA block of mass mis kept in an elevation which starts1 moving downward with an acceleration aas shown in figure. The block is observed by two observers A and B for a time interval `t_(0)`

The observer B finds that the work done by gravity on the block is :
View SolutionA block of mass mis kept in an elevation which starts1 moving downward with an acceleration aas shown in figure. The block is observed by two observers A and B for a time interval `t_(0)`

The observer B finds that the work done by pseudo-force on the block is :
View SolutionA block of mass mis kept in an elevation which starts1 moving downward with an acceleration aas shown in figure. The block is observed by two observers A and B for a time interval `t_(0)`
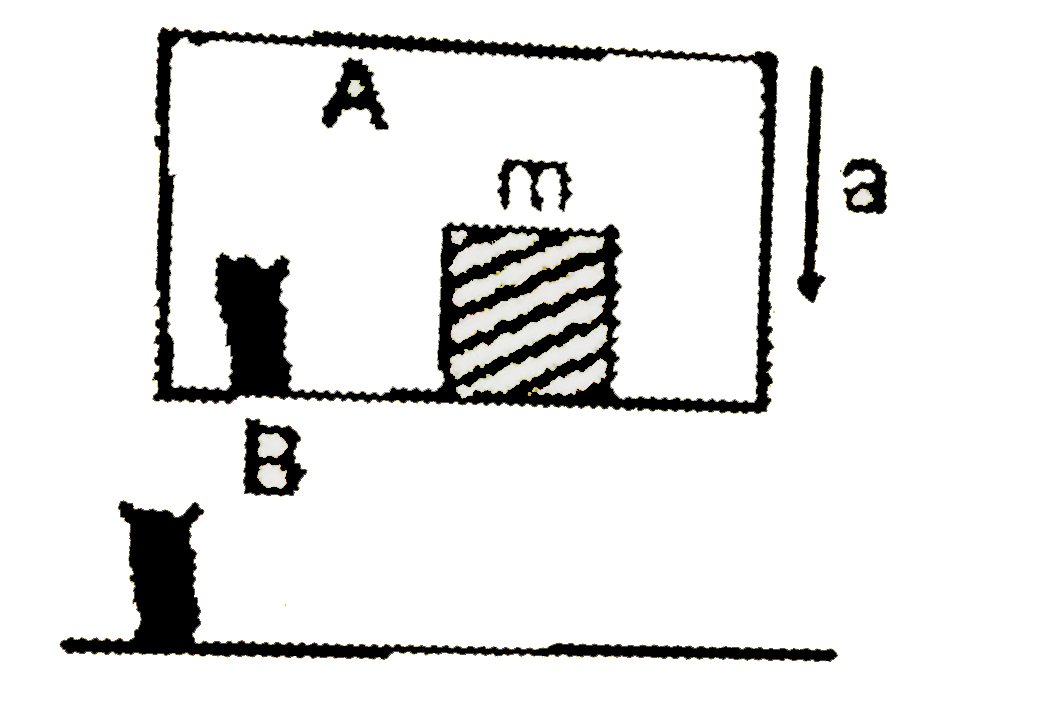
According to observer B, the net work done on the block is:
View SolutionA block of mass mis kept in an elevation which starts1 moving downward with an acceleration aas shown in figure. The block is observed by two observers A and B for a time interval `t_(0)`

According to the observer A :
View SolutionA spring block system is placed on a rough horizontal floor. The block is pulled towards right to give spring an eleongation less than `(2 mu mg)/(K)` but more than `(mu mg)/(K)` and released.

Which of the following Jaws/principles of physics can be applied on the spring block system ?
View SolutionA spring block system is placed on a rough horizontal floor. The block is pulled towards right to give spring an eleongation less than `(2 mu mg)/(K)` but more than `(mu mg)/(K)` and released.
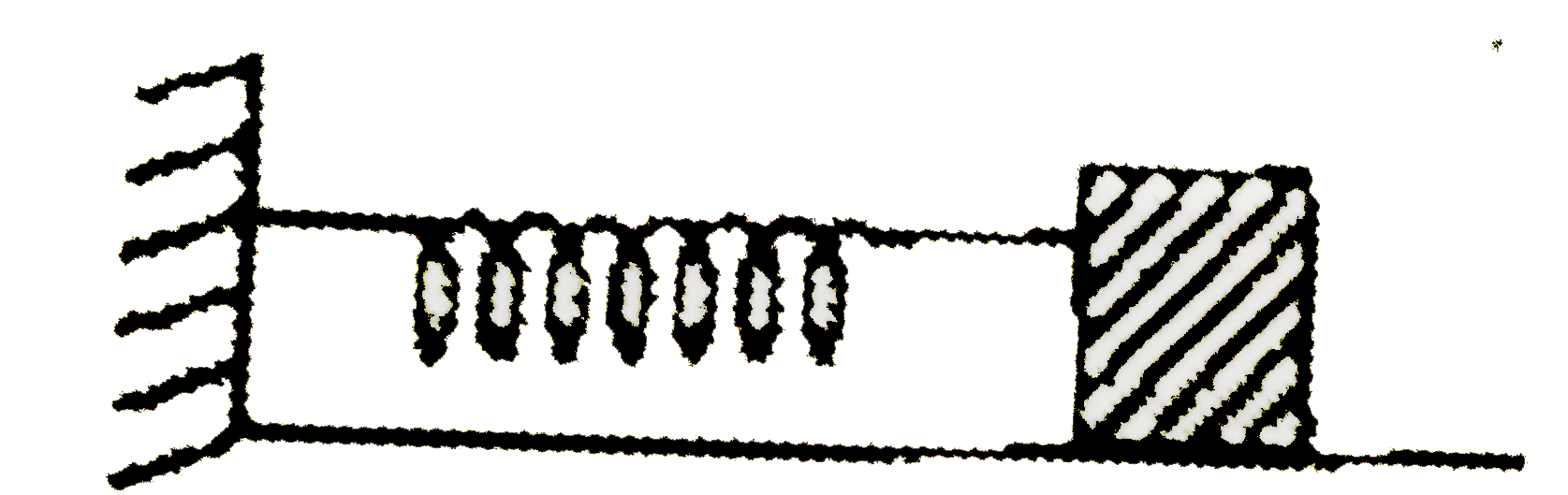
The correct statement is :
View SolutionThis diagram depicts a block sliding along a, frictionless ramp in vertical plane. The eightl numbered arrows in the diagram represent directions, to be referred to when answering the questions.
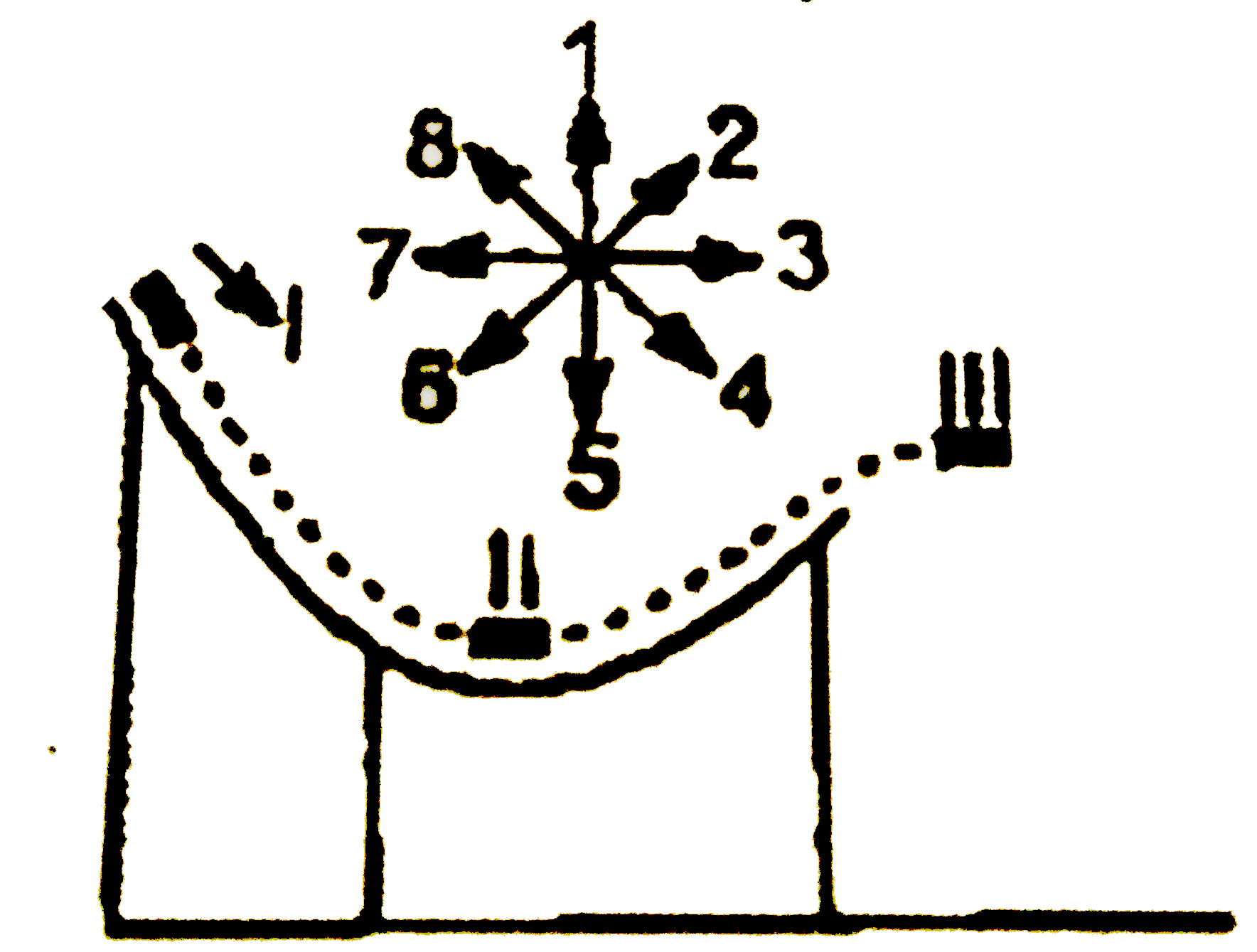
The direction of the acceleration of the block, when in position I, is best represented by which of the arrows in the diagram ?
View Solutionfigure depicts a block sliding along a frictionless ramp in vertical plane Eight numbered arrows in the diagram repreesent direction to be referred to when answering the questions
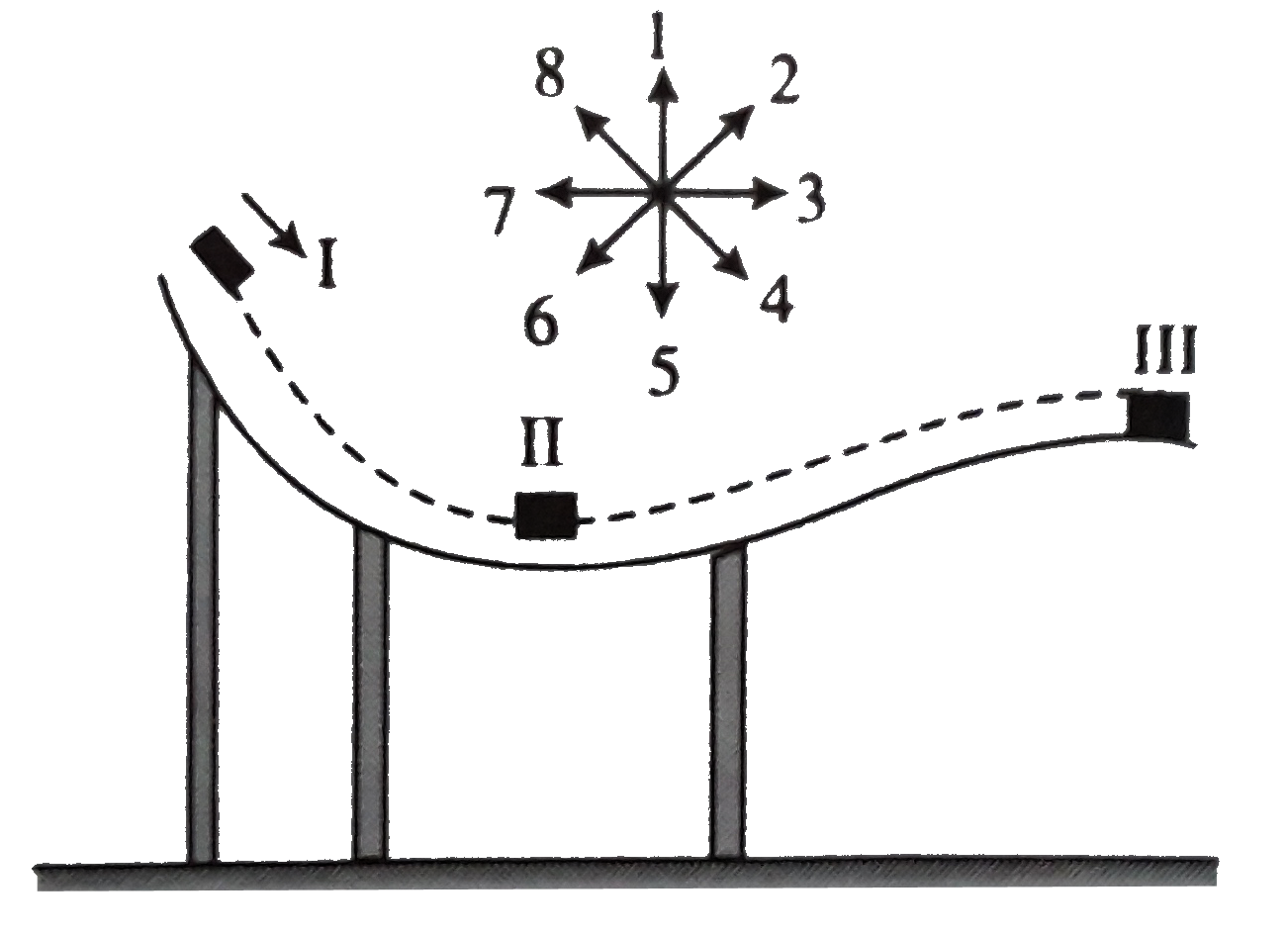
Position - i : Starts sliding on curve path
Position - ii : Lowest position of the curve path
Position - iii : Just outside of the curve path
The direction of the acceleration of the blocks when in position ii is best represented by which of the arrows in the diagram?
View SolutionThis diagram depicts a block sliding along a, frictionless ramp in vertical plane. The eightl numbered arrows in the diagram represent directions, to be referred to when answering the questions.

The direction of the acceleration of the block (after leaving the ramp) at position III is best represented by which of the arrows in the diagram ?
View SolutionThe kinetic energy of any body depends on the frame of reference of the observer. The kinetic energy is given by `1//2 mv_("rel")^(2)`. Similarly the displacement of the object from different frames of reference will be: different. But the forces acting on the body remain unchanged. So work done by the forces as seen from: different frames will be different. But work energy! theorem will still be hold in every inertial reference' frame.
For example, if a block of mass 2kg is moving with, velocity of `1m//s` towards east on a rough surface, its `KE = (1)/(2) xx 2 xx 1^(2) = 1J`
If it comes to rest, its `KE = 0`
work done by friction `= K_(f) - k_(i) = -1 J`
If we observe it form a frame 2 moving with `1m//s` toward east, its initial velocity will appear to be `1 - 1 = 0`
Initial `KE = (1)/(2) xx 2 xx 0^(2) = 0`
Final velocity `= 0 -1 = -1`
Final `KE = (1)/(2) xx 2 xx (-1)^(2) = 1J`
`rArr` Work done by friction `= 1 - 0 = 1J`
According to passage:
View SolutionThe kinetic energy of any body depends on the frame of reference of the observer. The kinetic energy is given by `1//2 mv_("rel")^(2)`. Similarly the displacement of the object from different frames of reference will be: different. But the forces acting on the body remain unchanged. So work done by the forces as seen from: different frames will be different. But work energy! theorem will still be hold in every inertial reference' frame.
For example, if a block of mass 2kg is moving with, velocity of `1m//s` towards east on a rough surface, its `KE = (1)/(2) xx 2 xx 1^(2) = 1J`
If it comes to rest, its `KE = 0`
work done by friction `= K_(f) - k_(i) = -1 J`
If we observe it form a frame 2 moving with `1m//s` toward east, its initial velocity will appear to be `1 - 1 = 0`
Initial `KE = (1)/(2) xx 2 xx 0^(2) = 0`
Final velocity `= 0 -1 = -1`
Final `KE = (1)/(2) xx 2 xx (-1)^(2) = 1J`
`rArr` Work done by friction `= 1 - 0 = 1J`
What should be the velocity of an observer so that he will report the work done by friction on the block to be 0:
View SolutionThe kinetic energy of any body depends on the frame of reference of the observer. The kinetic energy is given by `1//2 mv_("rel")^(2)`. Similarly the displacement of the object from different frames of reference will be: different. But the forces acting on the body remain unchanged. So work done by the forces as seen from: different frames will be different. But work energy! theorem will still be hold in every inertial reference' frame.
For example, if a block of mass 2kg is moving with, velocity of `1m//s` towards east on a rough surface, its `KE = (1)/(2) xx 2 xx 1^(2) = 1J`
If it comes to rest, its `KE = 0`
work done by friction `= K_(f) - k_(i) = -1 J`
If we observe it form a frame 2 moving with `1m//s` toward east, its initial velocity will appear to be `1 - 1 = 0`
Initial `KE = (1)/(2) xx 2 xx 0^(2) = 0`
Final velocity `= 0 -1 = -1`
Final `KE = (1)/(2) xx 2 xx (-1)^(2) = 1J`
`rArr` Work done by friction `= 1 - 0 = 1J`
Choose correct statement :
View SolutionThe potential energy at a point, relative to the reference point is always defined as the negative of work done by the force as the object moves from the reference point to the point considered. The value of potential energy at the reference point itself can be set equal to zero because we are always concerned only with differences of potential energy between two points and the associated change of kinetic energy. A particles A is fixed at origin of a fixed coordinate system. A particle B which is free to move experiences an force `vec(F) = (-(2a)/(r^(3)) + (beta)/(r^(2))) hat(r)` due to particle A where `hat(r)` is the position vector of particle B relative to A. It is given that the force is conservative in nature and _potential energy at infinity is zero. If B has to be removed from the influence of A, energy has to be supplied for such a process. The ionization energy E 0 is work that has to be done by an external agent to move the particle from a distance `r_(0)` to infinity slowly. Here `r_(0)` is the equilibrium position of the particle
What is potential energy function of particle as function of r.
View SolutionThe potential energy at a point, relative to the reference point is always defined as the negative of work done by the force as the object moves from the reference point to the point considered. The value of potential energy at the reference point itself can be set equal to zero because we are always concerned only with differences of potential energy between two points and the associated change of kinetic energy. A particles A is fixed at origin of a fixed coordinate system. A particle B which is free to move experiences an force `vec(F) = (-(2a)/(r^(3)) + (beta)/(r^(2))) hat(r)` due to particle A where `hat(r)` is the position vector of particle B relative to A. It is given that the force is conservative in nature and _potential energy at infinity is zero. If B has to be removed from the influence of A, energy has to be supplied for such a process. The ionization energy E 0 is work that has to be done by an external agent to move the particle from a distance `r_(0)` to infinity slowly. Here `r_(0)` is the equilibrium position of the particle
Find the ionization energy `E_(0)` of the particle B
View SolutionThe potential energy at a point, relative to the reference point is always defined as the negative of work done by the force as the object moves from the reference point to the point considered. The value of potential energy at the reference point itself can be set equal to zero because we are always concerned only with differences of potential energy between two points and the associated change of kinetic energy. A particles A is fixed at origin of a fixed coordinate system. A particle B which is free to move experiences an force `vec(F) = (-(2a)/(r^(3)) + (beta)/(r^(2))) hat(r)` due to particle A where `hat(r)` is the position vector of particle B relative to A. It is given that the force is conservative in nature and _potential energy at infinity is zero. If B has to be removed from the influence of A, energy has to be supplied for such a process. The ionization energy E 0 is work that has to be done by an external agent to move the particle from a distance `r_(0)` to infinity slowly. Here `r_(0)` is the equilibrium position of the particle
If particle B is transferred slowly from point `P_(1) (sqrt2 r_(0), sqrt2 r_(0))` to point `P_(2) ((r_(0))/(sqrt2), (r_(0))/(sqrt2))` in the xy-plane by an external agent, calculate work required to be done by it in the process:
View Solution
Level 3 questions and complete solutions for chapter WORK AND ENERGY of SHREE BALAJI PHYSICS (HINGLISH) of Class 11