Complete Solutions to Eample of chapter WORK AND ENERGY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK AND ENERGY |
| ANURAG MISHRA | Eample |
| Number Of Questions | 47 |
| Academic Year | 2023-24 |
An object is displaced from position vector `vec(r)_(1) = (2 hat(i) + 3 hat(j)) m` to `vec(r)_(2) == (4 hat(j) + 6 hat(k))m` under a force `vec(F) = (3 x^(2) hat(i) + 2y hat(j)) N`. Find the. work done this force.
View SolutionAn object is displaced from point `A(2m,3m,4m)` to a point `B(1 m,2 m,3 m)` under a constant force ` F=(2hati + 3hatj + 4hatk)N`. Find the work done by this force in this process.
View SolutionA block is being pulled slowly along a frictionless incline1 , [Fig. 3E. .3(a}.
( a) Show that the gravitationalforce is conservative . .
(b) Now.consider the incline tb be rough to show that frictional force is non-conservative...
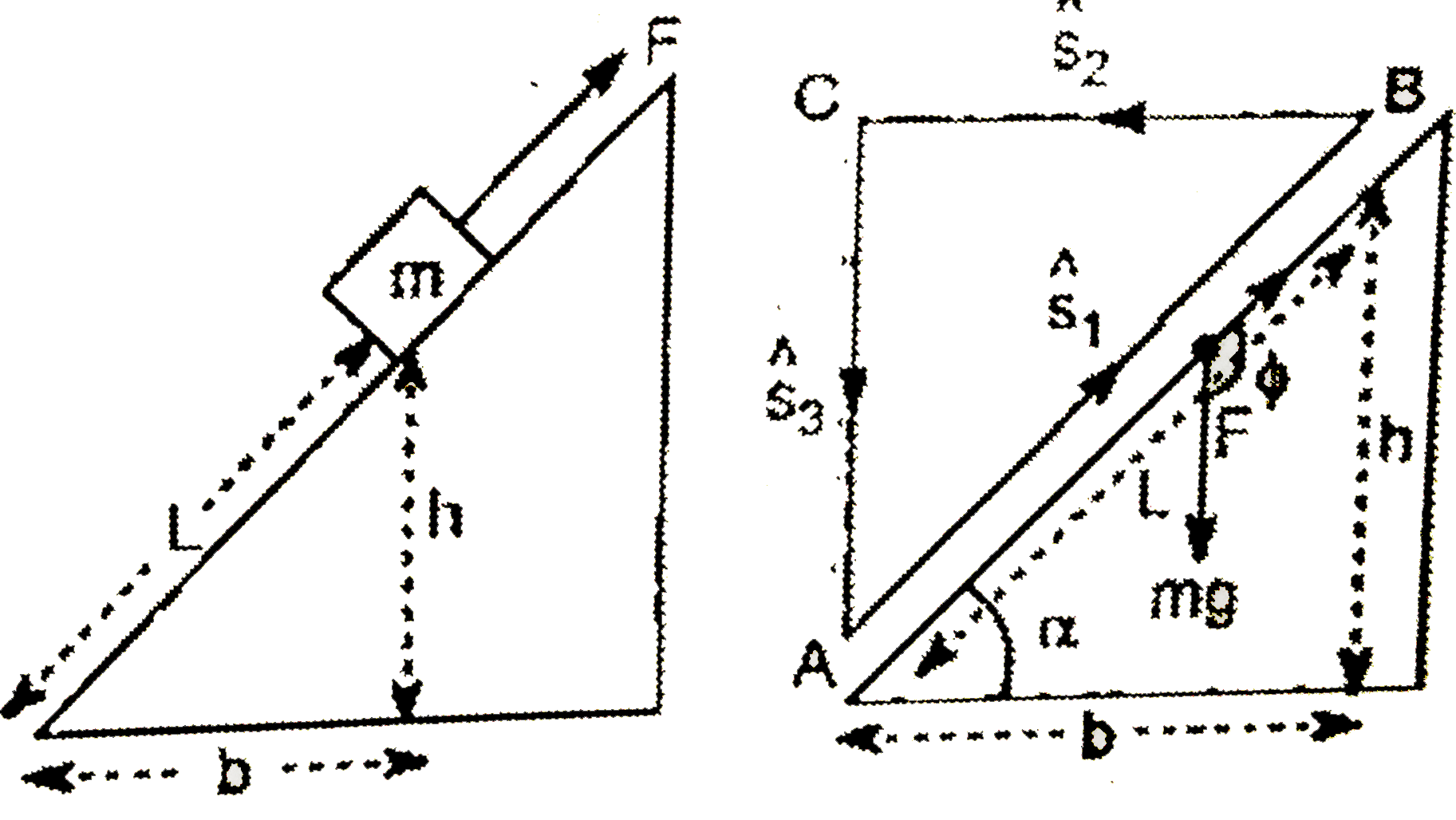
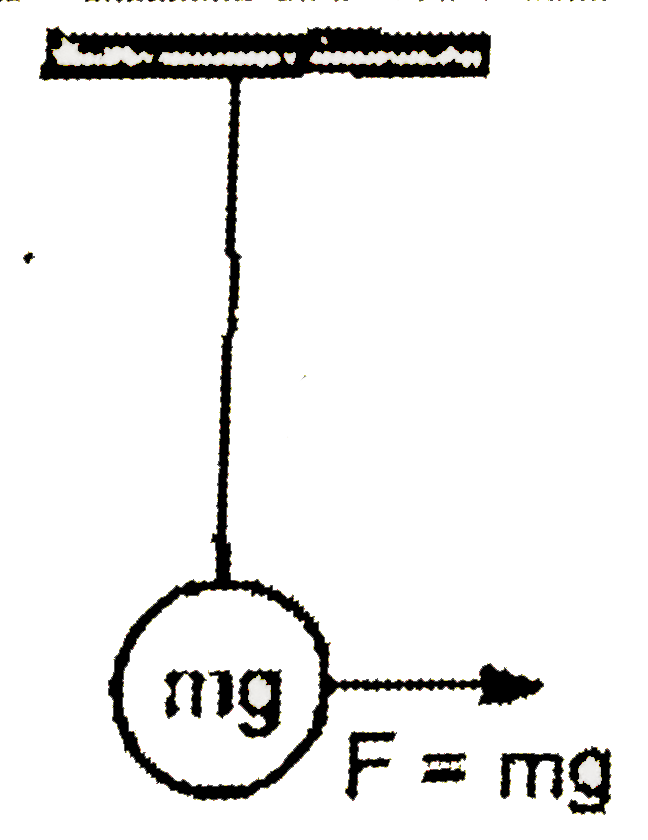
View SolutionA pendulum bob of mass m is suspended at rest. A constant horizontal force `F = mg` starts acting on it. Find
(a) the maximum angular defection of the string.
(b) the maximum possible tension in the string.
View SolutionUnder the action of a force, a `2 kg` body moves such that its position x as a function of time is given by `x =(t^(3))/(3)` where x is in metre and t in second. The work done by the force in the first two seconds is .
View SolutionA force of `(3 hat(i) - 1.5 hat(j)) N` acts on 5 kg body. The body is at a position of `(2 hat(i) - 3 hat(j)) m` and is travelling at `ms^(-1)`. The focce acts on the body until it is at the position `(hat(i) + 5 hat(j)) m`. Assuming no other force does work on the body, the final speed of the body.
View SolutionA spring block system is placed on a rough horizontal surface having coefficient of friciton `mu`. The spring is given initial elongation `3mumg//k` (where m=mass of block and k=spring constant) and the block is released from rest. For the subsequent motion, find
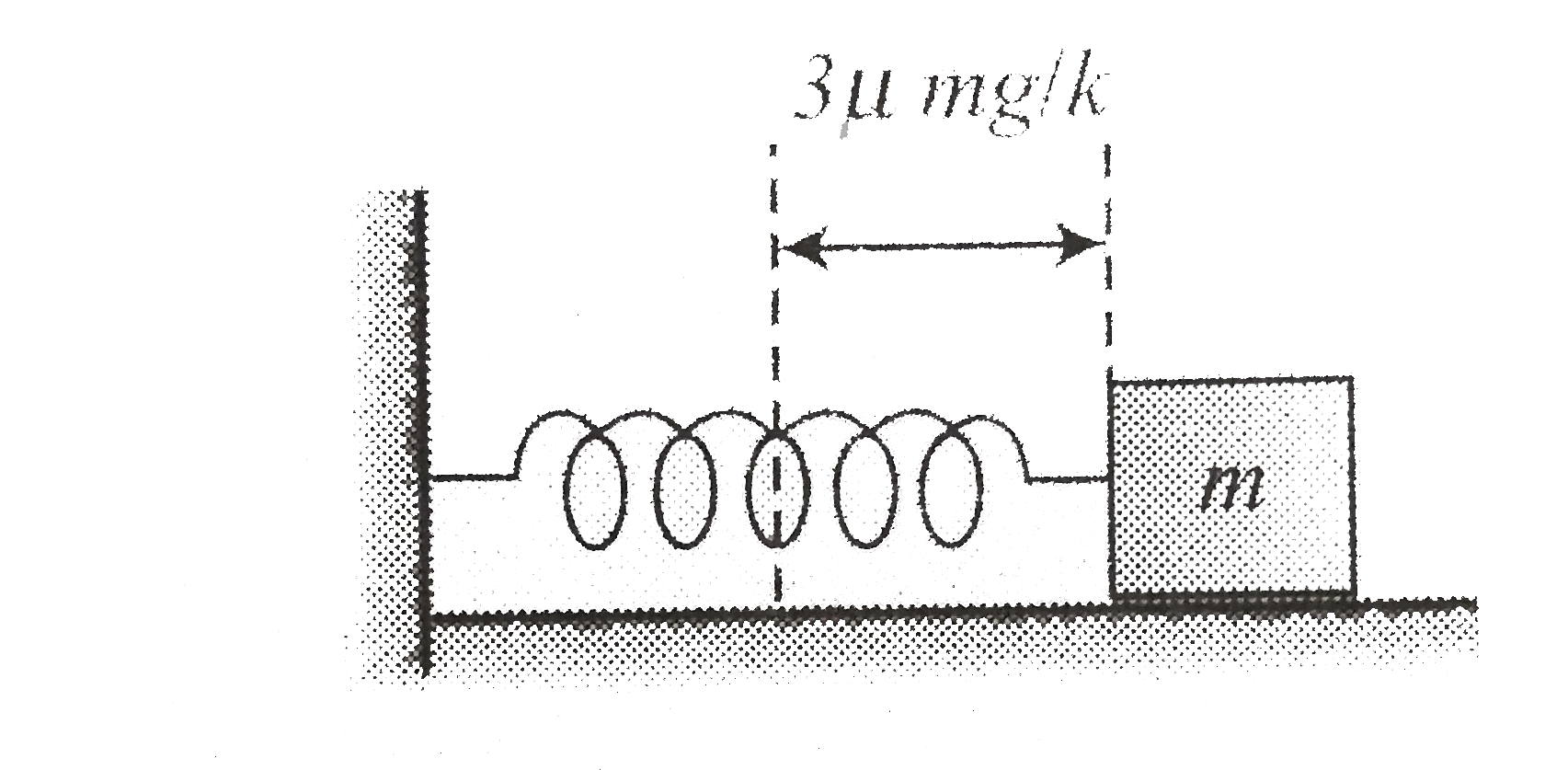
a. Initial acceleration of block
b. Maximum compression in spring
c. Maximum speed of the block
View SolutionIn the figure shown, the mass of the hanging block is m, while that of the black resting on the floor is 3m. The floor is horizontal and frictionless and all pulleys ideal. The system is initially held stationary with the inclined thread making an angle `theta = 30^(@)` with the horizontal. The blocks are now released from rest and allowed to move. the hanging block falls through a height (49.5) m before hitting the floor. it is found that the value of `theta` becomes `60^(@)`, when the hanging block hits the floor. Find the speed with which the hanging block hits the floor.

View SolutionTwo blocks having masses `8 kg` and 16 kg are connected to the two ends of a light spring. The system is placed on a smooth horizontal floor. An inextensible starting also connects B with ceiling as shown in figure at the initial moment. Initially the spring has its natural length. A constant horizontal force F is applied to the heavier block as shown. What is the maximum possible value of F so the lighter block doesn't loose contant with ground
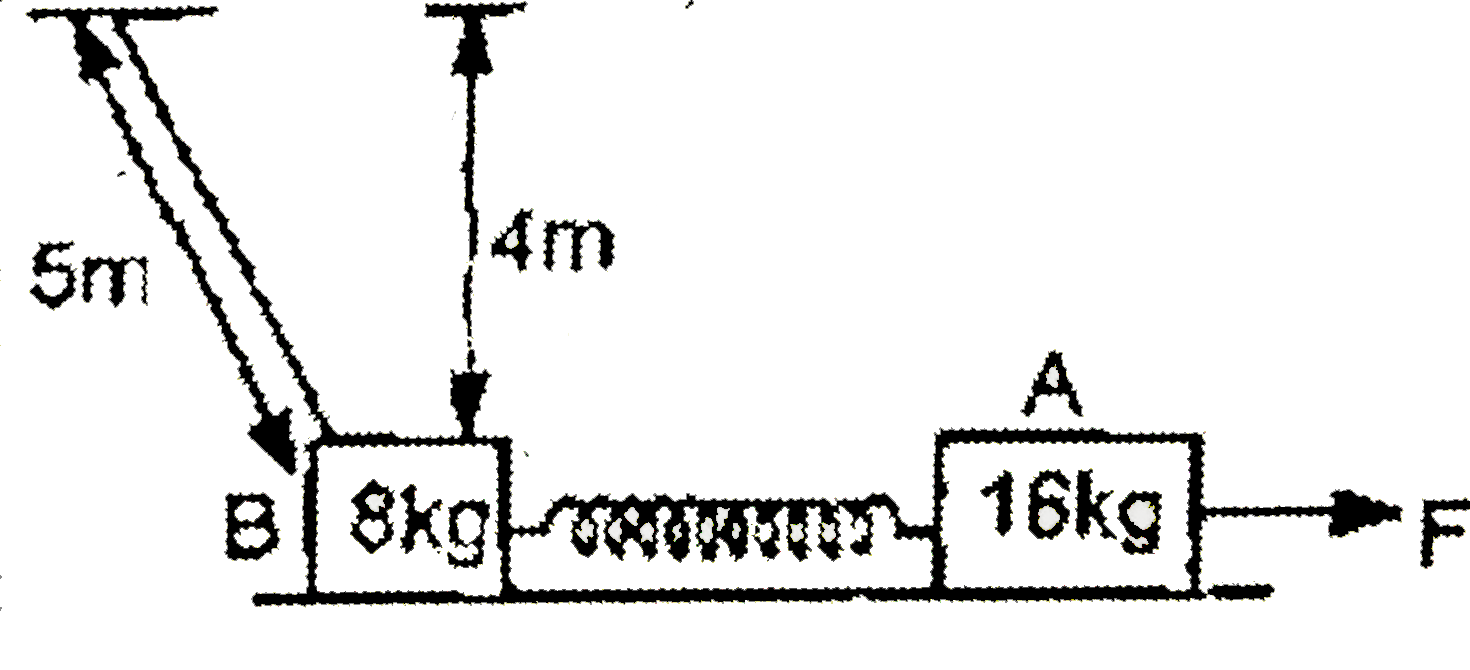
View Solutiona. A `2-kg` situated on a smooth fixed incline is connected to a spring of negligible mass, with spring constant `k=100Nm^-1`, via a frictionless pulley. The block is released from rest when the spring is unstretched. How far does the block moves down the incline before coming (momentarily) to rest? What is its acceleration at its lower point?
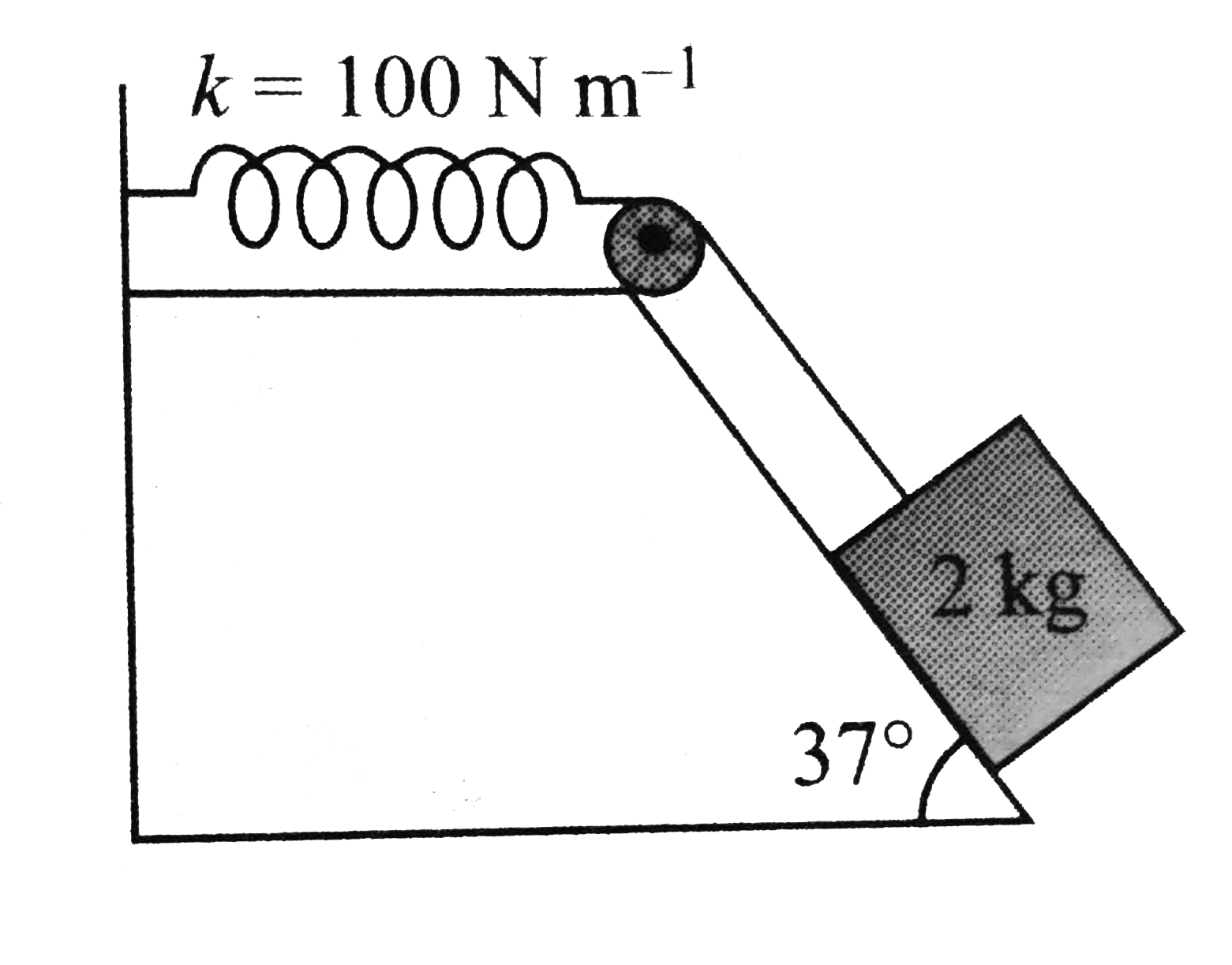
b. The experiment is repeated on a rough incline. If the block is observed to move `0.20m` down along the incline before it comes to instantaneous rest, calculate the coefficient of kinetic friction.
View SolutionA ring of mass `m=1kg` can slide over a smooth vertical rod. A light string attached to the ring passing over a smooth fixed pulley at a distance of `L=0.7m` from the rod as shown in figure.
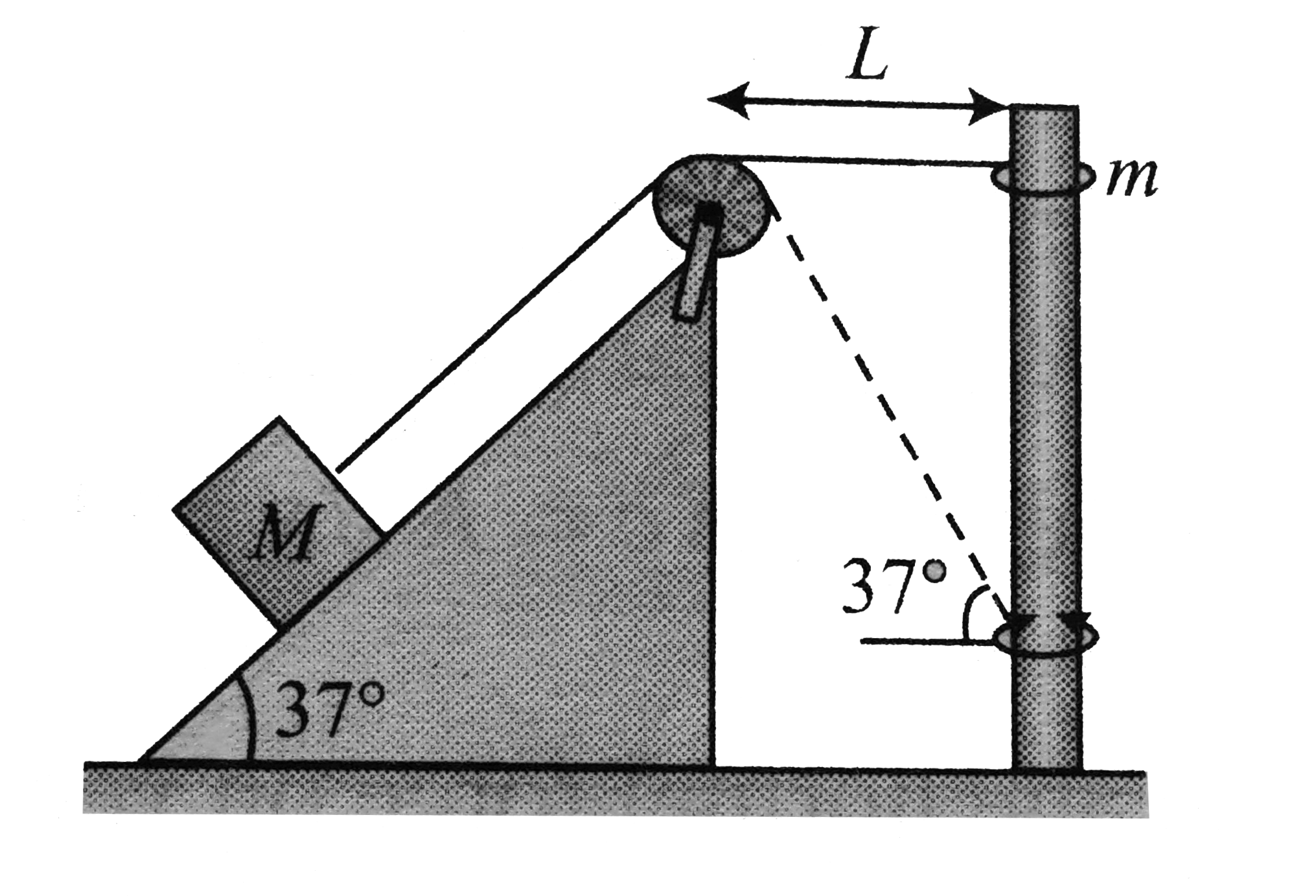
At the other end of the string mass `M=5kg` is attached, lying over a smooth fixed inclined plane of inclination angle `37^@`. The ring is held in level with the pulley and released. Determine the velocity of ring when the string makes an angle `(alpha=37^@)` with the horizontal. `[sin 37^@=0.6]`
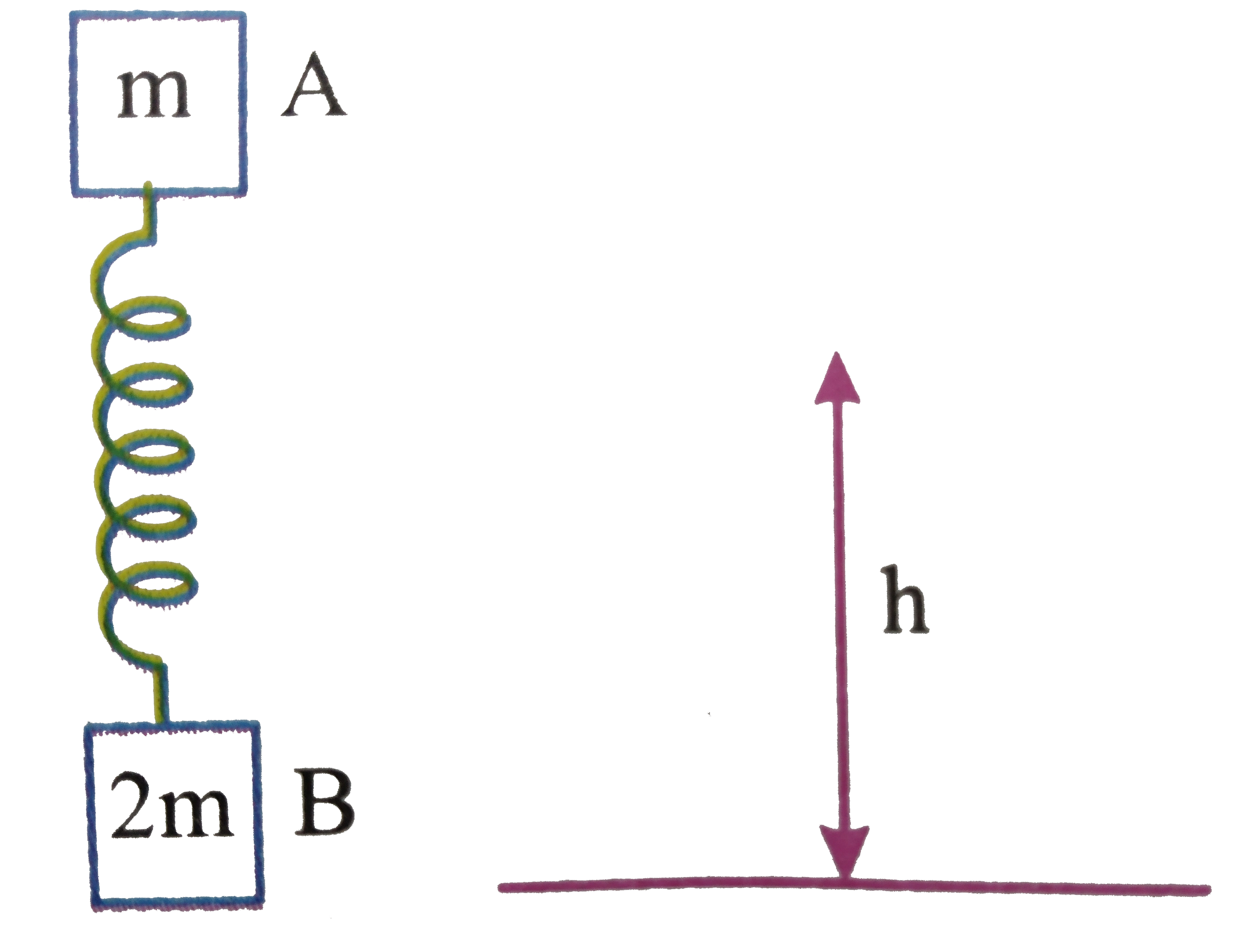
View SolutionFrom what minimum height `h`must the system be released when spring is unstretches so that after perfectly inelastic collision `(e =0)` with ground, `B` may be lifted off the gound: (Spring constant `=k)`
View SolutionA pendulum bob of mass m and length L is released from angle `theta` with the vertical. Find
(a) the speed of the bob at the bottom of the swing and
(b) tension in the string at that time
View SolutionA boy throws a ball with initial velocity `u` at an angle of projection `theta` from a tower of height H.
Neglecting air resistance, find
a. How high above the building the ball rises
b. Its speed just before it hits the ground.
View SolutionConsider an Atwood machine with both the masses at the same level as shown in Fig. 3E.15. Use the principle of conservation of energy to find
(a) speed of either of the masses as a function of its position and
(b) the acceleration of either of the masses.

View SolutionA block of mass m hangs an a vertical spring. Initially the spring is unstretched, it is now allowed to fall from rest. Find
(a) the distance the block falls if the block is released slowly,
(b) the maximum distance the block falls before it begins to move up
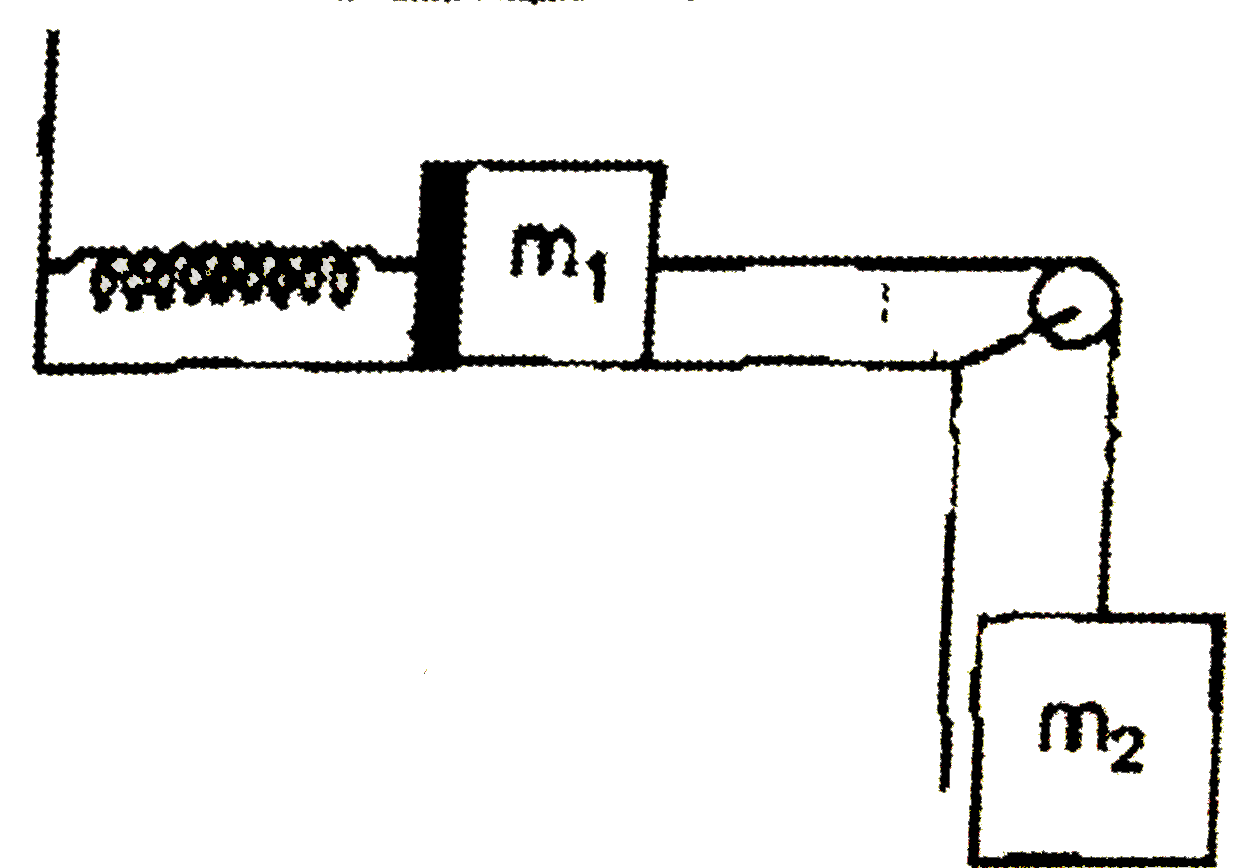
View SolutionIn Fig 3E.17, the mass `m_(2)` rests on a rough table. The mass `m_(1)` is pushed against the spring to which it is not attached Force constant of the spring is k, coefficient of friction is `mu_(k)`.
(a) Find the speed of the blocks after the spring is released and `m_(2)` has fallen a distance of `h`.
(b) If the spring is attached to the block and it falls a distance `h` before coming to rest, calculate the coefficient of friction `mu_(k)`.
View SolutionThe force 15 N pulls the lower block for 2m, find speed.

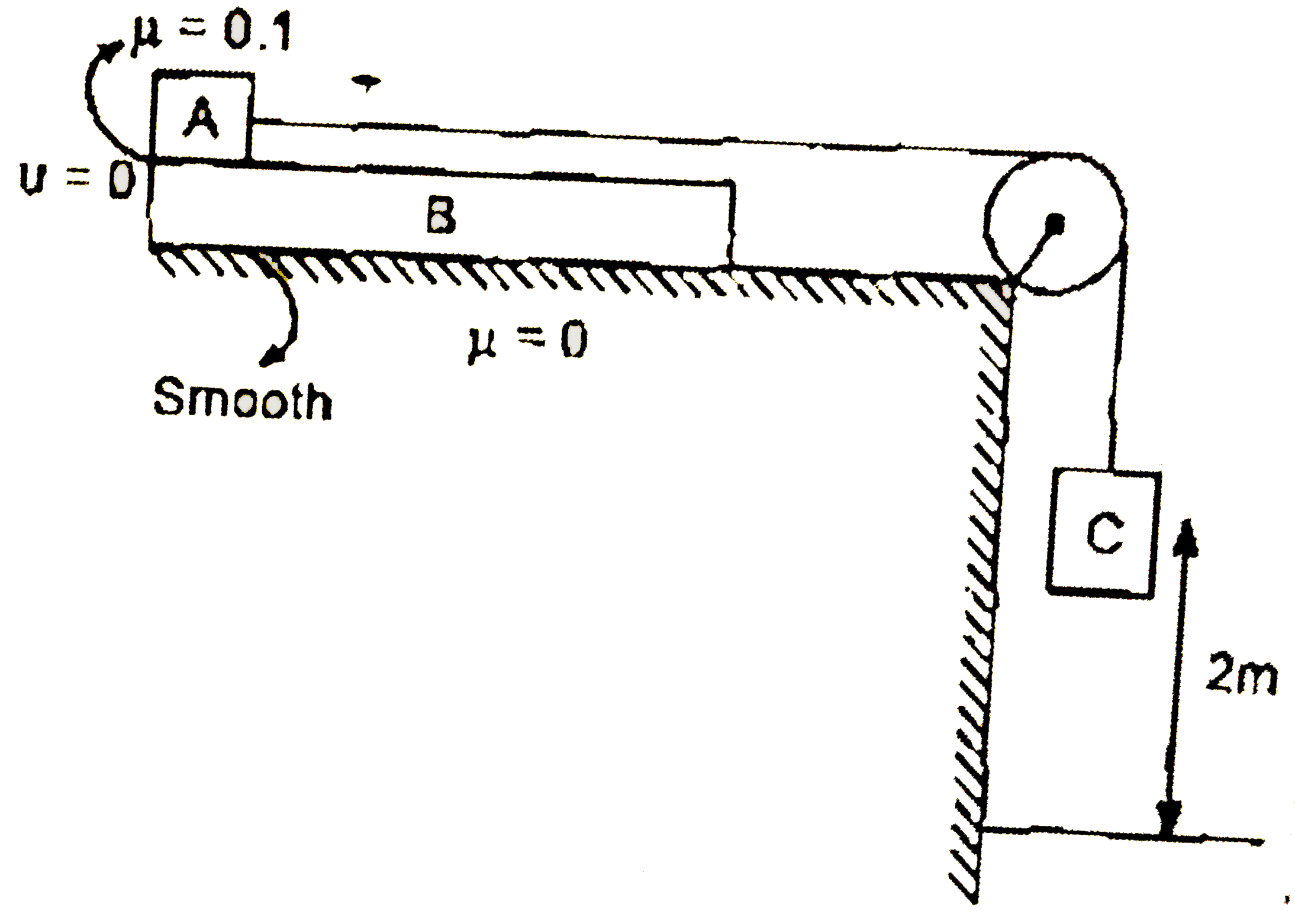
View SolutionFind velocity of A and B when A is about to touch the ground Also verify that work done by tension on the whole system and N between A and B is zero

View Solution`m_(A) = 1 kg, m_(B) = 2 kg, m_(C) = 10 kg`
View SolutionIf chain starts slipping find its KE when chain becomes completely straingt.
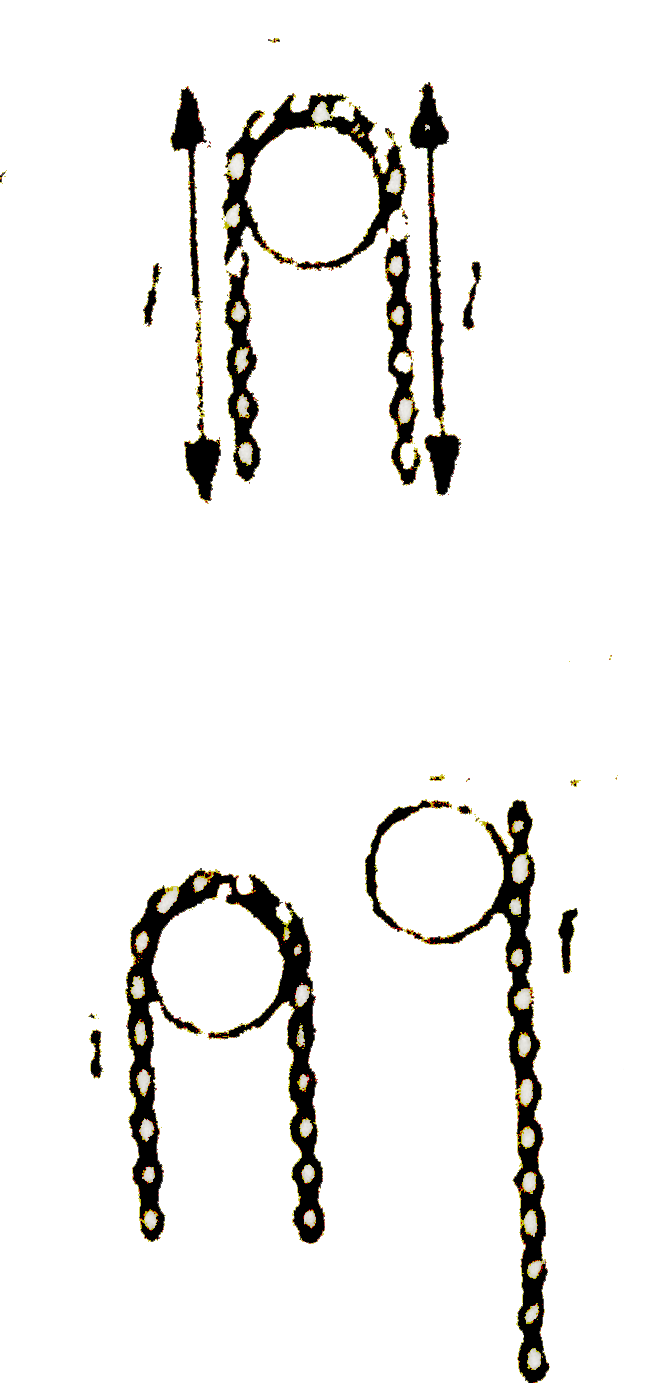
View SolutionChain is on the verge of slipping, find the velocity of the chain, when it has slipped.
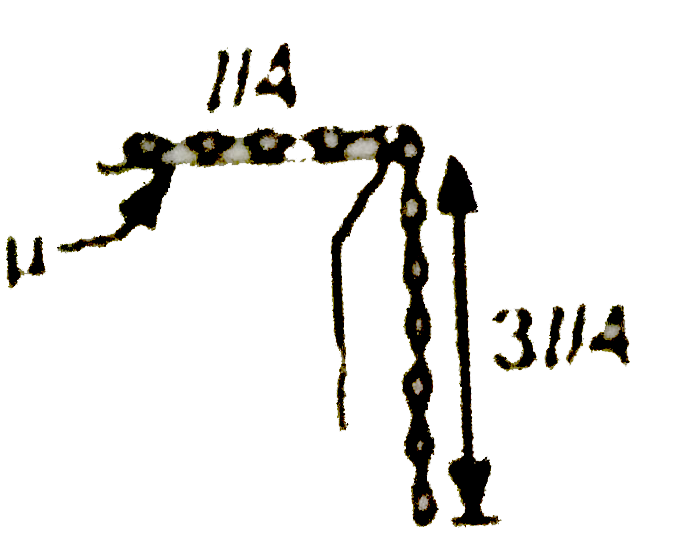
View SolutionFind how much m will rise if 4m falls away. Block are at rest and in equilibrium.
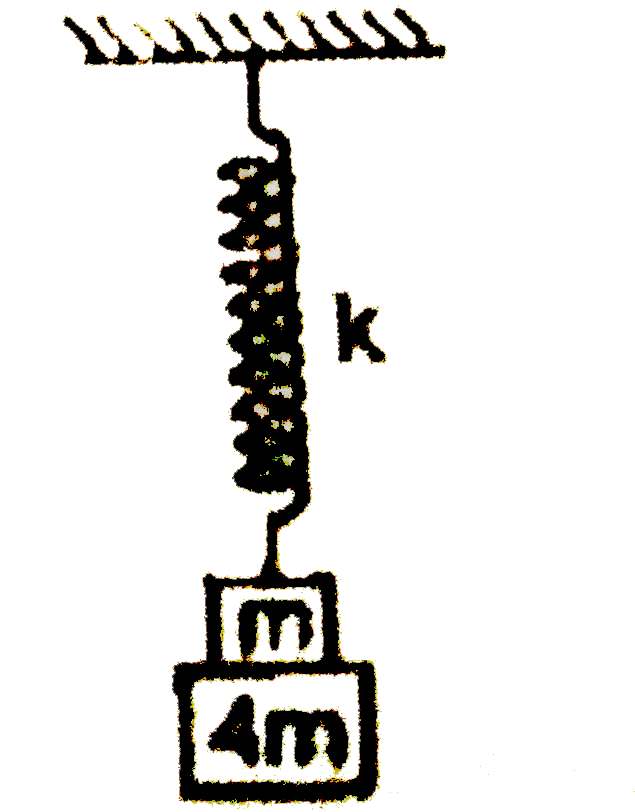
View SolutionFind velocity of ring when spring becomes horizontal

View SolutionA chain of mass m and length 1 lies on a rough table. The chain just starts to slip when the overhaning part equals `n^(th)` fraction of the chain length. If the chain is slightly distributed so that it completely slips off the table, what is the work performed by the friction forces.
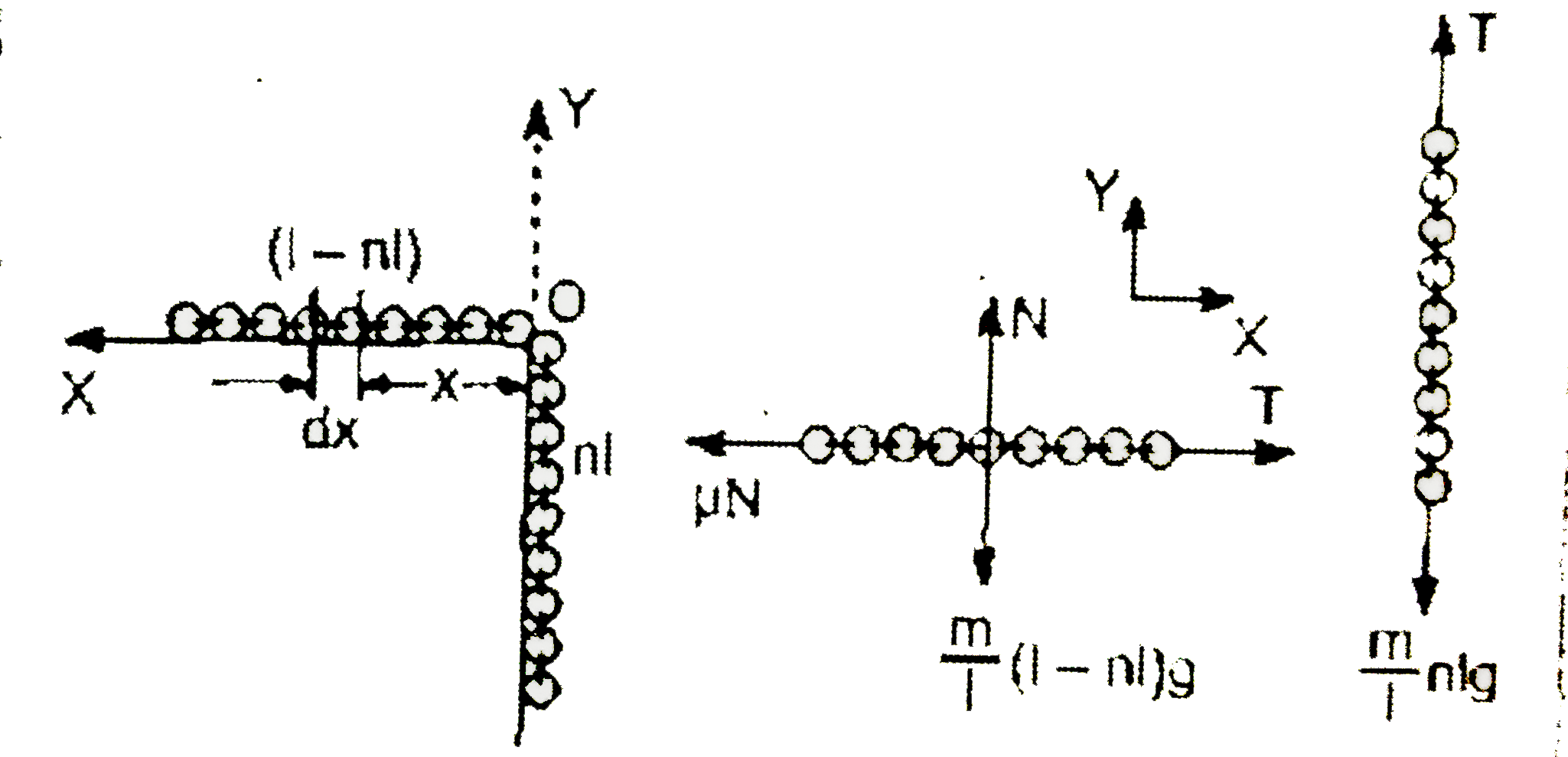
View SolutionA uniform chain of length 1 and mass m is kept on a smooth table. It is released from rest when the overhaning part was `n^(th)` fraction of total length. Find the kinetic energy of the chain as it completely slips off the table
View SolutionA uniform chain of length of length `pir` lies inside a smooth semicircular tube (AB) of radius r. Assuming a slight disturbance to start the chain in motion, the velocity with which it will emerge from the end `(B)` of the tube will be

View SolutionA uniform chain of mass `m` and length `llt(piR)/(2)` is placed on a smooth hemisphere of radius `R` with on of its ends fixed at the top of the sphere.
(a) Find the gravitational potential energy of chain assuming base of hemisphere as reference.
(b) what will be the tangential acceleraion of the chain when it starts sliding down.
(c ) If the chain slides down the sphere, find the kinetic energy of the chain when it has slipped through an angle `beta`.
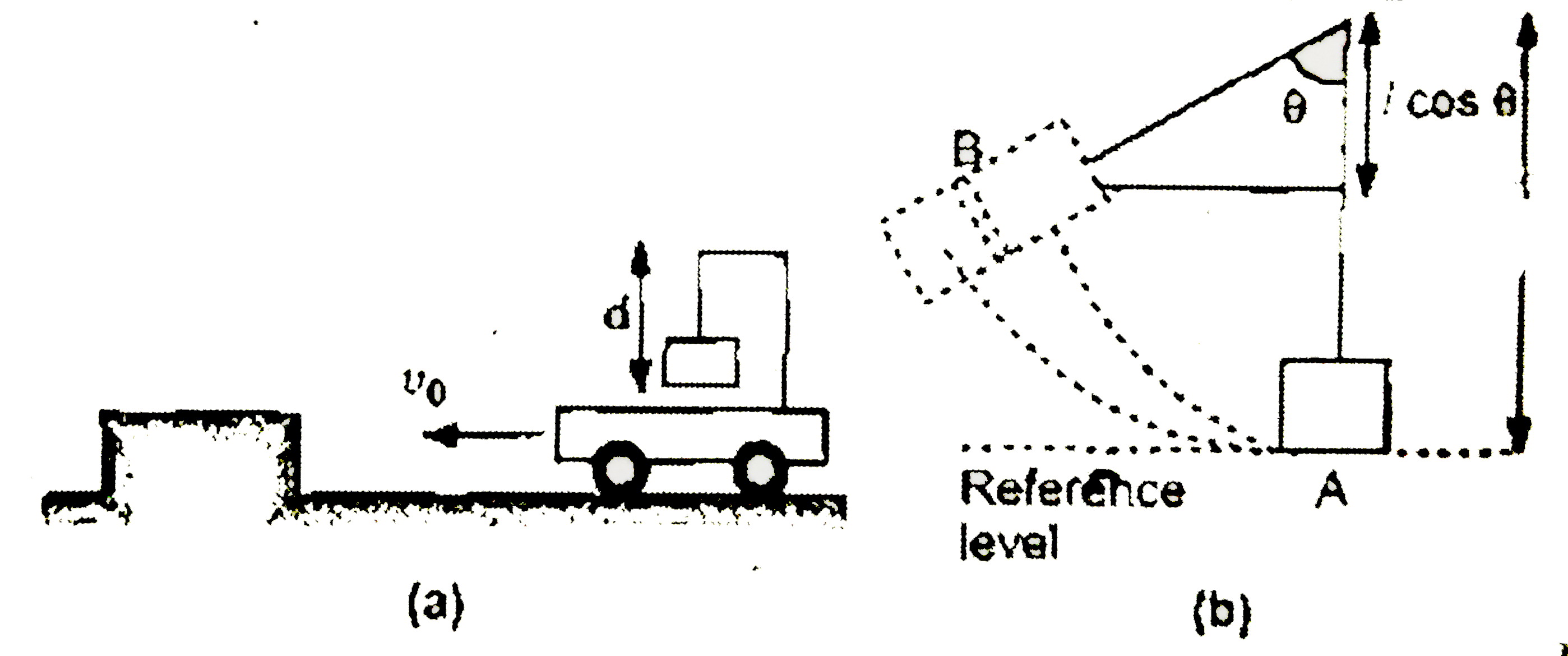
View SolutionA pendulum bob is suspended on a flat car that moves with velocity `v_(0)`. The flat car is stopped by a bumper:
(a) What is the angle through which the pendulum swings.
(b) If the swing angle is `theta = 60^(@)` and `1 = 5m`, what was the initialy speed of the flat car ?
View SolutionA pendulum bob can swing along a ciircular path on a smooth inclined plane, as shown in Fig. 3E.31, where `m = 1.2 kg, 1 = .075m, theta = 37^(@)`. At the lowest point of the circle the tension in the sting is `T = 110 N`. Determine
(a) the speed of the bob at the lowest point,
(b) the speed of the bob at the highest point on the circle and
(c) the tension in the string at the highest position
(a)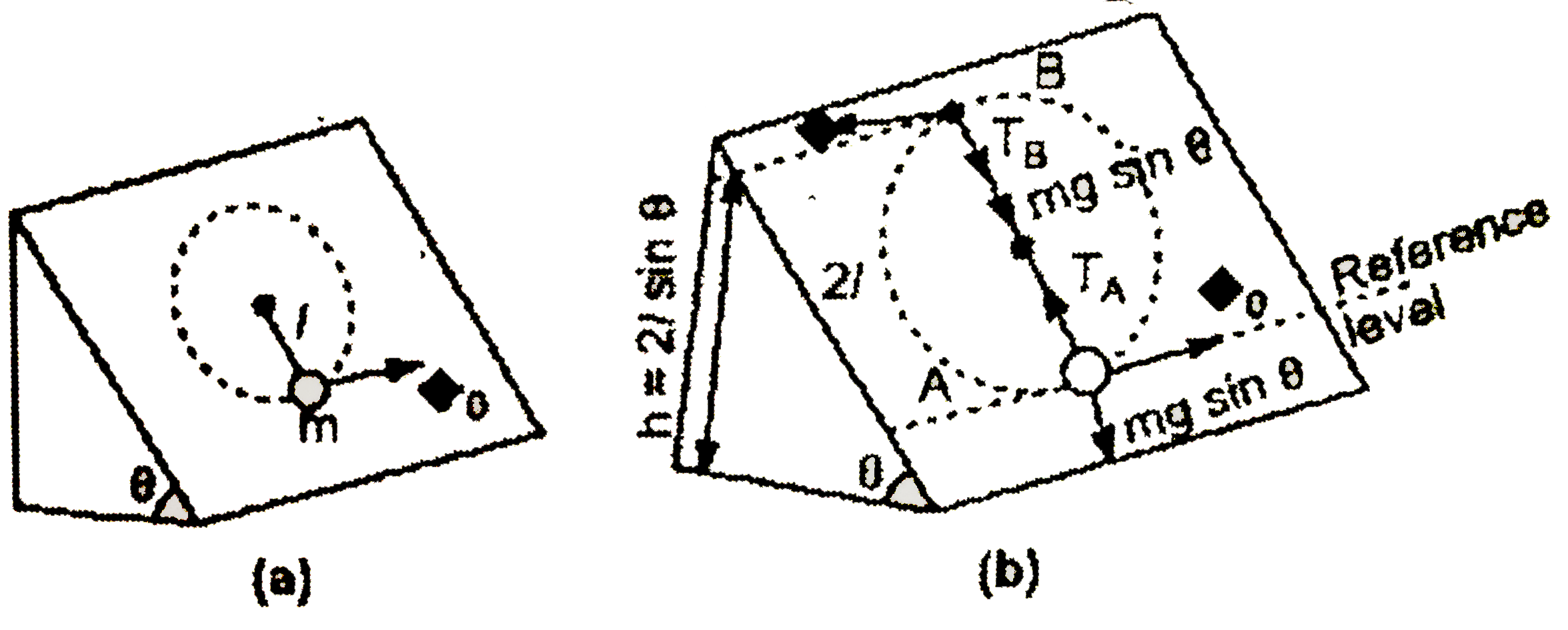
View SolutionA small toy car of mass m slides with negligible friction on a ''loop'' the loop track as shown in Fig.3E.32. The toy car starts from rest at a point H above the level of the lowest point of the track
(a) If `H = 2R`, what normal force is exerted by the track on the toy car at point q?. What are the speed and normal force at point r ?
(b) At what height will the ball leave the track and to what maxiumum height will it rise afterwards ?
(c) If `H = 4R`, what is the speed and normal reaction reaction at point s ?

View SolutionA small ball is rolled with speed u from point A along a smooth circular track as shown in Fig. 3E.33. If `x = 3R`, determine the required speed u so that the ball returns to A, the point of projection. What is the minimum value of x for which the ball can reach the point of projection ?

View SolutionA block of mass m is pressed against a spring of force constant k. The block after leaving contact with the spring moves along a ''loop'' the loop track. The sliding surface is smooth except for rough portion of length s equal to R as shown in Fig. 3E.34, where the coefficient of friction is `mu_(k)`. Determine the minimum spring compression x for which the particle will not lose contant with the track ?

View SolutionA particle attached to a vertical string of length 1m is projected horizontally with a velocity `5 sqrt2 m//s`
(a) What is maximum height reached by the particle from the lower most point of its trajectory.
(b) If the string breaks when it makes an angle of `60^(@)` with downward vertical, find maximum height reached by the particle from the lower most point of its trajectory
View SolutionA particle is suspended by a light vertical inelastic string of length 1 from a fixed support. At its equilbrium position it is projected horizontally with a speed `sqrt(6 g l)`. Find the ratio of the tension in the string in its horizontal position to that in the string when the particle is vertically above the point of support.
View SolutionA small ball is hung as shown an a string of length L.
(a) If `v_(0) gt sqrt(6 g l)`, find the angle `theta ( lt 90^(@))` [in terms of, `v_(0), g, L`] with the upward vertical at which the string becomes slack.
(b) find the value of `v_(0)` [ in terms of g, L] if the particle passes through point of suspension

View SolutionA simple pendulum swings with angular amplitude `theta`. The tension in the string when it is vertical is twice the tension in its extreme position. Then, ` cos theta` is equal to
View SolutionA heavy particle hanging from a string of length l is projected horizontally with speed `sqrtgl`. Find the speed of the particle at the point where the tension in the string equals weight of the particle.
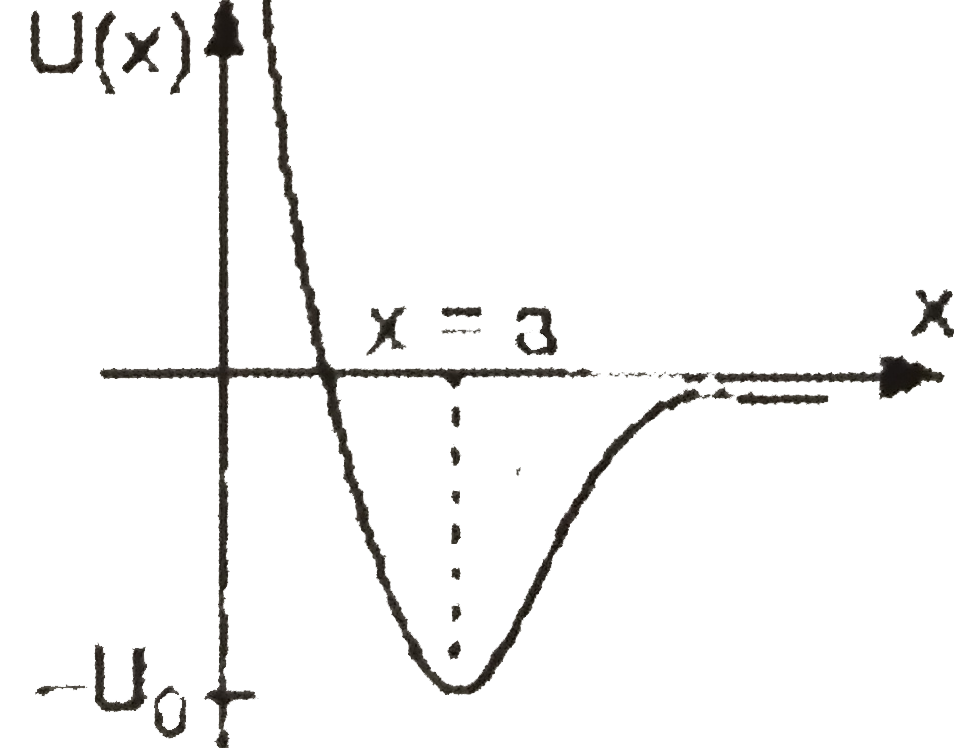
View SolutionThe force between two atoms in a diatomic molecule can be represented approaximately by the potential energy function
`U = U_(0) [((a)/(x))^(12) - 2 ((a)/(x))^(6) ]`
where `U_(0)` and a are constant (a) At what value of x is the potential energy zero ?
(b) Fidn teh force `F_(x)`. (c) At what value of X is the potential energy a minmum ?
View SolutionA body of mass `2 kg` is moving under the influence of a central force whose potential energy is given by `U = 2r^(3) J`. If the body is moving in a circular orbit of `5 m`, its energy will be
View SolutionA single conservative force `F(x)` acts on a `1.0-kg` particle that moves along the x-axis. The potential energy `U(x)` is given by `U(x)=20+(x-2)^2` where x is in meters. At `x=5.0m`, the particle has a kinetic energy of `20J`.
Determine the equation of `F(x)` as a function of x.
View SolutionConsider a one-dimensional motion of a particle with total energy E. There are four regions A, B, C and D is which the relation between potential energy U, kinetic energy (K) and total energy E is as given below
RegionA:`UgtE` Region B:`UltE`
Region C:`KltE` Region D:`UgtE`
State with reason in each case whether a particle can be found in the given region or not.
View SolutionTwo particle of mass m and 2m, connected by a massless rod, slide on the insider of a smooth circular ring of radius r, as shown in Fig. 3E.44 (a). If the assembly is released from rest when `theta = 0`, determine
(a) the velocity of the particle when the rod passes the horizontal position,
(b) the maximum velocity `v_("max")` of the particles.

View SolutionThe figure shows a pendulum of length l suspended at a distance x vertically above a peg.
(a) The pendulum bob is deflected through an angle `theta` and then released. Find the speed of the bob at the instant
(b) The pendulum is released when `theta = 90^(@)`. For what x (position of peg) will the pendulum complete the circle ?
(c) The pendulum is released when `theta = 60^(@)`. what is the velocity of the bob as it passes position E.

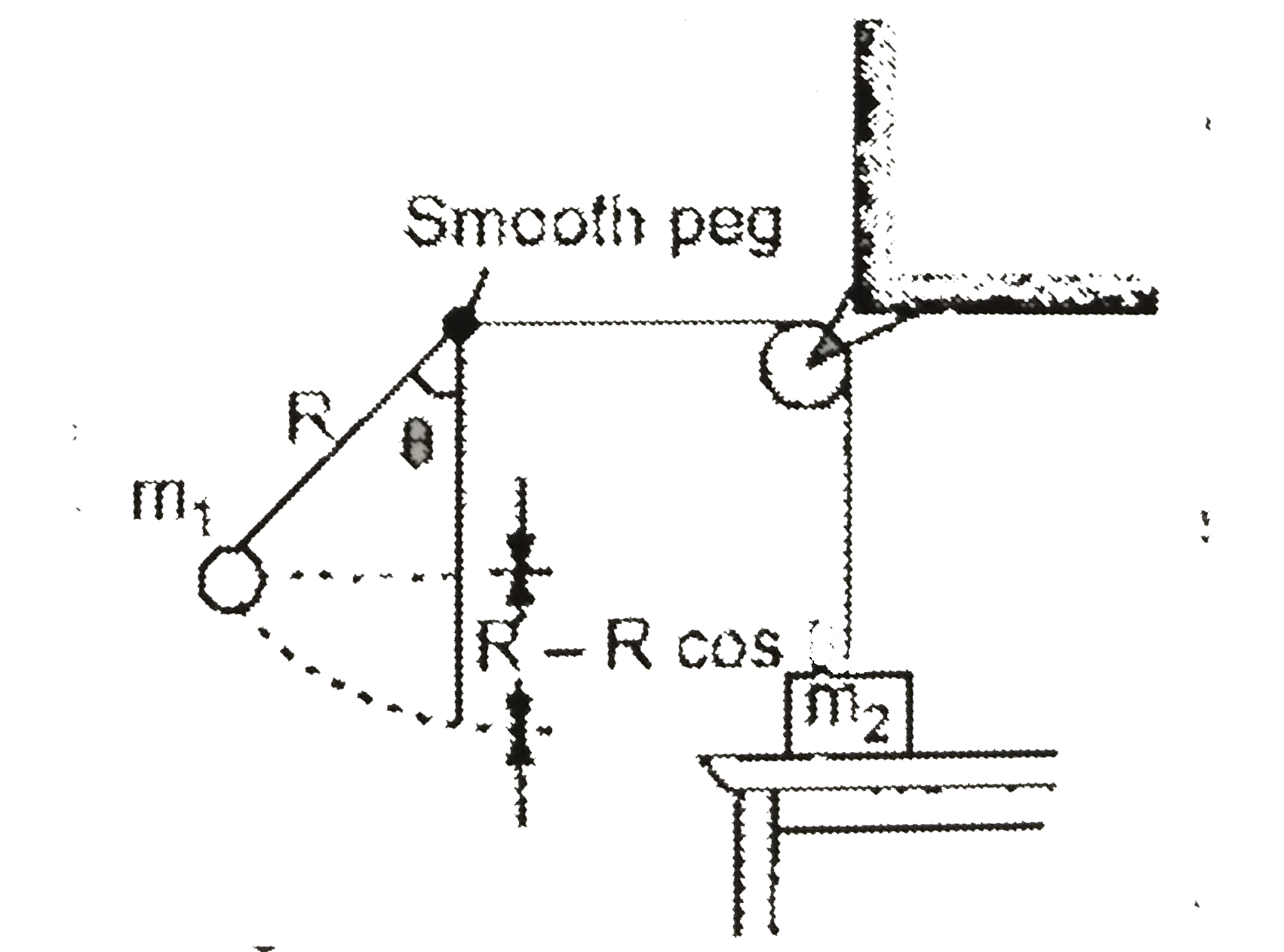
View SolutionTwo blocks are connected by a massless string that passes over a frictionless peg as shown in Fig. 3E.46. One end of the string is attached to a mass `m_(1) = 3 kg` i.e. a distance `R = 1.20 m` from the peg. The other end of the string is connected to a block of mass `m_(2) = 6 kg` resting on a table. From what angle `theta`, measured from the vertical, must the 3 kg block be released in order to just lift the 6 kg block off the table ?
View SolutionFig. 3E.47 (a) shows a circular ring of mass M that hangs in a vertical plane. Two beads of mass m are released simultaneously from the top of the ring in opposite directions. There is no frictional force between the bead and the ring. Show that the ring will starts to rise if `m gt (3M)/(2)`. If m = 2M, at what angle `theta` from vertical this happends ?
(a)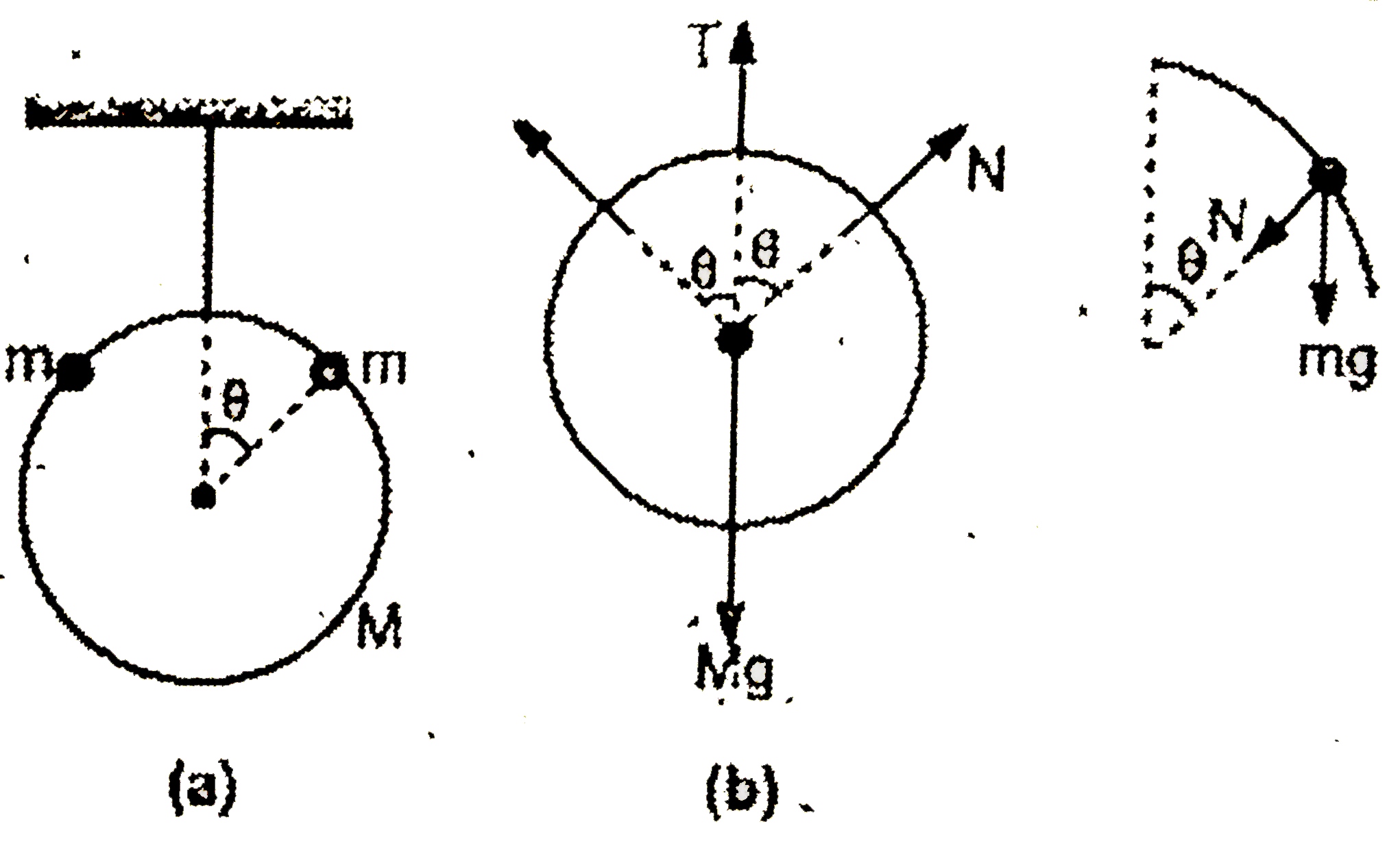
View SolutionA force acting on a certain particle depends of the particles position in the xy-plane. This force F is given by the expression
`vec(F) = (xy hat(i) + xy hat(j)) (1 N//m^(2))`
where x and y are expressed in metre. If `vec(F)` is a conservation force ?
View Solution
Eample questions and complete solutions for chapter WORK AND ENERGY of SHREE BALAJI PHYSICS (HINGLISH) of Class 11