Complete Solutions to Level 1 of chapter WORK AND ENERGY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK AND ENERGY |
| ANURAG MISHRA | Level 1 |
| Number Of Questions | 53 |
| Academic Year | 2023-24 |
A small block of mass m is kept on a rough inclined surface of inclination `theta` fixed in an elevator. The elevator goes up with a uniform velocity v and te block does not slide n te wedge. The work done by the force of friction on the block in time t will be
View SolutionConsider two observers moving with respect to each other at a speed v along·a straight line. They observe a block of mass m moving a distance 1 on a rough surface. The following quantities will be same as observed by the observers
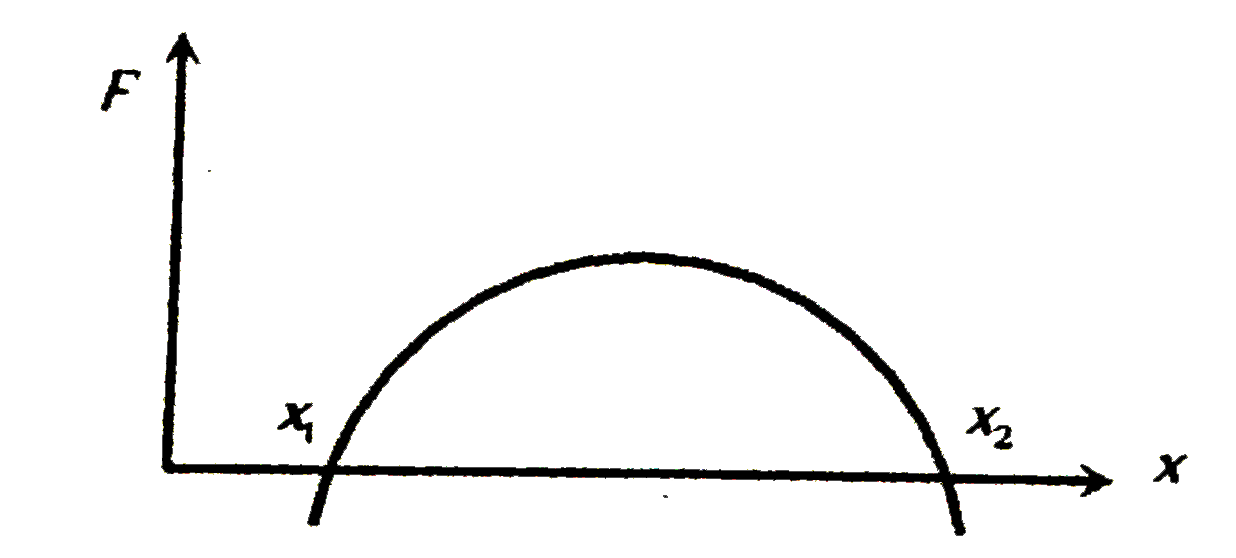
View SolutionThe force acting on a body moving along x -axis varies with the position of the particle as shown in the fig. The body is in stable equilibrium at.
View SolutionA uniform chain has mass Mand length L. It is lying on a smooth horizontal table with half of its length hanging vertically downward. The work done in pulling the chain up the table is:
View SolutionA block is resting over a smooth horizontal plane. A constant horizontal force starts acting on it at `t = 0`. Which of the following graph is correct:
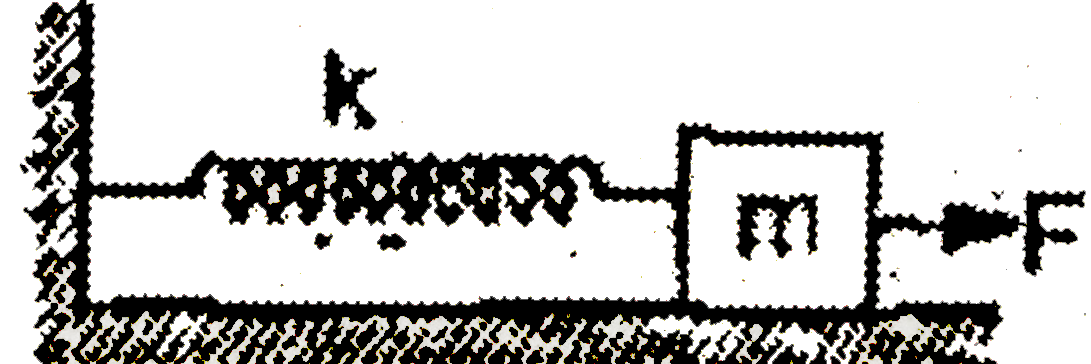
View SolutionIf the block in the shown arrangement is acted upon by a· constant force F for `t le 0`, its maximum speed will be:
View SolutionA block hangs freely from the end of a spring. A boy then slowly pushes the block upwards so that the spring becomes strain free. The gain in gravitational potential energy of the block during this process is not equal to
View SolutionA particle of mass m is moving in a circular path of constant radius r such that its centripetal acceleration `a_(c)` is varying with time t as `a_(c) = k^(2)rt^(2)`, where k is a constant. The power delivered to the particle by the forces acting on it is :
View SolutionA self-propelled vehicle of mass m, whose engine delivers a constant power P, has an acceleration `a = (P//mv)`. (Assume that there is no friction). In order to increase its velocity from `v_(1)` to `v_(2)`, the distan~e it has to travel will be:
View SolutionA stone tied to a string of length `L` is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time the stone is at lowest position and has a speed `u` . Find the magnitude of the change in its velocity as it reaches a position, where the string is horizontal.
View SolutionA ball of mass 5.0 gm and relative density 0.5 strikes the surface of the water with a velocity of 20 m/sec. It comes to rest at a depth of 2m. Find the work done by the resisting force in water: (take `g = 10 m//s^(2)`)
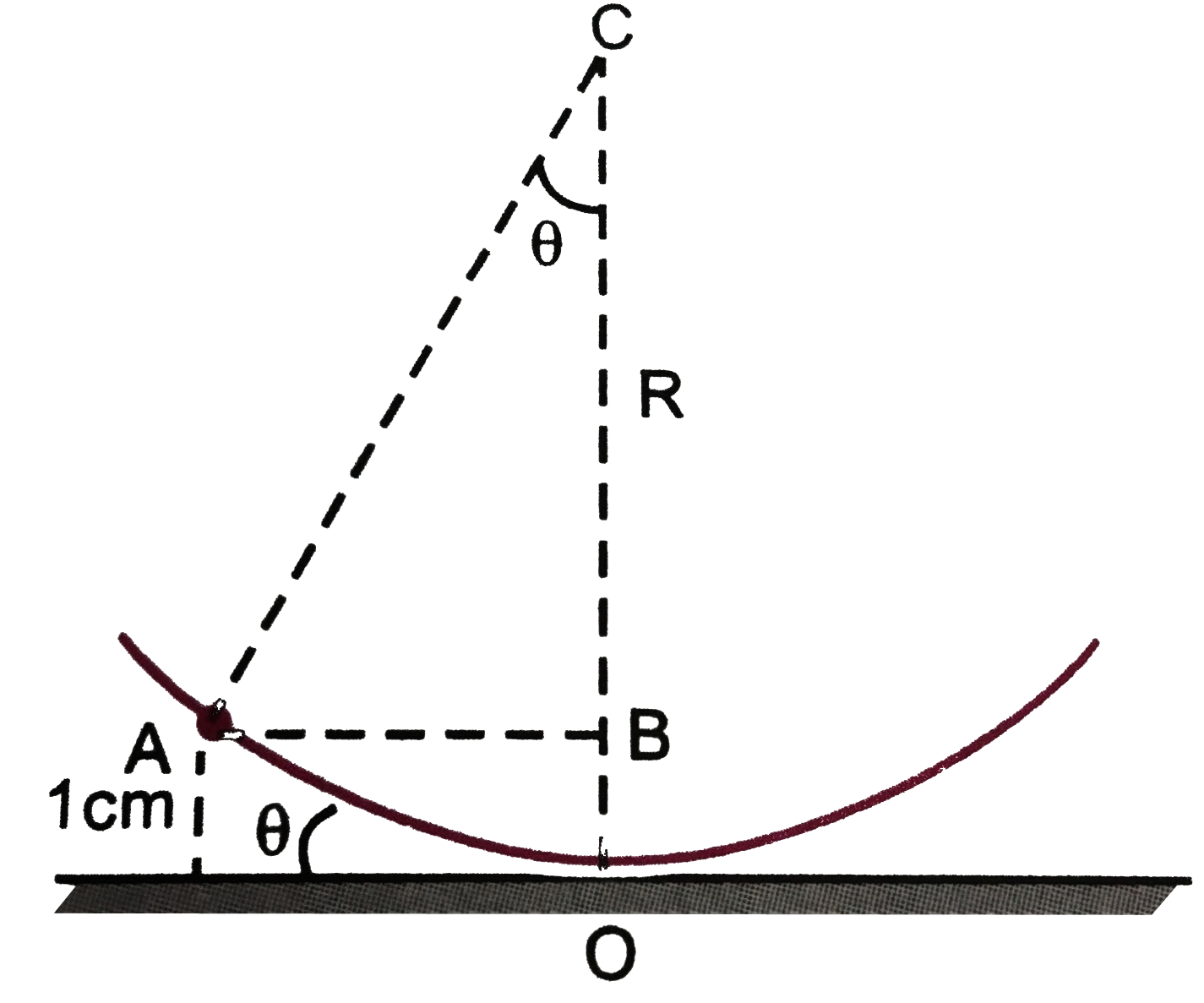
View SolutionAparticle of mass 1 g executes an oscillatory motion on the concave surface of a spherical dish of radius 2m placed on a horizontal plane, Figure . If the motion of the particle begins from a point on the dis at a height of 1 cm. from the horizontal plane and coefficient of friction is 0.01 , fing the total distance covered by the particle before coming to rest.
View SolutionA spring is compressed between two toy carts to masses `m_1` and `m_2`. When the toy carts are released, the spring exerts on each toy cart equal and opposite forces for the same small time t. If the coefficients of friction `mu` between the ground and the toy carts are equal, then the magnitude of displacements of the toy carts are in the ratio
View SolutionA light spring is hung vertically from a fixed support and a heavy mass is attached to its. lower end. The mass is then slowly lowered to its equilibrium position: This stretches the spring by an amount d. If the same body is permitted to fall instead, through what distance does it stretch the string?
View SolutionA running man has half the KE that a body of half his mass has. The man speeds up by `1.0ms^(-1)` and then has the same energy as the boy. What were the original speeds of the man and the boy?
View SolutionAn elastic spring of unstretched length `L` and force constant `K` is stretched by amoun t `x` .It is further stretched by another length `y` The work done in the second streaching is
View SolutionA ball P is projected vertically up. Another similar ball Q is projected at ari angle `45^(@)`. Both reach the same height during their motion. Then, at the starting point, ratio of kinetic energy of P and Q is?
View SolutionA particle of mass m is moving in a horizontal circle of radius r, under a centripetal force equal to `(-K//r^(2))`, where k is a constant. The total energy of the particle is -
View SolutionA `10 kg` block is pulled along a frictionless surface in the form of an arc of a circle of radius `10 m`. The applied force is `200 N`. Find the work done by (a) applied force and (b) gravitational force in displacing through an angle `60^@`.
 .
.
View Solution1 kg block collides with a horizontal massless spring of force constant `2 N//m`. The block compresses the spring by 4m. If the coefficient of kinetic friction between the block and the· surface is 0.25, what was the speed of the block at the instant of collision? (take `g = 10 m//s^(2)`)

View SolutionA stone with weight W is thrown vertically upward into the air with initial velocity `v_(0)`. If a constant forcef due to air drag acts on the stone throughout the flight & if the maximum height attain by stone is h and velocity when it strikes to the ground is v. Which one is correct?
View SolutionA stone of mass m, tied to the end of a string, is. whirled around in a horizontal circle (neglect gravity). The length of the string is reduced gradually such that mvr = constant. Then, the tension in the string is given · by `T = Ar`'', where A is a constant and r is the instantaneous radius of the circle. Then, n is equal to:
View SolutionA block of mass m released from rest from point O as shown below. The velocity of the block at the lowest points are v O , v E, v F respectively. Assume coefficient of kinetic friction between surface and the block is same in all cases. Then,
(a)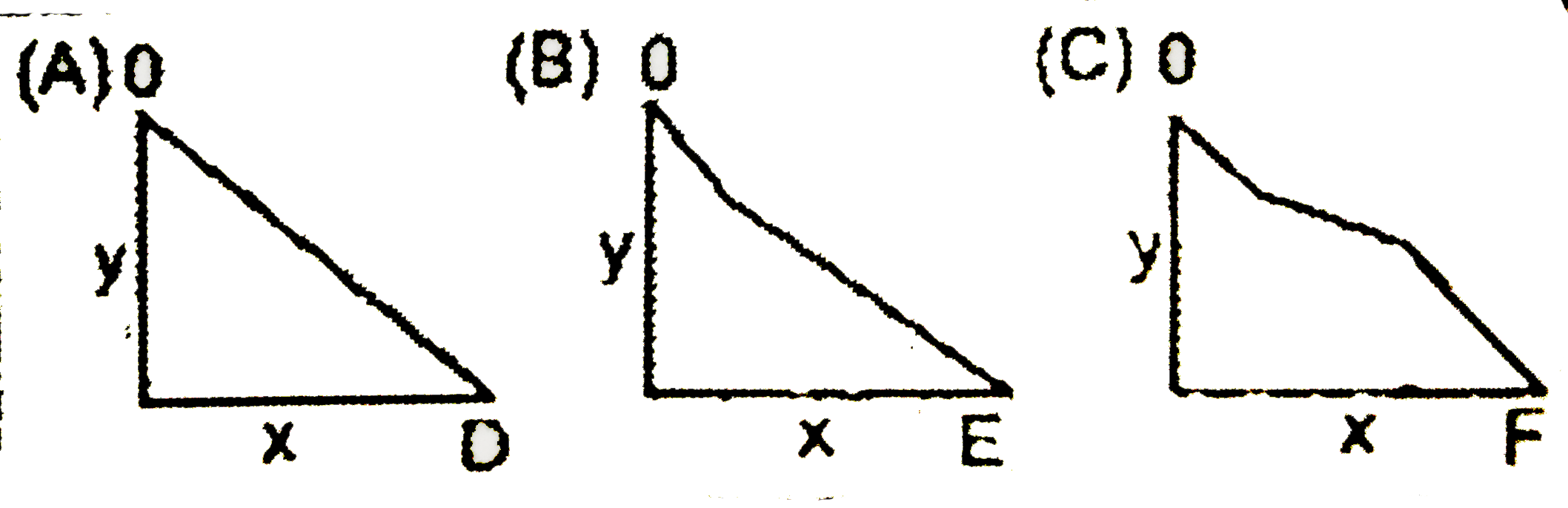
View SolutionThe mass m slides down the track and completes the vertical circle on the smooth curved surface. The minimum value of h will be:

View SolutionA body of mass m is moving in a circle of radius 'r' with a constant speed v. The force on the body is `(mv^(2))/(r)` and is r directed towards the center. If work done by this force in moving the body over half the circumference and complete circumference is W and W', then:
View SolutionIn the shown figure, a small mass m starts sliding down a smooth and stationary circular track. Which of the following graph best represents the variation of magnitude of the force applied by the track on the mass and the angle `theta`?
View SolutionIn the Q. No. 26, if `M = 2 m` and friction exists between the circular track and the horizontal surface then, which of the following lot best represents the variation of frictional force versus the angle `theta`:
View SolutionA particle of mass m is whirled in a vertical circle with the help of a thread. `If^(-)` the maximum tension in the thread is double its minimum value then the value of minimum tension in the thread will be:
View SolutionA particle of mass m is located in a one dimensional potential field where potential energy of the particle has the form `U (x) = (a)/(x^(2)) - (b)/(x)` where a and b are positive constants. The position of equilibrium is:
View SolutionTwo cylindrical vessels of equal cross-sectional area. A contain water upto height `h_(1)` and `h_(2)`. The vessels are interconnected so that the levels in them becomes equal. The work done by the force of gravity during the process is:
View SolutionA block of mass 100 g moved with,a speed of 5 m/s at the highest point in a closed circular tube of radius 10 ,cm kept in a vertical plane. The cross-section of the tube is such that the block just fits in it., The block makes several oscillations inside the tube and finally steps at the lowest point. The work done by t\Ie tube on the block during the process is:
View SolutionA heavy stone is thrown from a cliff of height h with a speed .v. The stone will hit ground with maximum speed if it is thrown:
View SolutionTwo springs A and B `(k_(A) = 2k_(B))` are stretched by applying forces of equal magnitudes at the four ends. If the energy stored in A is E, that in B is:
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out ,YI)l~etri~ally to ~tretch the spring by a length· x over its natural length. The work done by the spring on each mass is:
View SolutionThe negative of the work done 'by the conservative internal forces on a system equals the change in:
View SolutionThe work done by the external forces on a system equals the change in
View SolutionThe work done by all the forces (external and internal) on a system equals the change in
View Solution__________ of a two particle system depends only on the separation between the two particles. The most appropriate choice for the blank space n the above sentence is
View SolutionA block of mass m slides down a smooth vertical circular track. During the motion, the block is in:
View SolutionA particle is rotated in a vertical circle by connecting it to a string of length `l` and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
View SolutionIn the shown diagram mass of A is m and that of B is 2 m. All the surfaces are smooth. System is released from rest with spring unstretched. Then, the maximum extension `(x_(m))` in spring will be:

View SolutionIn above question, speed of block A, when the extension in spring is `(x_(m))/(2)`, is:
View SolutionA chain of length L and mass Mis arranged as shown in following four cases. The correct decreasing order of potential energy (assumed zero at horizontal surface) is:
(i)
View SolutionA block of mass m is pulled by a constant powert `P` placed on a rough horizontal plane. The friction coefficient the block and surface is `mu`. The maximum velocity of the block is.
View SolutionForces acting on a particle moving in a straight line varies with the velocity of the particle as `F = (alpha)/(upsilon)` where `alpha` is constant. The work done by this force in time interval `Delta t` is :
View SolutionA pendulum of mass 1 kg and length = 1m is released from rest at angle = 60º. The power delivered by all the forces acting on the bob at angle = 30º will be: (g = 10 m/s2)
View SolutionA system consists of two identical cubes, each of mass m, linked together by the compressed weightless spring of stiffness `ϰ` (figure). The cubes are also connected by a thread which is burned through at a certain moment. Find:
(a) at what values of `Deltal`, the initial compression of the spring, the lower cube will bounce up after the thread has been burned through:
(b) to what height h the centre of gravity of this system will rise if the initial compression of the spring `Deltal=7mg//ϰ`.
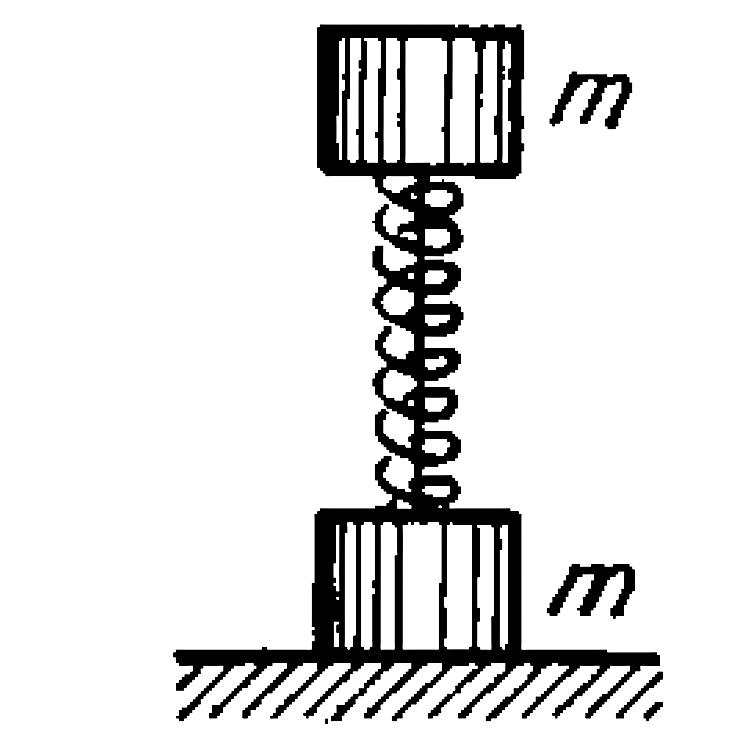
View SolutionIn the shown figure, the mass in sticks to the string just after it strikes it. Then the minimum value of h, so that the lower mass bounce off the ground during 'its rebound is:
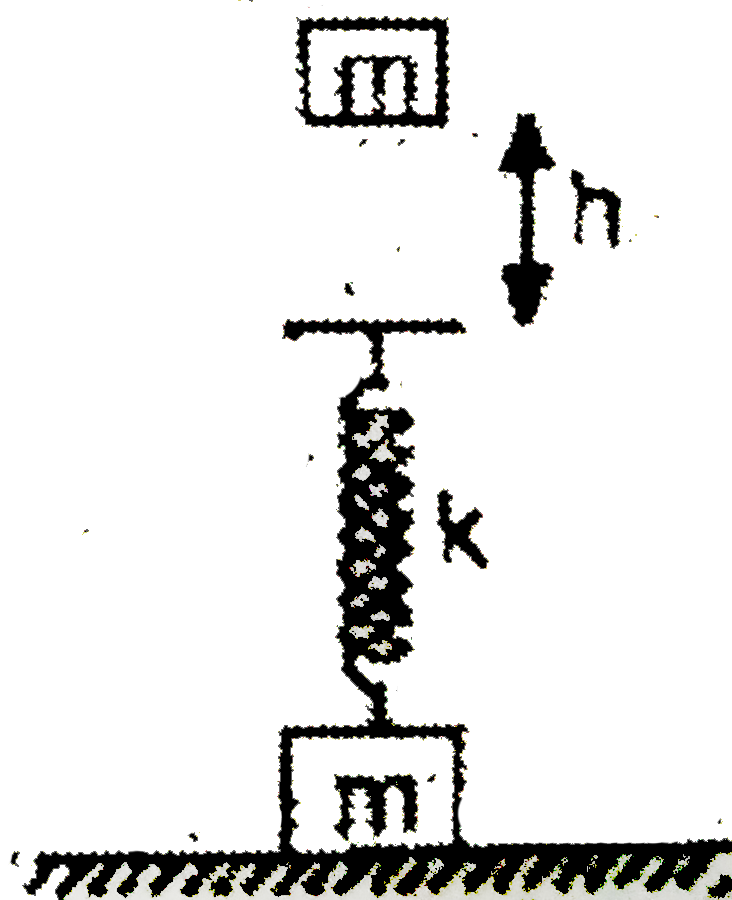
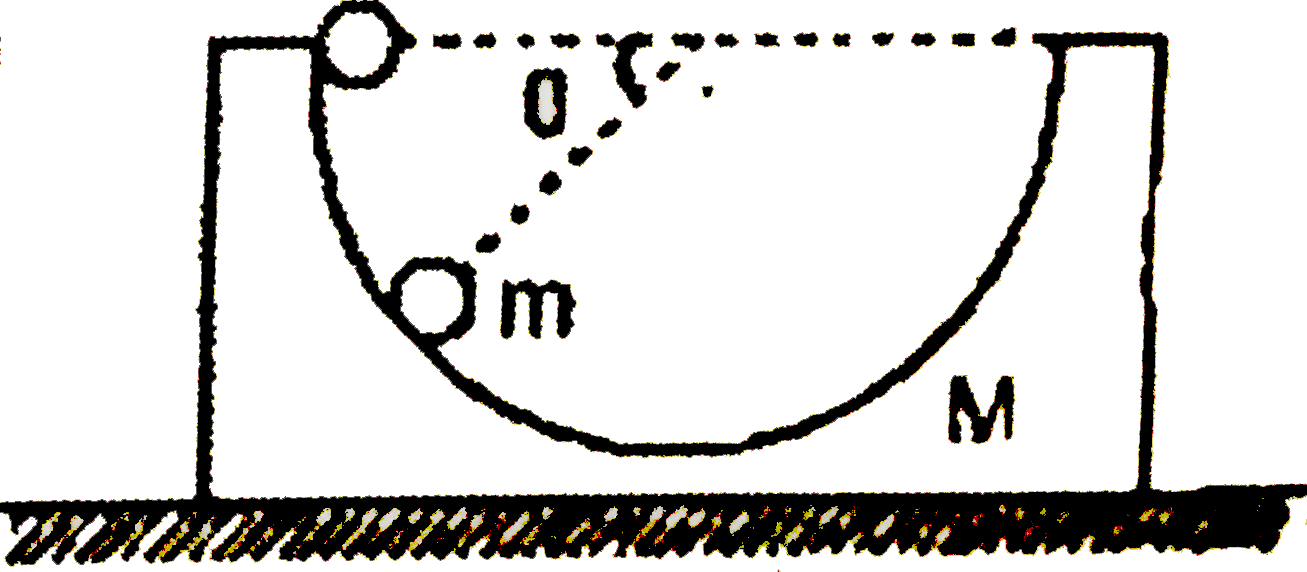
View SolutionA circular tube of mass `M` placed veticlly on a horizontal surface as shown in the figure. Two small spheres, each of mass `m` , just fit in the tube, are released from the top. If `theta` gives the angle between radius vector of eirther ball with the vertical, obtain the value of the ratio `M//m` if the tube breacks its contact with ground when `theta=60^(@)` . Neglect any friction.

View SolutionA spring mass system is held at rest with the spring relaxed at a height `(H)` above the ground. Determine the minimum value of `(H)` so that the system has a tendency to rebound after hitting the ground. Given that the coefficient of restitution between `(m_(2))` and ground is zero.
 .
.
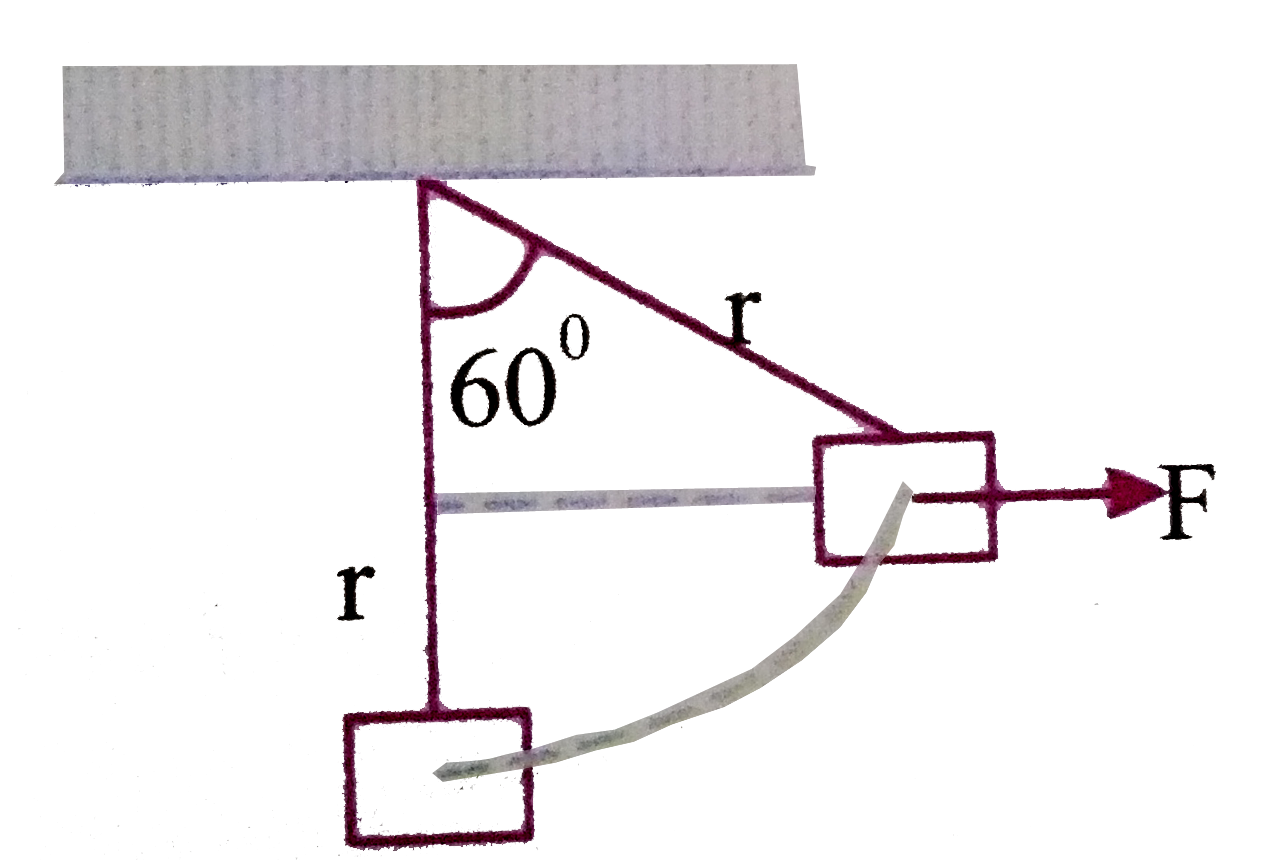
View SolutionIn shown figure, the trolley starts accelerating with acceleration a. The maximum angle deflected by thread from vertical will be:
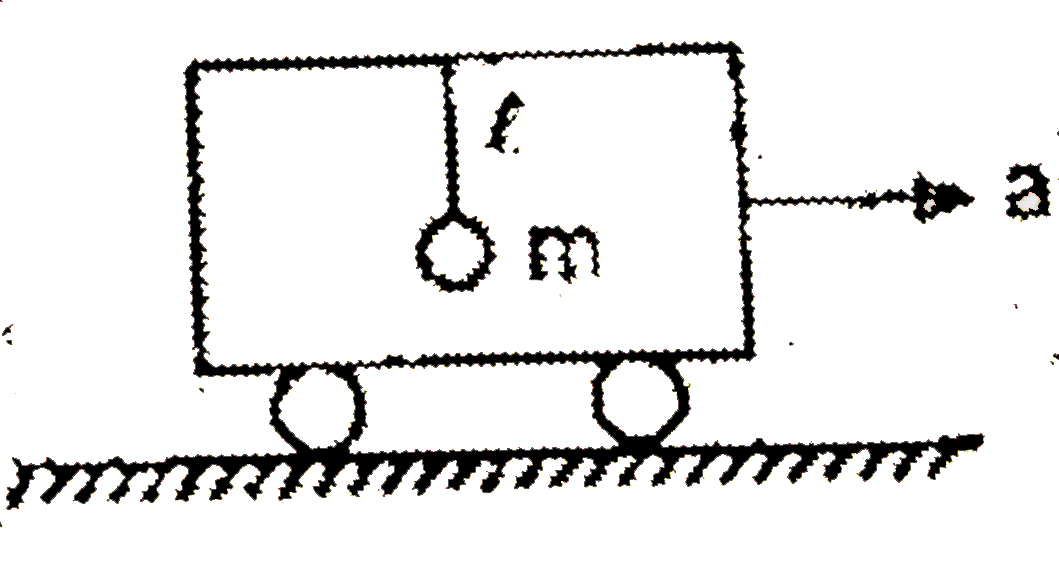
View SolutionA force `F=-K(yhati+xhatj)` (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point `(a, 0)`, and then parallel to the y-axis to the point `(a, a)`. The total work done by the force F on the particle is
View SolutionA particle free to move along the (x - axis) hsd potential energy given by `U(x)= k[1 - exp(-x^2)] for -o o le x le + o o`, where (k) is a positive constant of appropriate dimensions. Then.
View Solution
Level 1 questions and complete solutions for chapter WORK AND ENERGY of SHREE BALAJI PHYSICS (HINGLISH) of Class 11