Complete Solutions to Illustation of chapter IMPULSE AND MOMENTUM of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | IMPULSE AND MOMENTUM |
| ANURAG MISHRA | Illustation |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
Consider ·an astronaut trapped in space, isolated from surrounding. He can reach his spacecraft if some velocity is gained by him somehow. Suddenly he realises that he has got a small pencil in his pocket. How can he acquire velocity (momentum) ?
We take the system to consist of the astronaut and the pencil as shown in Fig. 4.4. We assign the positive direction of the x-axis to be the direction of throw. The gravitational force acts on the $Y5tem, which indeed is external force. However, this force is directed along the y-axis, it will not change momentum along x-axis. we· can thus apply the conservation of momentum to this system. What happens to the force exerted by the astronaut on the pencil while throwing it?
`m_(a) vecV_(ai) + m_(p)vecV _("pi") = m_(a) vecV _(af) + m_(p)vecV _(pf)
0 + 0 = M_(a)vecV_(af) + m_(p)vecV _(pf)
vecV_(af) =-(m_(P)vec_(pf))/m_(a)`
The negative sign indicates that the astronaut moves in the direction opposite. to the direction of motion of the pencil.

View SolutionA block speed of mass `m` and a pan of equal mass are connected by a string going over a smooth light pulley. Initially, the system is at rest, then a particle of mass `m` falls on the pan ad sticks to it. If the particle strikes the pan with a speed `v`, find the speed with which the system moves just after the collision.
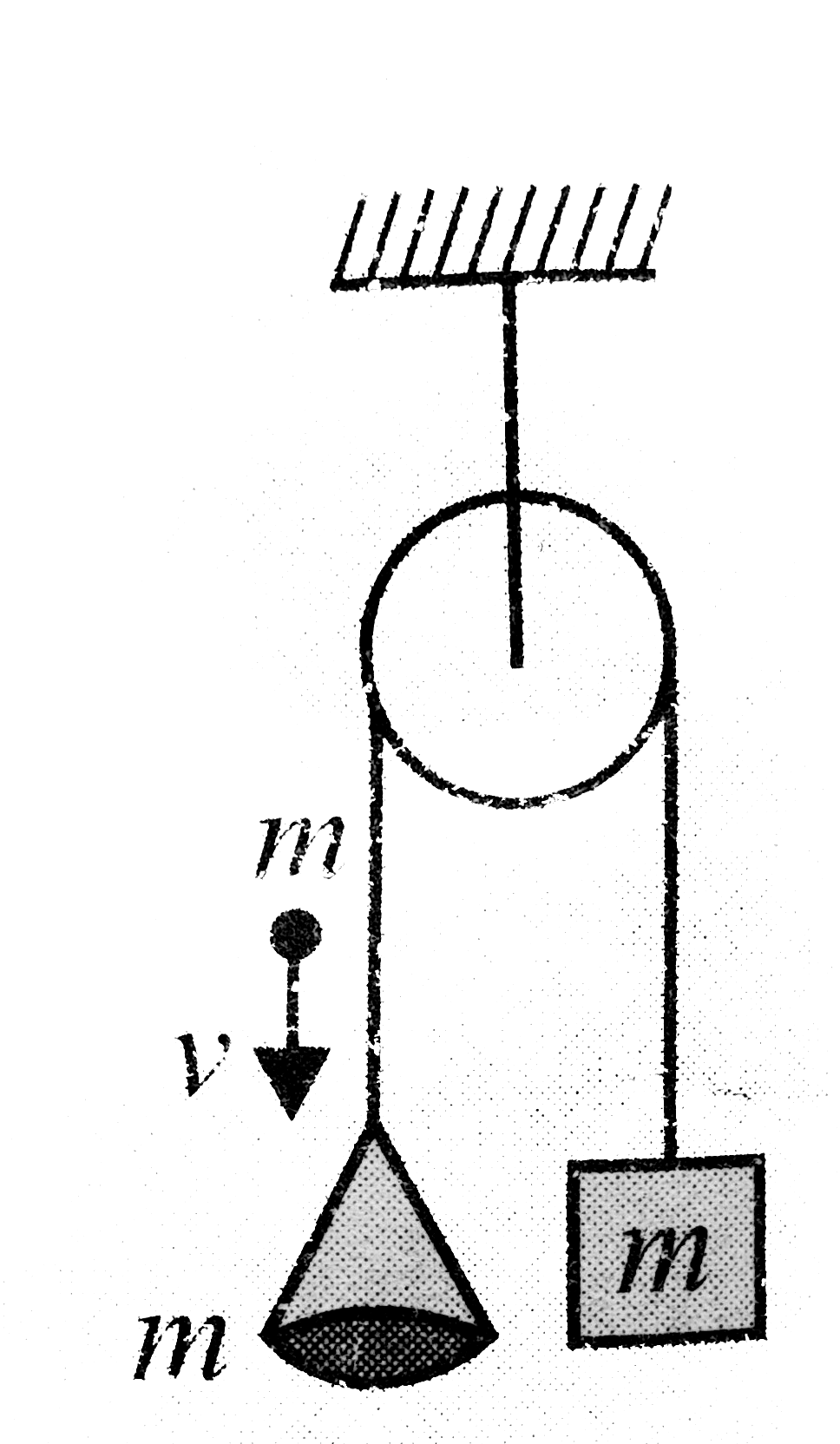
View SolutionTwo identical blocks `A` and `B` connected by massless string, are placed on a frictionless horizontal plane. A bullet havig the same mass, moving with speed `u` strickes block `B` from behind as shown. If the bullet gets embedded into block `B` then find

a. the velocity of `A,B,C` after collision.
b. impulse on `A` due to tension in the string,
c. impulse on `C` due to normal force of collision,
d. impulse on `B` due to normal force of collision.
View SolutionIn the fig 4.24 a block of mass m moves with velocity `v_(0)` toward a stationaly block of a mass M on a smooth horizontal surface. Find the maximum compression in the spring of stiffnesss constant K.

View SolutionIn the fig 4 .25 shown, if all the surfaces are smooth , then determine the maximum height h attained by the block on the wedge, assuming it to be very large .
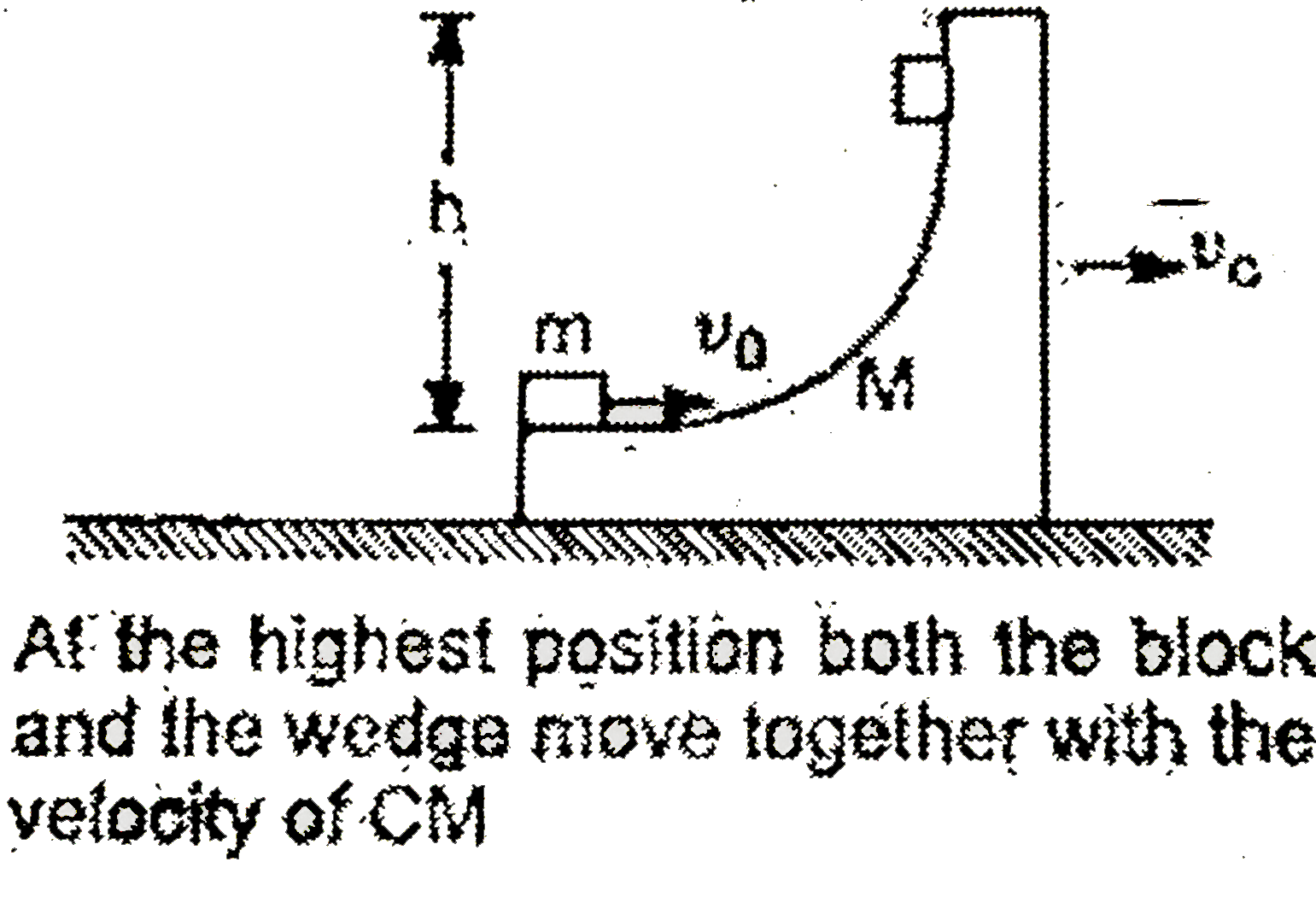
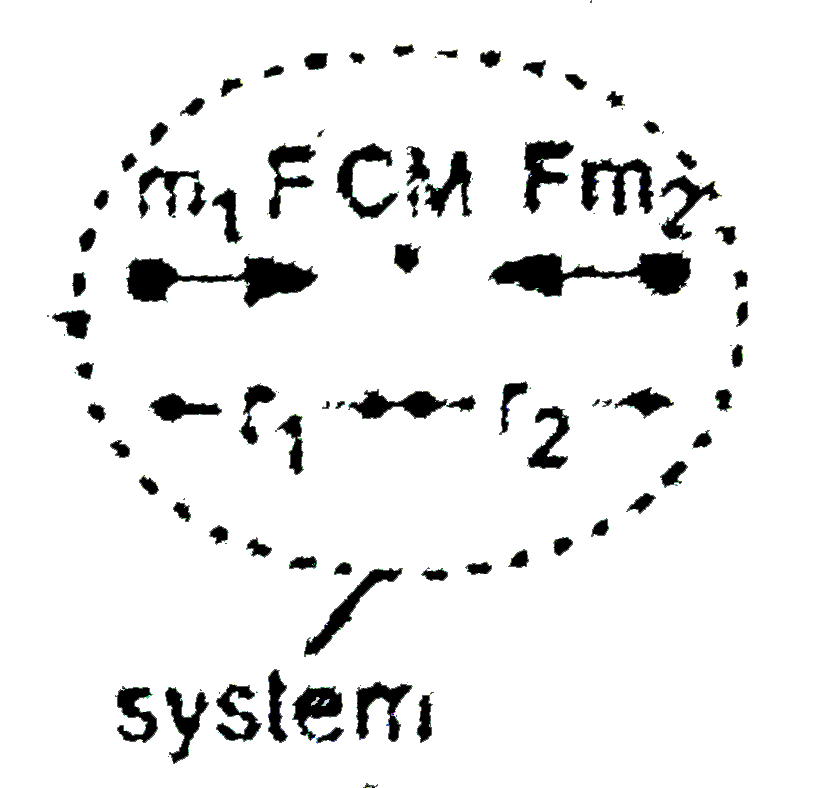
View SolutionConsider a system of two particles of masses `m_(1)` and `m_(2)` separated by a distance r. Suppose they start to move towards each other due to their mutual attraction (attractive force may be electrical, gravitational, etc.).
View SolutionA projectile of mass mis fired with an initial velocity `v_(0)` at an angle 0 to the horizontal. At its highest point, it explodes into two fragments of equal mass. One of the fragments falls vertically with zero initial speed. Since the only external force acting on the system is gravitational, the motion of centre of mass of the_ system (the fragments) follows the same parabolic path as the projectile would have followed if there had been no explosion. Force of explosion is internal, it cannot change the trajectory of the system.

View SolutionA small sphere of radius R is held against the inner surface of larger sphere of radius `6R` (as shown in figure). The masses of large and small spheres are `4M` and M respectivley. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the large spheres, when the smaller sphere reaches the other extreme position.

View SolutionIf some mass of area is removed from a rigid body, then the position of centre of mass of the remaining postion is obtained from the following formulae.
View SolutionFind the position of centre of mass of the uniform lamina shown in figure.
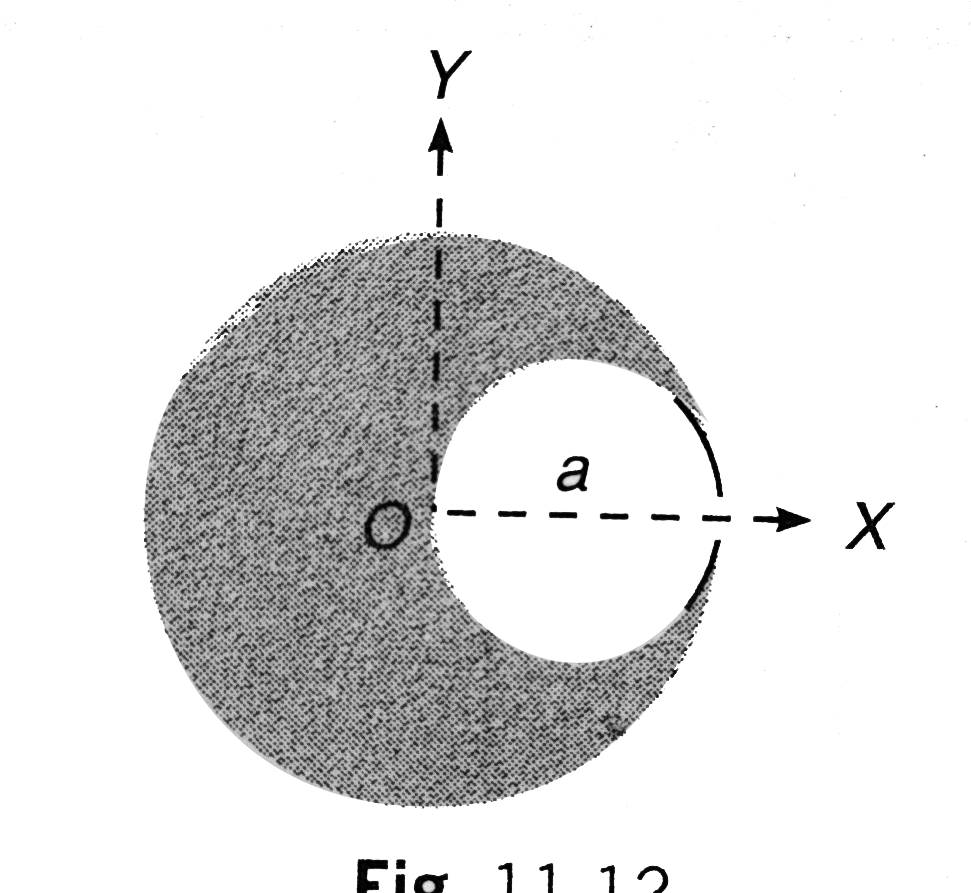
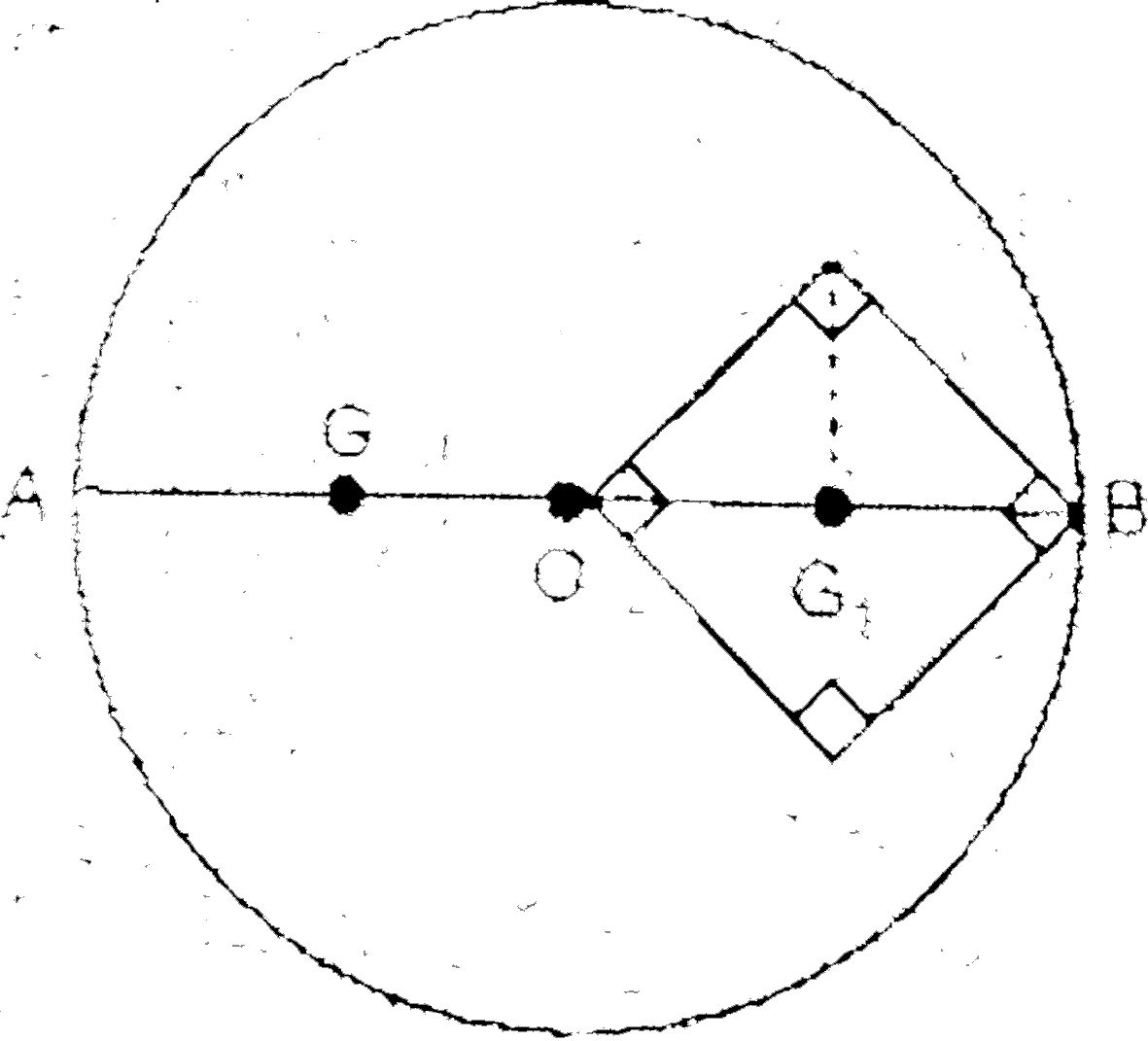
View SolutionA square hole is punched out of a circular lamina, the diagonal of the square being the radius of the circle. If 'a' br the diameter of the circle, find the distance of C.G. of the reamainder form the centre of the circle.
View SolutionThe position vector of three particles of masses `m_1=1kg`.
`m_2=2kg` and `m_3=3kg` are `r_1=(hati+4hatj+hatk)m`, `r_2=(hati+hatj+hatk)m` and `r_3=(2hatj-hatj-2hatk)m` respectivley. Find the position vector of their centre of mass.
View Solutionconsider collision between a block A and a ball B. the block is constrained to move along a horizontal surface. Ignore friction at any of the surfaces. Impulsive. Force between block and ball is along the line of impact and the impulse of reaction exerted by ground is in vertical direction , which is an external force on the system.

View SolutionA ball is moving with velocity `2m//s` towards a heavy wall moving towards the ball with speed `1m//s` as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.

View SolutionA ball of mass `m` moving at speed `v` makes a head on collision with an identical ball at rest. The kinetic energy of the balls after the collision is `3//4th` of the original. Find the coefficient of restitution.
View Solution
Illustation questions and complete solutions for chapter IMPULSE AND MOMENTUM of SHREE BALAJI PHYSICS (HINGLISH) of Class 11