Complete Solutions to Level 1 of chapter IMPULSE AND MOMENTUM of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | IMPULSE AND MOMENTUM |
| ANURAG MISHRA | Level 1 |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A set of n identical cubical blocks lies at rest parallel to each other along a line on a smooth horizontal surface. The separation between the near surfaces of any two adjacent blocks is L . The block at one end is given a speed v towards the next one at time 0 t . All collisions are completely inelastic, then
View SolutionA boy of mass m is standing on a block of mass M kept on a rough surface. When the boy walks from left to right on the block, the centre of mass (boy + block) of the system :
View SolutionA uniform sphere is placed on a smooth horizontal surface and a horizontal force F is applied on it at a distance h above the surface. The acceleration of the centre :
View SolutionAn open water tight railway wagon of mass `5xx10^(3)` kg coasts at initial velocity of `1.2 m//s` without friction on a railway track. Rain falls vertically downwards into the wagon. What change then occurred in the kinetic energy of the wagon, when it has collected `10^(3)` kg of water
View SolutionA body falling vertically downwards under gravity breaks in two parts of unequal masses. The centre of mass of the two parts taken together shifts horizontally towards
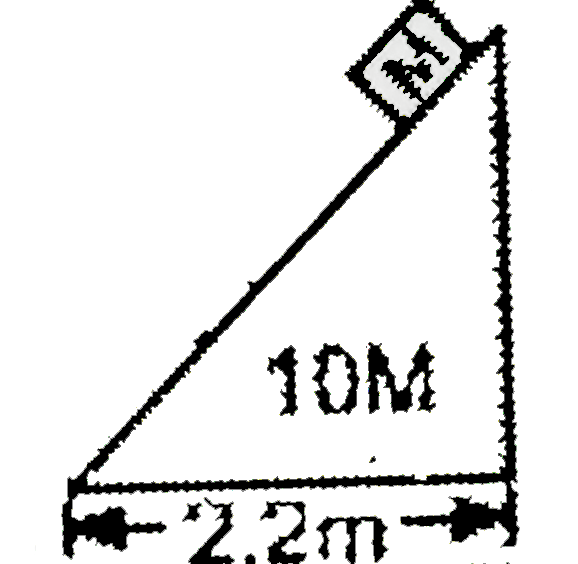
View SolutionA block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
View SolutionIn the figure shown, the two identical balls of mass M and radius R each, are placed in contact with each other on the frictionless horizontal surface. The third ball of mass M and radius `(R )/(2')` is coming down vertically and has a velocity `=upsilon_(0)` when it simultaneously hits the two balls and itself comes to rest. Then, each of the two bigger balls will move after collision with a speed equal to :

View SolutionA ball kept in a closed box moves in the box making collisions with the walls. The box is kept on a smooth surface. The velocity of the centre of mass
View SolutionTwo identical billiard balls are in contact on a table. A third identical ball strikes them symmetrically and comes to rest after impact. The coefficient of restitution is :
View SolutionA ball is projected from ground with a velocity `V` at an angle `theta` to the vertical. On its path it makes an elastic collison with a vertical wall and returns to ground. The total time of flight of the ball is
View SolutionA sphere moving with velocityv strikes elastically with a wall moving towards the sphere with a velocity u. If the mass of the wall is infinitely large, the work done by the wall during collision wiHbe:
View SolutionOn a horizontal smooth surface a disc is placed at rest. Another disc of same mass is coming with impact parameter equal to its own radius. First disc is of radius r. What should be the radius of comping disc so that after collision first disc moves at an angle `45^(@)` to the direction of motion of incoming disc ?
View SolutionA ball is thrown vertically downwards with velocity `sqrt(2gh)` from a height h. After colliding with the ground it just reaches the starting point. Coefficient of restitution is :
View SolutionA ball is projected with initial velocity u at an angle `theta` to the horizontal. Then horizontal displacement covered by ball as it collides third time to the ground would be, if coefficient of restitution is e :

View SolutionA ball is dropped from a height h. As it bounces off the floor, its speed is 80 per cent of what it was just before it hit the floor. The ball will then rise to a height of most nearly:
View SolutionInternal forces can change
View SolutionIn an elastic collision of two billiard balls which of the following quantities is not conserved during the short time of collision :
View SolutionA block of mass M lying on a smooth· horizontal surface is rigidly attached ·to a light horizontal ·spring of spring constant k. The other end of the spring is rigidly connected to a fixed wall. A stationary gun fires ·bullets of mass m each in horizontal direction with speed `upsilon_(0)` one after other. The bullets hit the block and get embedded to it. The first bullet hits the block at t=0, the second bullent hits at `t=2pisqrt((M+m)/(k))+2pisqrt((M+2m)/(k))` and so on. The maximum comression in the spring after the `n^(th)` bullet hits is :
View SolutionA boy hits a baseball with a bat an imparts an impulse `J` to the ball. The boy hits the ball again with the same force, except that the ball and the bat are in contact for twice the amount of time as in the first hit.
View SolutionA shell is fired from a cannon with a velocity `v (m//sec.)` at an angle `theta` with the horizontal direction. At the highest point in its path it explodes into two pieces of equal mass. One of the pieces retraces its path to the cannon and the speed (in `m//sec.`) of the other piece immediately after the explosion is
View SolutionA disc of radis R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
View SolutionThere are some passengers inside a stationary railway compartment. The track is frictionless. The centre of mass of the compartment itself (without the passengers) is `C_(1)`, while the centre of mass of the 'compartment plus passengers' system is `C_(2)`. If the passengers move about inside the compartment along the track.
View SolutionAll the particles of a body situated at distance `d` from the origin. The distance of the center of mass of the body from the origin is
View SolutionTwo trains A and B are running in the same direction on the parallel rails such that A is faster than B. Packets of equal weight are transfcrred from A to B. What will happen due to this :
View SolutionThree blocks are initially placed as shown in the figure. Block `A` has mass `m` and initial velocity `v` to the right. Block `B` with mass `m` and block `C` with mass `4m` are both initially at rest. Neglect friction. All collisions are elastic. The final velocity of blocks `A` is

View SolutionA square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of the plate as shown in figure. Locate the centre of mass of the combination assuming same mass per unit area for the two plates.
View SolutionA rocket of mass 4000 kg is set for vertical firing. How much gas must be ejected per second so that the rocket may have initial upwards acceleration of magnitude `19.6 m//s^(2)` ? [Exhaust speed of fuel`=980 m//s`]
View SolutionSelect the graph (s) which best represent the graph of bouncing ball. Assume ball dropped from height and it losses certain part of energy in each impact,

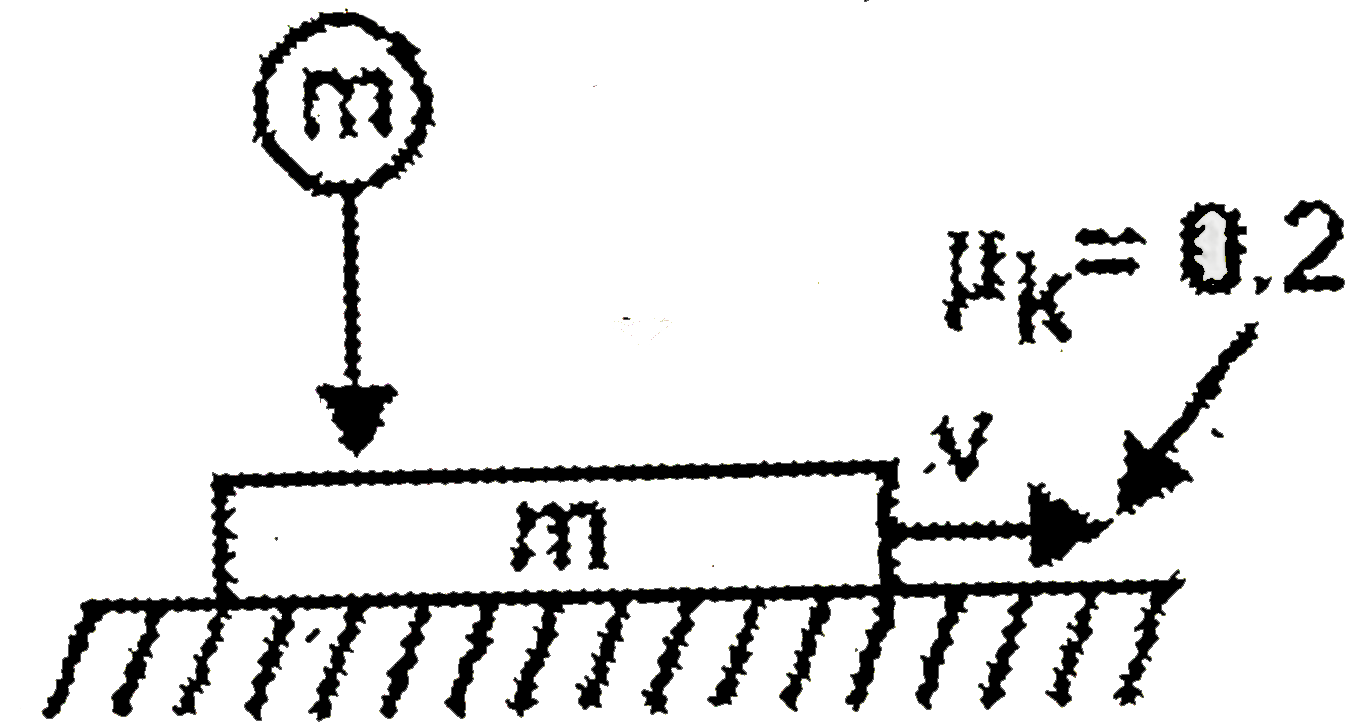
View SolutionA ball of mass m falls vertically from a height h and collides with a block of equal mass m moving horizontally with a velecity `upsilon` on a surface. The coefficient of kinetic friction between the block and the surface is 0.2, while the coefficient of restitution e between the ball and the block is 0.5. There is no friction acting between the ball and the block. The velocity of the blockdecreases by :
View SolutionA particle of mass `m` , initially at rest , is acted upon by a variable force `F` for a brief interval of time `T`. It begins to move with a velocity `u` after the force stops acting . `F` is shown in the graph as a function of time. The curve is a semicircle.

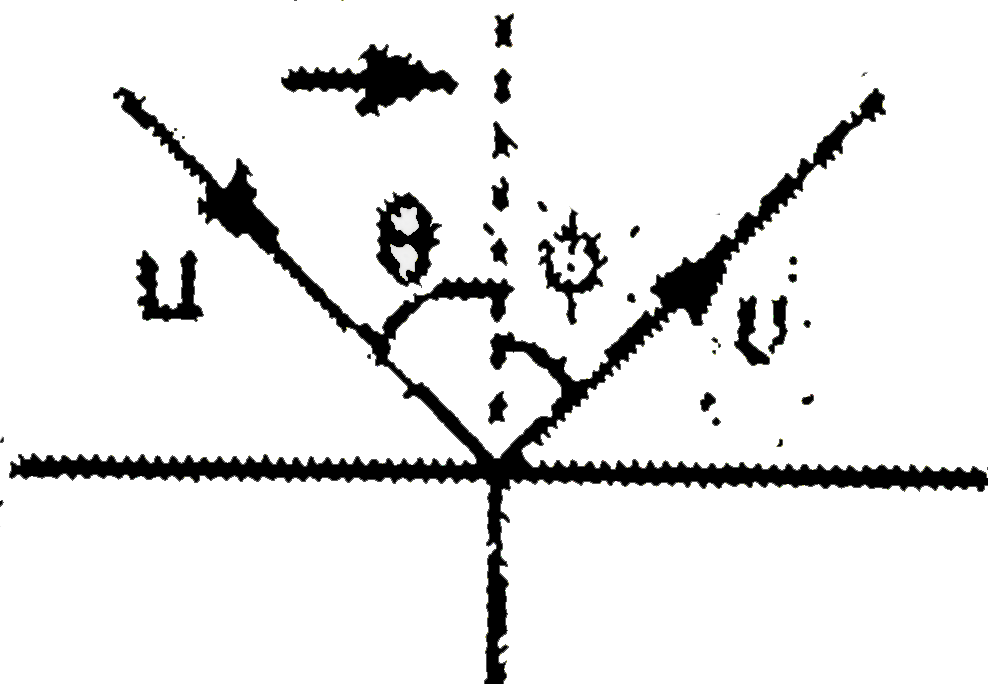
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle `theta` with the vertical, and rebounds with a speed `upsilon`, at an angle `phi` with the vertical. The coefficient of restitution between the particle and the floor is e. The angle `phi` is equal to :
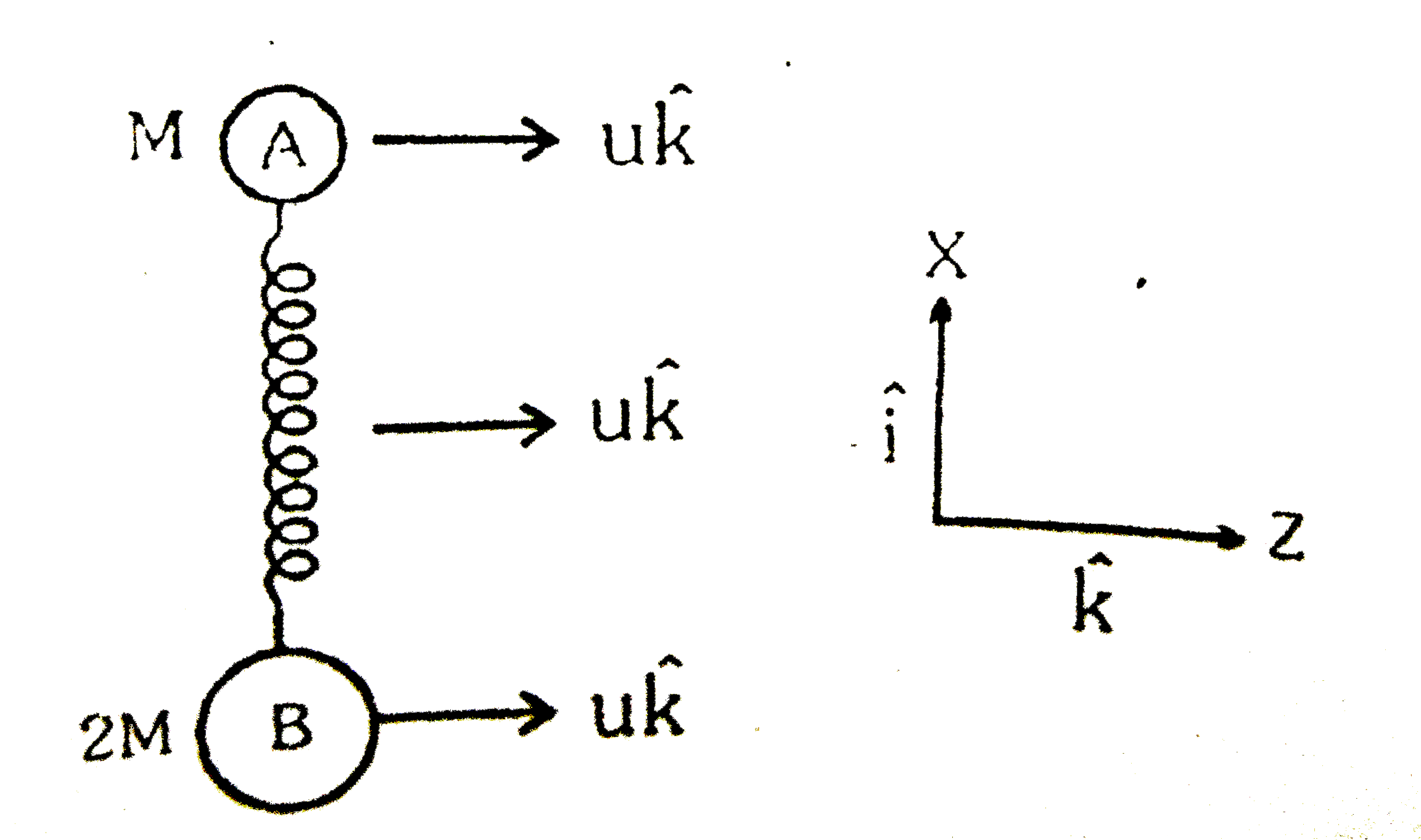
View SolutionTwo masses A and B of mass M and `2M` respectively are connected by a compressed ideal spring. The system in placed on a horizontal frictionless table and given a velocity `uhat(k)` in the z-direction as shown in the figure. The spring is then released. In the subsequent motion the line from B to A always points along the `hat(i)` unit vector. All some instant of time mass B has an x-component of velocity as `v_(x)hat(i)`. The velocity `vec(v)_(A)` of mass A at that instant is :-
View SolutionA particle A of mass 100 g moving along +ve x-axis with `10 m//sec`, collides at origin, with particle B of mass 200 gm moving along +ve y-axis with `10 m//sec`. After collision the particle B moves along line 4x-3y=0 with speed with speed `5 m//sec`. The equation of line along which A moves after collision.
View SolutionAn open water tight railway wagon of mass `5 xx 10^(3) kg` moves at an initial velocity `1.2 m//s` without friction on a railway track. Rain drops fall vertically downwards into the wagon. The velocity of the wagon after it has collected`10^(3) kg` of water will be :-
View SolutionTwo identical balls `A` and `B` lie on a smooth horizontal surface, which gradually merges into a curve to a height `3.2 m`. Ball `A` is given a velocity of `10 m//s`, to collide head-on with ball `B`, which then takes up the curved path. What is the minimum coefficient of restitution, `e`, for the collision between `A` and `B` in order that ball `B` reaches the highest point `C` of the curve.

View SolutionIf collision takes place between 2 particles then which of the following statement is/are true :
View SolutionOn a smooth horizontal plane, a uniform string of mass M and length L is lying in the state of rest. A man of the same mass M is standing next to one end of the string. Now, the man starts collecting the string. Finally the man collects all the string and puts it in his pocket. What is the displacement of the man with respect to earth in the process of collection ?

View SolutionIn the figure shown surface is frictionless and spring is in natural condition. If `x_(1), x_(2) " and " x_(3)` are the maximum compression in spring for elastic, completely inelastic and inelastic (e=0.5) respectively then :
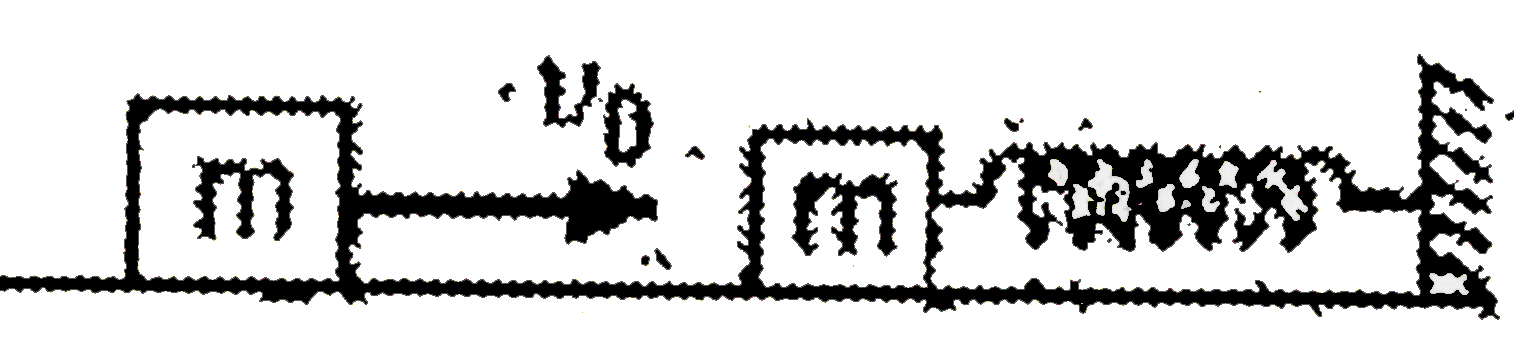
View SolutionIn a smooth stationary cart of length d, a small block is projected along it's length with velocity `upsilon` towards front. Coefficient of restitution for each collision is e. The cart rests on a smooth ground and can move freely. The time taken by block to come to rest w.r.t. cart is :

View SolutionIn the shown figure both blocks are in equilibrium m=1 kg. a bullet of mass m moves with velocity `10 m//s` and get embedded into the block A, then just after collision :
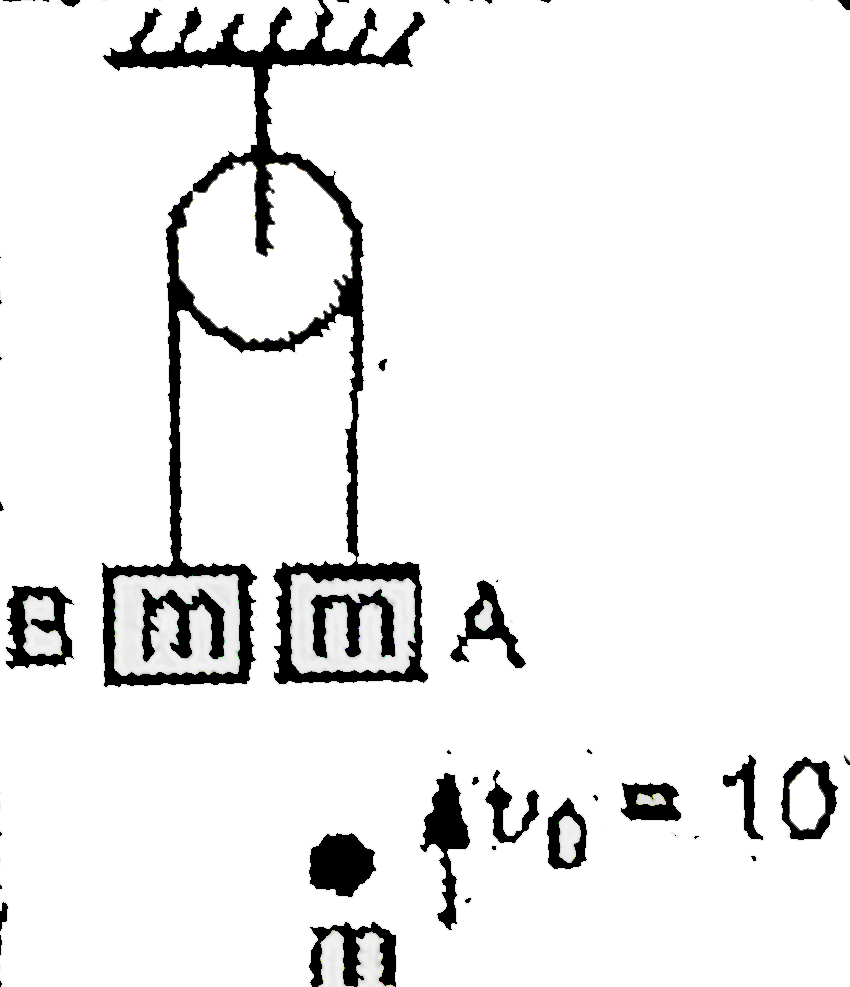
View SolutionIn the previous question the string will be tight again after 't' seconds from collision then t=
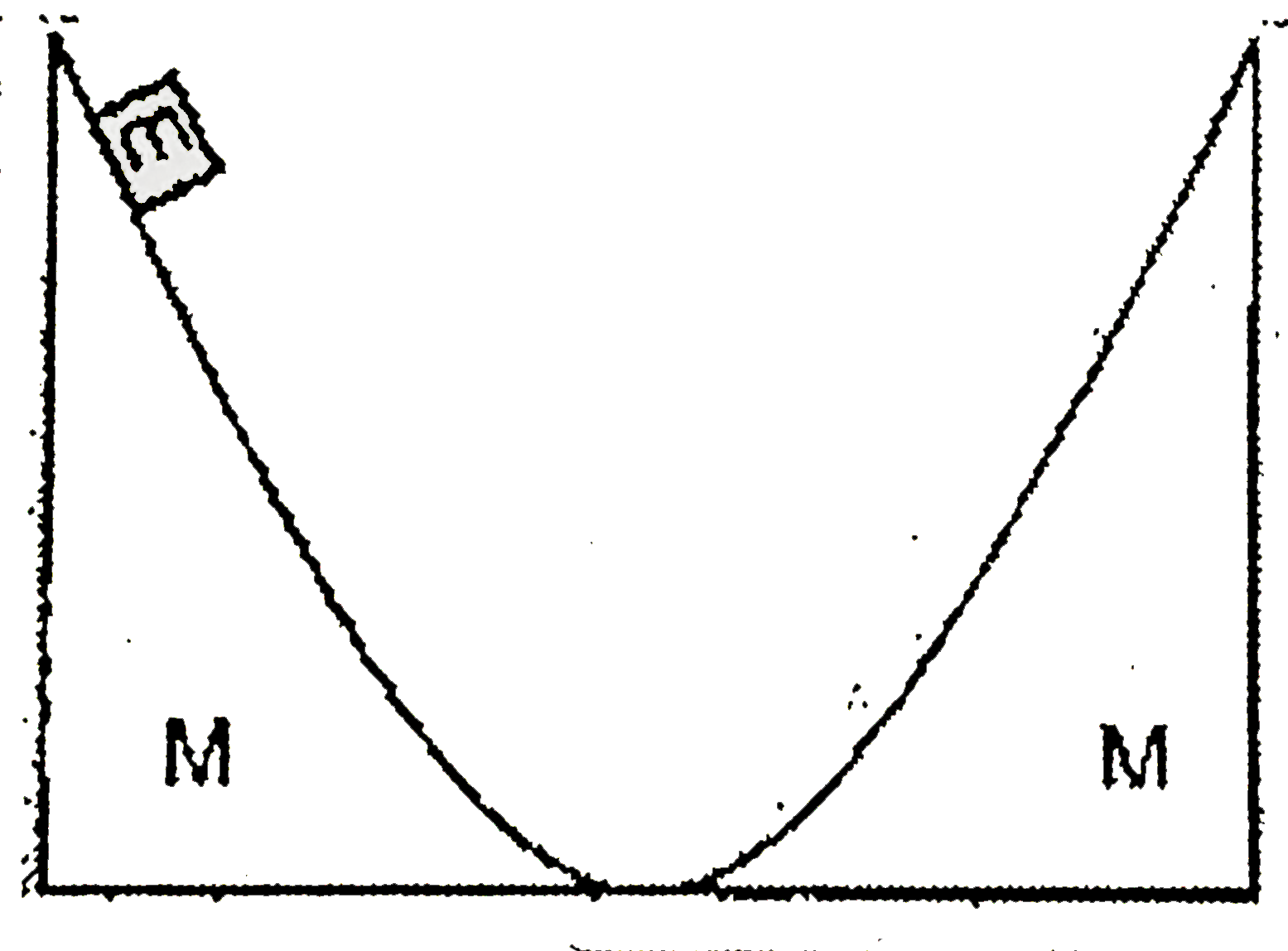
View SolutionThe inclined sufaces of two movable wedges of same mass M are smoothly conjugated with the horizontal plane as shown in figure. A washer of mass m slides down the left wedge from a height h. To what maximum height will the washer rise along the right wedge ? Neglect friction.
View SolutionIn the arrangements shown in the figure masses of each ball is `1 kg` and mass of trolley is `4 kg`. In the figure, shell of mass `1 kg` moving horizontally with velocity `v = 6 ms^(-1)` collides with the ball and get stuck to it then its maximum deflection of the thread (length `1.5 m`) with vertical

View SolutionCenter of mass of two thin uniform rods of same length but made up of different materials. & kept as shown, can be, if the meeting point is the origin of co-ordinated
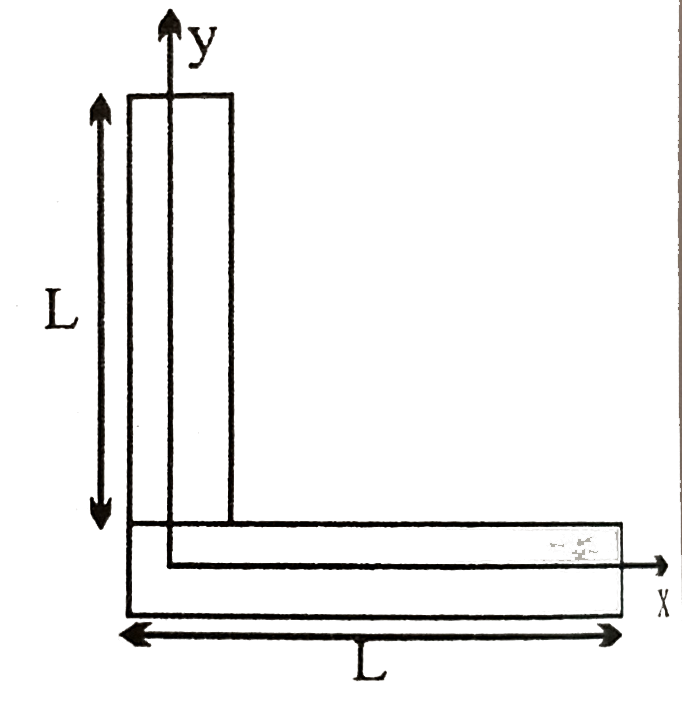
View SolutionA is a fixed point at height H above a perfectly inelastic smooth horizontal plane. A light inextesnsible string of length `L(gtH)` has one end attached to A and other to a heavy particle. The particle is held at the level of A with string just taut and released from rest. Find the height of the particle above the plane when it is next instaneously at rest .

View SolutionA hemisphere of mass 3m and radius R is free to slide with its base on a smooth horizontal table. A particle of mass m is placed on the top of the hemisphere. If particle is displaced with a negligible velocity, then find the anuglar velocity of the particle relative to the centre of the hemisphere at an angular displacement `theta`, when velocity of hemisphere is `upsilon`.
View SolutionTwo balls with masses in the ratio of 1:2 moving in opposite direction have a head-on elastic collision. If their velocities before impact were in the ration of 3:1, then velocities after impact will have the ratio :
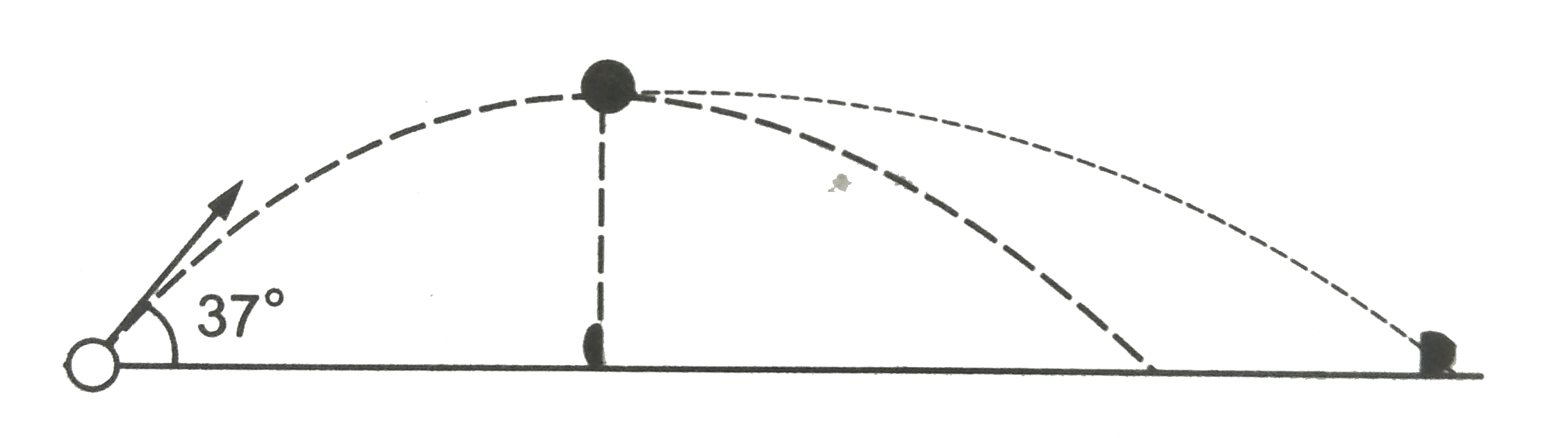
View SolutionA projectile is fired at a speed of 100 m/s at an angel of `37^0` above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Find the distance from the launching point to the where the heavier piece lands.
View SolutionTwo sphere `A` and `B` of equal masses lie on the smooth horizontal circular groove at opposite ends of diameter and at the end of time 't','A' impings on 'B' . If 'e' is the coefficient of restitution, the second impinge will occur after a time
View SolutionTwo blocks of masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of `14 m//s` to the heavier block in the direction of the lighter block. The velocity of the centre of mass is
View SolutionA stationary pulley carries a rope whose one end supports a ladder with a man and the other end the counterweight of mass M. The man of mass m climbs up a distance `l^'` with respect to the ladder and then stops. Neglecting the mass of the rope and the friction in the pulley axle, find the displacement `I` of the centre of inertia of this system.
View SolutionConsider the following two statements:
A The linear momentum of a particle is independent of the frame of reference.
B. The kinetic energy of a particle is independent of the frame of reference
View SolutionABC is a part of ring having radius `R_(2)` and ADC is a part of disc having inner radius `R_(1)` and outer `R_(2)`. Part ABC and ADC have same mass. Then center of mass will be located, from the centre.

View SolutionAt `t = 0`, the positions and velocities of two particles are as shown in the figure. They are kept on a smooth surface and being mutually attracted by gravitational force. Find the position of centre of mass at `t = 2s`.
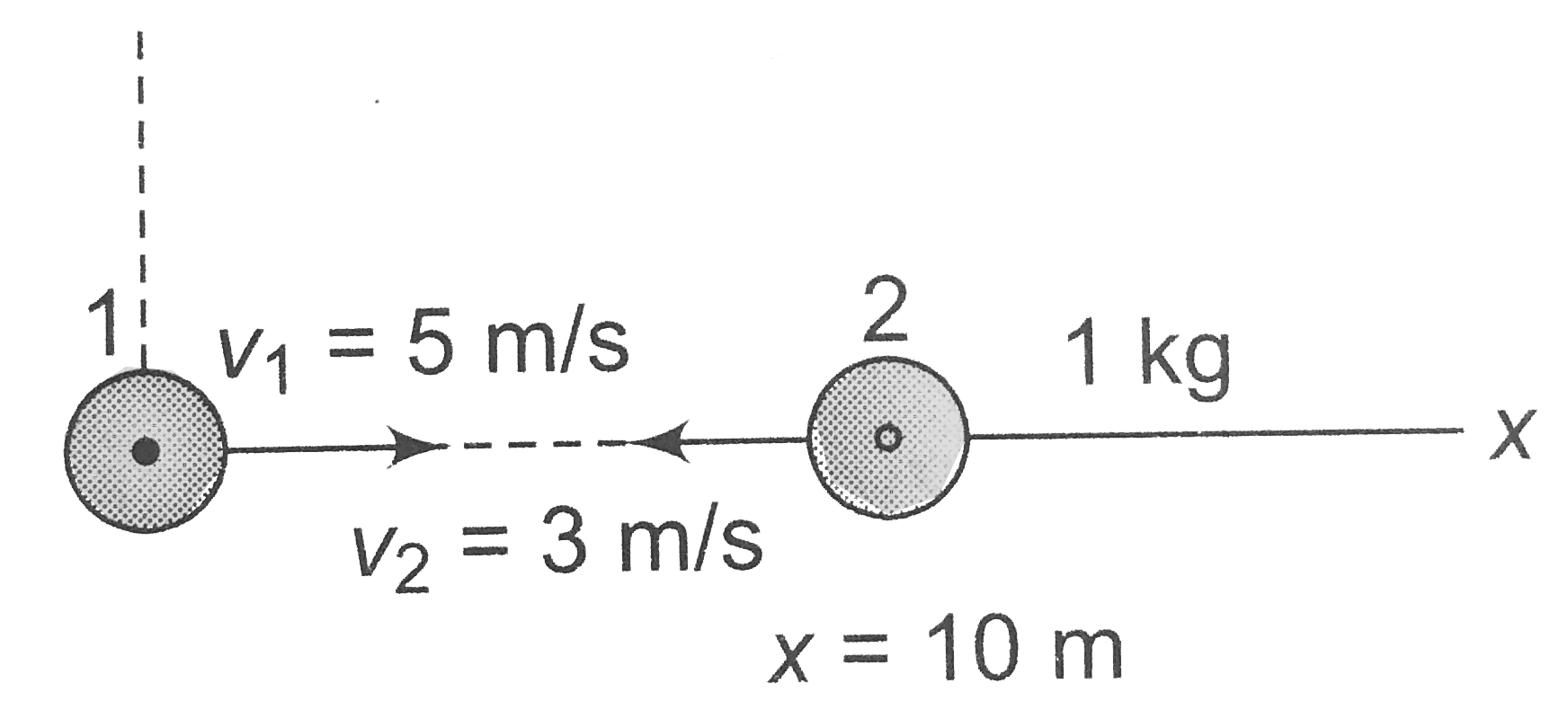 .
.
View SolutionTwo identical balls are dropped from the same height onto a hard surface, the second ball being released exactly when the first ball bollides with the surface. If the first ball has made two more collisions by the time the second one collides. Then the coefficient of restitution between the ball and the surface satisfies :
View SolutionA bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bulet emerges with speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction cioefficient between the block and the surface figure.

View SolutionA gun is mounted on a railroad car. The mass of the car, the gun, the shells and the operator is 50m where m is the mass of one shell. If the velocity of the shell with respect to the gun (in its state before firing) is 200 m/s, what is the recoil speed of the car after the second shot? Neglect friction.
View SolutionA man of mass 60 kg can throw a stone of mass 1 kg up to a height 5 m. If he is standing on ice skates of negligible mass, the maximum velocity that he can generate in same stone if he throus it with same force in the horizontal direction :
View SolutionThe density of a linear rod of length L varies as `rho=A+Bx` where x is the distance from the left end. Locate the centre of mass.

View SolutionThree identical balls are connected by light inextensible strings with each other as shown and rest over a smooth horizontal table. Length of each string is `l`.
At moment `t = 0`, ball `B` is imparted a velocity `v_(0)` perpendicular to the strings and then the system is left on its own.

Calculate the velocity of `B` just before `A` collides with ball `C`.
View SolutionIn above question 60 the velocity with which A colliides with C is :
View SolutionA box is put on a scale which is adusted to read zero when box is empty. A stream of pebbles is poured into the box from a height h above it's bottom at a rate `mu` pebbles/sec. each pebble has a mass m. Consider the collision between pebble and box to be completely inelastic. Find the reading of scale after t seconds of falling of pebbles.
View SolutionInitially spring is at it's natural length and collision is elastic. Then find maximum compression of spring during motion :
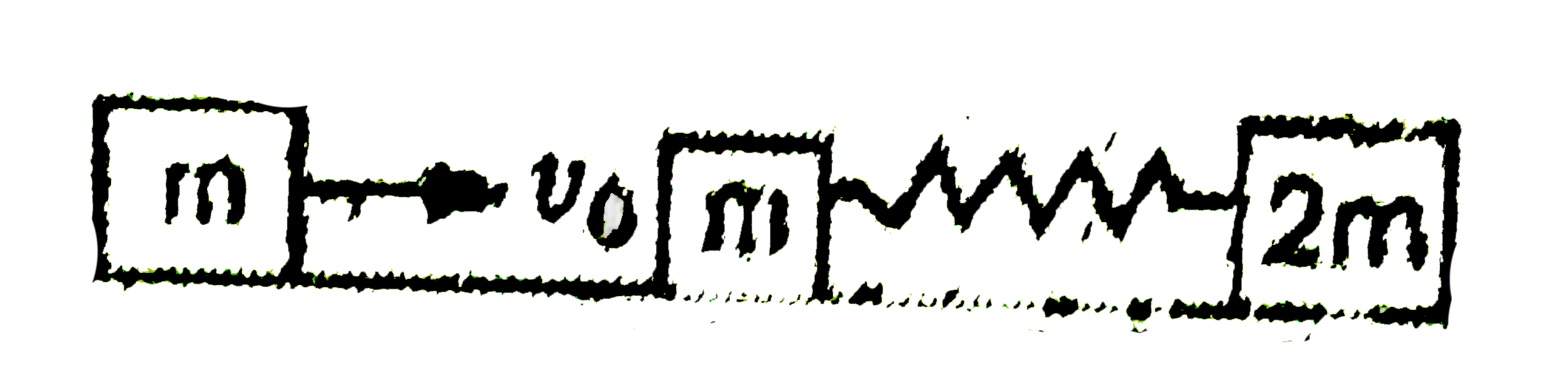
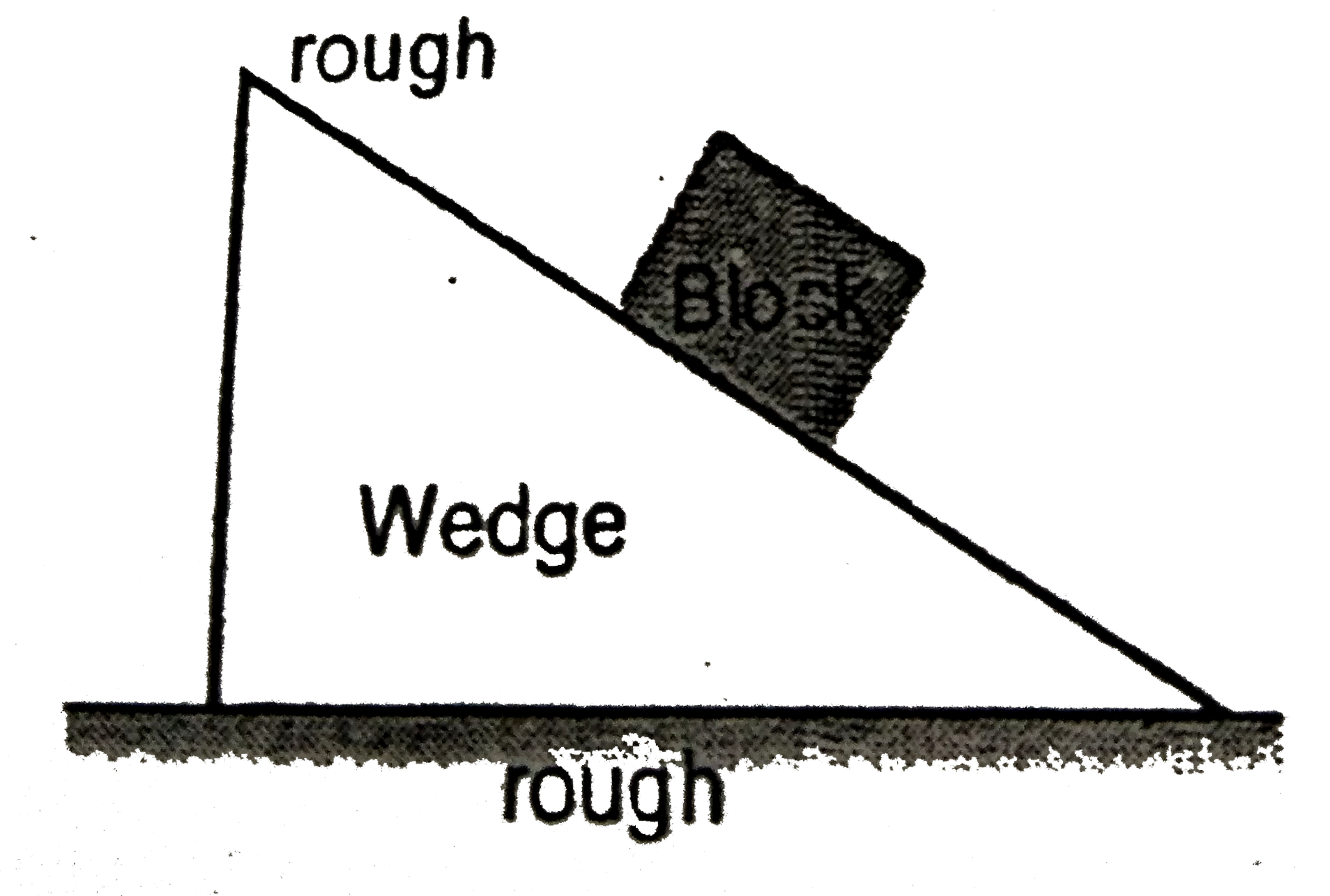
View SolutionWhen a block is placed on a wedge as shown in figure, the block starts sliding down and the wedge also start sliding on ground. All surfaces are rough. The centre of mass of `(` wedge `+` block `)` system will move.
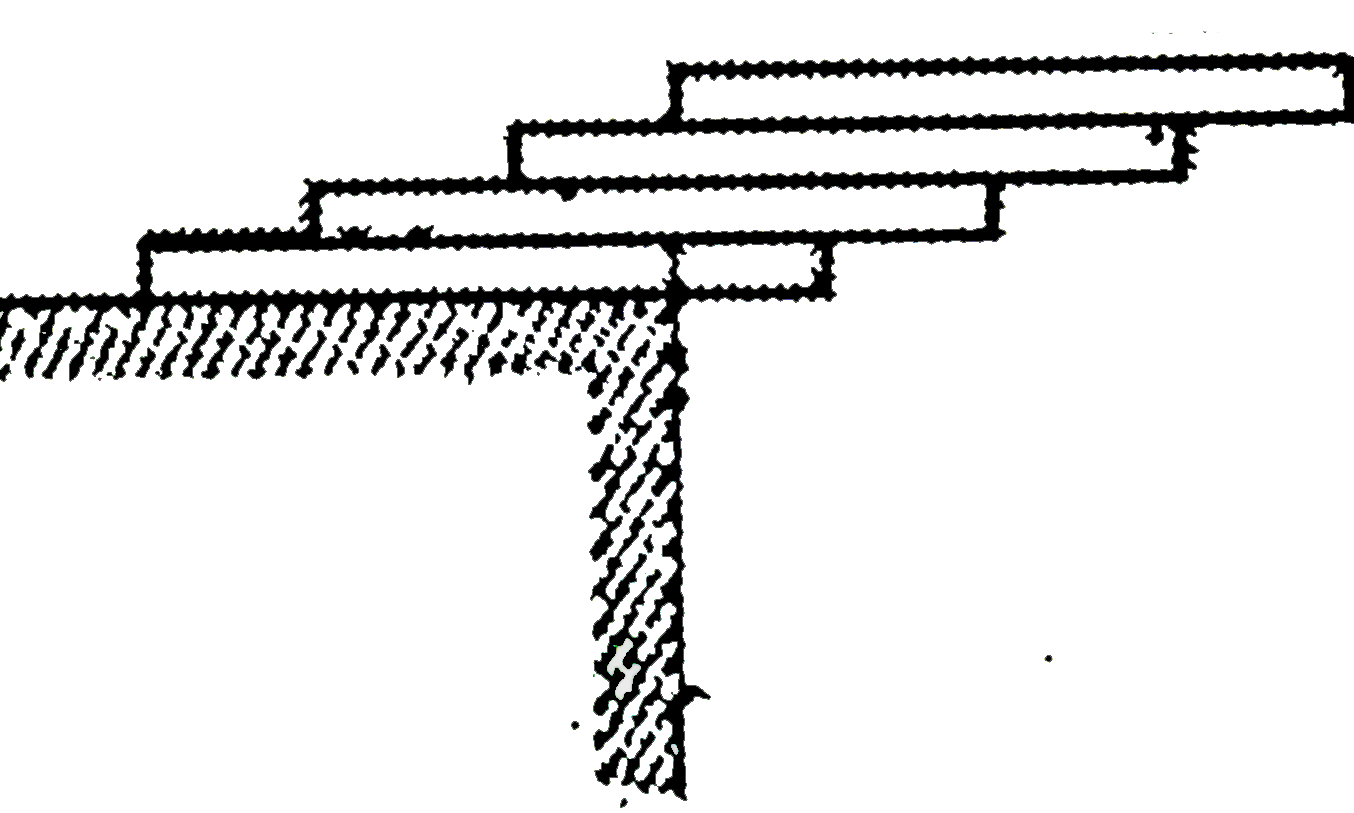
View SolutionFour identical rods of mass M and length L are placed on one another on the table so as to produce the maximum overhang as shown in figure. The maximum total overhang will be :
View SolutionA `20 g` bullet pierces through a plate of mass `M_(1) = 1 kg` and then comes to rest inside a second plate of mass `M_(2) = 2.98 kg` as shown in Fig. It is found that the two plates, initially at rest, now move with equal velocities. Find the percentage loss in the initial velocity of the bullet when it is between `M_(1)` and `M_(2`. Neglect any loss of material of the plates due to the action of bullet.
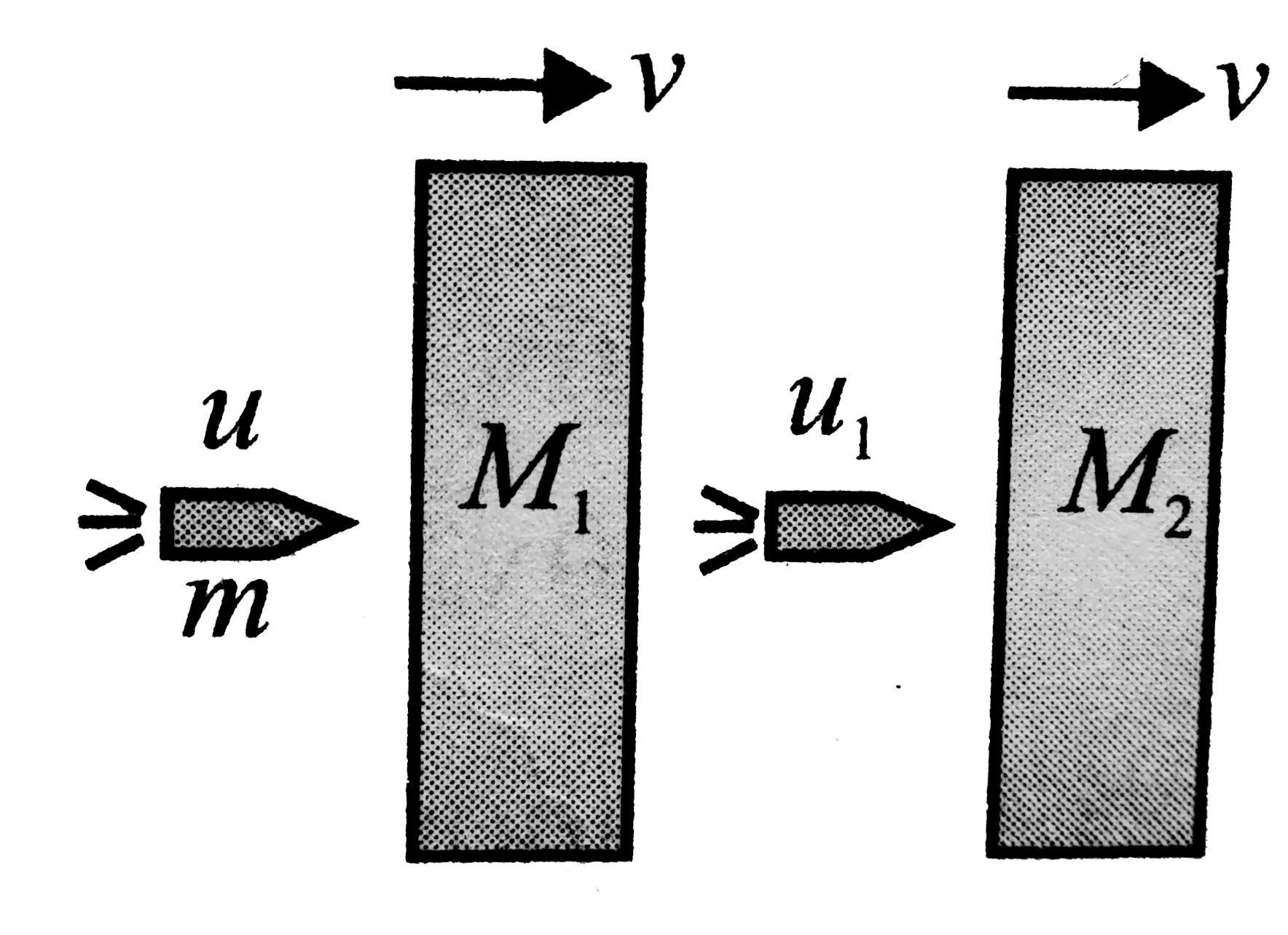
View SolutionTwo particles of masses `m_(1)` and `m_(2)` in projectile motion have velocities `vec(v)_(1)` and `vec(v)_(2)` , respectively , at time `t = 0`. They collide at time `t_(0)`. Their velocities become `vec(v')_(1)` and `vec(v')_(2)` at time ` 2 t_(0)` while still moving in air. The value of `|(m_(1) vec(v')_(1) + m_(2) vec(v')_(2)) - (m_(1) vec(v)_(1) + m_(2) vec(v)_(2))|`
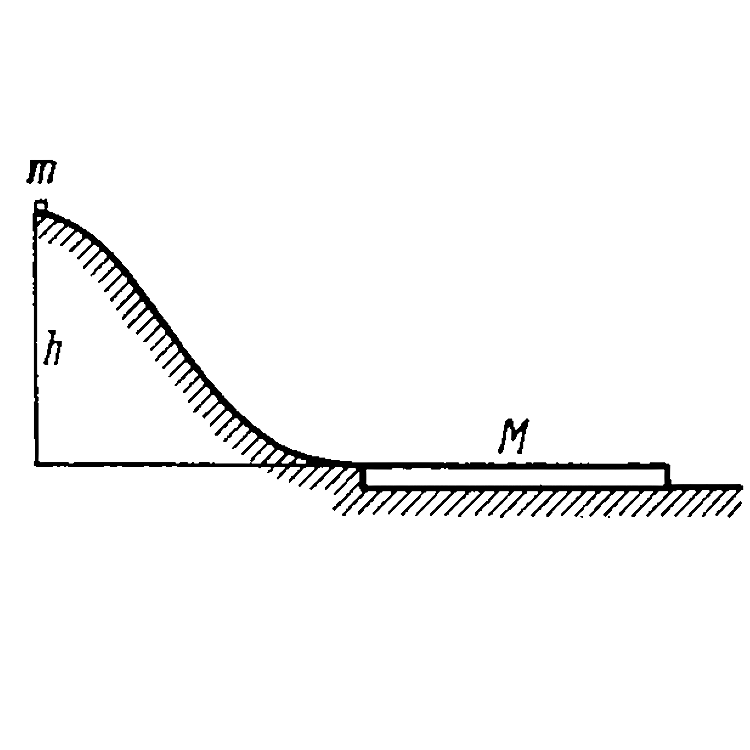
View SolutionA small disc of mass m slides down a smooth hill of height h without initial velocity and gets onto a plank of mass M lying on the horizontal plane at the base of the hill. (figure). Due to friction between the disc and the plank the disc slows down and, beginning with a certain moment, moves in one piece with the plank.
(1) Find the total work performed by the friction forces in this process.
(2) Can it be stated that the result of obtained does not depend on the choice of the reference frame?
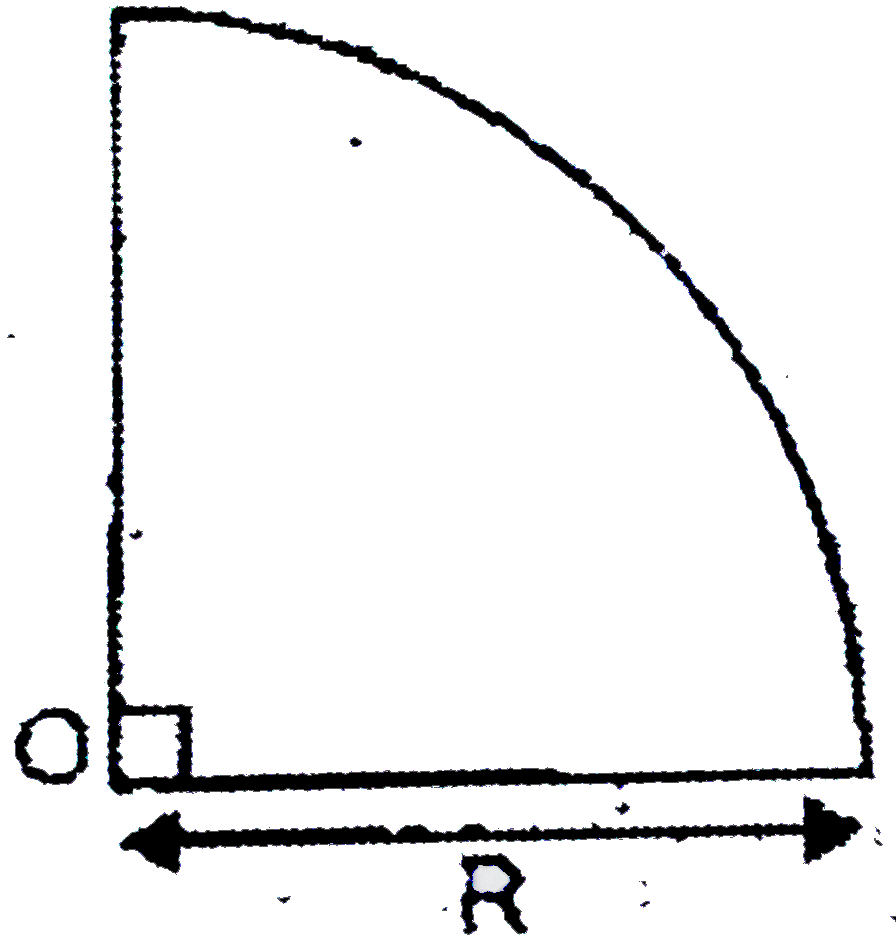
View SolutionIn the figure one fourth part of a uniform disc of radius R is shown. The distance of the centre of mass of this object from centre 'O' is :
View SolutionIn the figure shown a hole of radius 2 cm is made in a semicircular disc of radius `6pi` at a distance 8 cm from the centre C of the disc. The distance of the centre of mass of this system from point C is :

View SolutionWhen the momentum of a body increases by 100%, its K.E. increases by :
View SolutionA small sphere is moving at a constant speed in a vertical circle. Below is list of quantities that could be used to describe some aspect of the motion of the sphere.
I-kinetic energy
II- gravitational potential energy
III- momentum
Which of these quantities will change as this sphere moves around the circle ?
View SolutionFrom a uniform disc of radius R, an equilateral triangle of side `sqrt(3)R` is cut as shown in the figure. The new position of centre of mass is :

View SolutionA truck moving on horizontal road towards east with velocity `20ms^(1)` collides elastically with a light ball moving with velocity `25ms^(-1)` along west. The velocity of the ball just after collision
View SolutionFrom a circle of radius a, an isosceles right angles triangle with the hypotenuse as the diameter of the circle is removed. The distance of the centre of mass of the remaining portion from the centre of the circle is
View SolutionA particle of mass `4m` is projected from the ground at some angle with horizontal. Its horizontal range is `R`. At the highest point of its path it breaks into two pieces of masses `m` and `3m`, respectively, such that the smaller mass comes to rest. The larger mass finally falls at a distance `x` from the point of projection, where `x` is equal to
View SolutionTwo ball `A` and `B` having masses 1kg and 2kg, moving with speeds `21m//s` amd `4m//s` receptively in opposite direction, collide head on. After collision `A` moves with a speed of `1m//s` in the same direction, then correct statements is:
View SolutionTwo massless string of length 5 m hang from the ceiling very near to each other as shown in the figure. Two balls `A` and `B` of masses `0.25kg` and `0.5kg` are attached to the string. The ball `A` is released from rest at a height `0.45m` as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of ball `B` is `1 J` The velocity of ball `A` just after the collision is
Q01.png)
View SolutionAn ice block is melting at a constant rate `|(dm)/(dt)|=mu`. Its initial mass is `m_(0)` and it is moving with velocity on a frictionless horizontal surface. The distance travelled by it till it melts completely is :
View SolutionA ball strikes a smooth horizontal ground at an angle of `45^(@)` with the vertical. What cannot be the possible angle of its velocity with the vertical after the collisioin. (Assume `ele1`).
View SolutionTwo identical balls `A` and `B` are released from the position shown in Fig. They collide elastically with each other on the horizontal portion. The ratio of heights attained by `A` and `B` after collision is (neglect friction)

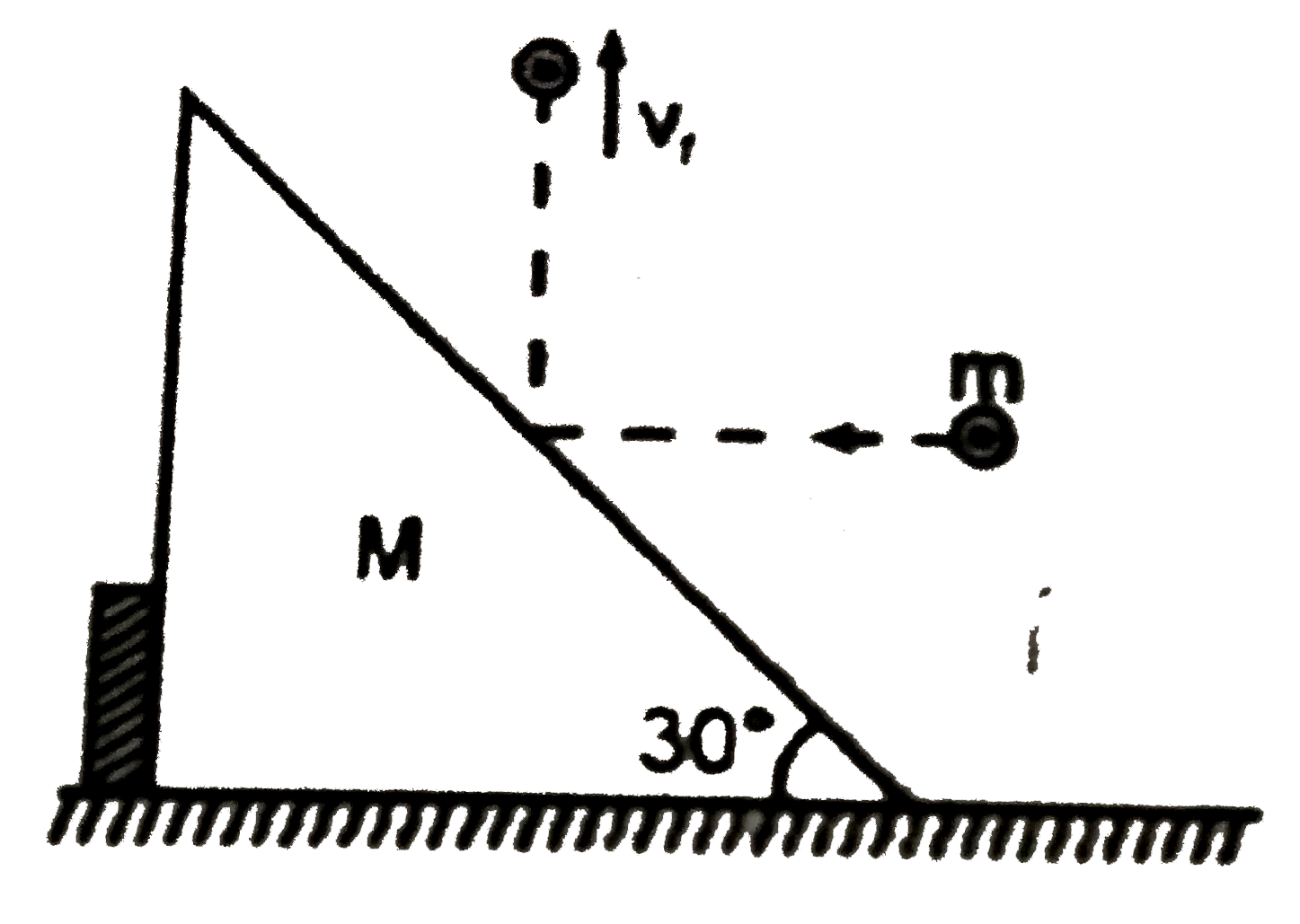
View SolutionAs shown in the figure a body of mass `m` moving horizontally with speed `sqrt(3) m//s` hits a fixed smooth wedge and goes up with a velocity `1v_(t)` in the vertical direction. If `/_` of wedge is `30^(@)`, the velocity `v_(f)` will be `:`
View SolutionThe system of the wedge and the block connected by a massless spring as shown in the figure is released with the spring in its natural length. Friction is absent. Maximum elongation in the spring will be
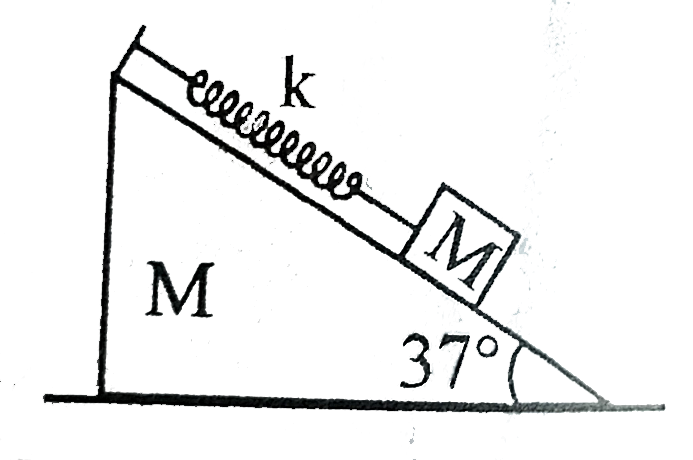
View SolutionA sphere is moving with velocity vector `2hati+2hatj` immediately before it hits a vertical wall. The wall is parallel to `hatj` and the coefficient of restitution of the sphere and the wall is `e=1/2`. Find the velocity of the sphere after it hits the wall?
View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is `M//3`, the distance that the man moves relative to the ground is
View SolutionTwo particles of equal mass have velocities `2hati ms^(-1) " and " 2hatj ms^(-1)`. First particle has an acceleration `(hati+hatj) ms^(-2)` while the acceleration of the second particle is zero. The centre of mass of the two particles moves in ?
View SolutionA man weighing 80 kg is standing at the centre of a flat boat and he is 20 m from the shore. He walks 8 m on the boat towards the shore and then halts.The boat weight 200 kg. How far is he from the shore at the end of this time ?
View SolutionA sphere strikes a wall and rebounds with coefficient of restitution `(1)/(3)`. If it rebounds with a velocity of `0.1 m//sec` at an angle of `60^(@)` to the normal to the wall, the loss of kinetic energy is :
View SolutionA spaceship travelling along `+y` axis with speed `v_(0)` suddenly shoots out one fourth of its parts with speed `2v_(0)` along `+x`-axis. `xy` axes are fixed with respect to ground. The velocity of the remaining part is
View SolutionIf linear density of a rod of length 3m varies as `lambda = 2 + x,` them the position of the centre of gravity of the rod is
View SolutionWhich of the following graphs represents the graphical relation between momentum (p) and kinetic energy (K) for a body in motion?
View SolutionA small bucket of mass `M` is attached to a long inextensible cord of length `L`. The bucket is released from rest when the cord is in a horizontal position. In its lowest position the bucket scoops up m of water, what is the height of the swing above the lowest position?
View SolutionA buggy of mass 100 kg is free to move on a frictionless horizontal track. Two men, each of mass 50 kg, are standing on the buggy, which is initially stationary. The men jump off the buggy with velocity =10m/s relative to the buggy. In one situation, the men jump one after the other. in another situation, the men jump simultaneously. what is the ratio of the velocities of the buggy in two cases?
View SolutionTwo men, of masses 60 kg and 80 kg are sitting at the ends of a boat of mass 60 and length 4 m. the boat is stationary. If the men now exchange their position, then:
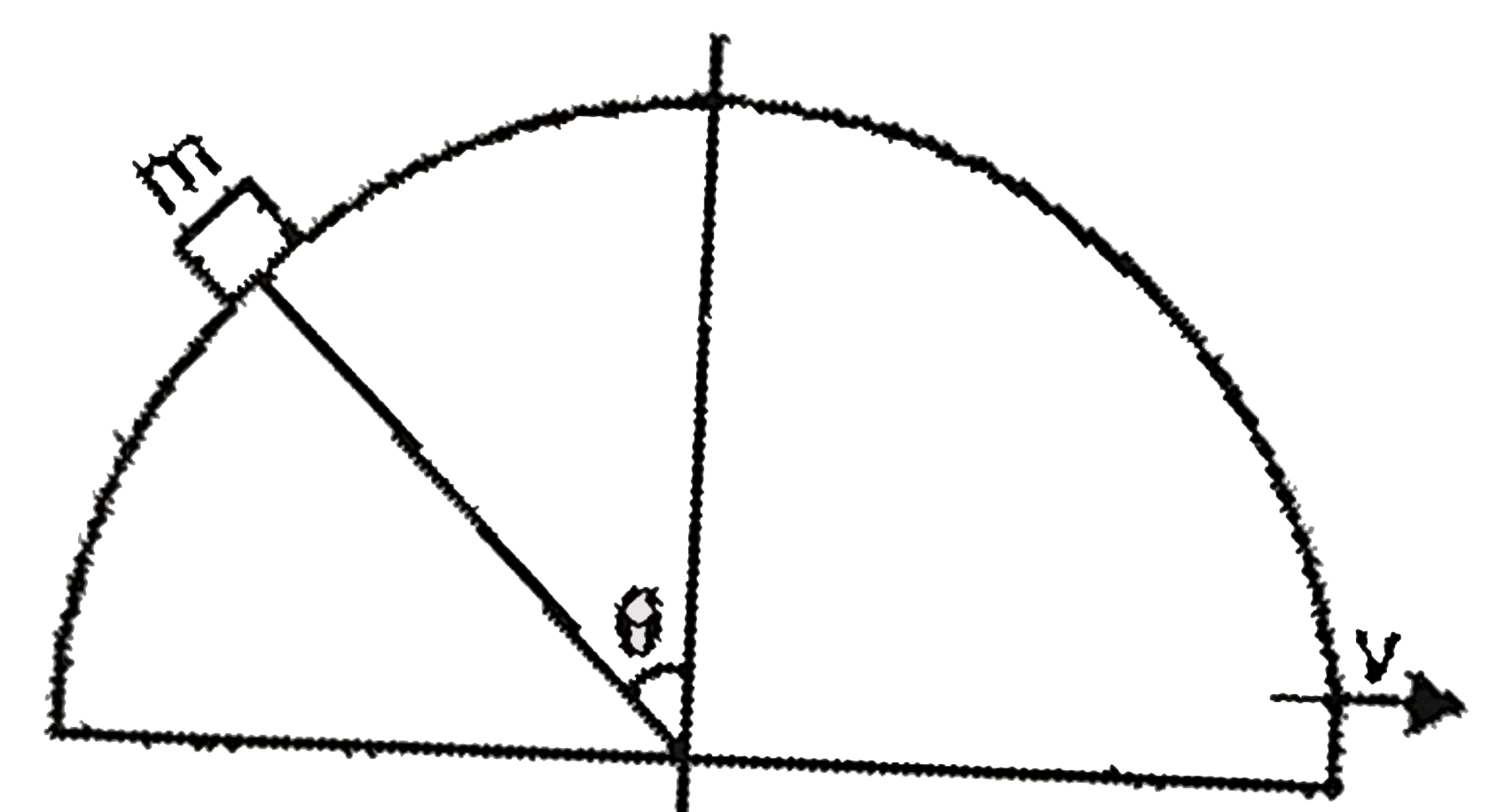
View SolutionA billiard table whose length and width are as shown in the figure. A ball is placed at point A. at what angle `theta` the ball be projected so that after colliding with two walls, the ball will fall in the pocket B? assume that all collisions are perfectly elastic: (neglect friction)

View SolutionIn the above, suppose that the smaller ball does not stop after collision, but continues to move downwards with a speed `=(upsilon_(0))/(2)` after the collision. Then, the speed of each bigger ball after collision is
View SolutionA body of mass `m` is dropped from a height of `h`. Simultaneously another body of mass `2m` is thrown up vertically with such a velocity `v` that they collide at height `h/2`. If the collision is perfectly inelastic, the velocity of combined mass at the time of collision with the ground will be
View SolutionIn the figure (i), (ii) and (iii) shown the objects, A,B and C are of same mass. String, spring and pulley are massless. C strikes B with velocity `u` in each case and stricks to it. The ratio of velocity of B in case (i) to (ii) to (iii) is-

View SolutionA force exerts an impulse Ion a particle changing its speed from initial velocity `u` to final velocity `2u`. The applied force and the initial velocity are oppositely oriented along the same line. The work done by the force is
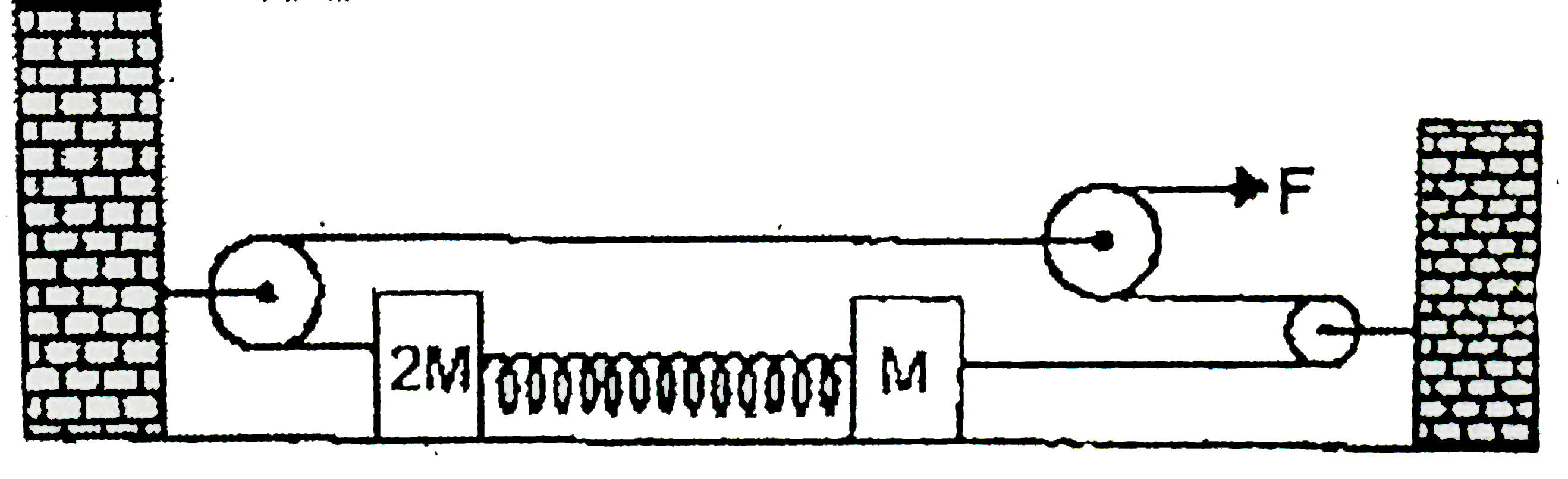
View SolutionIn the diagram shown, no friction at any contact surface. Initially, the spring has no deformation what will be the maximum deformation in the spring? Consider all the strings to be sufficiency large. Consider the spring constant to be K.
View Solution
Level 1 questions and complete solutions for chapter IMPULSE AND MOMENTUM of SHREE BALAJI PHYSICS (HINGLISH) of Class 11