Complete Solutions to COMPREHENSION_TYPE of chapter RIGID BODY MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | RIGID BODY MOTION |
| ANURAG MISHRA | COMPREHENSION_TYPE |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
A solid cylinder of mass `m` rolls on a rough surface with velocity `v_(0)`. It collides elastically with a cubical block of same mass at rest. The centre of mass of both the bodies are at same height. Coefficient of friction between horizontal surface and cylinder as well as horizontal surface and cube is `mu`. No frictional exists between cylinder and cube. The cylinder collides the, cube at `t = 0`, then.

Percentage of energy of cylinder lost due to collision is:
View SolutionA solid cylinder of mass `m` rolls on a rough surface with velocity `v_(0)`. It collides elastically with a cubical block of same mass at rest. The centre of mass of both the bodies are at same height. Coefficient of friction between horizontal surface and cylinder as well as horizontal surface and cube is `mu`. No frictional exists between cylinder and cube. The cylinder collides the, cube at `t = 0`, then.
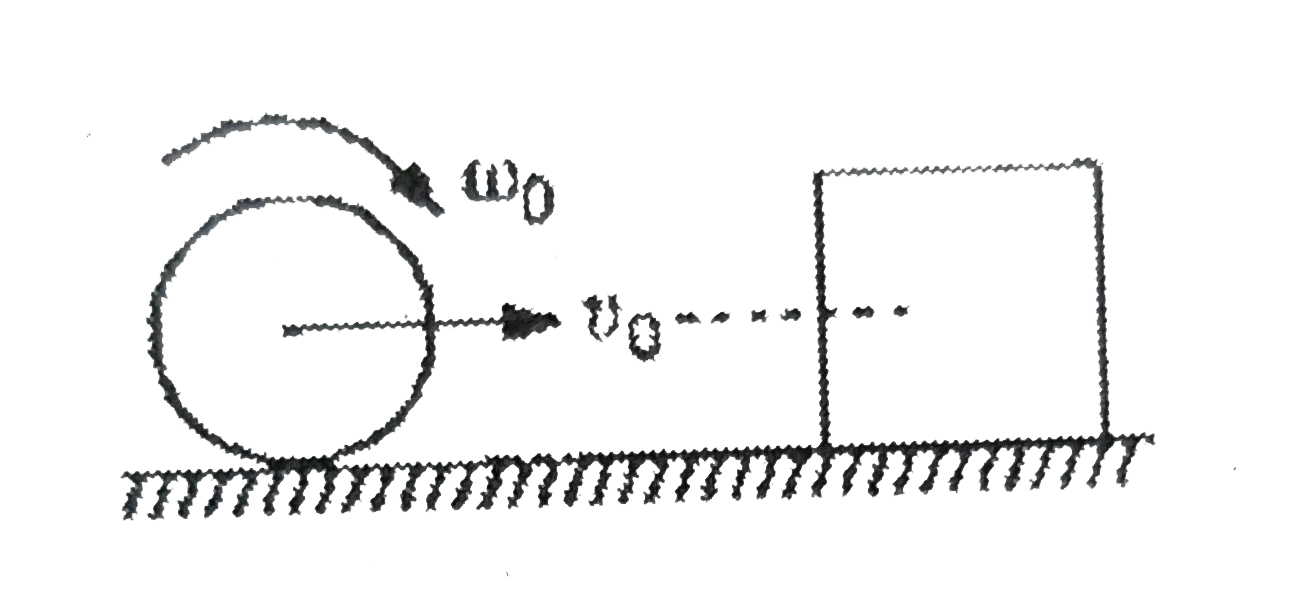
Regarding frictional force acting on cylinder we can say that:
View SolutionA solid cylinder of mass `m` rolls on a rough surface with velocity `v_(0)`. It collides elastically with a cubical block of same mass at rest. The centre of mass of both the bodies are at same height. Coefficient of friction between horizontal surface and cylinder as well as horizontal surface and cube is `mu`. No frictional exists between cylinder and cube. The cylinder collides the, cube at `t = 0`, then.
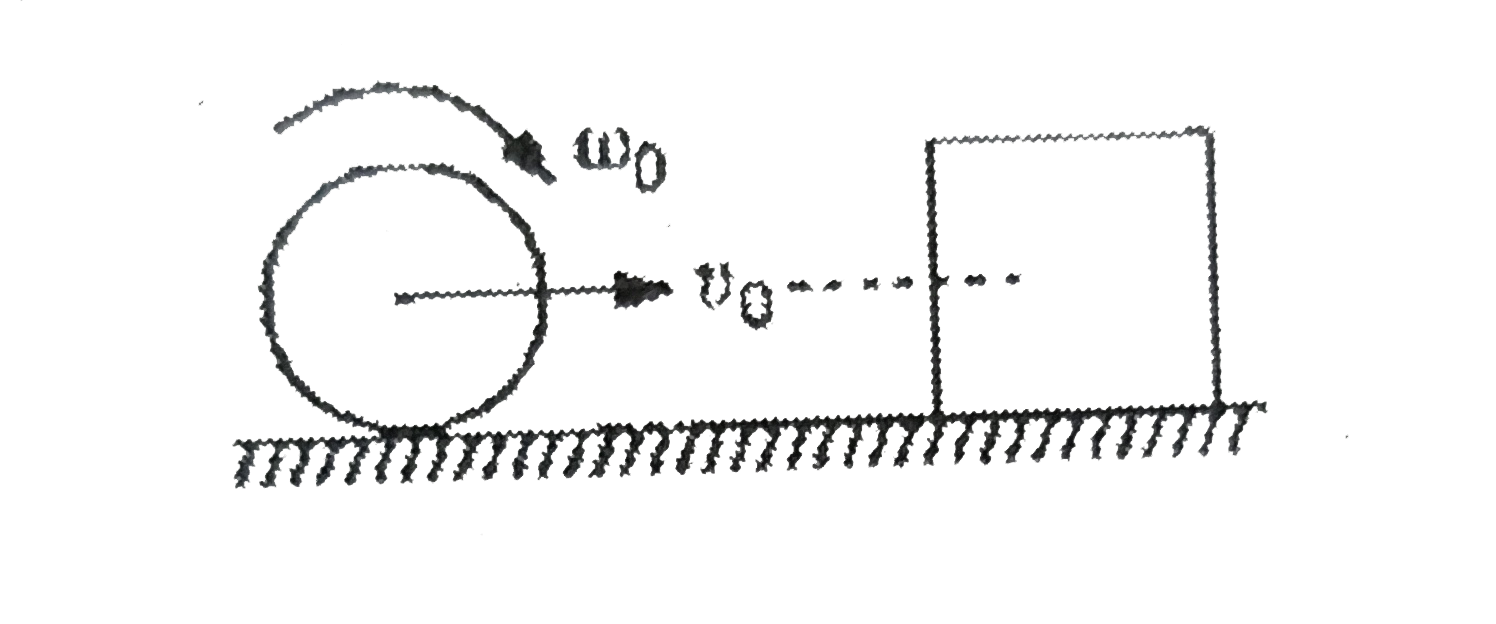
Time after which the cylinder starts pure rolling again:
View SolutionA solid cylinder of mass `m` rolls on a rough surface with velocity `v_(0)`. It collides elastically with a cubical block of same mass at rest. The centre of mass of both the bodies are at same height. Coefficient of friction between horizontal surface and cylinder as well as horizontal surface and cube is `mu`. No frictional exists between cylinder and cube. The cylinder collides the, cube at `t = 0`, then.
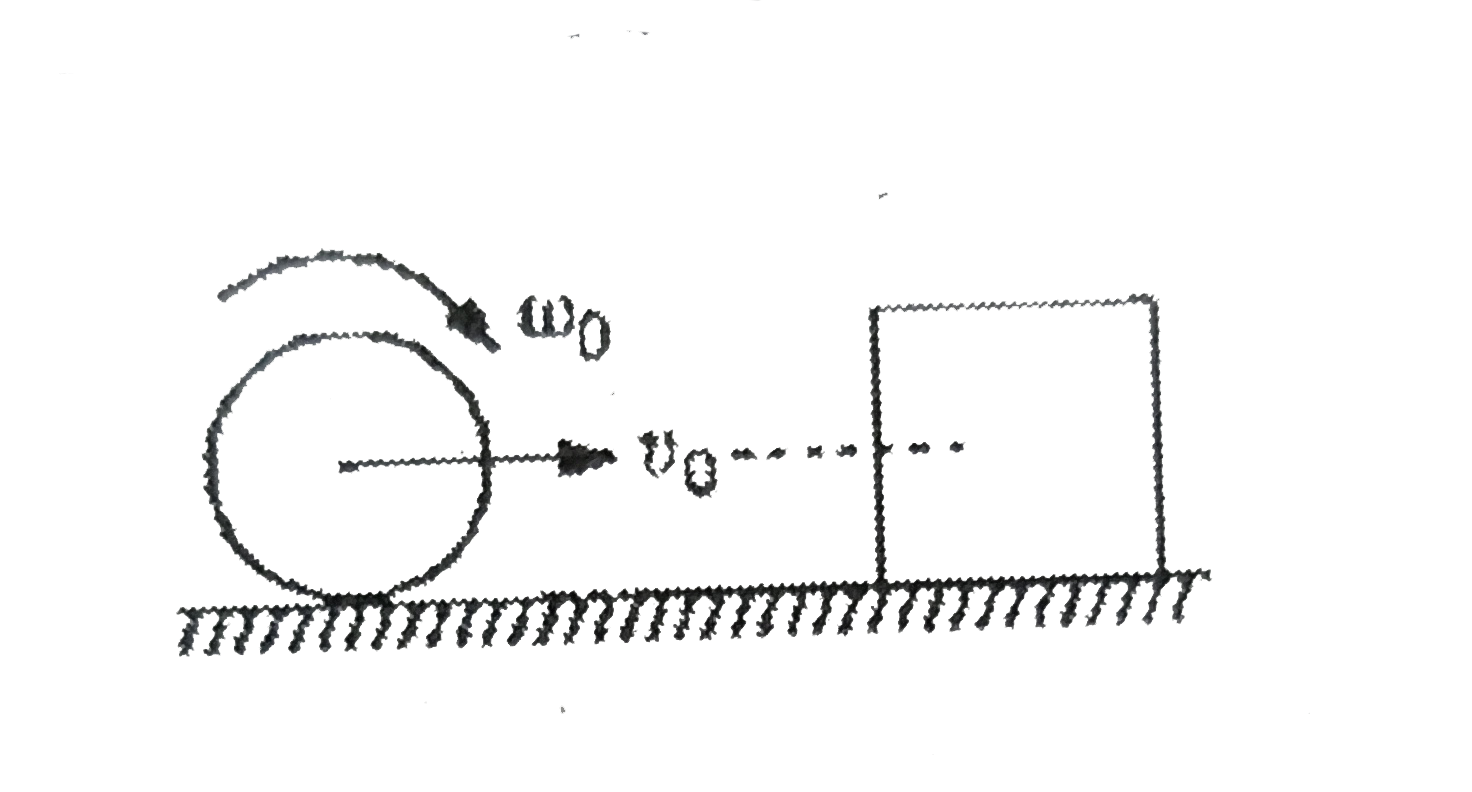
Velocity of cube when the cylinder starts pure rolling:
View SolutionA solid cylinder of mass `m` rolls on a rough surface with velocity `v_(0)`. It collides elastically with a cubical block of same mass at rest. The centre of mass of both the bodies are at same height. Coefficient of friction between horizontal surface and cylinder as well as horizontal surface and cube is `mu`. No frictional exists between cylinder and cube. The cylinder collides the, cube at `t = 0`, then.

Velocity of cylinder with which it will collide with cube again is:
View SolutionA solid cylinder of mass `m` rolls on a rough surface with velocity `v_(0)`. It collides elastically with a cubical block of same mass at rest. The centre of mass of both the bodies are at same height. Coefficient of friction between horizontal surface and cylinder as well as horizontal surface and cube is `mu`. No frictional exists between cylinder and cube. The cylinder collides the, cube at `t = 0`, then.

Maximum separation between cylinder before it collide the cube again is:
View SolutionA uniform rod mass `m` and length `L` is free to rotate about hinge `O`. A slight disturbance cause the rod to rotate freely about `O` and it strikes the ground.

Velocity with which the non-hinged end of rod strikes the surface is:
View SolutionA uniform rod mass `m` and length `L` is free to rotate about hinge `O`. A slight disturbance cause the rod to rotate freely about `O` and it strikes the ground.
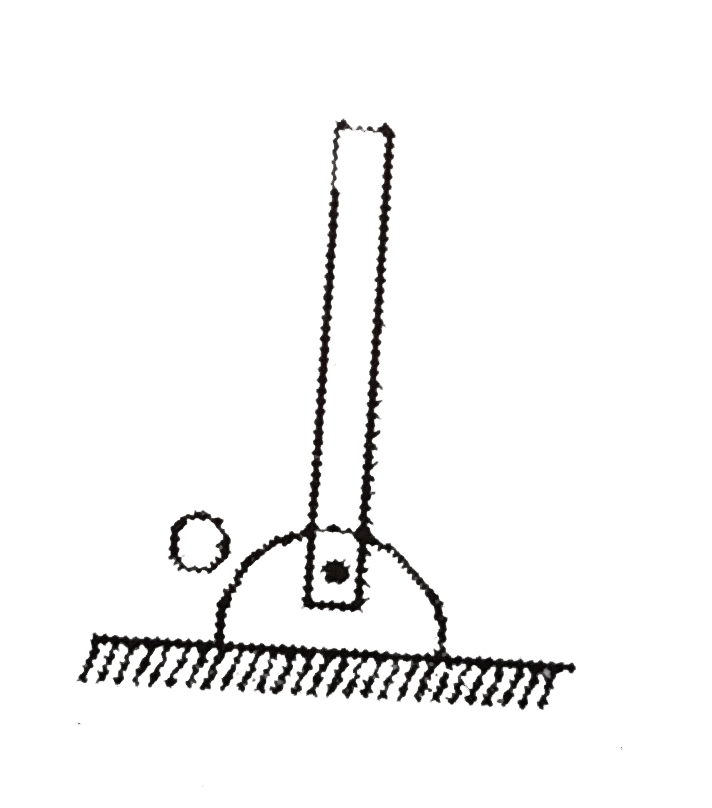
Horizontal force applied on rod by hinge just before the rod hits the surface is:
View SolutionA uniform rod mass `m` and length `L` is free to rotate about hinge `O`. A slight disturbance cause the rod to rotate freely about `O` and it strikes the ground.
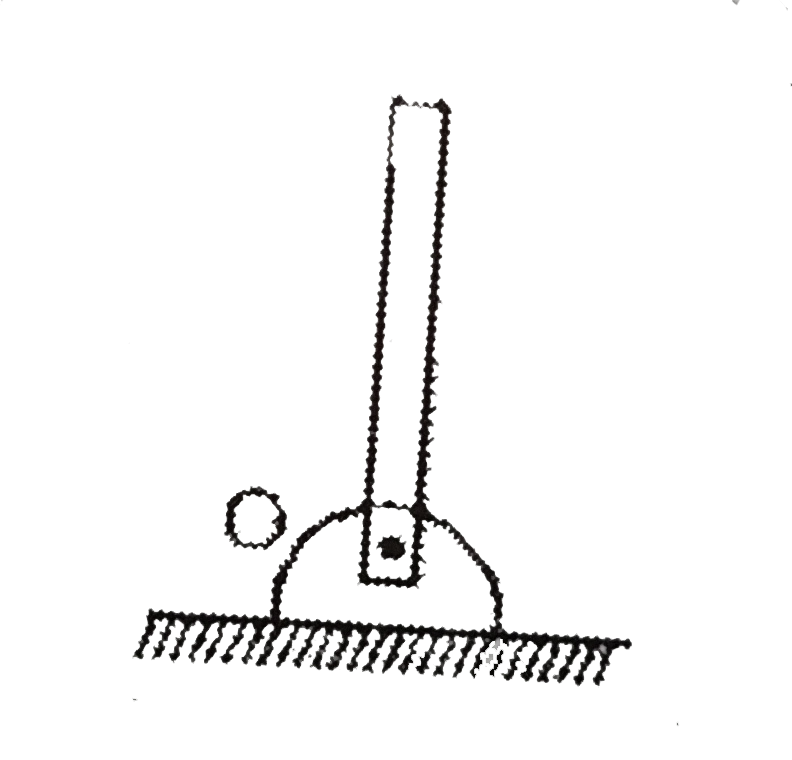
Vertical force applied by hinge on rod at the moment it strikes the ground is:
View SolutionA spool of mass `m` has moment of inertia `I= 2mR^(2)` about its axis of symmetry. The inner and outer radius of spool `R` and `2R` respectively. Thread is wounded on the inner cylinder and its one end is pulled a force F acting at angle `theta` with horizontal. The surface is sufficiently rough and th.e spool never slides on the surface.

For `theta=0^(@)`, the acceletation of spool is
View SolutionA spool of mass `m` has moment of inertia `I= 2mR^(2)` about its axis of symmetry. The inner and outer radius of spool `R` and `2R` respectively. Thread is wounded on the inner cylinder and its one end is pulled a force F acting at angle `theta` with horizontal. The surface is sufficiently rough and th.e spool never slides on the surface.

For `theta=60^(@)` the acceleration of spool is
View SolutionA spool of mass `m` has moment of inertia `I= 2mR^(2)` about its axis of symmetry. The inner and outer radius of spool `R` and `2R` respectively. Thread is wounded on the inner cylinder and its one end is pulled a force `F` acting at angle `theta` with horizontal. The surface is sufficiently rough and th.e spool never slides on the surface.
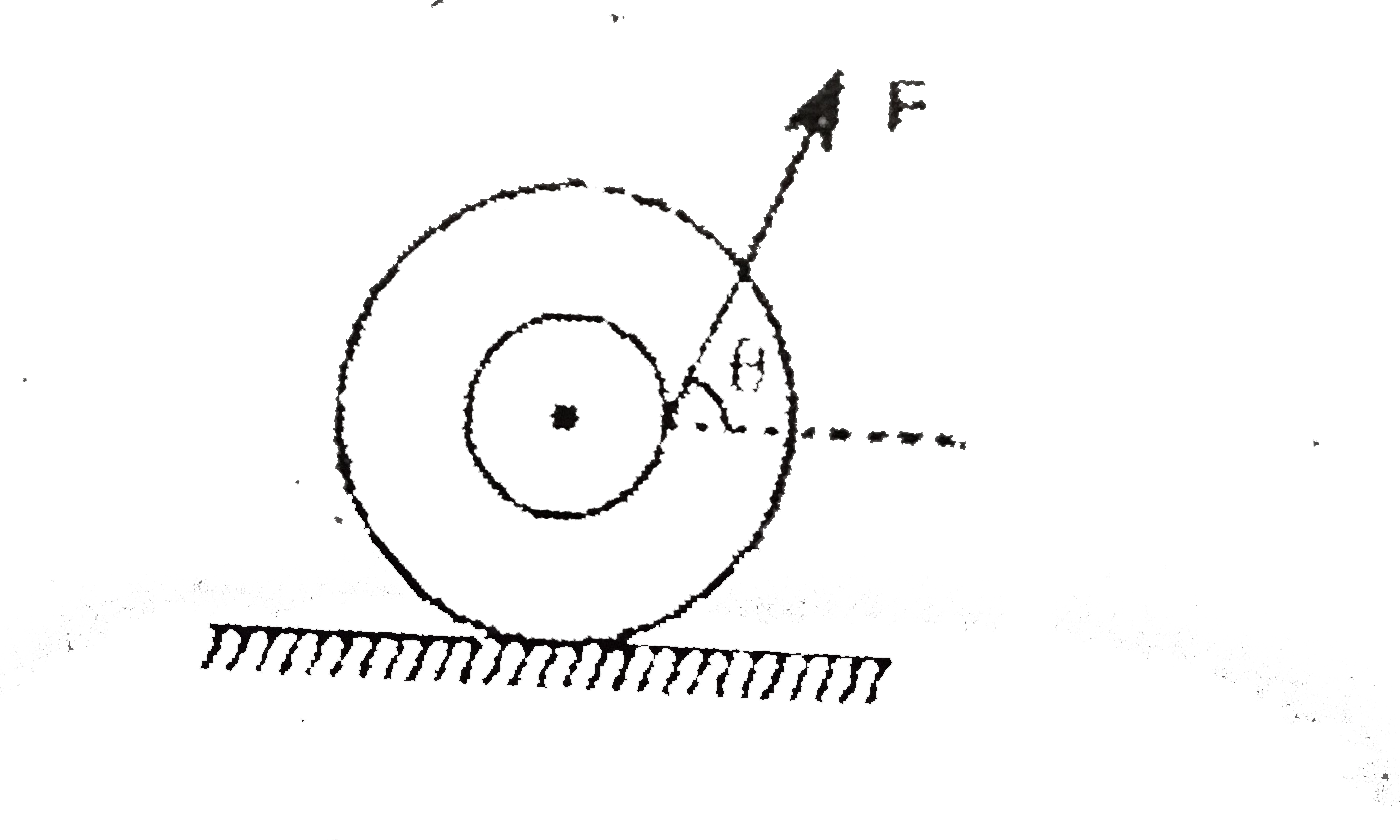
Regarding to the direction of frictional force, which of the following statement is correct?
View SolutionA spool of mass `m` has moment of inertia `I= 2mR^(2)` about its axis of symmetry. The inner and outer radius of spool `R` and `2R` respectively. Thread is wounded on the inner cylinder and its one end is pulled a force F acting at angle `theta` with horizontal. The surface is sufficiently rough and th.e spool never slides on the surface.

Regarding to the direction of rotation of spool which of the following statement is true?
View SolutionA spool of mass `m` has moment of inertia `I= 2mR^(2)` about its axis of symmetry. The inner and outer radius of spool `R` and `2R` respectively. Thread is wounded on the inner cylinder and its one end is pulled a force F acting at angle `theta` with horizontal. The surface is sufficiently rough and th.e spool never slides on the surface.

Maximum frictional force acting on the spool is:
View SolutionA spool of mass `m` has moment of inertia `I= 2mR^(2)` about its axis of symmetry. The inner and outer radius of spool `R` and `2R` respectively. Thread is wounded on the inner cylinder and its one end is pulled a force F acting at angle `theta` with horizontal. The surface is sufficiently rough and th.e spool never slides on the surface.

Maximum frictional force acting on the spool is:
View SolutionA string wrapped around a cyliner of mass `m` and radius `R`. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
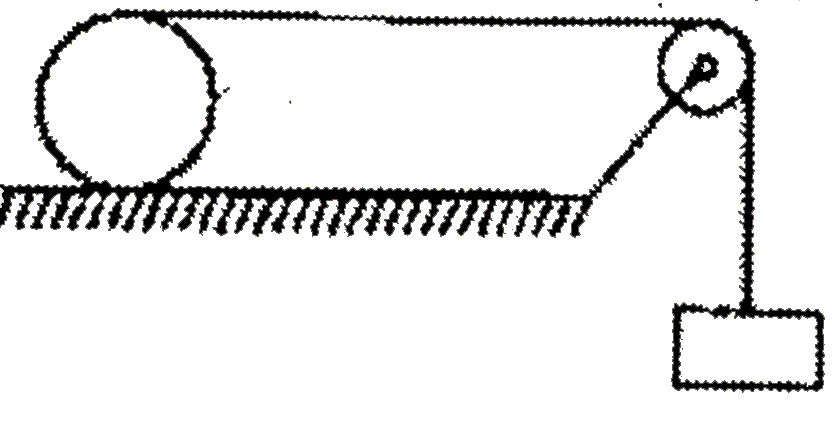
Acceleration of hanging mass is:
View SolutionA string wrapped around a cyliner of mass `m` and radius `R`. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
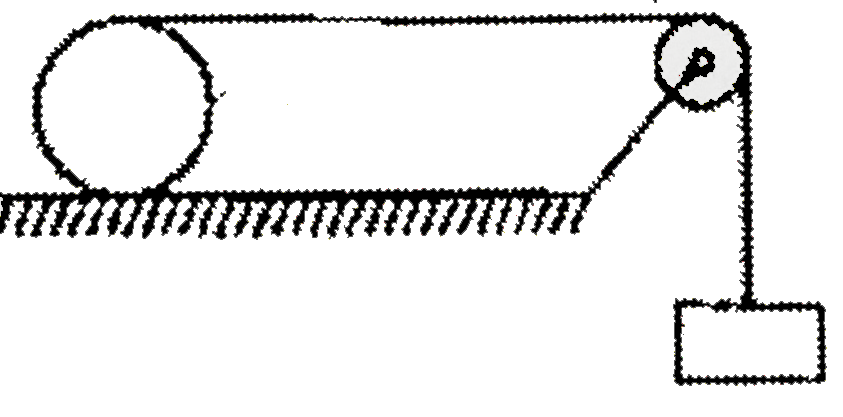
Acceleration of cylinder is:
View SolutionA string wrapped around a cyliner of mass `m` and radius `R`. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
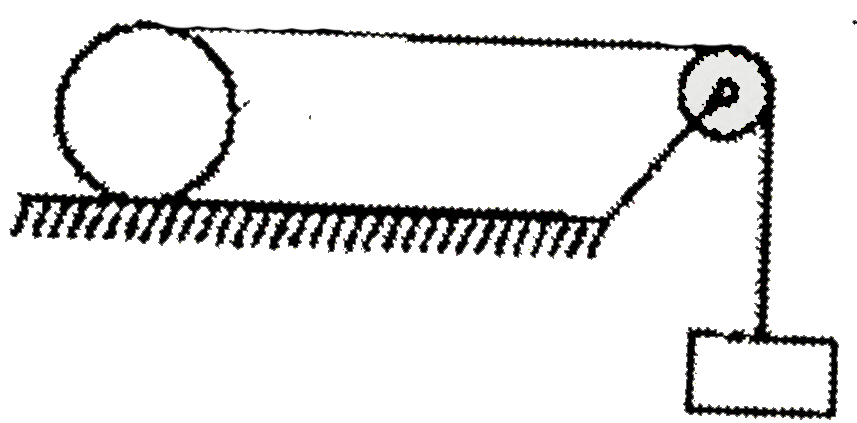
Distance moved by cylinder during time taken by it to complete one rotation is:
View SolutionA string wrapped around a cylinder of mass `m` and radius `R`. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
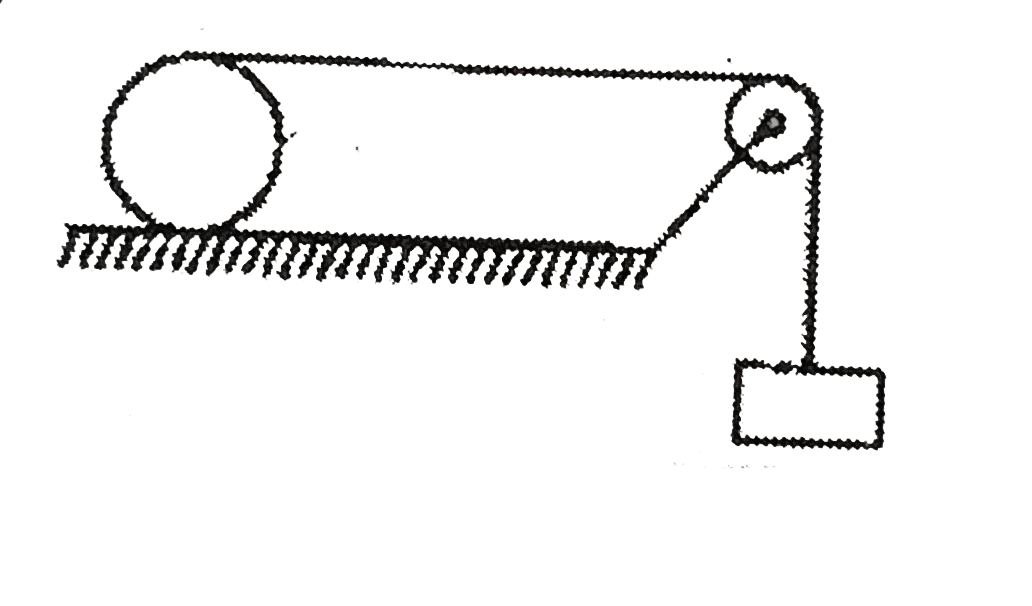
Distance moved by hanging mass during the above time interval is:
View SolutionA string wrapped around a cyliner of mass `m` and radius `R`. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
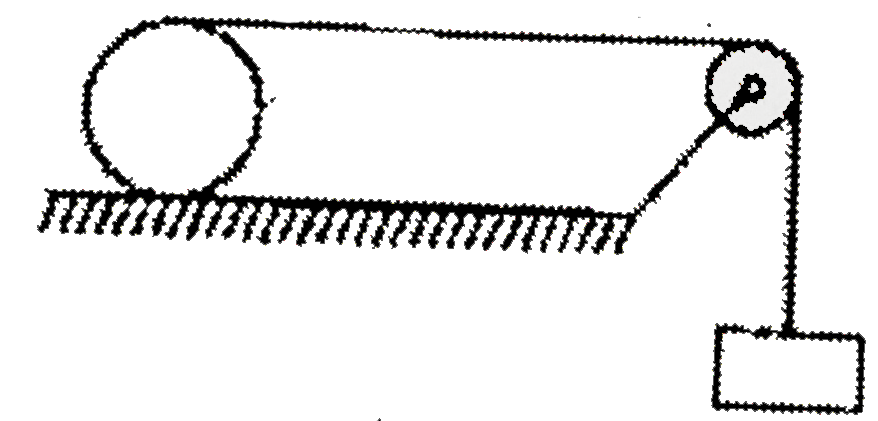
Velocity of point of contact 'of cylinder at this moment is:
View SolutionA string wrapped around a cyliner of mass `m` and radius `R`. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
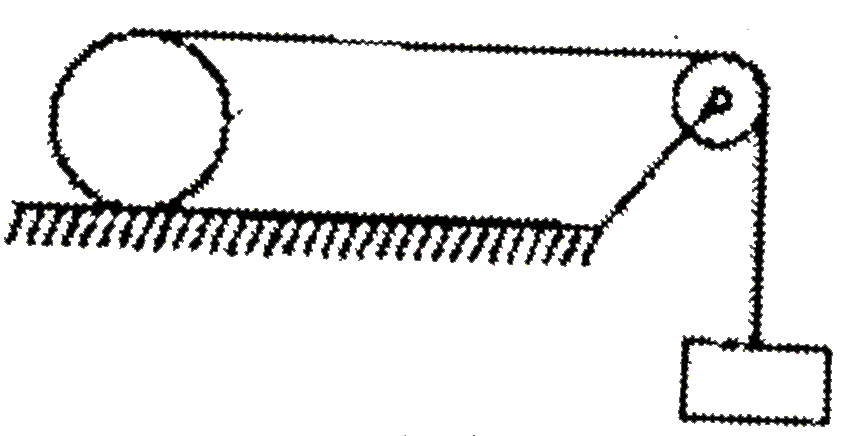
Velocity of hanging block at this moment is: is:
View SolutionA sphere a ring and a disc of same mass and radius are allowed to roll down three similar sufficiently rough inclined planes as shown in the figure from same height.
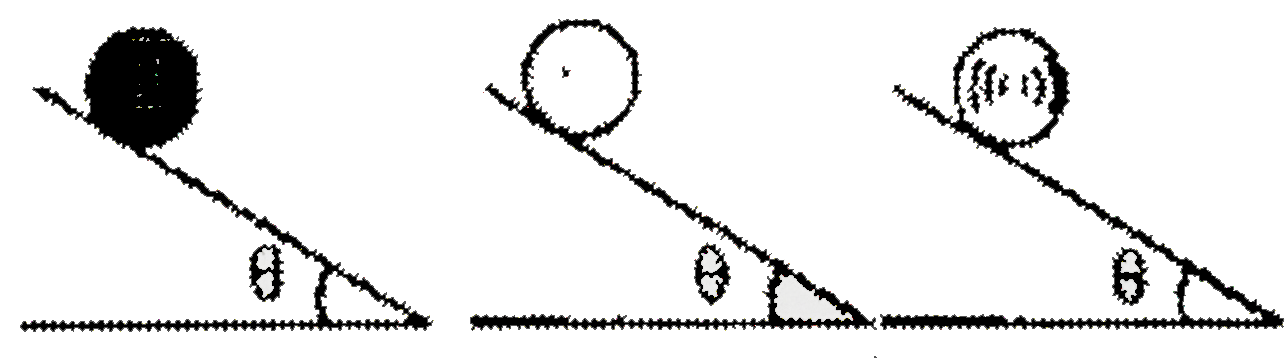
Which of the follwing order is true for final `KE` of the bodies?
View SolutionA sphere a ring and a disc of same mass and radius are allowed to roll down three similar sufficiently rough inclined planes as shown in the figure from same height.
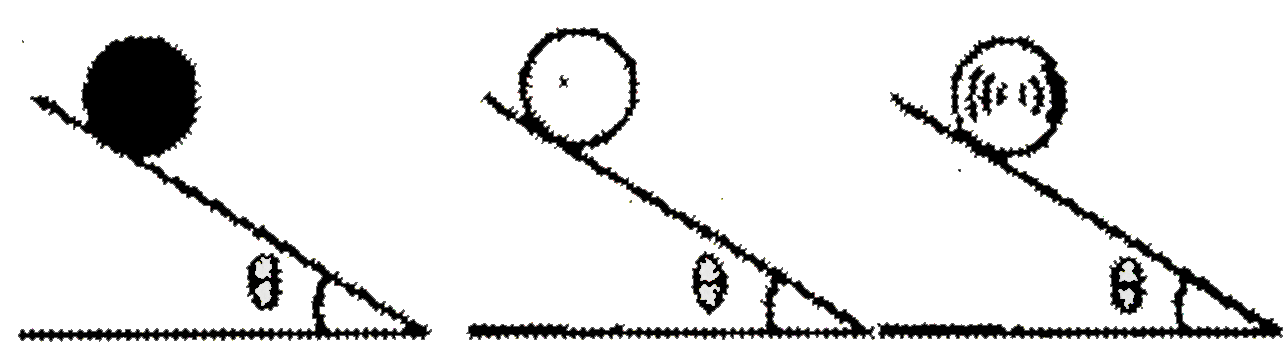
Which of the following order is true for final linear velocity of the bodies?
View SolutionA sphere a ring and a disc of same mass and radius are allowed to roll down three similar sufficiently rough inclined planes as shown in the figure from same height.

Which of the following order is' true for tiine taken by the bodies to reach the bottom of incline?
View SolutionA sphere a ring and a disc of same mass and radius are allowed to roll down three similar sufficiently rough inclined planes as shown in the figure from same height.
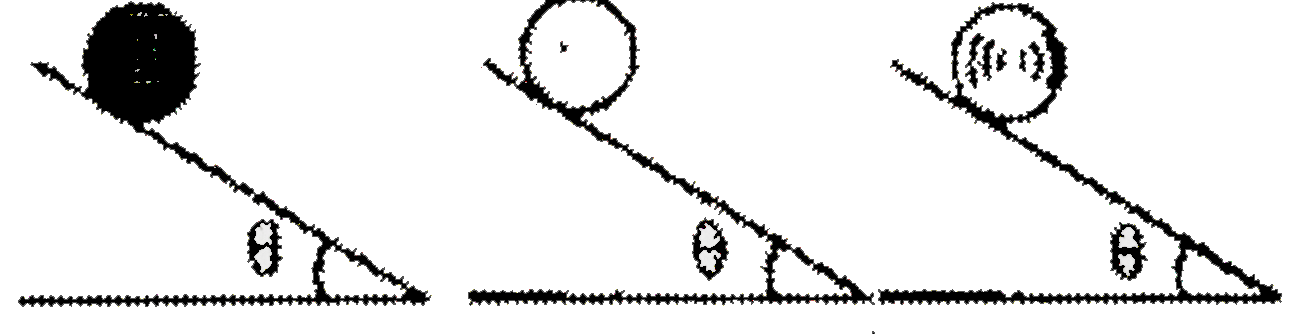
Which of the following order is true for frjctional force acting on the bodies during their rolling?
View SolutionTwo discs `A` and `B` are mounted coaxially ona vertical axle. The discs have moments of inertia `l` and `2l` respectively about the common axis. Disc A is imparted an initial angular velocity `2 omega` using the centre potential energy of a spring compressed by a distance `x_(1)`. Disc `B` is imparted angular velocity `omega` by a spring having the same spring constant and compressed by a distance `x_(2)`. Both the disc rotate in the clockwise direction.
The rotation `x_(1)//(x_(2)` is.
View SolutionTwo discs A and B are mounted coaxiallay on a vertical axle. The discs have moments of inertia I and 2 I respectively about the common axis. Disc A is imparted an initial angular velocity `2 omega` using the entire potential energy of a spring compressed by a distance `x_1` Disc B is imparted an angular velocity `omega` by a spring having the same spring constant and compressed by a distance `x_2` Both the discs rotate in the clockwise direction.
When disc B is brought in contact with disc A, they acquire a common angular velocity in time t. The average frictional torque on one disc by the other during this period is
View SolutionTwo discs `A` and `B` are mounted coaxially ona vertical axle. The discs have moments of inertia `l` and `2l` respectively about the common axis. Disc A is imparted an initial angular velocity `2 omega` using the centre potential energy of a spring compressed by a distance `x_(1)`. Disc `B` is imparted angular velocity `omega` by a spring having the same spring constant and compressed by a distance `x_(2)`. Both the disc rotate in the clockwise direction.
The loss of kinetic energy the above process is -
View SolutionTwo discs `A` and `B` are mounted coaxially on a vertical axle. The discs have moments of inertia `I` and `2I` respectively about the common axis. Disc `A` is imparted an initial angular velocity `2omega` using the entire potential energy of a spring compressed by a distance `x_(1)`. Disc `B` is imparted an angular velocity `omega` by a spring having the same spring constant and compressed by a distance `x_(2)`. Both the discs rotate in the clockwise direction.
A small object of uniform density rolls up a curved surface with an initial velocitiy `v`. It reaches upto a maximum height of `(3v^(2))/(4g)` with respect to the initial position. The object is:
View Solution
COMPREHENSION_TYPE questions and complete solutions for chapter RIGID BODY MOTION of SHREE BALAJI PHYSICS (HINGLISH) of Class 11