Complete Solutions to MCQ_TYPE of chapter RIGID BODY MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | RIGID BODY MOTION |
| ANURAG MISHRA | MCQ_TYPE |
| Number Of Questions | 41 |
| Academic Year | 2023-24 |
A ring mass `m` and radius `R` has three particle attached to the ring as shown in the figure. The centre of the centre `v_(0)`. Find the kinetic energy of the system. (Slipping is absent).
 .
.
View SolutionA block of mass `m` moves on a horizontal rough surface with initial velocity `v`. The height of the centre of mass of the block is `h` from the surface. Consider a point `A` on the surface.
View SolutionA uniform circular disc of radius `r` . 1placed on a rough horizontal plane has initial velocity `v_(0)` and an angular velocity `omega_(0)` as shown. The disc comes to rest after moving some distance in the direction of motion. Then
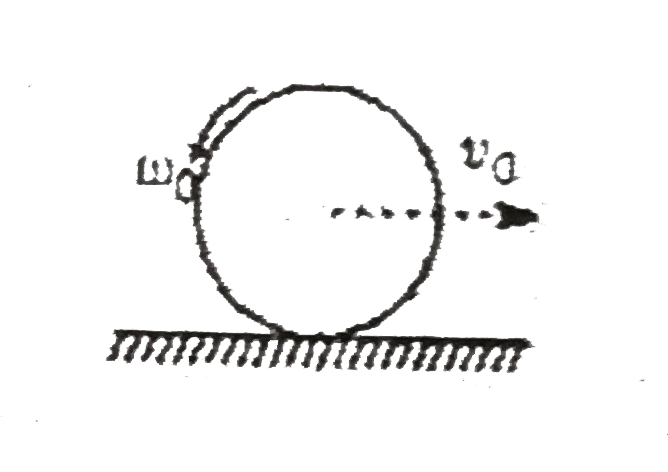
View SolutionA non-uniform ball of radius R and radius of gyration about geometric centre `=R//2` is kept on a frictionless surface. The geometric centre coincides with the centre of mass. The ball is struck horizontally with a sharp impulse `=J` the point of application of the impulse is at a height `h` above the surface. then.
View SolutionTwo equal uniform rods P and Q move with the same velocity v as shown in the figure. The second rod has an angular velocity `omega(lt 6v//l)` (clockwise) about G in addition to v.
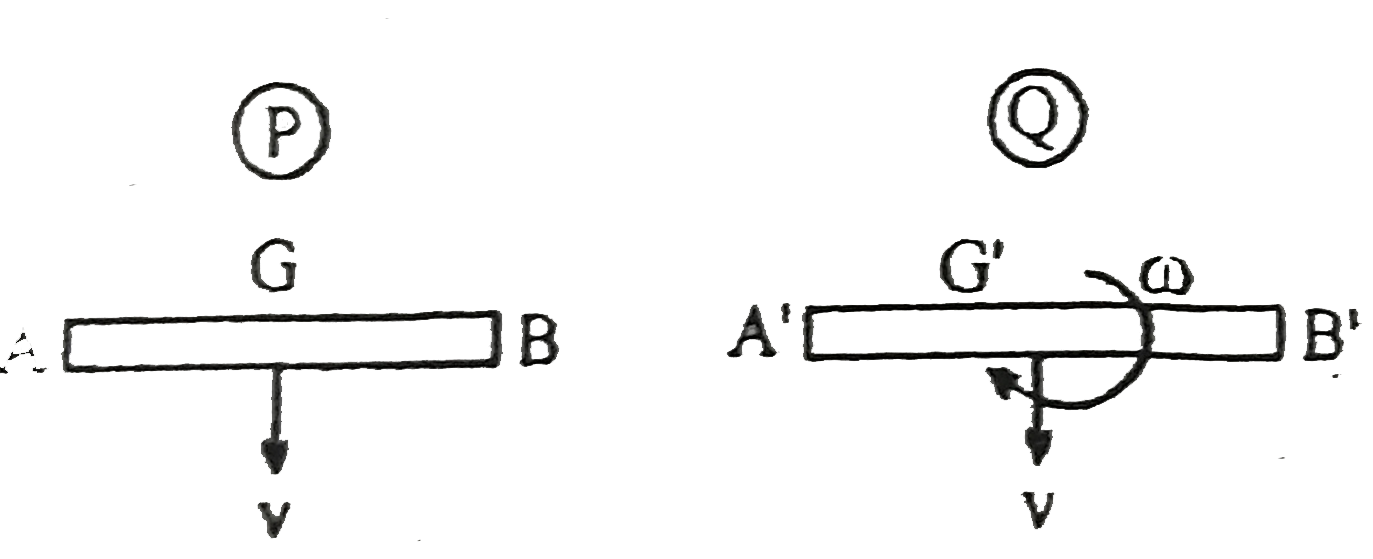
View SolutionA thin uniform rod of mass `m` and length `L` rotates with the constant angular velocity `omega` about .the vertical axis passing through the rod's suspensjon point `O`. It describes a carried surface, then:
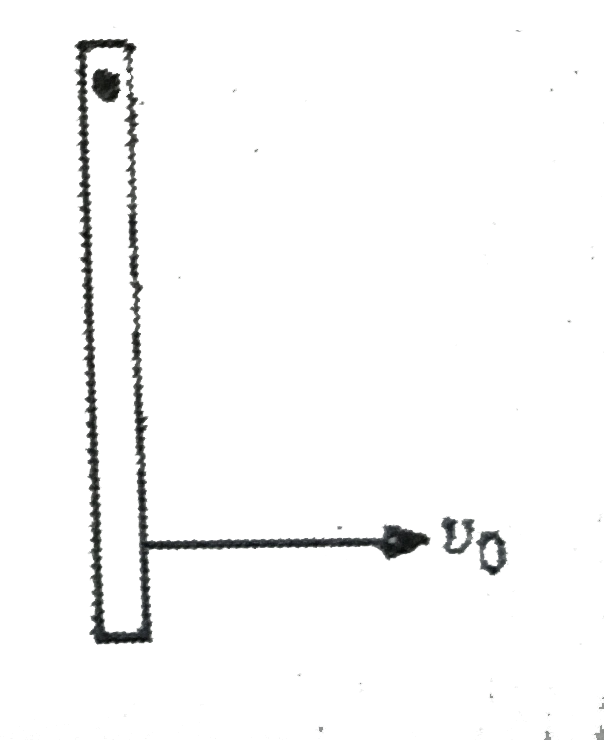
View SolutionA thin uniform rigid rod of length `l` is hinged at one end so that it can move ina vertical plane by rotating about a horizontal axis through upper end. The lower end is given a sharp blow and made to acquire a linear velocity Maximum height attained by lower end of the rod is:
View SolutionA cylinder is rotated clockwise and lowered slowly on arough inclined plane with `(mu=0.8)`. Then:

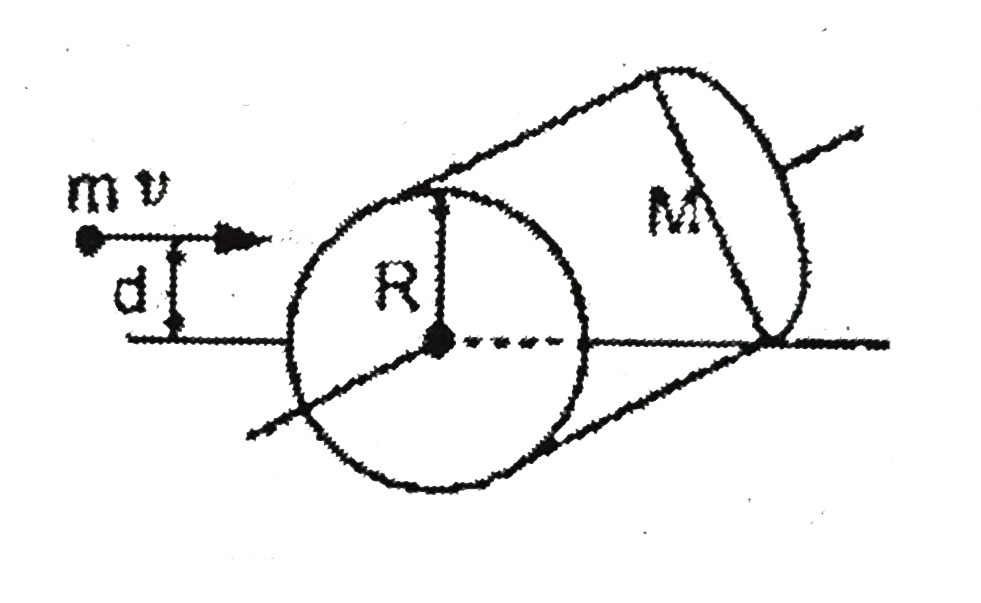
View SolutionA wad of sticky clay of mass `m` and velocity `v_(i)` is fired at a solid cylider of mass `M` and radius `R` figure. The cylinder is initially at rest and is mounted on a fixed horizontal axle that runs through the centre of mass. The line of motion of the projectile is perpendicular to the axle and at a distance `d`, less thant `R`, from the centre
View SolutionA uniform circular disc of radius `R` lies in the `XY` plane with its centre coinciding with the origin.The moment of inertia about an axis passing through a point on the X-axis at a distance `x=2R` and perpendicular to the X-Y plane is equal to its moment of inertia about an axis passing through a point on the Y-axis at a distance `y=d` and parallel to the X-axis in the X-Y plane. The value of `d` is
View SolutionA uniform disc of mass `M` and radius `R` is pivoted about a horizontal axis passing through its edge. It is released from rest with its centre of mass at the same height as the pivot.
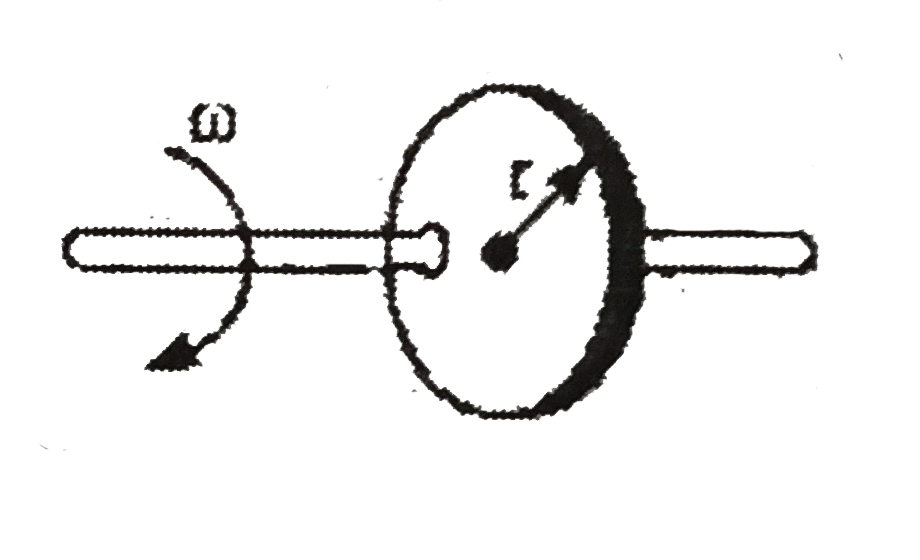
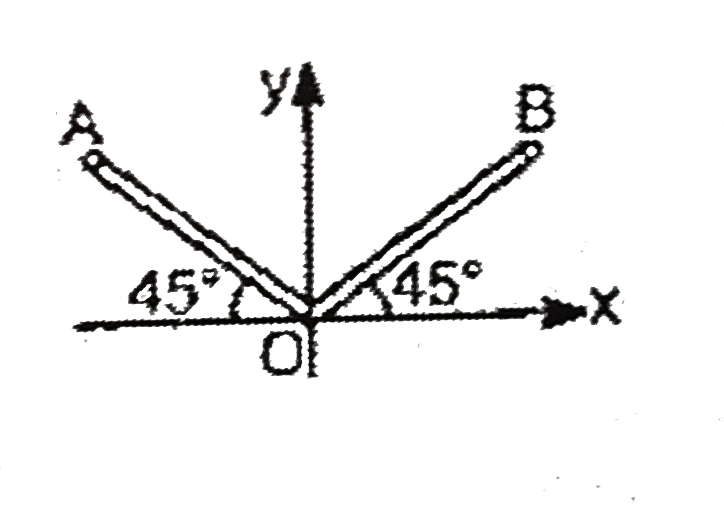
View SolutionTwo rods `OA` and `OB` of equal length and mass are lying on `xy` plane as shown in figure. Let `I_(x),I_(y)` & `I_(z)` be the moment of inertias of both the rods abour `x,y` and `z` axis respectively. Then:
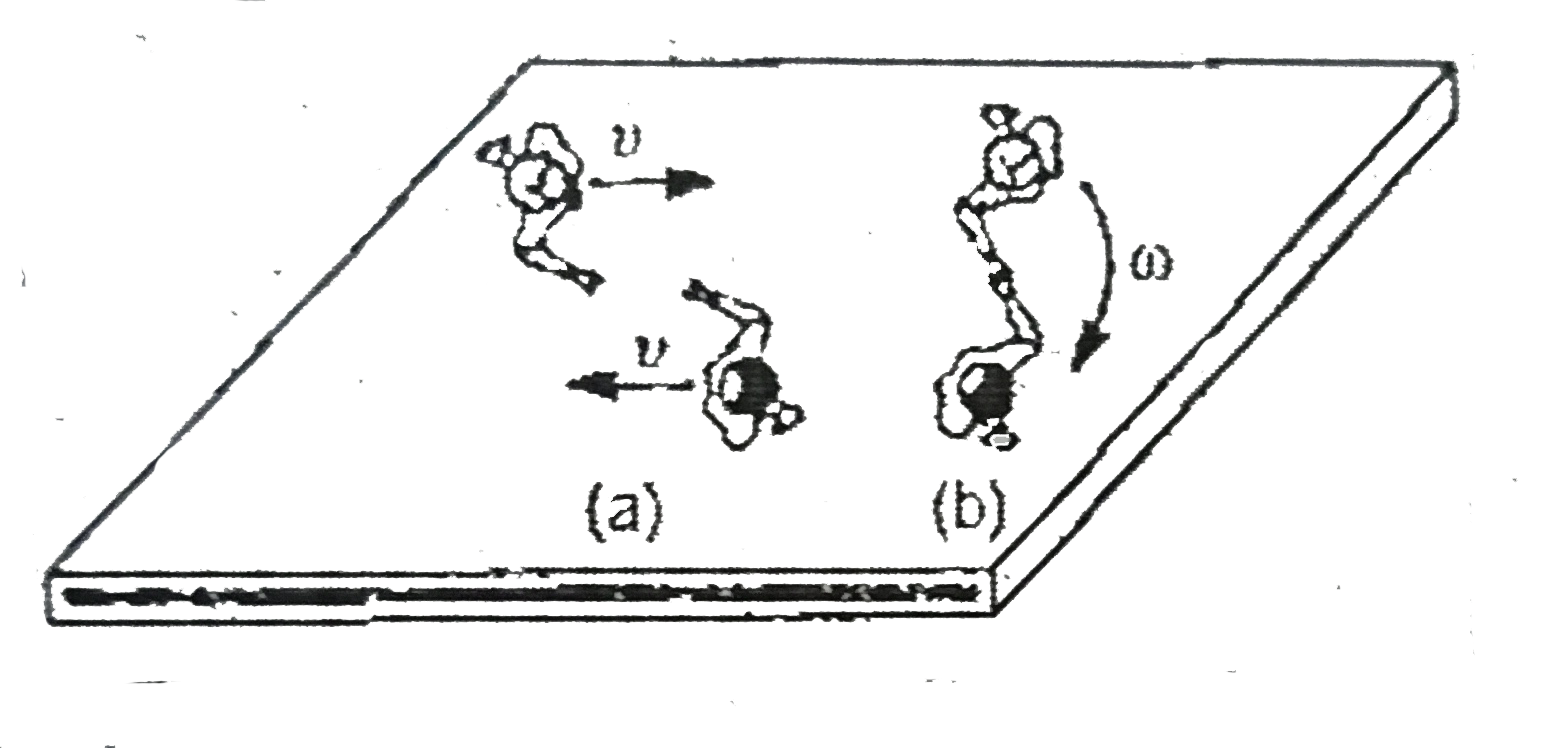
View SolutionTwo skaters approach each other as shown in figure and lock hans. Given each has an initial speed of `2.50m//s` relative to ice. Each has a mass of `70.0kg` and their centres of mass are `0.800m` from their locked hands. You may approximate their momerits of inertia to be that of point masses at this radius:
View SolutionA wire of length `l` and mass `m` is first bent in a circle, then in a square and then in an equilateral triangle. The moment of inertia in these three cases about an axis perpendicular to their planes and passig through their centres of mass are `I_(1),I_(2)` & `I_(3)` respectively. Then maximum of them is:
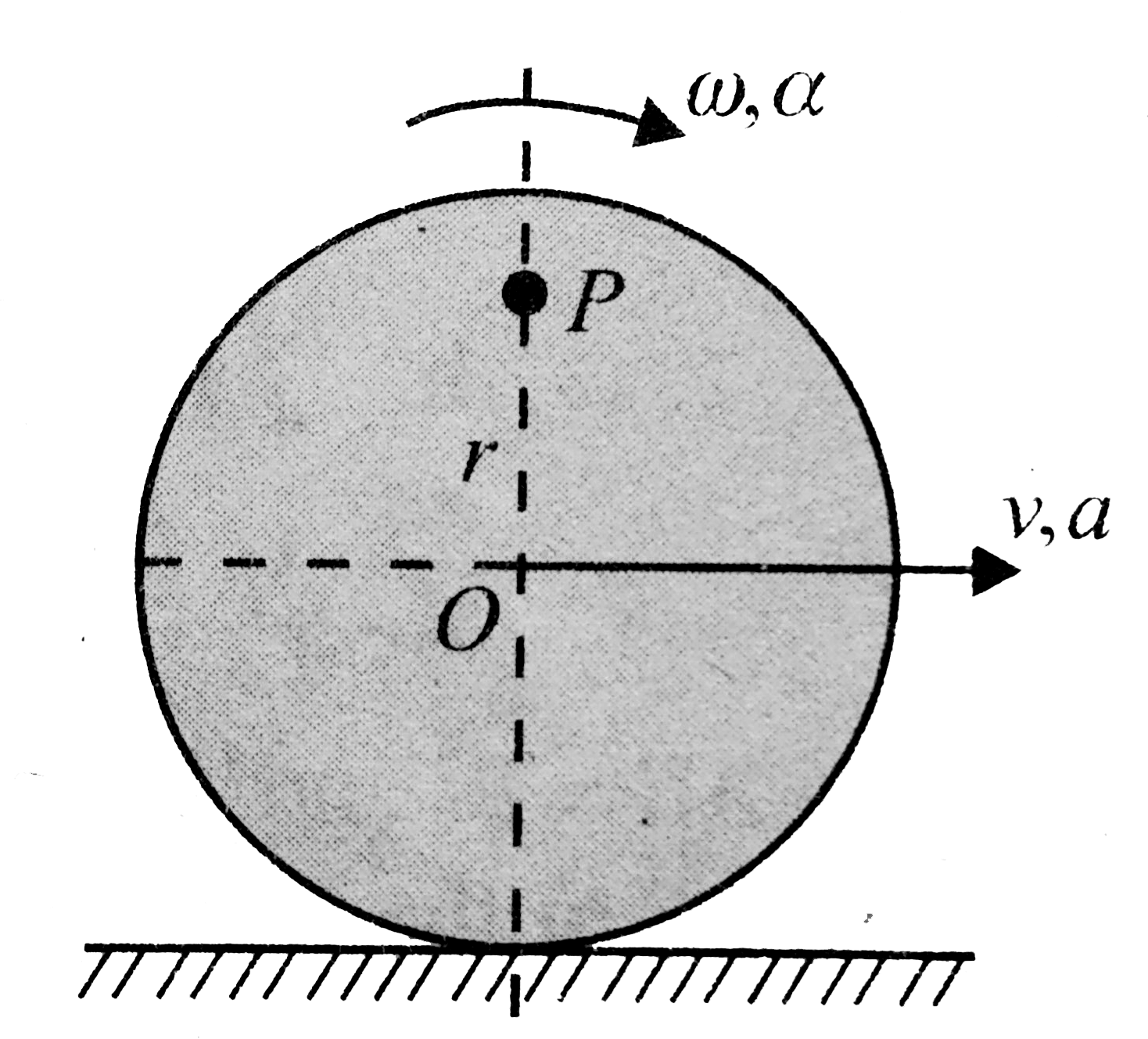
View SolutionA disc of radius `R` rolls on a horizontal ground with linear acceleration `a` and angular acceleration `alpha` as shown in Fig. The magnitude of acceleration of point `P` as shown in the figure at an instant when its linear velocity is `v` and angular velocity is `omega` will be a
View SolutionA block with a square base measuring axa and height `h`, is placed on an inclined place. The coefficient of friction is `m`. The angle of inclination `(theta)` of the plane is gradually increased. The block will.
View SolutionA sphere is projected npon a rough inclined plane. The friction coefficient between the solid sphere and the incline is`mu`. The centre of the sphere is given an initial upward' velocity at `t=0` without imparting any initial angular velocity. Then, which of the following statement (s) is/are true?
View SolutionA uniform rod of length `l` and mass `2m` rests on a smooth horizontal table. A point of mass `m` moving horizontally at right angle to the rod with velocity `v` collides with one end of the rod and sticks to it, then:
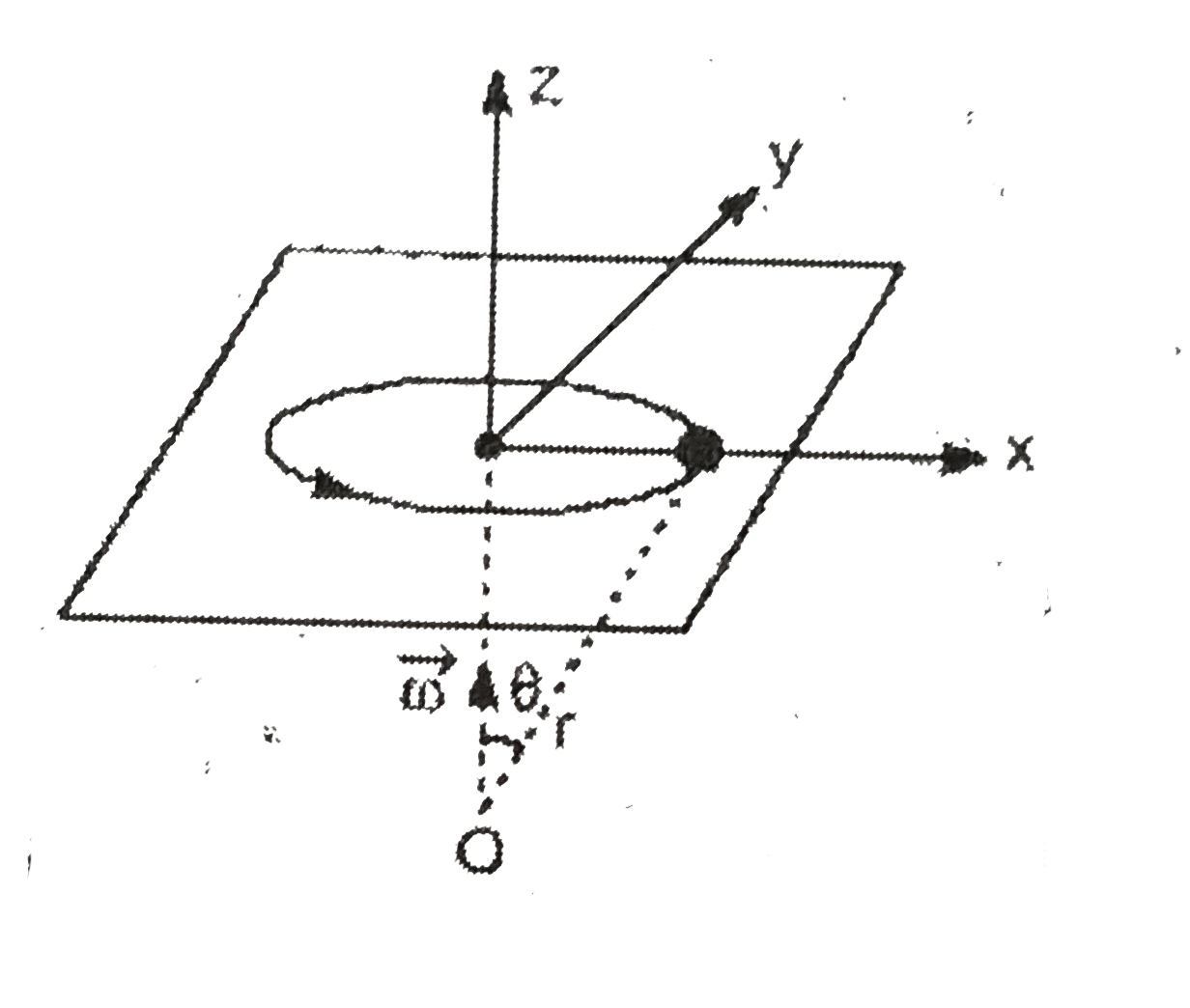
View SolutionA mass `m` is attached to a rigid rod of negligible mass as shown in figure. The system is pivoted at point `O` and rotates about the indicated `z`-axis with angular velocity `vec(omega)`, maintaining a fixed angle `theta` with the axis.
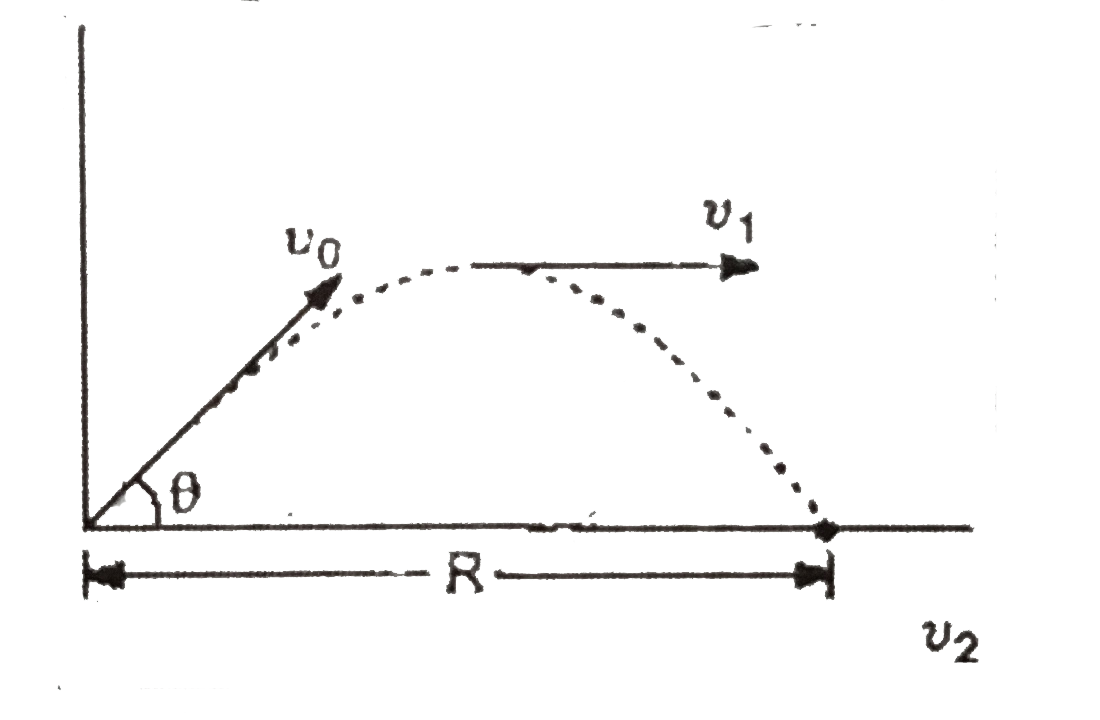
View SolutionA projectile is projected with a velocity`v_(0)` at an angle ` theta` with the horizontal as shown in figure. The angular momentum of particle about the origin:
View SolutionA woman of mass `m` stands at the edge of ,a solid cylindrical platform of mass `M` and radius `R`. At `t = 0` the platform is rotating with negligible friction at angular velocity `omega_(0)` about a vertical axis passing through the centre. The woman begins to walk with speed `v`, relative to the platform, towards the centre of the platform:
View SolutionA solid cube of side `2a` and mass `M`, sliding on a smooth surface with velocity `v_(0)` , collides inelastically with the raised edge of the table:
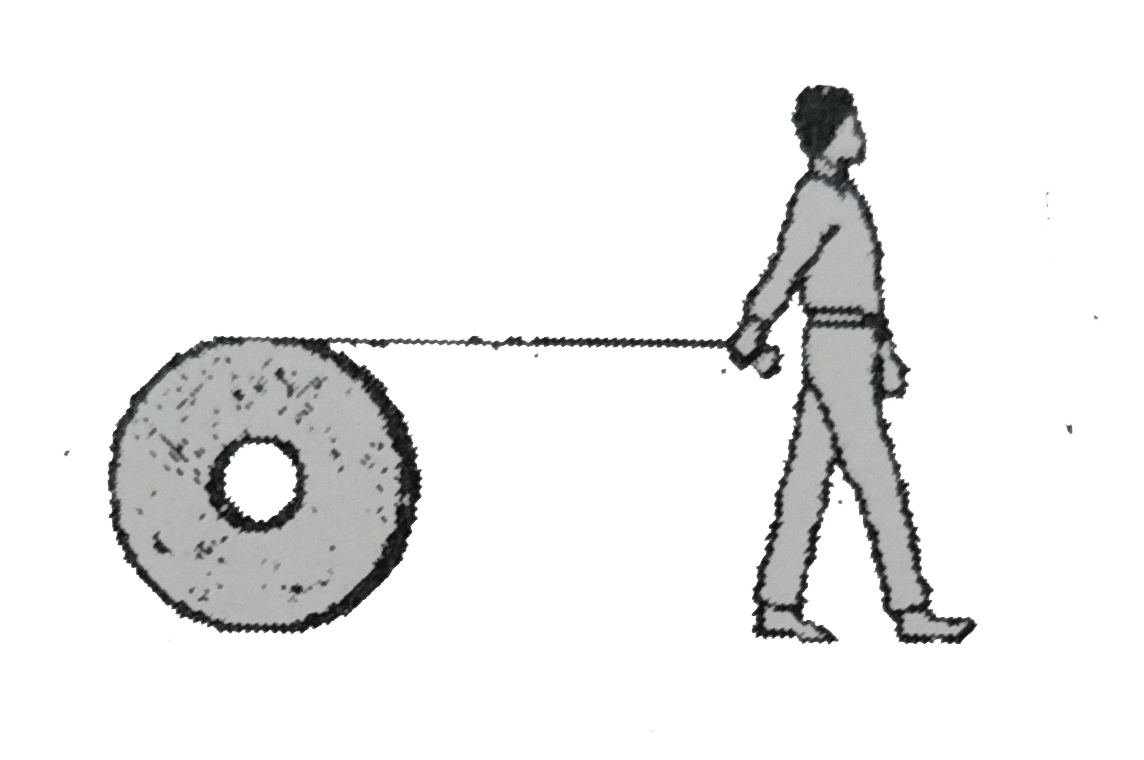
View SolutionA large spool of rope stands on the ground with the end of the rope lying on the top edge of the spool. A person grabs the end of the rope and walks a distance, holding onto it figure. The spool rolls behind the person without slipping. What is the length of rope that unwinds from the spool? How far does the spool's CM move?
View SolutionA constant power is suppied to a rotating disc. The relationship between the angular velocity `(omega)` of the disc and number of rotations `(n)` made by the disc is governed by
View SolutionA force `F` is applied on the top of a cube as shown in the figure. The coefficient of friction between the cube and the ground is `mu`. If `F` is gradually increased, find the value of `mu` for which the cube will topple before sliding.
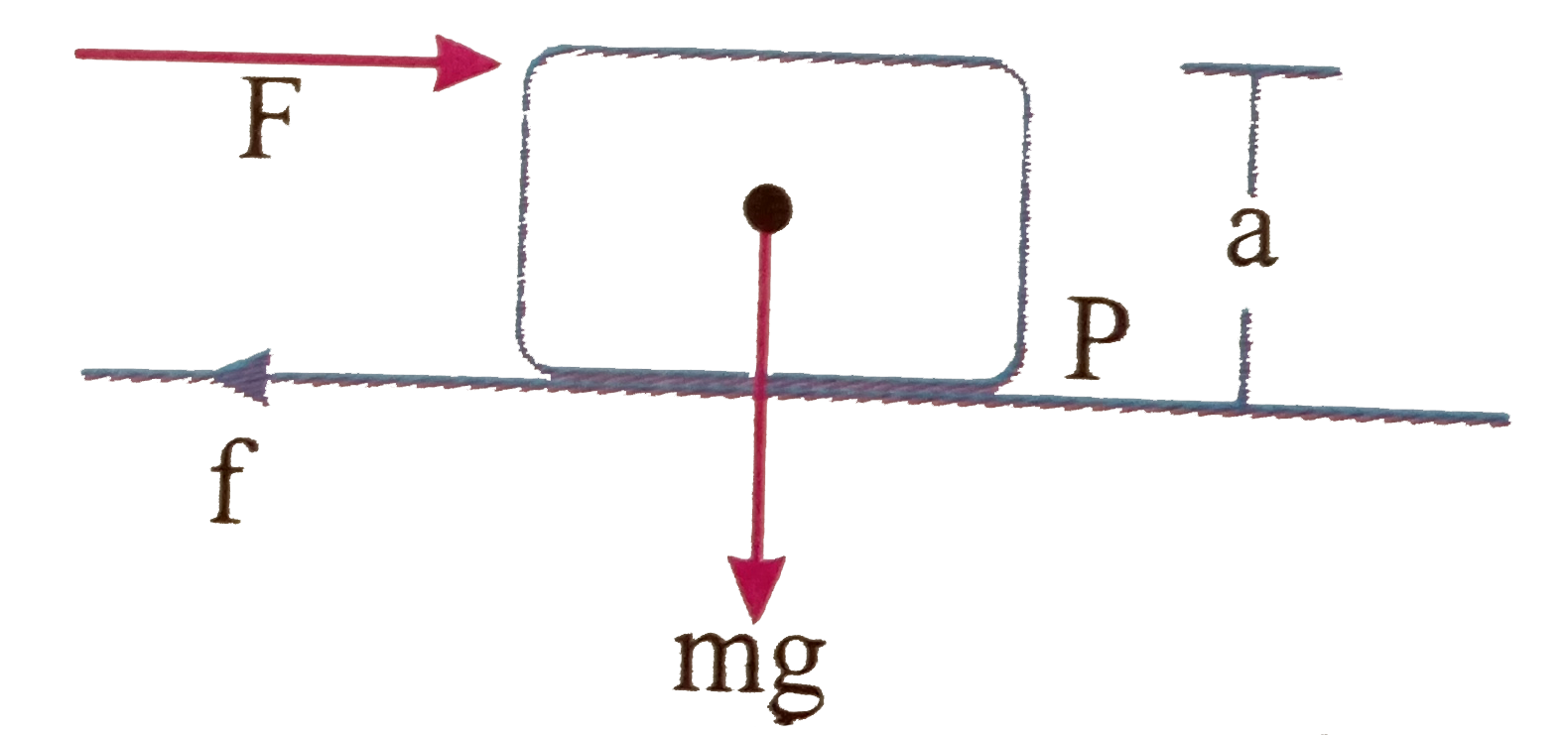
View SolutionA uniform rod `AB` of mass `m` and length `l` is at rest on a smooth horizontal surface. An impulse `J` is applied to the end `B`, perpendicular to the rod in the horizontal direction. Speed of particlem `P` at a distance `(l)/(6)` from the centre towards `A` of the rod after time `t = (pi m l)/(12 J)` is.
View SolutionA rod `AB` of length `1m` is placed at the edge for a smooth table as shown in figure. It is hit horizontally at point `B`. If the displacement of centre of mass `m` in `1s` is `5sqrt(2)m`. The angular velocity of the rod is `(g=10m//s^(2))`
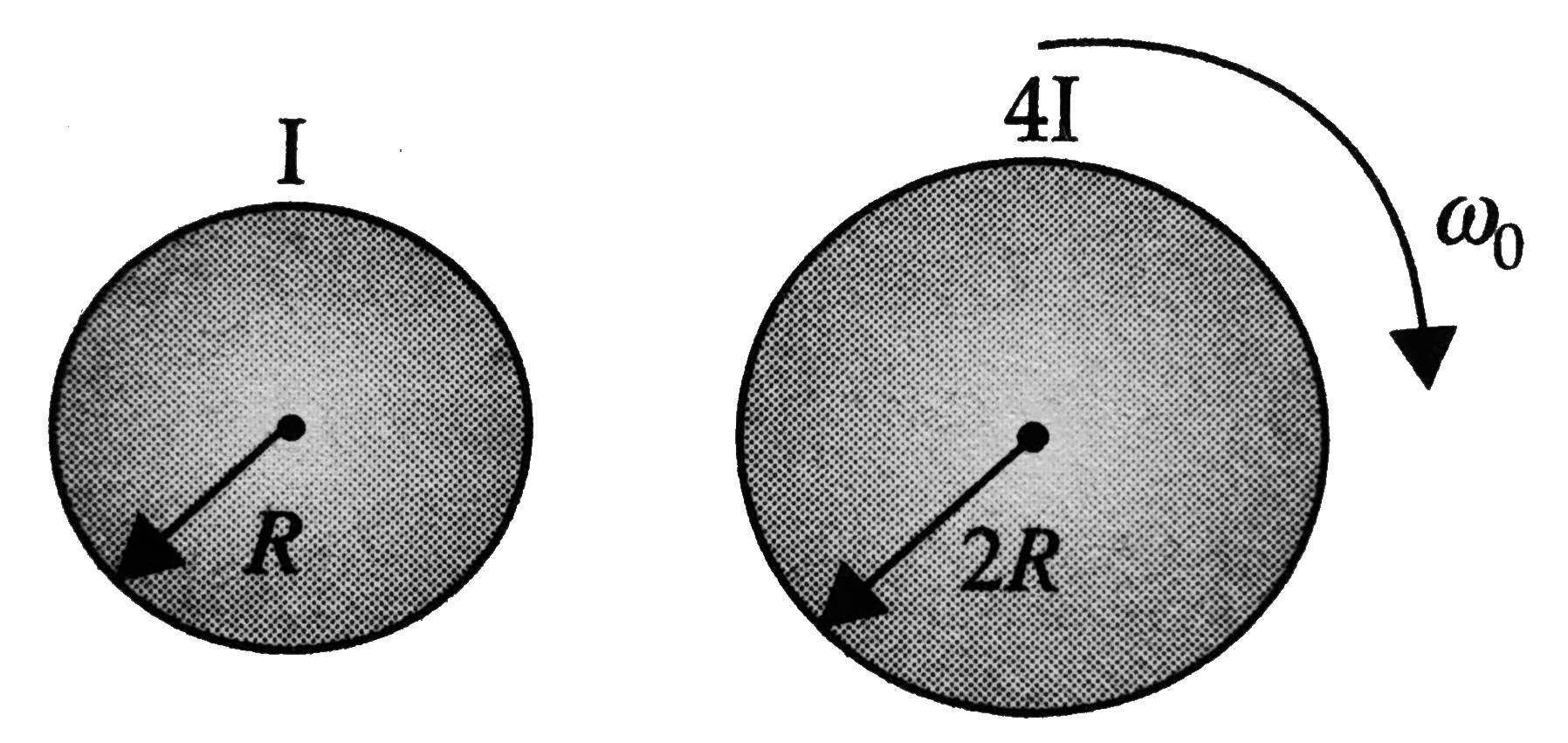
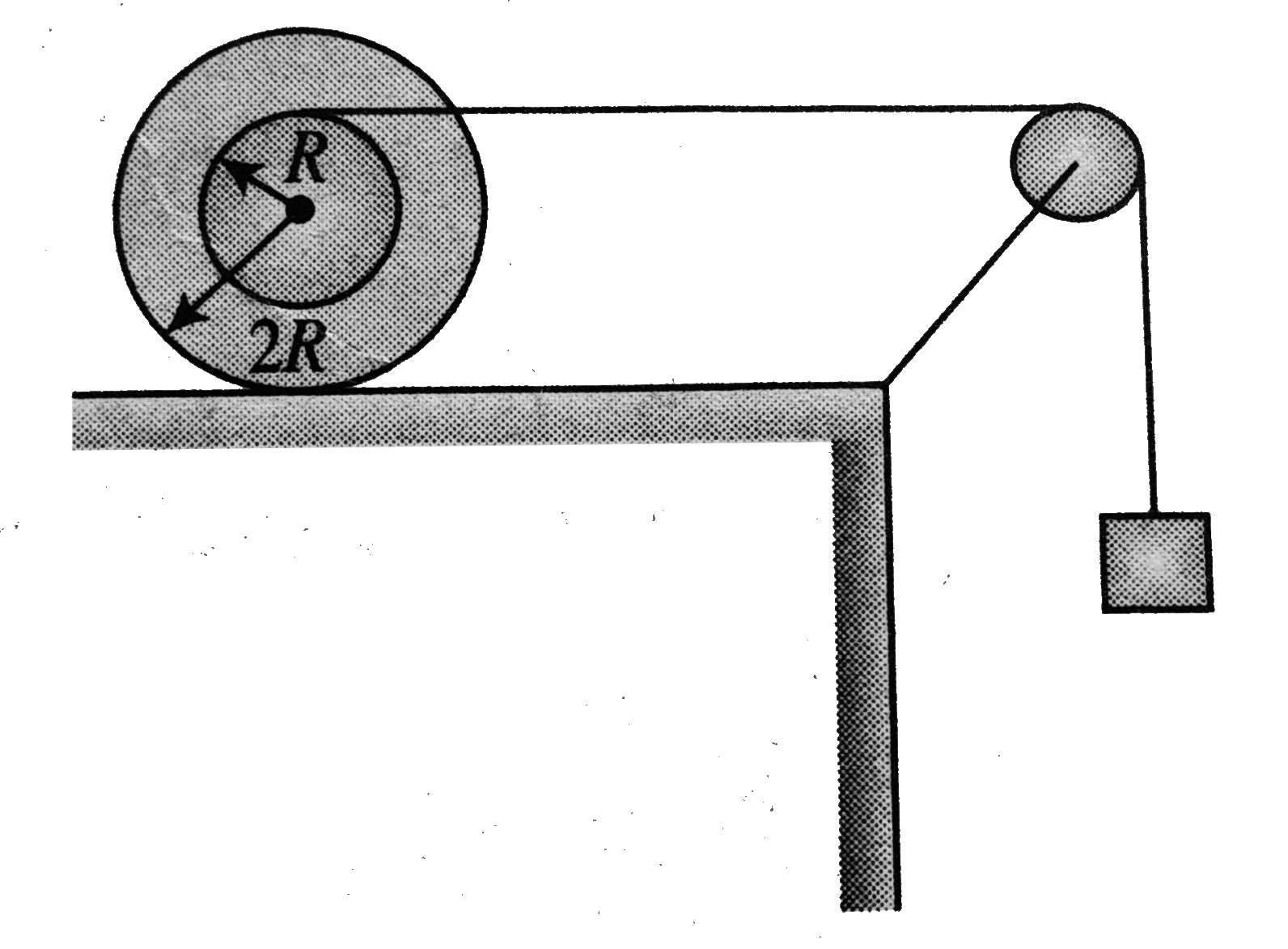
View SolutionTwo cylinders having radii `2R` and `R` and moment of inertia `4I` and `I` about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity `omega_(0)`. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
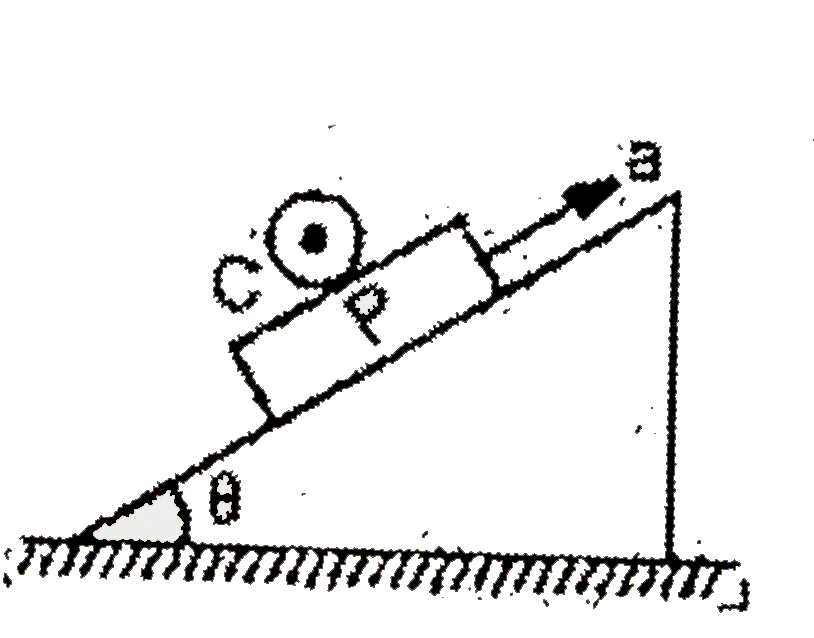
View SolutionThe acceleration `alpha` of the plank `P` required to keep the centre `C` of a cylinder in a fixed position during the motion is (no slipping takes place between cylinder and plank)
View SolutionA rod of mass `m` and length `l` is hinged at one of its end `A` as shown in figure. A force `F` is applied at a distance `x` from `A`. The acceleration of centre of mass (a) variea with `x` as:
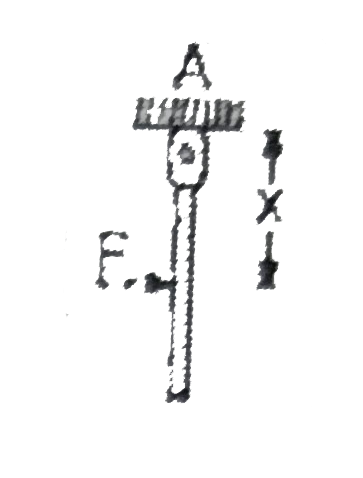
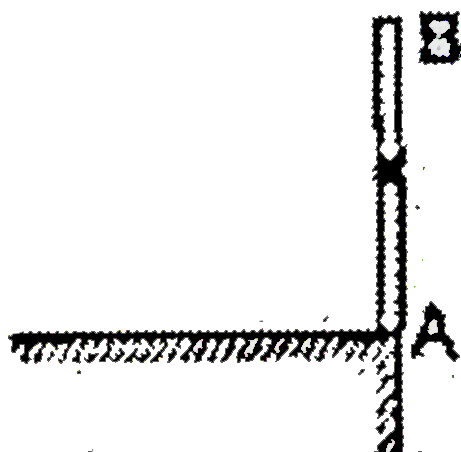
View SolutionA uniform rod of length `l` is pivoted at point `A`. It is struck by a horizontal force which delivers an impulse `J` at a distance `x` from point `A` as shwon in figure, impulse delivered by pivot is zero if `x` is equal to

View SolutionIn the figure shown mass of both, the spherical body and block is `m`. Moment of inertia of the spherical body about centre of mass is `2mR^(2)`. The spherical body rolls on the horizontal surface. There is no slipping at any surfaces in contact. The ratio of kinetic energy of the spherical body to that of block is
View SolutionA particle is projected with velocity `v` at an angle of `theta` with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
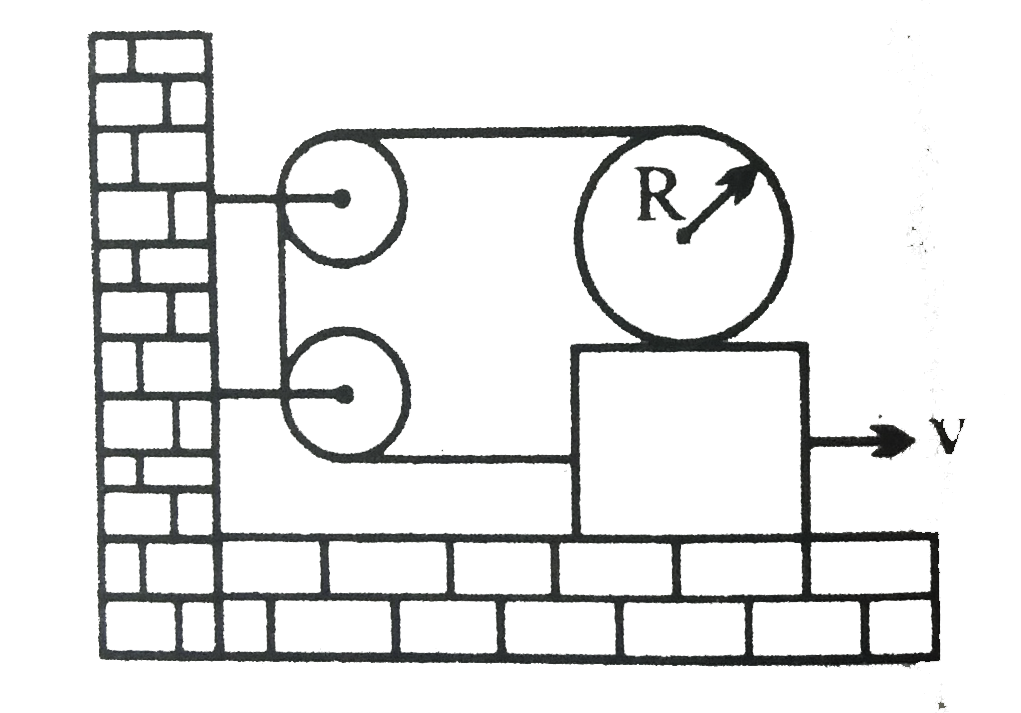
View SolutionIn the figure shown, the plank is being pulled to the right with a constant speed `v`. If the cylinder does not slip then:
 .
.
View SolutionTwo men each of mass `m` stand on the rim of a horizontal circular disc, diametrically opposite to each other. The disc has a mass `M` and is free to rotate about a vertical axis passing through its centre of mass. Each man start simultaneously along the rim clockwise and reaches their original starting points on the disc. The angle turned through by the disc with respect to the ground (in radian) is:
View SolutionA time varying force `F = 2t` is applied on a spool as shown in figure. The angular momentum of the spool at time `t` about bottommost point is:

View SolutionA spherical body of radius `R` rolls on a horizontal surface with linear velociltly `v`. Let `L_(1)` and `L_(2)` be the magnitudes of angular momenta of the body about centre of mass and point of contact `P`. Then:
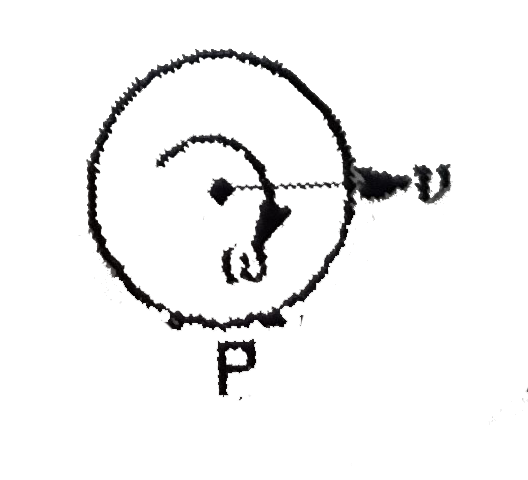
View SolutionA thin uniform rod `AB` of mass `1kg` move translationally with acceleration `a=2m//s^(2)` due to two antiparallel force as shown. If `l=20cm` then:
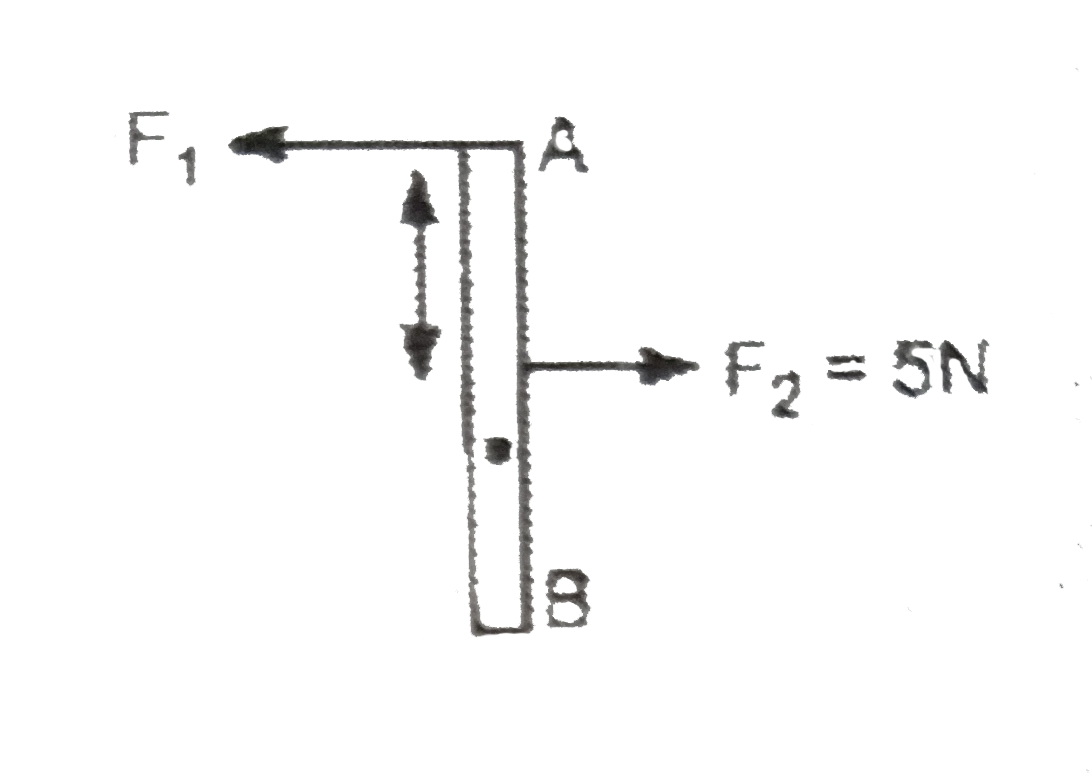
View SolutionThe torque `tau` on a body about a given point is found to be equal to AxxL where A is a constant vector, and L is the angular momentum of the body about that point. From this it follows that
View SolutionA ball moves over a fixed track as shown in the figure. From `A` and `B` the ball rolls without slipping. If surface `B` is frictionless and `K_(A),K_(B)` and `K_(C)` are kinetic energies of the ball at `A,B` and `C` respectively then:
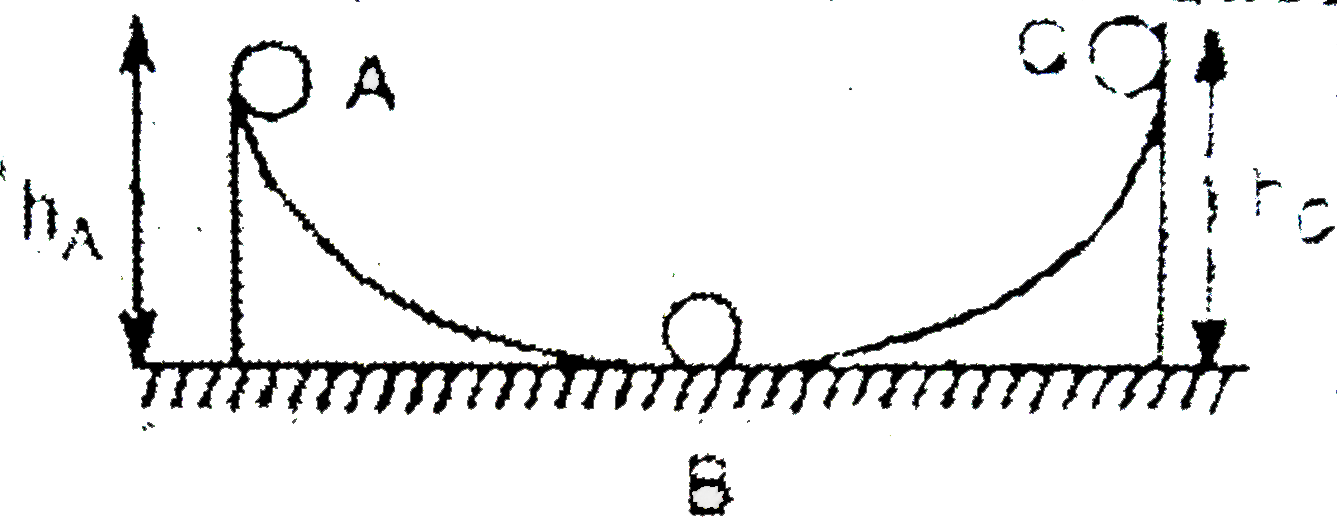
View SolutionA uniform cylinder of mass `M` and radius `R` rolls without slipping down a slope of angle 8 with horizontal. The cylinder is connected to a spring of force constant `k` at the centre, the other side of which is connected to a fixed support at A. The cylinder is released when the spring is unstretched. The· force of friction `(f)`:

View Solution
MCQ_TYPE questions and complete solutions for chapter RIGID BODY MOTION of SHREE BALAJI PHYSICS (HINGLISH) of Class 11