Complete Solutions to EXAMPLE_TYPE of chapter RIGID BODY MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | RIGID BODY MOTION |
| ANURAG MISHRA | EXAMPLE_TYPE |
| Number Of Questions | 52 |
| Academic Year | 2023-24 |
A gyroscope is spinning at angular velocity `omega_(0)`. The power is shut off, and the gyroscope begins to slow down with its angular velocity described by
`omega=omega_(0)e^(-r//T)`
with `T` a constant (a) How long does it take for the gyroscope to reach half its initial angular velocity? (b) What is the gyroscope's initial angular acceleration? (c) What is the gyroscope's average acceleration between the time the power through is cut of and the instant it reaches half speed? (d) Through how many revolutions does the gyroscope turn during this time?
View SolutionFig shows three forces `F_(1), F_(2)` and `F_(3)` acting on a rod pivoted at its end. Find the torque of each force about pivot.
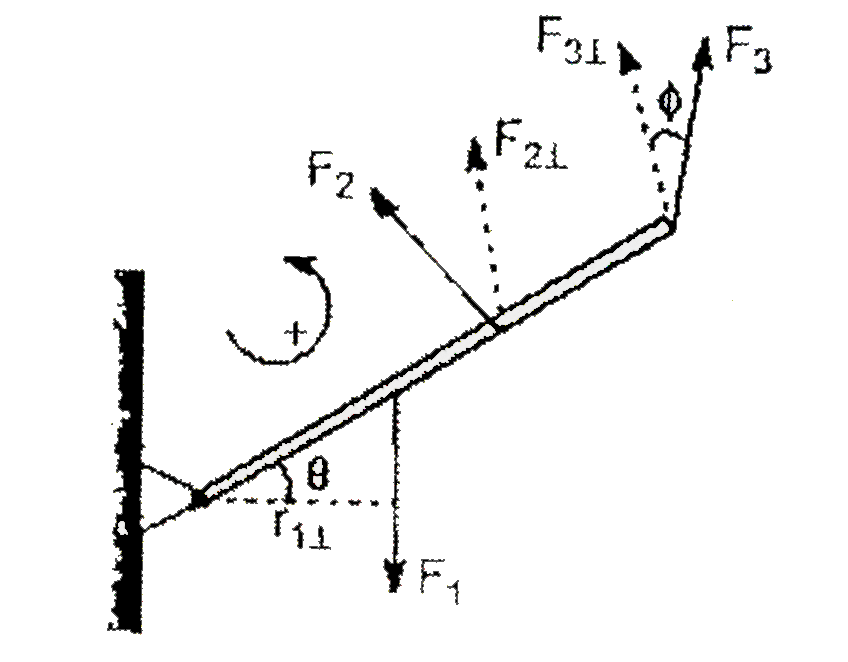
View SolutionFour particles of mass `m` are connected by massless rods to form a rectangle-of sides `2a` and `2b` as shown. The assembly, rotates about an axis in the plane of the figure through the centre. Find the moment of inertia about the axis:,

View SolutionA weighlifter's barbell consists of two heavy discs of mass `m` and radius `R` connected by as light rod of lenth `l gt gt R`. Estimate its moment of inertia about an axis `A` through its `CM` and perpendicular to the rod. Determine its kinetic energy.
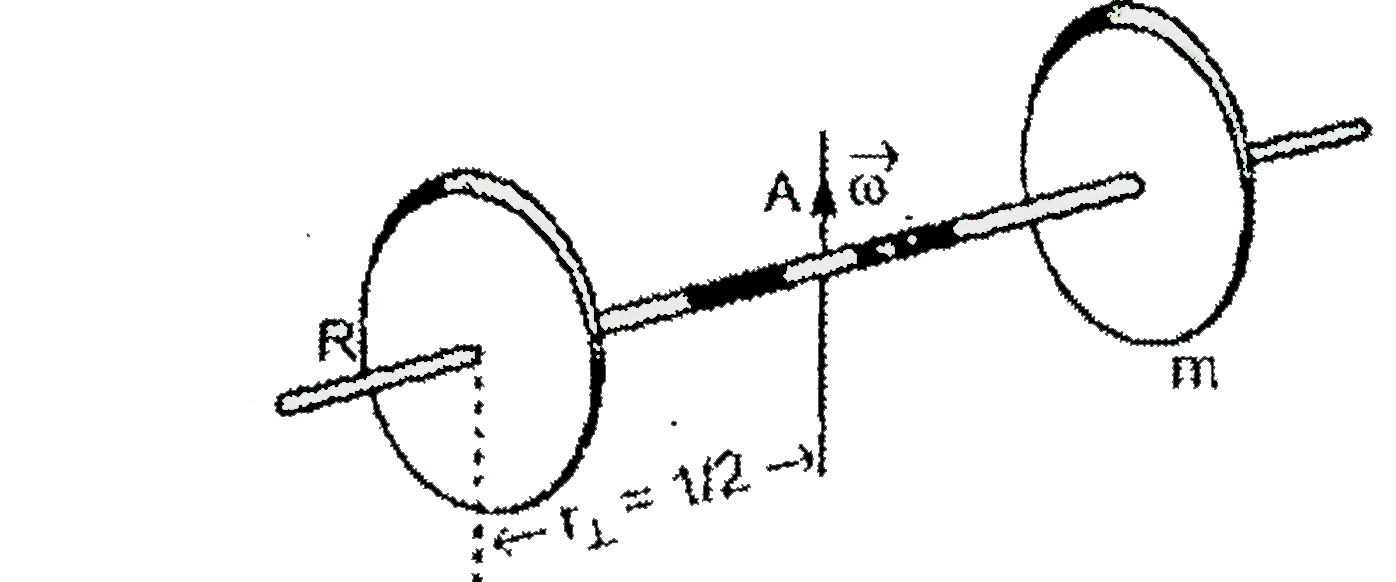
View SolutionCalculate the moment of inertia of a thin rod of mass `m` and length `l` about a symmetry axis through the centre of mass and perpendicular to the length of the rod, as shown in Fig.
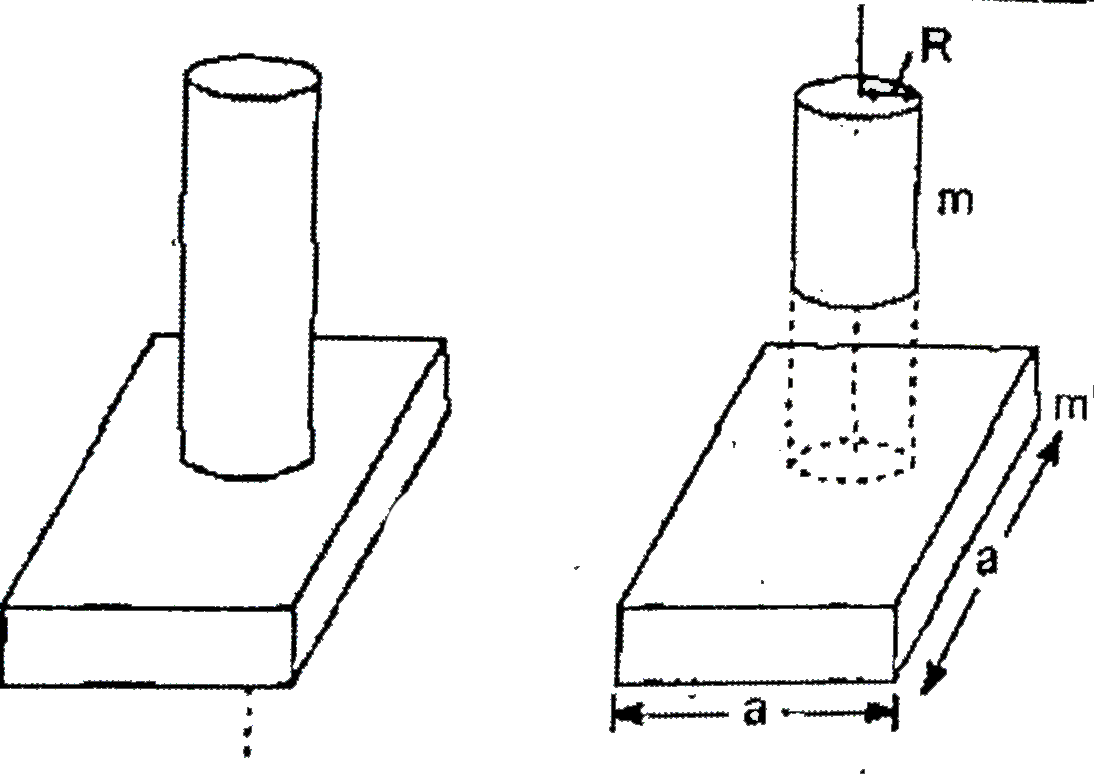
View SolutionA circular hole of radius `r//2` is cut from a circular disc of radius `'r'`. The disc lies in the `xy` plane. Determine the moment of inertia about an axis passing through the centre and perpendicular to the plane of the disc.
View SolutionAn object of mass `m` is tied to a light string wound around a pulley that has a moment of inertia `I` and radius `R`. The wheel bearing is fricrtionless and the string does not slip on the run. Find the tension in the string and the acceleration of the object.
View SolutionTwo blocks are connected by a string that passes over a pulley of radius `R` and moment of inertia `I`. The block of mass `m_(1)` sides on a frictionless, horizontal surface, the block of mass `m_(2)` is suspended from the string. Find the acceleration `a` of the blocks and the tension `T_(1)` and `T_(2)` assuming that the string does not slip on the pulley.

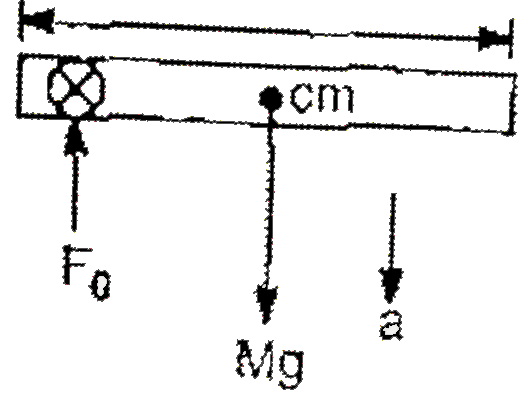
View SolutionA uniform slender rod of length `L` and mass `M` is pivoted at one end. It is held horizontal and releasaed. Assume the pivot is frictionless. Find .
(a) the angular acceleration of the rod immediately after it is released, and
(b) the force `F_(0)` exerted on the rod by the pivot immediately after release.
View SolutionA uniform rod of mass `M` and length `L` with two particles `m` and `m_(2)` attached to its ends, is pivoted at its centre. The system rotates in a vertical plane with angular velocity `omega`.

View SolutionA uniform slender rod of mass `M` and length `L` is pivoted at its end. The rod is released from its nearly vertical position. What is the reaction at the pivot when the rod reaches the horizontal position? If the support is withdrawn at this instant, describe the subsequent motion of the rod.
View SolutionThree particles A, B and C each of mass m, are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side l. This body is placed on a horizonta frictionsess table (x-y plane) and is hinged to it at the point A so that it can move without friction about the vertical axis through A . the body is set into rotational motion on the table about A with a constant angular velocity `omega`.

(a) Find the magnitude of the horizontal force exerted by the hinge on the body.
(b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time T.
View SolutionA uniform rod of length `2a` is placed horizontally on the edge of a table. Initially the centre of mass of the rod is at a distance `a//3` from the edge. The rod is released from rest. If the rod slips after it turned an angle `theta`, find the coefficient of friction between the rod and the table.
View SolutionA uniform board of mass `M` and length `L` rests on two spring scales. A person of mass `m` stands at a distance `l` from one end as shown in Fig. (a) The board and person are at rest. What is the reading of the two scales?
View SolutionA cylinder of weight `W` and radius `R` is to be raised onto a horizontal step of height `h` as shown in Fig. A rope is wrapped around the cylinder and pulled horizontally with force `F`. Assuming the cylinder does not slip on the step, find the minimum force `F` necessary to raise the cylinder.

View SolutionA ladder rests on the floor of a room, leaning agains a wall. If the coefficient of static friction between the ladder the floor is `mu_(f)` and that between ladder and is `mu_(w)`, what is the minimum angle `theta` that the ladder can make with the floor if the ladder is not to slip? Assume that the mass of the ladder is distributed uniformly.

View SolutionA block of height `h` is projected along a rough surface of coefficient of friction `mu`. Find the point of application of the normal force on the block for `mu_(k) = 0.5`.
View SolutionThe block in figure has dimensions `m` by `h` and the ramp is inclined at `theta` to the horizontal. Find the effective point of application of the normal force `vec n`.(consider rotational equilibrium)
View SolutionA car of mass `m` travelling at speed `v` moves on a horizontal track. The centre of mass of the car describes a circle of radius `r`. If `2a` is the separation of the inner and outer wheels and `h` is the height of the centre of mass above the ground, show that the limiting speed beyond which the car will overturn in given by
`v^(2)=(gra)/h`
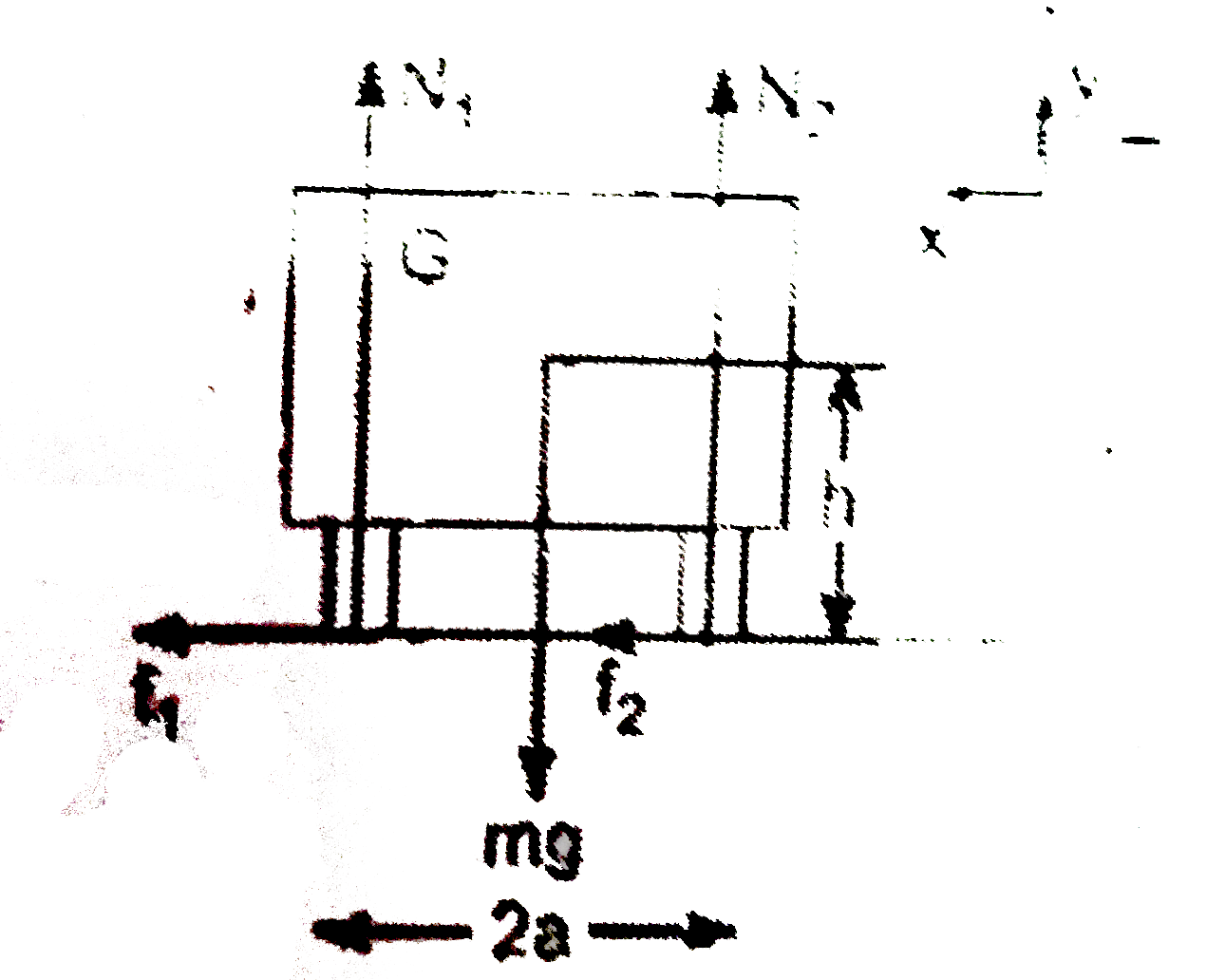
View SolutionA horizontal force `F` is applied to a homogeneous rectangular block of mass `m`, width `b` and height `H`. The block moves with constant velocity, the coefficient of friction is `mu_(k)`.
a. What is the greater height `h` at which the force `F` can be applied so that the block will slide without tipping over ?
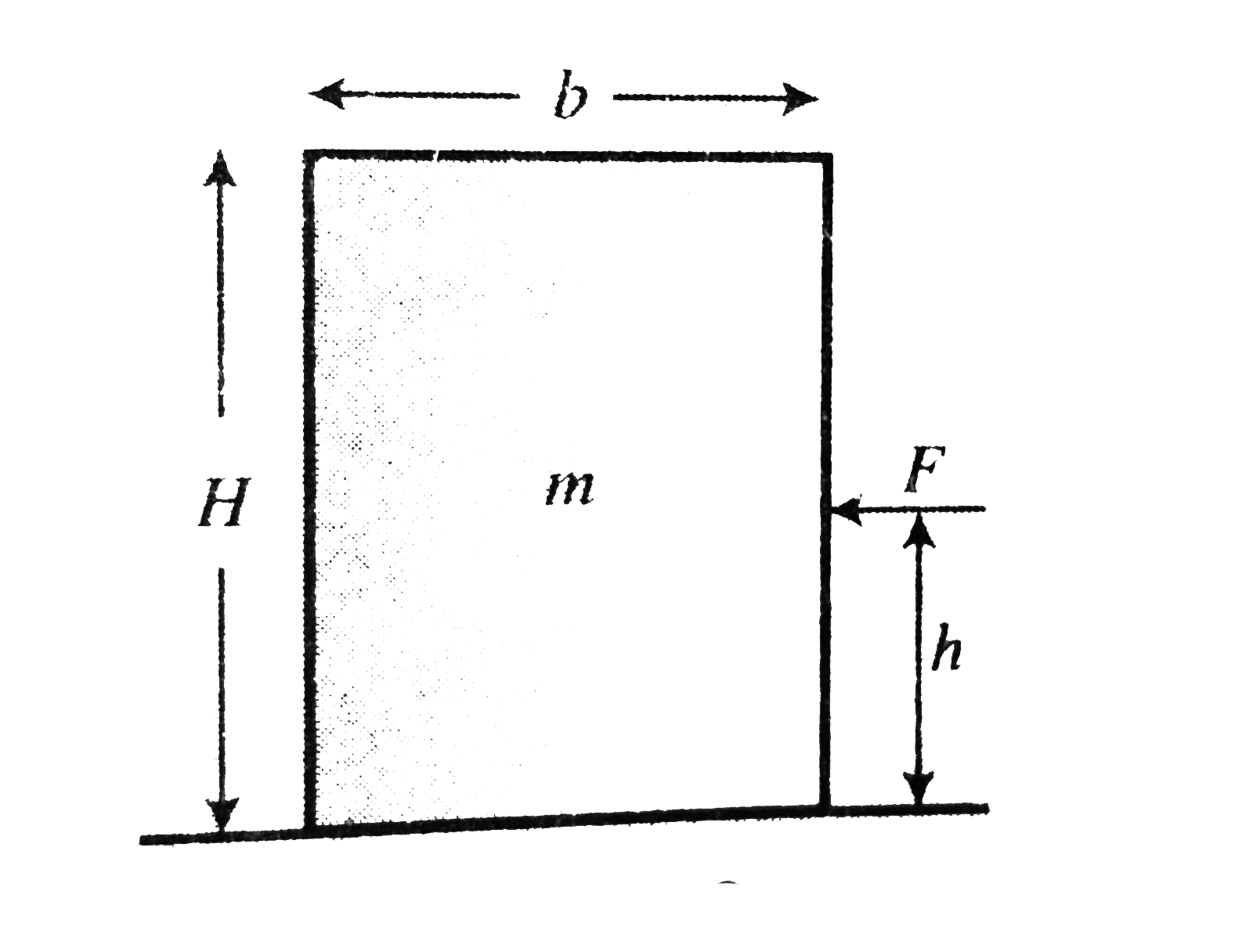
b. Through which point on the bottom face of the block will the resultant of the friction and normal forces act if `h=H//2?`
c. If the block is at rest and coefficient of static friction is `mu_(s)` what are the various criteria for which sliding or tipping occurs?
View SolutionA baggage cart of weight `w` rests on a wall of height `h`. Its centre of gravity is at a distance `L` from the wheel as shown in fig.

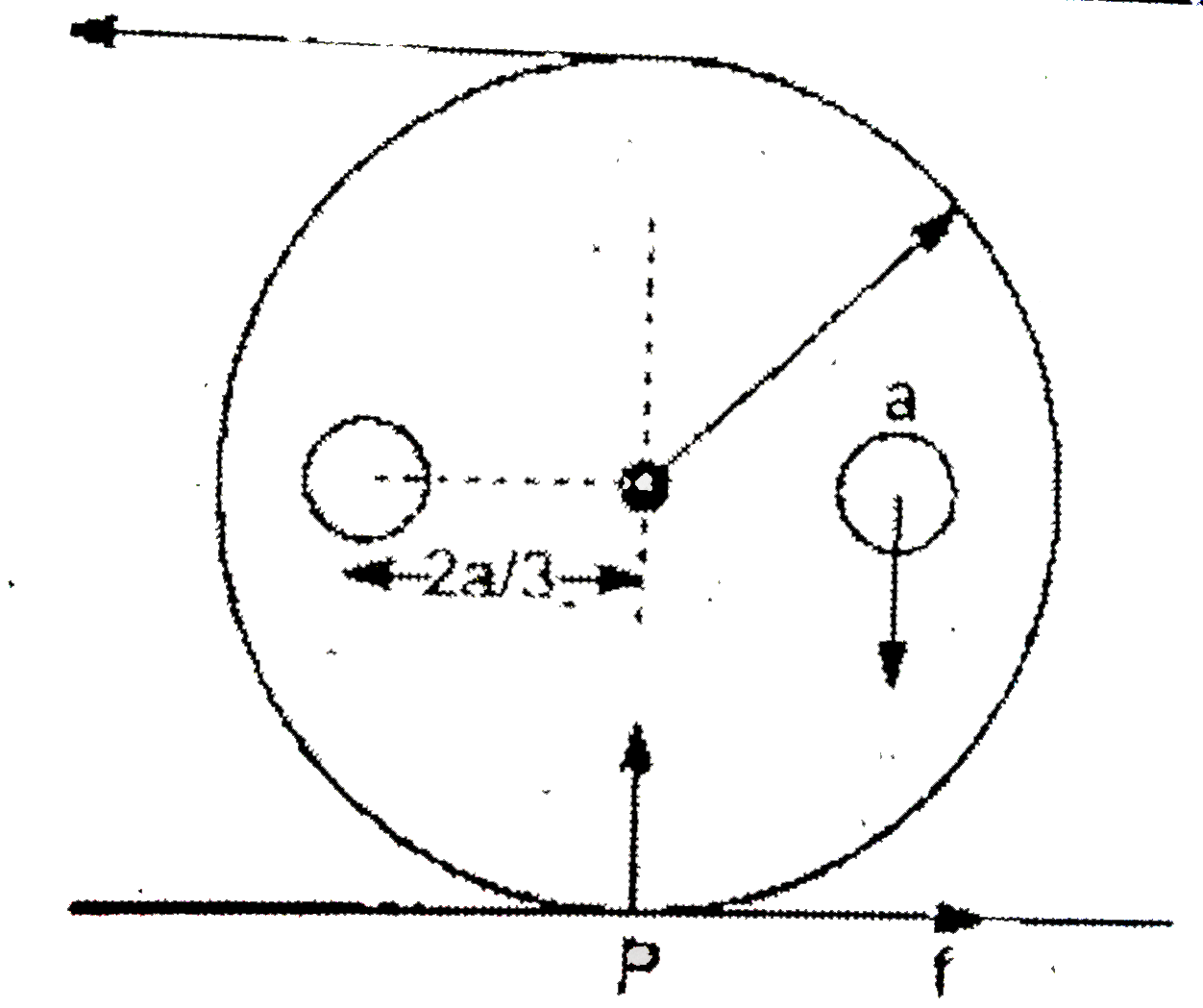
View SolutionFig shows a uniform cylinder of radius a weight `75N`. After on off axis cylindrical hole was drilled through it as shown, it weighed `60N`. The axes of the two cylinders are parallel. Assuming the cyliner does not slip on the table, determine what the tension `T` in the cord must be to keep it from moving.
View SolutionA light ladder rests onn te rough floor of a room, leaning against a smooth wall. The ladder touches the wall at height `h` above the floor. A man climbs up the ladder until the base of the ladder is on the verge of slipping. The coefficint of static friction between the foot of the ladder and floor is `mu`.
(a) What is the horizontal distance moved by the man?
(b) Solve part (a) if the ladder is uniform and has the same weight as the man and the base of the ladder is at a distance `l` from the wall.
View SolutionThe drum of a winch has mass `M` and radius `R`. A cable wound aroung the drum suspends a load of mass `m`. The entire cable has a length `L` and mass per unit length `lamda`, with a total mass `m_(c)=L lamda`. The load begins to fall all toward the ground, unwinding the cable as it goes. How fast is the load moving after it has falled a distance `d`?
View SolutionIn the fig as shown a certain mass `M` is free to slide without friction on a horizontal table. This mass is connected by a light thread to a mass `m` that hangs over the edge of the table. The connecting thread passes over a frictionles pulley in the shape of a disk with radius `R` and mass `m_(p)`. Calculate the velocity of the string after the hanging mass has fallen a distance `h` starting from test.

View SolutionA wooden frame consists of seven thin rods as shown in fig.
(a) Calculate the moment of inertias of the frame for rotation about its lower edge. Take the mass and length of each rod to be `m` and `l` respectively.
(b) If the frame starts from vertical with zero speed and falls over how fast is the edge traveling just before it hits the ground?
View SolutionSuppose a person of mass `m` stands at the edge of a circular platform of radius `R` and moment of inertia `I`. The platform is at rest initially, but the platform begins to rotate when the person begins to move with velocity `v`. Determine the angular velocity of the platform.
View SolutionThe device shown in Fig. rotates on the vertical axle as shown. The frame has negligible mass as compared to the four masses each of mass `m`. Initial angular velocity of the system is `omega_(0)`. Due to an internal mechanism the spokes in the frame lengthen so that the radii of the masses become `2a`. Initially, it was a. What will be the new angular velocity of the system?
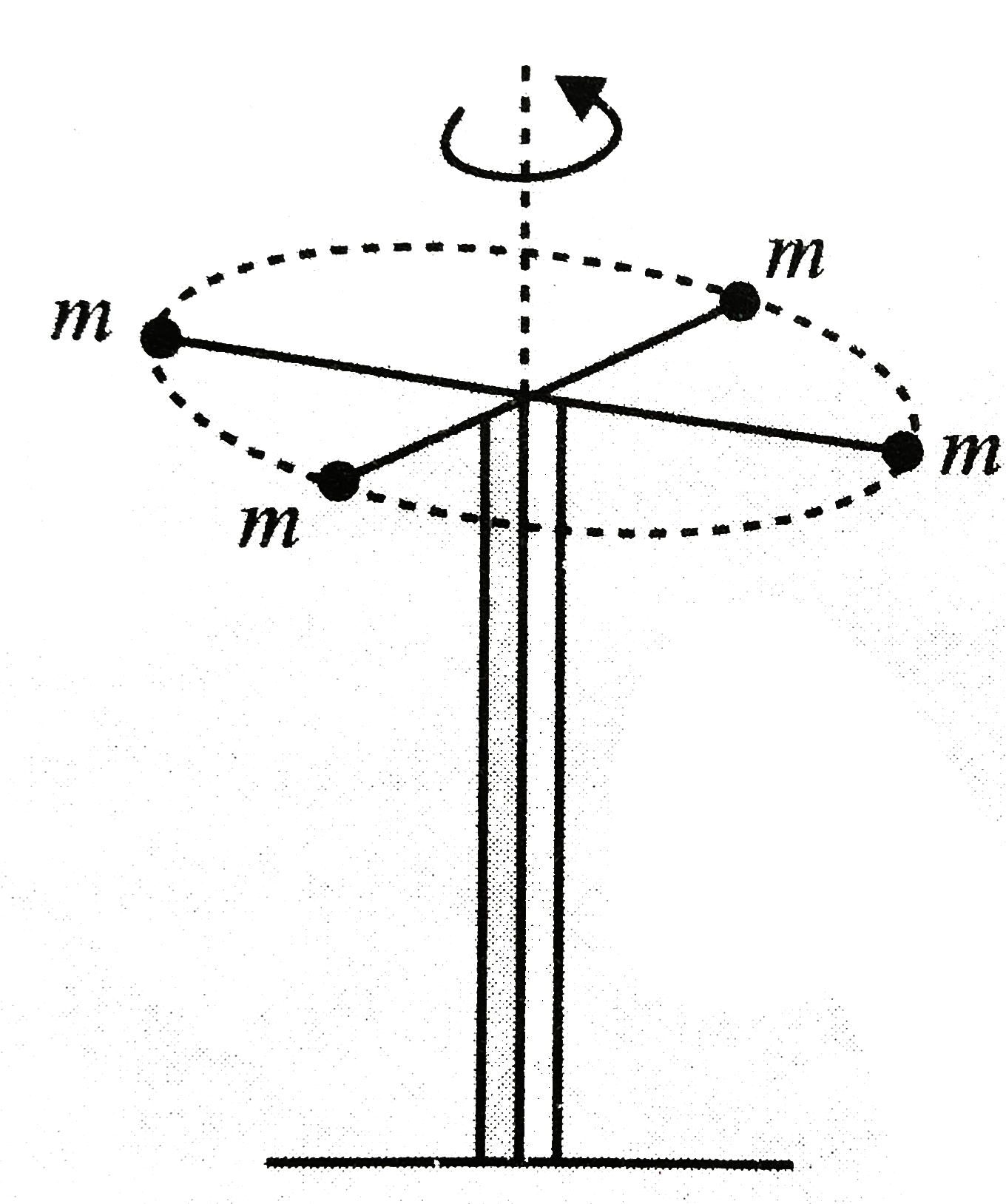
View SolutionA rotating star has a period of 30 days about an axis passing through its centre. The star undergoes an internal explosion and converts to a neutron star. Initial radius of the core was `1.0xx10^(4)` km, whereas, final radius is `3.0km`. Determine the period of rotation of the neutron star.
View SolutionA clutch assembly consists of two discs `A` and `B` of moment of inertia `2I` and `I` respectively, one being the engine fly wheel, the other one is the clutch plate. The discs are initially rotaing with angular velocities `omega_(A)=omega` and `omega_(B)=2omega` as shown in fig. When the two disc are brought into contact the discs rub against each other and eventually reach a common angualr velocity `omega`.
(a) Derive an expressio for `omega`
(b) What is the angular impulse of friction on any one of the discs?

View SolutionA man of mass `100 kg` stands at the rim of a turtable of radius `2 m` and moment of inertia `4000 kgm^(2)` mounted on a vertical frictionless shaft at its centre. The whole system is initially at rest. The man now walks along the outer edge of the turntable with a velocity of `1m//s` relative to the earth
a. With what angular velocity and in what direction does the turntable rotate?
b. Through what angle will it have rotated when the man reaches his initial position on the turntable?
c. Through what angle will it have rotated when the man reaches his initial position relative to the earth?
View SolutionTwo skaters each of mass `50 kg`, approach each other along parallel paths separated by `3m`. They have equal ad opposite velocities of `10 m//s`. The first skater carries a long light pole, `3 m` long, and the second skater grabs the end of it as he passes (assume frictionless ice).
a. Described quantitatively the motion of the skaters after they are connected by the pole.
b. By pulling on the skaters reduce their distance to `1m`. What is their motion then?
c. Compare the `KEs` of the system in parts a. and b. where does the change come from?
View SolutionA bullet of mass `m` moving with velocity `v` strikes and becomes embedded at the edge of a cylinder of mass `M` and radius `R_(0)` as shown in fig. The cylinder, initially at rest, begins to rotate about its symmetry axis, which remains fixed in position. Assuming no frictional torque, what is the angular velocity of the cylinder after this collision? Kinetic energy conseved?

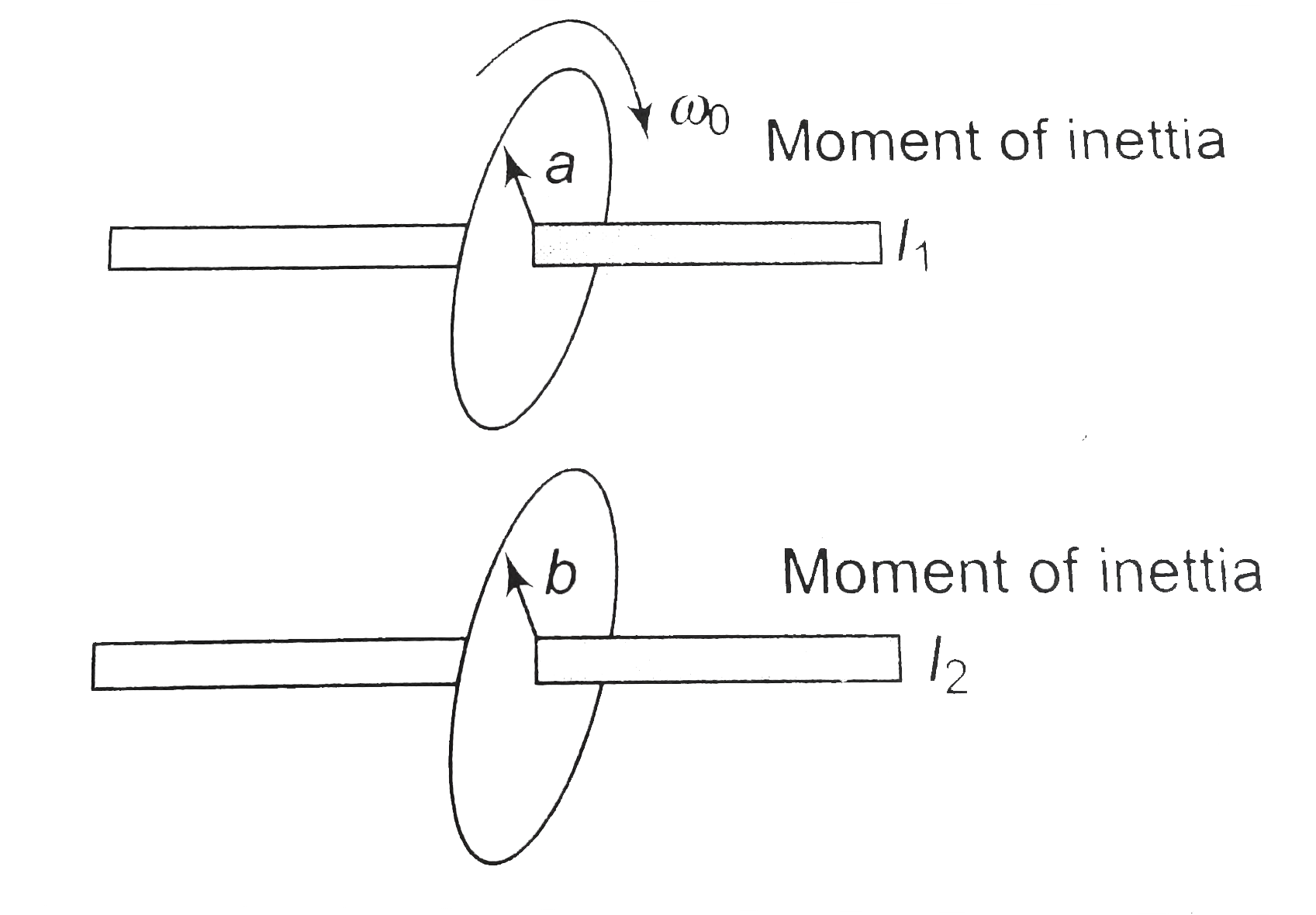
View SolutionThe two uniform discs rotate separately on parallel axles. The upper disc (radius `a` and momentum of inertia `I_1`) is given an angular velocity `omega_0` and the lower disc of (radius `b` and momentum of inertia `I_2`) is at rest. Now the two discs are moved together so that their rims touch. Final angular velocity of the upper disc is.
 .
.
View SolutionA string is wrapped several times on a cylinder of mass `M` and radius `R`. the cylinder is pivoted about its adxis of block symmetry. A block of mass `m` tied to the string rest on a support positioned so that the string has no slack. The block is carefully lifted vertically a distance `h`, and the support is removed as shown figure.
a. just before the string becomes taut evalute the angular velocity `omega_(0)` of the cylinder ,the speed `v_(0)` of the falling body, `m` and the kinetic energy `K_(0)` of the system.
b. Evaluate the corresponding quanitities `omega_(1), v_(1)` and `K_(1)` for the instant just after the string becomes taut.
c. Why is `K_(1)` less than `K_(0)`? Where does the energy go?
d. If `M=m`, what fraction of the kinetic energy is lost when the string becomes taut?
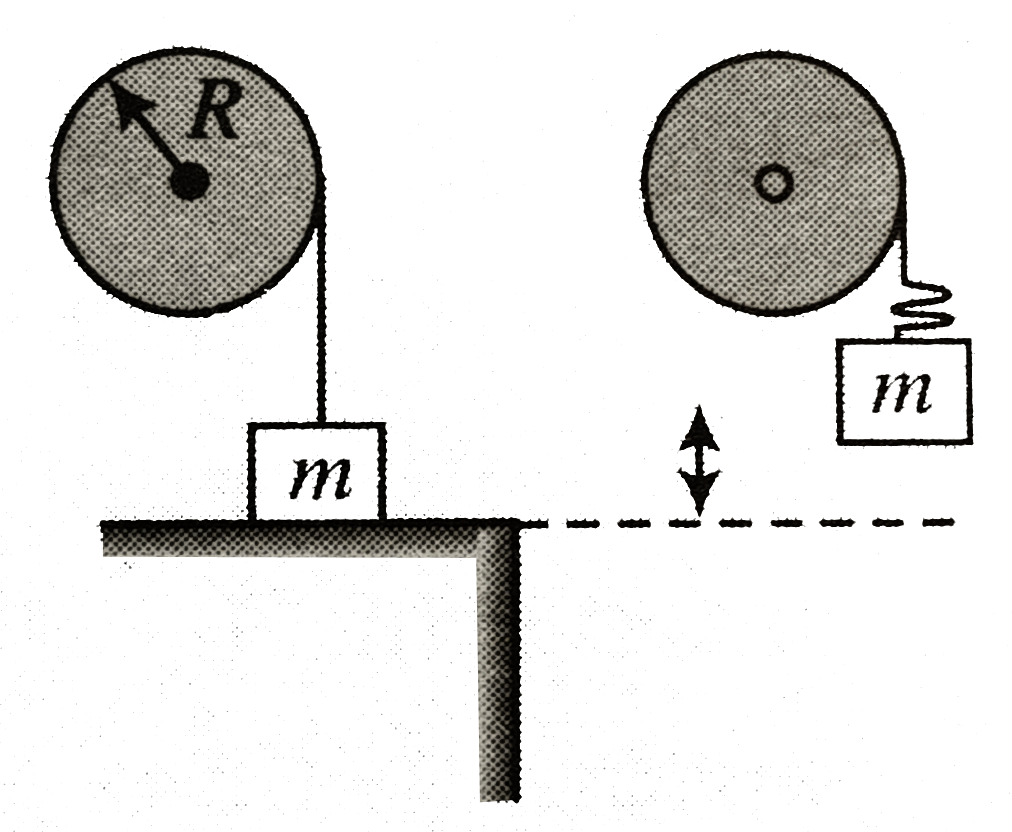
View SolutionA small mass particle is projected with an initial velocity `v_(0)` tangent to the horizontal rim of smooth hemisphereical bowl at a radius `r_(0)` from the vertical centre line, as shown at point A. As the particle slide past point `B`, a distance `h` below `A` and distance `r` from the verticle centre line, its velocity `v` makes an angle `theta` with the horizontal tangent to the bowl through `B`. Determine `theta`.

View SolutionA uniform rectangular block of dimensions shown in fig is sliding on the horizontal surface with a velocity `v` when it strikes a small kerb in the surface. Determine the minimum value of `v` for which the block will pivot about the kerb and just reach the vertical position with no velocity. Assume negligible rebound at the step.

View SolutionA thin uniform rod of length `l` is initially at rest with respect to an inertial frame of reference. The rod is tapped at one end perpendicular to its length. How far the centre of mass translates while the rod completes one revolution about its centre of mass. Neglect gravitational effect.
View SolutionA wedge of mass m and triangular cross- section (AB = BC = CA = 2R) is moving with a constant velocity `-v hat`I towards a sphere of radius R fixed on a smooth horizontal table as shown in figure. The wadge makes an elastic collision with the fixed sphere and returns along the same path without any rotaion. Neglect all friction and suppose that the wedge remains in contact with the sphere for a very shot time. `Deltat,` during which the sphere exerts a constant force F on the wedge.
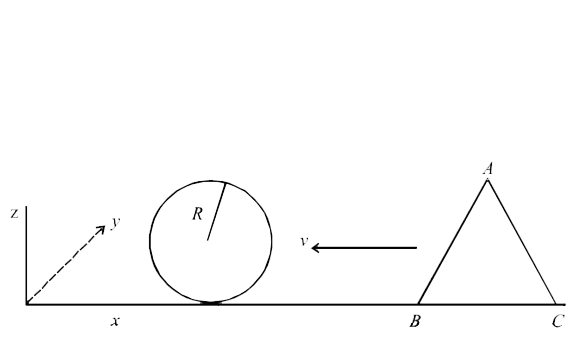
(a) Find the force F and also the normal force N exerted by the table on the wedge during the time `Deltat.`
(b) Ler h denote the perpendicular distance between the centre of mass of the wedge and the line of action of F. Find the magnitude of the torque due to the normal force N about the centre of the wedge, during the interval `Deltat.`
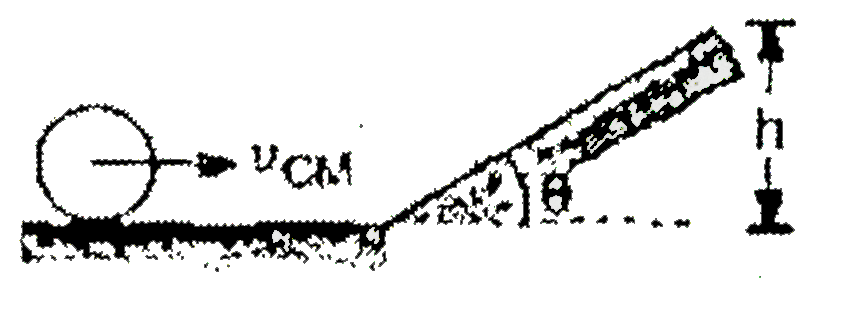
View SolutionA ball of radius `R` and mass `m` is rolling without slipping on a horizontal surface with velocity of its centre of mass `v_(CM)`. It then rolls wilthout slippig up a hill to a height `h` before momentarily coming to rest. Find `h`
View SolutionA rectangular rigid fixed block has a long horizontal edge. A solid homogeneous cylinder of radus R is placed horizontally at rest its length parallel to the edge such that the exis of the cylinder and the endg of the block are in the same vertical plane as shown in the figure below. Ther is sufficinet friction present at the edge s that a very small displacement causes the cylinder to roll off the edge without slipping. Determine:

(a) the angle `theta_c` through which the cylinder rotates before it leaves contact with the edge,
(b) the speed of the centre of mass of the cylinder before leaving contact with the edge, and
(c) the ratio of the translational to rotational kinetic energy of the cylinder when its centre of mass is in horizontal line with the edge.
View SolutionA solid cylinder has a thin string wrapped several times around its circumference. The string is fixed at one end and the cylinder is released. Find the downward acceleration of cylinder and tension in the string.
View SolutionA horizontal force `P` applied at a height `h` above the centre of a solid cylinder of mass `M`, radius `R`. Determine force of friction in terms of `h` show that friction force is zero for `h=R//2`. Assume that the cylinder rolls without slipping.
View SolutionA wheel of radius `R`, mass `m` and moment of inertia `I` is pulled along a horizontal surface by application of force `F` to as rope unwinding from the axel of radius, `r` as shown in figure. Friction is sufficient for pure rolling of the wheel.
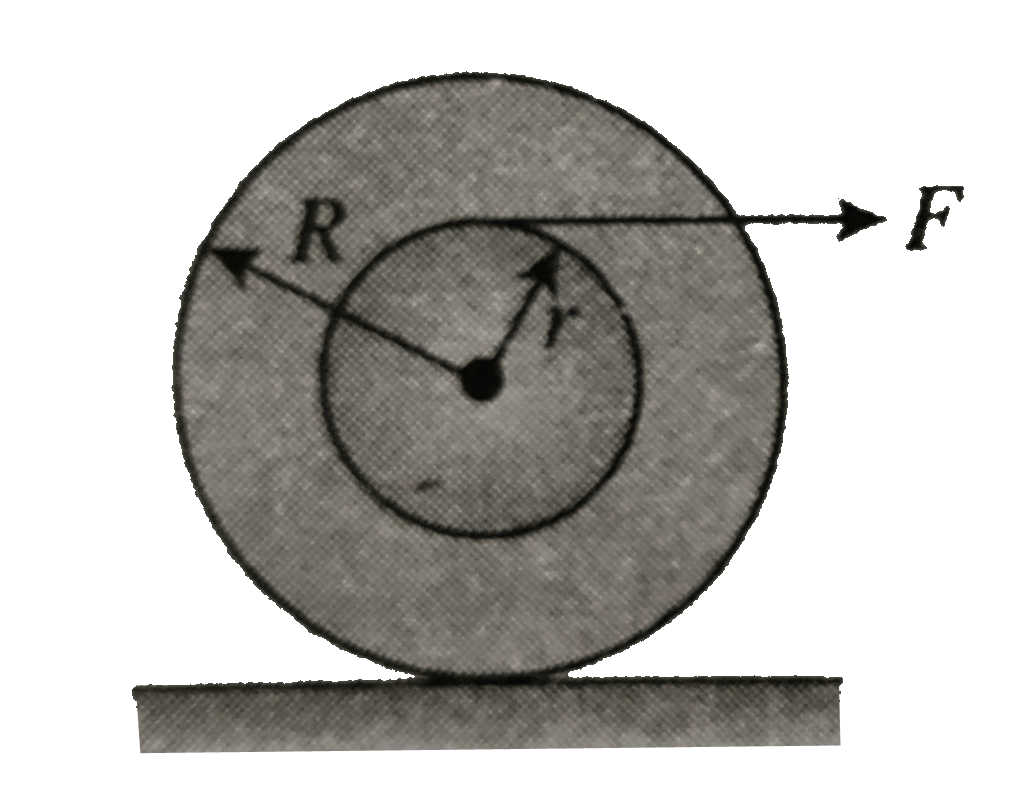
a. What is the linear acceleration of the wheel?
b. Calculate the frictional force that acts on the wheel.
View SolutionA sphereicla ball of mass `M` and radius `R` is projected along a rough horizontal surface so that initially `(t=0)` it slides with a linear speed `v_(0)` but does not rotate. As it slides, it begins to spin and eventually rolls without slipping. How long does it take to begin rolling without slipping?
View SolutionA uniform disc of mass `m` and radius `R` is projected horizontally with velocity `v_(0)` on a rough horizontal floor so that it starts off with a purely sliding motion at `t=0`. After `t_(0)` seconds, it acquires pure rolling motion as shown in the figure.
(a) Calculate the velocity of the center of mass of the disc at `t_(0)`.
Assuming that the coefficent of friction to be `mu`, calculate `t_(0)`.

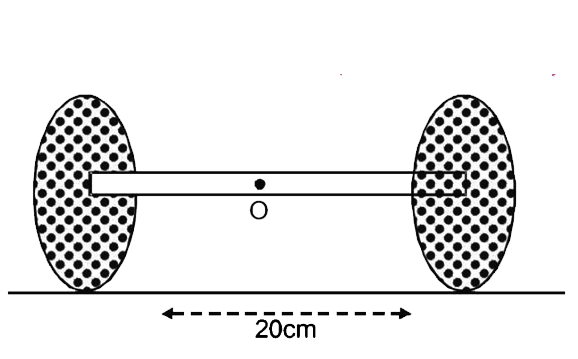
View SolutionTwo thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of `9m//s^2` Calculate:
(i) The force fo friction on each disk,
(ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors `hati, hatj and hatk` in the x,y, and z directions.
View SolutionThe cue stick hits a cue ball horizontally a distance `x` above the centre of the ball. Find the value of `x` for which the cue ball will instantaneously roll without slipping. Calculate the answer in terms of the radius `R` of the ball.

View SolutionA ball of radius `r` hits a cushion with a pure rolling motion and rebounds, with a pure rolling motion. Find the ratio of the height `h` of the cushion to the radius `r` of the ball. Assume that the foce exerted on the ball by the cushion is horizontal during the impact and that the ball hits the cushion normally.
View SolutionA diatomic molecule two identicla atoms of mass `m` bound together a distance `l` apart is confined in a lab reference frame. At a certain time one of the two atoms is observed to have speed `v_(0)` and the other, moving in the opposite direction, speed `v_(0)//3`.

View SolutionA uniform rod of length `l` and mass `2m` rest on a smooth horizontal table. A points mass `m` moving horizontally at right angles to the rod with an initial velocity `v` collides with one end of the rod and sticks to it.
Determine
(a) the angular velocity of the system after collision,
(b) the position of the point on the rod which remains stationary immediately after collision,
(c) the chabge in kinetic energy of the system as a result of the collision.
View SolutionA spinning cylinder of mass `m` and radius `R` is lowered on a rough inclined plane of angle `30^(@)` with the horizontal and `mu=1sqrt(3)`. The cylinder is released at a height of `3R` from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline.
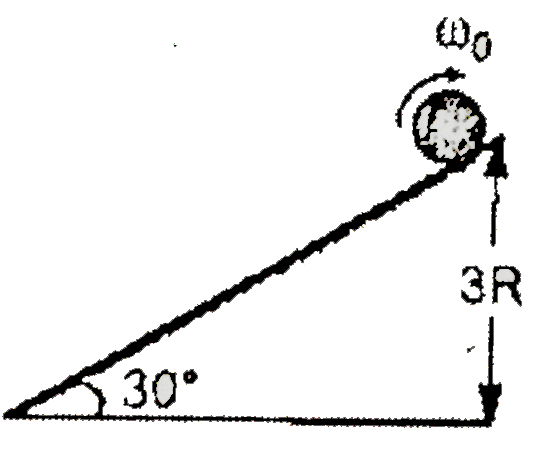
View Solution
EXAMPLE_TYPE questions and complete solutions for chapter RIGID BODY MOTION of SHREE BALAJI PHYSICS (HINGLISH) of Class 11