Complete Solutions to SCQ_TYPE of chapter RIGID BODY MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | RIGID BODY MOTION |
| ANURAG MISHRA | SCQ_TYPE |
| Number Of Questions | 83 |
| Academic Year | 2023-24 |
A homogenous rod of length `l=etax` and mass `M` is lying on a smooth horizontal floor. A bullet of mass `m` hits the rod at a distance `x` from the middle of the rod at a velocity `v_(0)` perpendicular to the rod and comes to rest after collision. If the velocity of the farther end of the rod just after the impact is in the opposite direction of `v_(0)` then:
View SolutionA thin circular ring of mass M and radius r is rotating about its ais with an angular speed `omega`. Two particles having mas m each are now attached at diametrically opposite points. The angular speed of the ring will become
View SolutionA flywheel rotates about an axis. Due to friction at the axis, it experiences an angular retardation proportional to its angular velocity. If its angular velocity falls to half while it makes `n` rotations, how many more rotations will it make before coming to rest?
View SolutionThe figure shows a uniform rod lying along the `x`-axis. The locus of all the points lying on the `x-y` plane, about which the moment of inertia of the rod is same as that about `O`, is

View SolutionThe moment of inertia of a uniform semicircular disc of mass `M` and radius `r` about a line perpendicular to the plane of the disc through the center is
View SolutionA ring of mass `M` and radius `R` is released on an inclined as shown. If the coefficient of friction `mu lt 1/2 tan theta`, then during a displacement `l`:
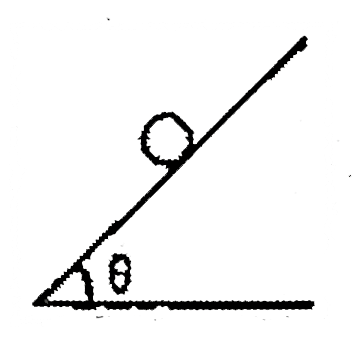
View SolutionThe line of action of the resultant of two like parallel forces shifts by one-fourth of the distance between the forces when the two forces are interchanged. The ratio of the two forces is:
View SolutionA mass m moving with a constant velocity along a line parallel to the axis, away from the origin. Its anguarl momentum with respect to the origin
View SolutionA person sitting firmly over a rotating stool has his arms stretched. If he folds his arms, his angular momentum about the axis of rotation
View SolutionTwo uniform rods of equal length but different masses are rigidly joined to form an `L`-shaped body, which is then pivoted about `O` as shown. If in equilibrium the body is in the shown configuration, ratio `M/m` will be

View SolutionA solid sphere of mass `M`, radius `R` and having moment of inertia about as axis passing through the centre of mass as `I`, is recast into a disc of thickness `t`, whose moment of inertia about an axis passing through its edge and perpendicular to its plance remains `I`. Then, radius of the disc will be.
View SolutionA mass m moving with a constant velocity along a line parallel to the axis, away from the origin. Its anguarl momentum with respect to the origin
View SolutionAn cylinder of mass `m` is rotated about its axis by an angular velocity `omega` and lowered gently on an inclined plane as shown in figure. Then :
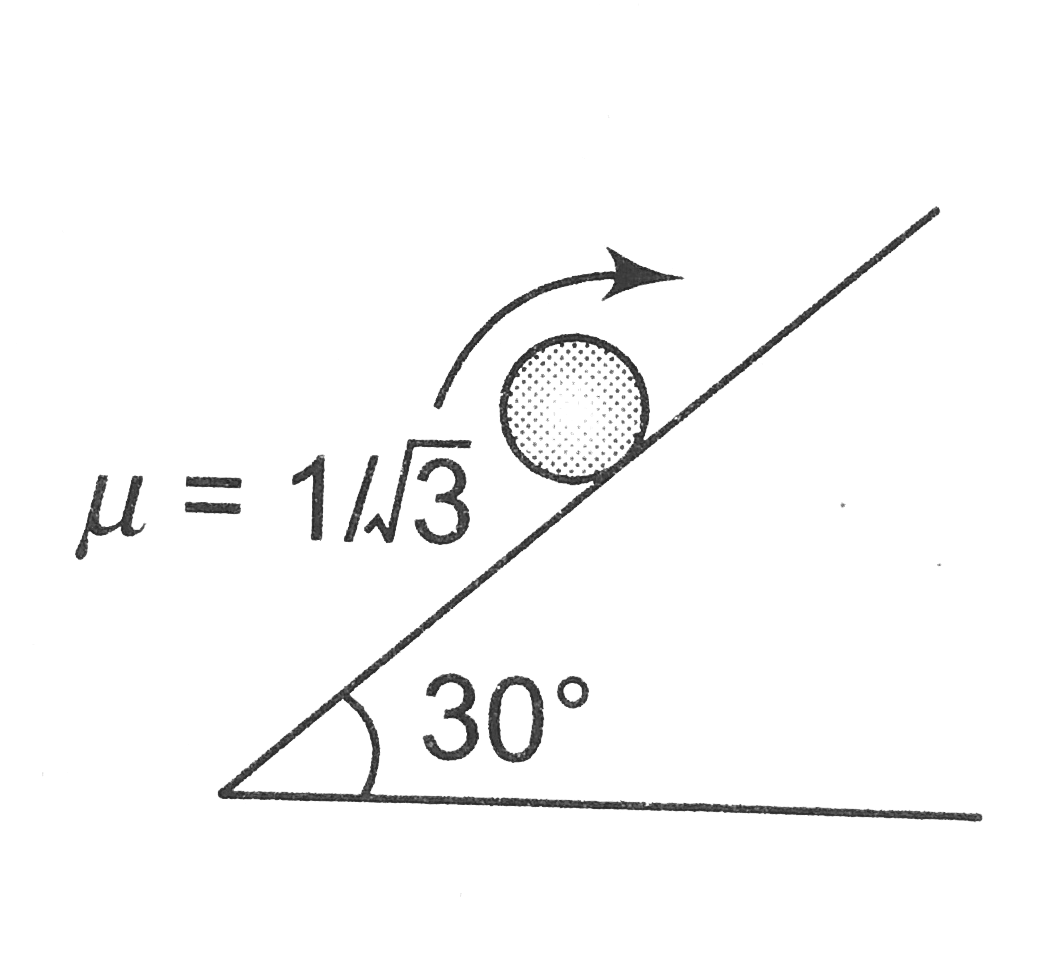 .
.
View SolutionA wheel of radius `R` rolls without slipping on a horizontal ground. The distance travelled by a point on the rim in one complete rotation is:
View SolutionTwo identical rods are joined to form an `'X'`. The smaller angle between the rods is `theta`. The moment of inertia of the system about an axis passing through point of intersection of the rods and perpendicular to their plane is proportional to:
View SolutionOne end of a uniform rod of mas m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a unifrom angular velocity `omega`. Theforce exerted by the clamp on the rod has a horizontal component
View SolutionA large platform is moving with constant acceleration `'a'` perpendicular to its plane in gravity free space. A particle of mass `m` is projected with speed `u` relative to the platform at an angle `theta` with its plane from a point `O` on it. The angular momentum of the particle about `O`:
View SolutionA cubical block of side a is moving with velocity V on a horizontal smooth plane as shown in Figure. It hits a ridge at point O. The angular speed of the block after it hits O is
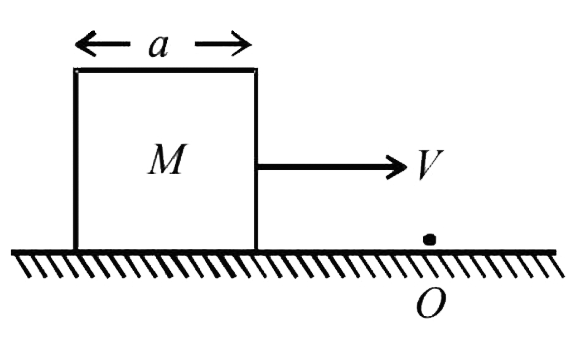
View SolutionA wheel of radius `r` rolls without slipping with a speed `v` on a horizontal road. When it is at a point `A` on the road, a small blob of mud separates from'the wheel at- its highest point and lands at point `B` on the road:
View SolutionA string of negligible thicknes is wrapped several times around a cylinder kept on a rough horizontal surface. A man standing at a distance l from the cylinder holds one end of the sitting an pulls the cylinder towards him figure. There is no slipping anywhere. The length of the string passed through the hand of the man whicle the cylinder reaches his hands is

View Solution`ABC` is a traiangular plate of uniform thickness. The sides are in the ratio shown in the figure. `I_(AB)`, `I_(BC)` and `I_(CA)` are the moments of inertia of the plate about `AB`, `BC` and `CA` repectively. Which one of the following relations is correct?
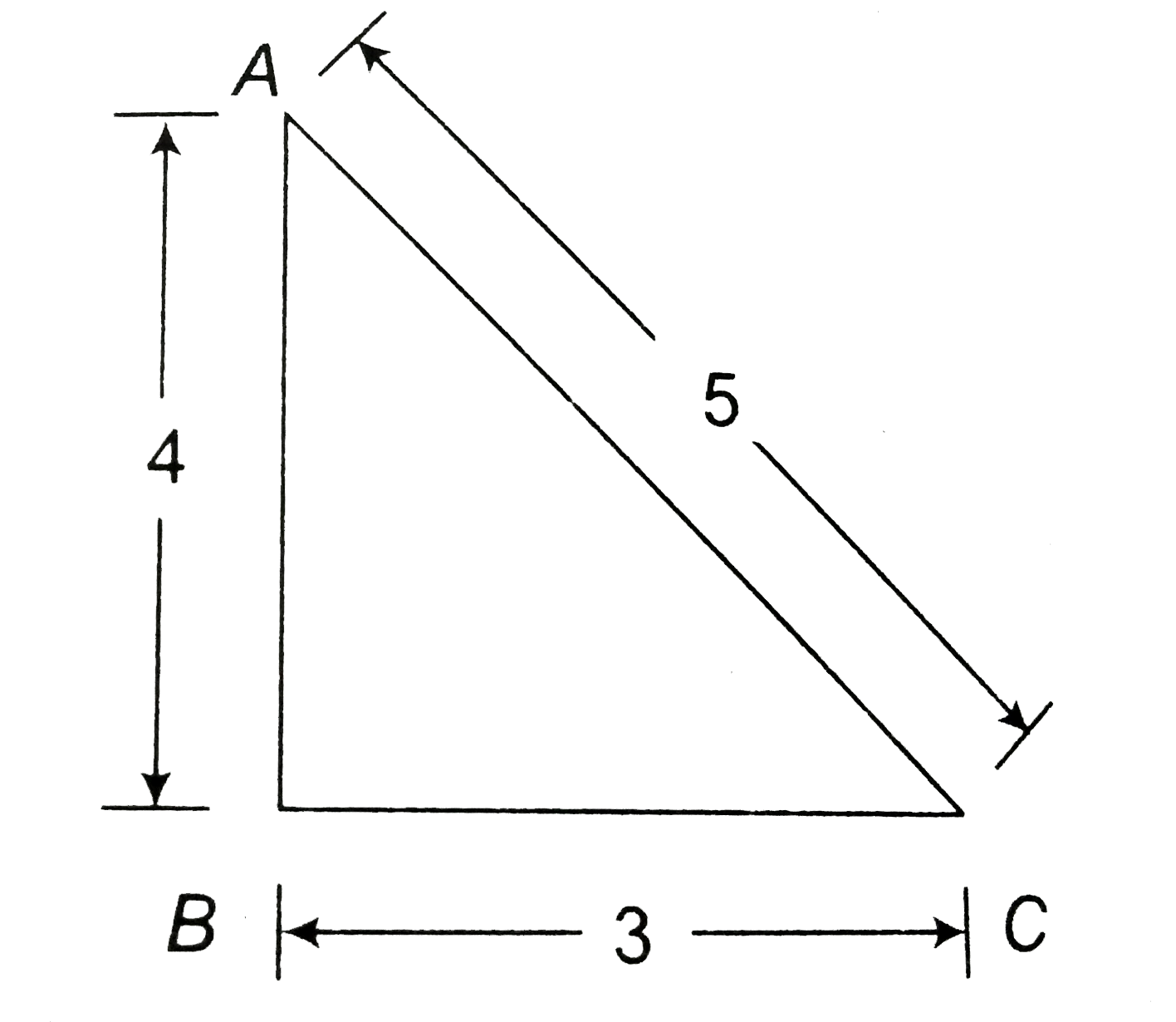
View SolutionA solid homogeneous sphere of mass `M` and radius `R` is moving on a rough horizontal surface partly rolling and partly sliding. During this kind of motion of the sphere
View SolutionLer l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle `theta` with AB. The moment of inertia of the plate about the axis CD is then equal to
View SolutionTwo uniform solid spheres having unequal rdii are released from rest from the same height on a rough incline. Ilf the spheres roll without slipping
View SolutionA particle of mass `m=5 kg` is moving with a uniform speed `v=3 sqrt(2)` in the `XOY` plane along the line `Y=X+4`. The magnitude of the angular momentum of the particle about the origin is
View SolutionA sphere `S` rolls without slipping moving with a constant speed on a plank `P`. The friction between the upper surface of `P` and the sphere is sufficient to prevent slipping, while the lower surface of `P` is smooth and rest on the ground. Initially `P` is fixed on the ground by a pin `N`. If `N` is suddenly removed

View SolutionThree identical solid spheres move down three incline `A, B` and `C` are all of the same dimensions. A is without friction, the friction between `B` and a sphere is sufficient to cause rolling without slipping, the friction between `C` and a sphere causes rolling with slipping. The kinetic energies, of `A, B, C` at the bottom of the inclines are `E_(A),E_(B),E_(C)`.
View SolutionA sphere is rotating about a diameter
View SolutionA thin spherical shell of radius `R` lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
View SolutionTwo moving particles `P` and `Q` are 10cm apart at any instant. Velocity of P is `8 m//s` at `30^(@)`, from line joining the P and Q and velocity of Q is `6m//s` at `30^(@)`. Calculate the angular velocity of P w.r.t. Q
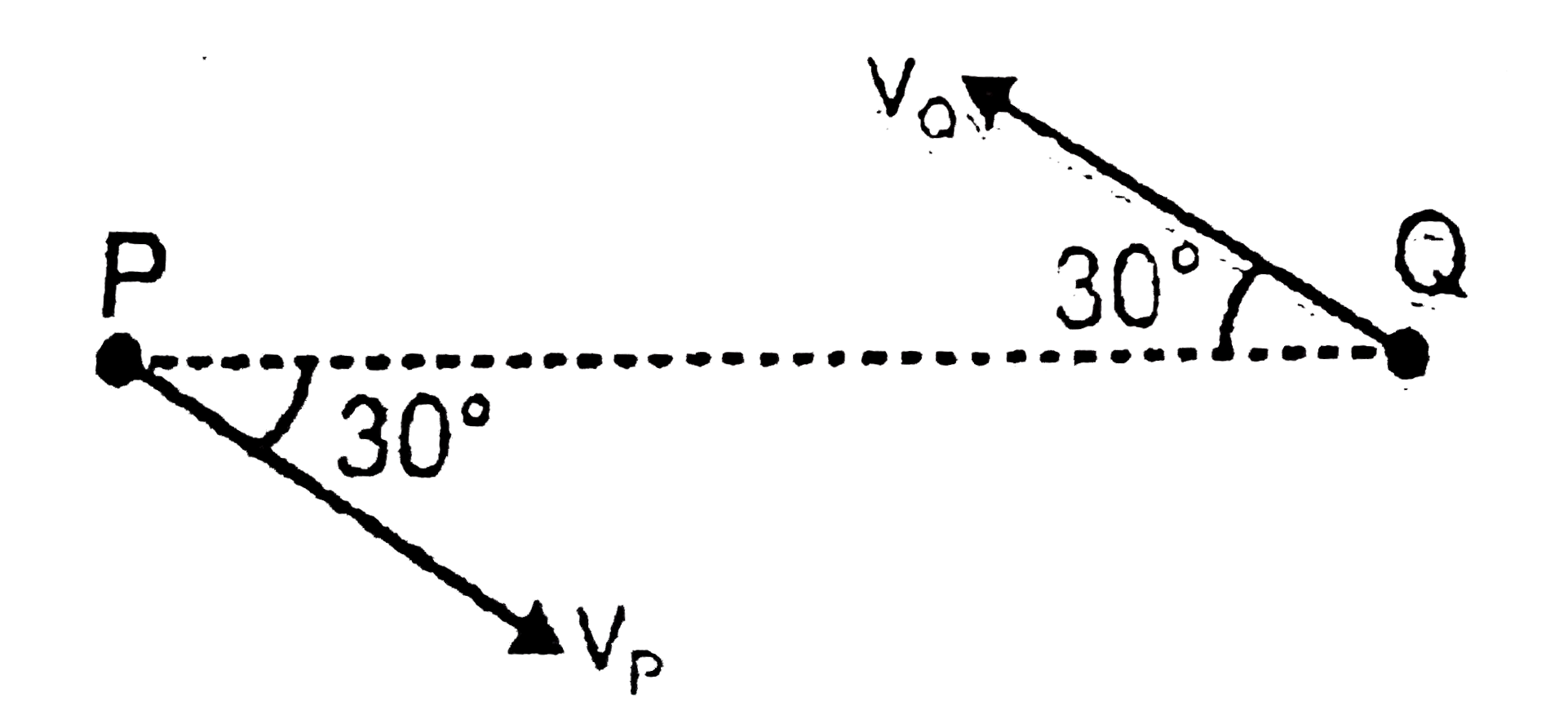
View SolutionA uniform rod of mass `m` and length `l_(0)` is rotating with a constant angular speed `omega` about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle `theta` to the vertical (axis of rotation).
View SolutionA sphere can roll on a surface inclined at an angle `theta` if the friction coefficient is more than `(2)/(7) g sin theta`. Suppose the friction coefficient is `(1)/(7) g sin theta`, and a sphere is released from rest on the incline,
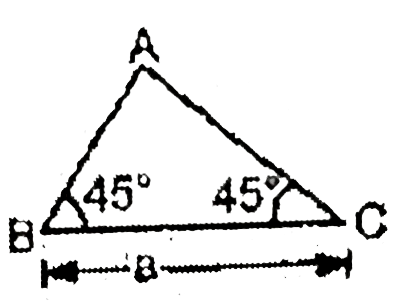
View SolutionWhat is the moment of inertia of a triangular plate `ABC` of mass `M` and side `BC='a'` about a axis passing through `A` and perpedicular to the plane of the plate?
View SolutionA rolling body is kept on a plank B. There is sufficient friction between `A` and `B` and no friction between `B` and the incline,d plane. Then body:

View SolutionThree identical rods, each of length `L`, are joined to form a rigid equilateral triangle. Its radius of gyration about an axis passing thorugh a corner and perpendicular to plane of triangle is
View SolutionA sphere cannot roll on
View SolutionFigure shows smooth inclined plane fixed in a car acceleratiing on a horizontal road. The angle of incline `theta` is related to the acceleration a of the car as `a=gtantheta`. If the sphere is set in pure rolling on the incline

View SolutionA uniform rod is kept vertically on a horizontally smooth surface at a point O. IF it is rotated slightly and released, it falls down on the horizontal surface. The lower end will remain
View SolutionA uniform rod of length `l` and mass `M` is suspended on two vertical inextensible string as shown in figure. Then tension `T` in the left string at the instant, when right string snaps is?

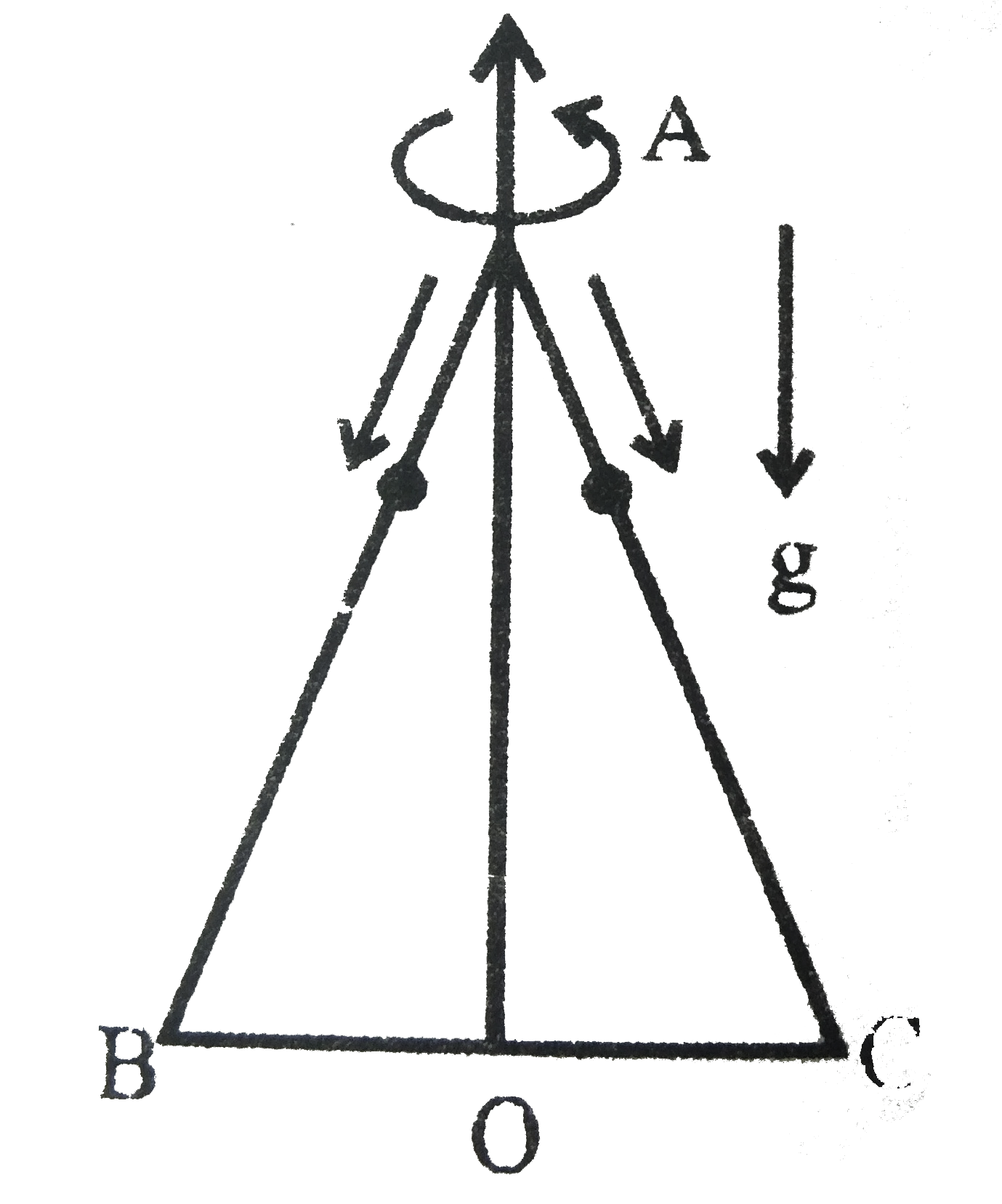
View SolutionA equilaterial triangle `ABC` formed from a uniform wire has two small identical beads initially located at `A`. The triangle is set rotating about the vertical axis `AO`. Then the beads are released from rest simultaneously and allowed to slide down. one long. `AB` and the other along `AC` as shown. Neglecting frictional effects, the quantities that are conserved as the beads slide down, are.
 .
.
View SolutionA translational velocity `v_(0)` is imparted in a horizontal direction to a hoop of radius `r` placed on a rough horizontal surface. What is angular velocity of hoop after it stops slipping?
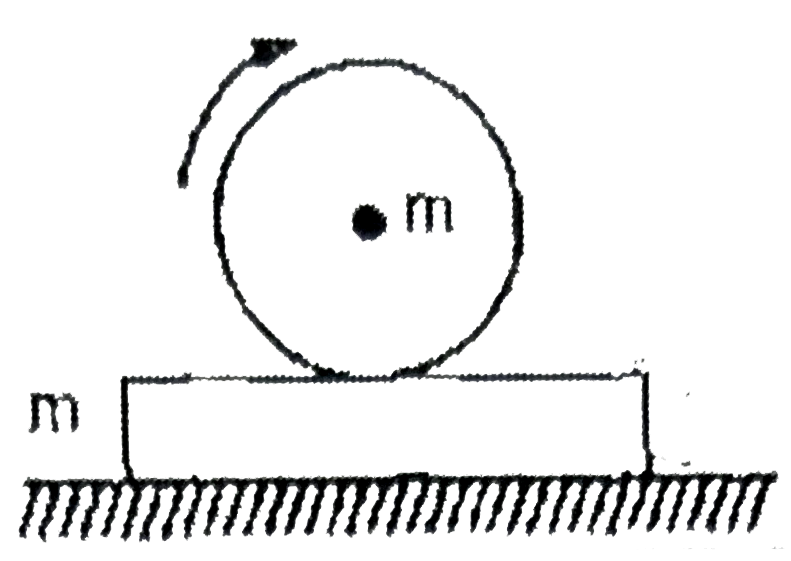
View SolutionA sphere of mass `m` is given some angular velocity about a horizontal axis through the center, and gently placed on a plank of mass `m`. The coefficient of friction between the two is `mu`. The plank rests on a smooth horizontal surface. The intial acceleration of the sphere relative to the plank will be:
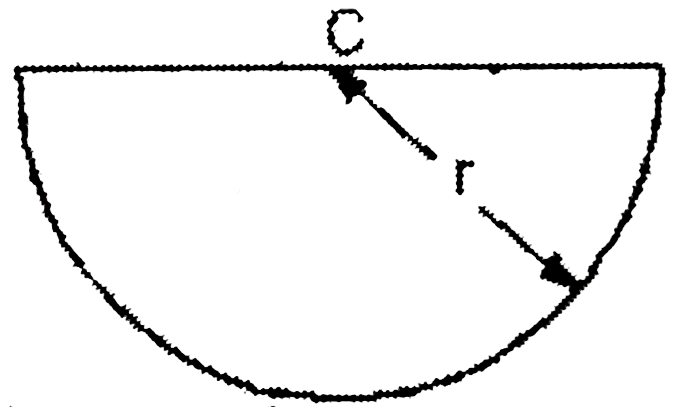
View SolutionA semicircular lamina of mass `m` and radius `'r'` and centre `C`. Its center of mass is at a distance `'x'` from `C`. Its moment of inertia about an axis through its center of mass and perpendicular to its plane is:
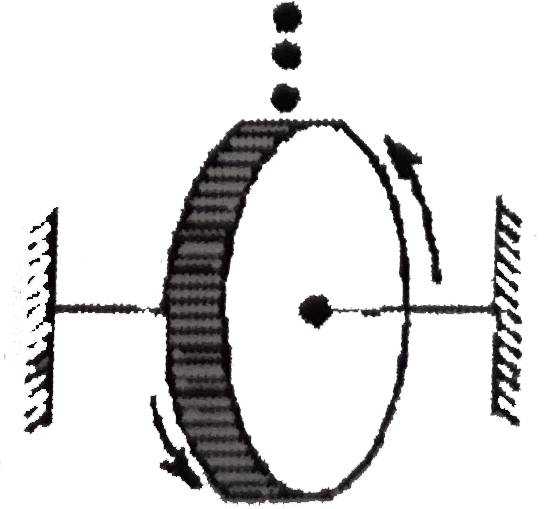
View SolutionA disc of mass m0 rotates freely about a fixed horizontal axis through its center. A thin cotton pad is fixed to its rim, which can absorb water. The mass of water dripping onto the pad is `mu` per second. After what time will the angular velocity of the disc get reduced to half of its initial value:
View SolutionA plank `P` is placed on a solid cylinder `S`, which rolls on a horizontal surface. The two are of equal mass. There is no slipping at any of the surfaces in contact. The ratio of kinetic energy of `P` to the kinetic energy of `S` is:

View SolutionA thin wire of length `L` and uniform linear mass density `rho` is bent into a circular loop with centre at `O` as shown. The moment of inertia of the loop about the axis `XX'` is :
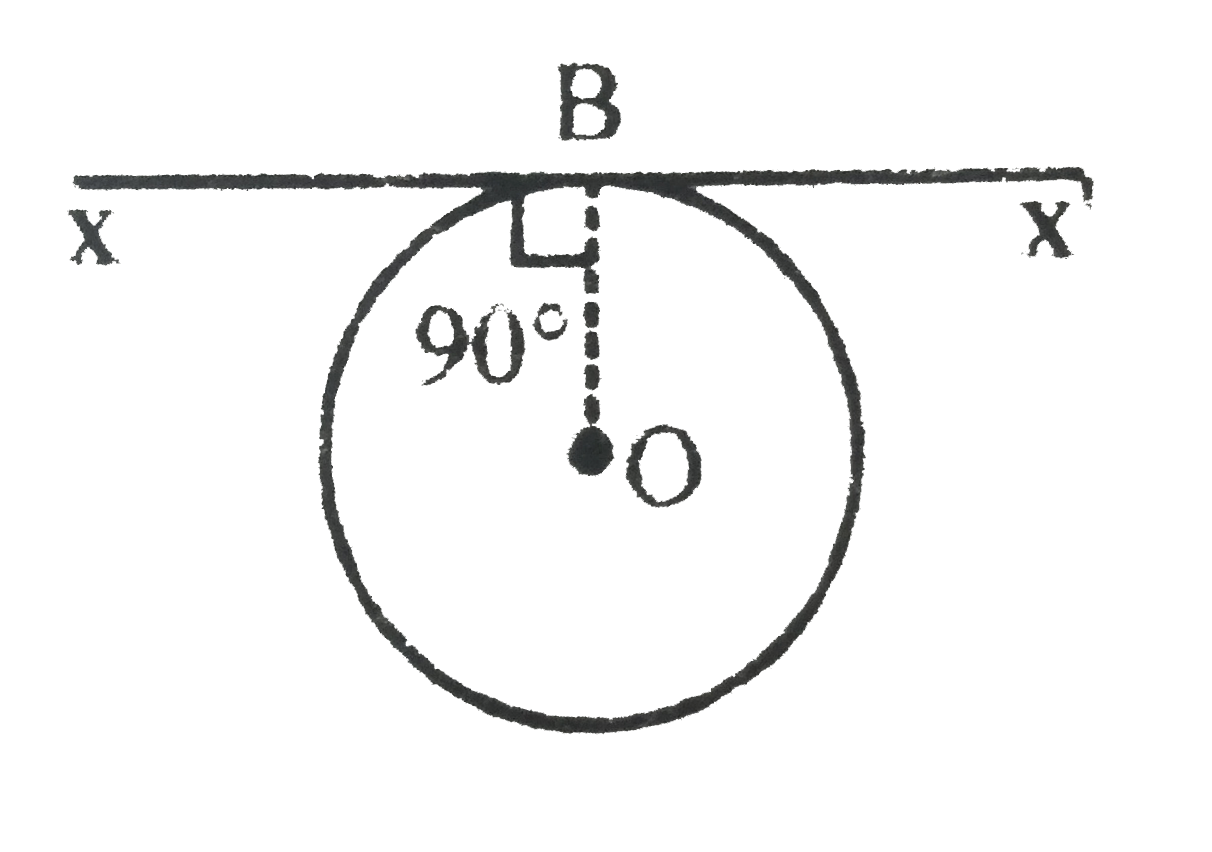 .
.
View SolutionA round uniform body of radius `R`, mass `M` and moment of inertia 'I' rolls down (without slipping) and inclined plane making an angle `theta` with the horizontal. Then its acceleration is.
View SolutionA thin rod of mass `m` and length `l` is hinged at the lower end to a level floor and stands vertically. Then its upper end will strike the floor with a velocity given by:
View SolutionA cubical block of side L rests on a rough horizonta surface with coefficient of friction `mu`. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is

View SolutionOne quarter sector is cut from a uniform circular disc of radius `R`. This sector has mass `M`. It is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. It moment of inertia about the axis of rotation is.
 .
.
View SolutionA cylinder rolls up an inclined plane, reaches some height, and then rolls down (without slipping throughout these motions). The directions of the frictional force acting on the cylinder are.
View SolutionA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity `omega_(0)`. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform),
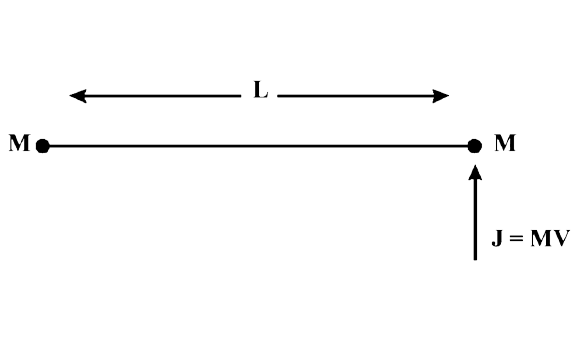
View SolutionConsider a body, shown in figure, consisting of two identical balls, each of mass M connected by a light rigid rod. If an impulse J = MV is imparted to the body at one of its ends what would be it angular velocity?
View SolutionA particle undergoes uniform circular motion. About which point on the plane of the circle, will the angular momentum of the particle remain conserved?
View SolutionA disc is rolling (without slipping) on a horizontal surface. `C` is its center and `Q` and `P` are two points equidistant from `C`. Let `V_(P), V_(Q)` and `V_(C)` be the magnitude of velocities of points `P, Q` and `C` respectively, then
 .
.
View SolutionA child is standing with folded hands at the center of a platform rotating about its central axis. The kinetic energy of the system is `K`. The child now stretches his arms so that the moment of inertia of the system doubles. The kinetic energy of the system now is
View SolutionA particle moves in a circular path with decreasing speed . Choose the correct statement.
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionA 'T' shaped object with dimensions shown in the figure, is lying on a smooth floor. A force `'vecF'` is applied at the point P parallel to AB, such that the object has only the translational motion without rotation. Find the location of P with respect C.
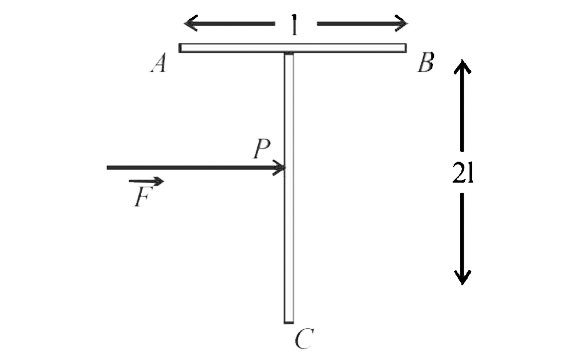
View SolutionA thin circular ring of mass `m` and radius `R` is rotating about its axis with a constant angular velocity `omega`. Two objects each of mass `M` are attached gently to the opposite ends of a diameter of the ring. The ring now rotates with an angular velocity `omega' =`
View SolutionA force of `-Fhatk` acts on O, the origin of the coodinate system. The torque about the point (1,-1) is
View SolutionFour point masses, each of value `m`, are placed at the corners of square `ABCD` of side `l`. The moment of inertia of this system about an axis passing through `A` and parallel to `BD` is -
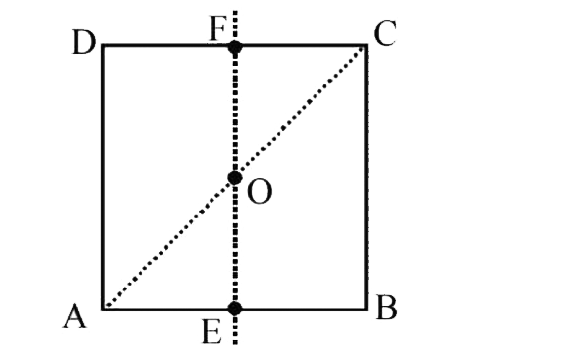
View SolutionFor the given uniform square lamina ABCD, whose centre is O,
View SolutionA uniform thin bar of mass `6 m` and length `12 L` is bend to make a regular hexagon. Its moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the hexagon is :
View SolutionTwo rings of same radius and mass are placed such that their centres are at a common point and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the centre and perpendicular to the plane of one of the rings is (mass the ring `= m`, radius `= r`)
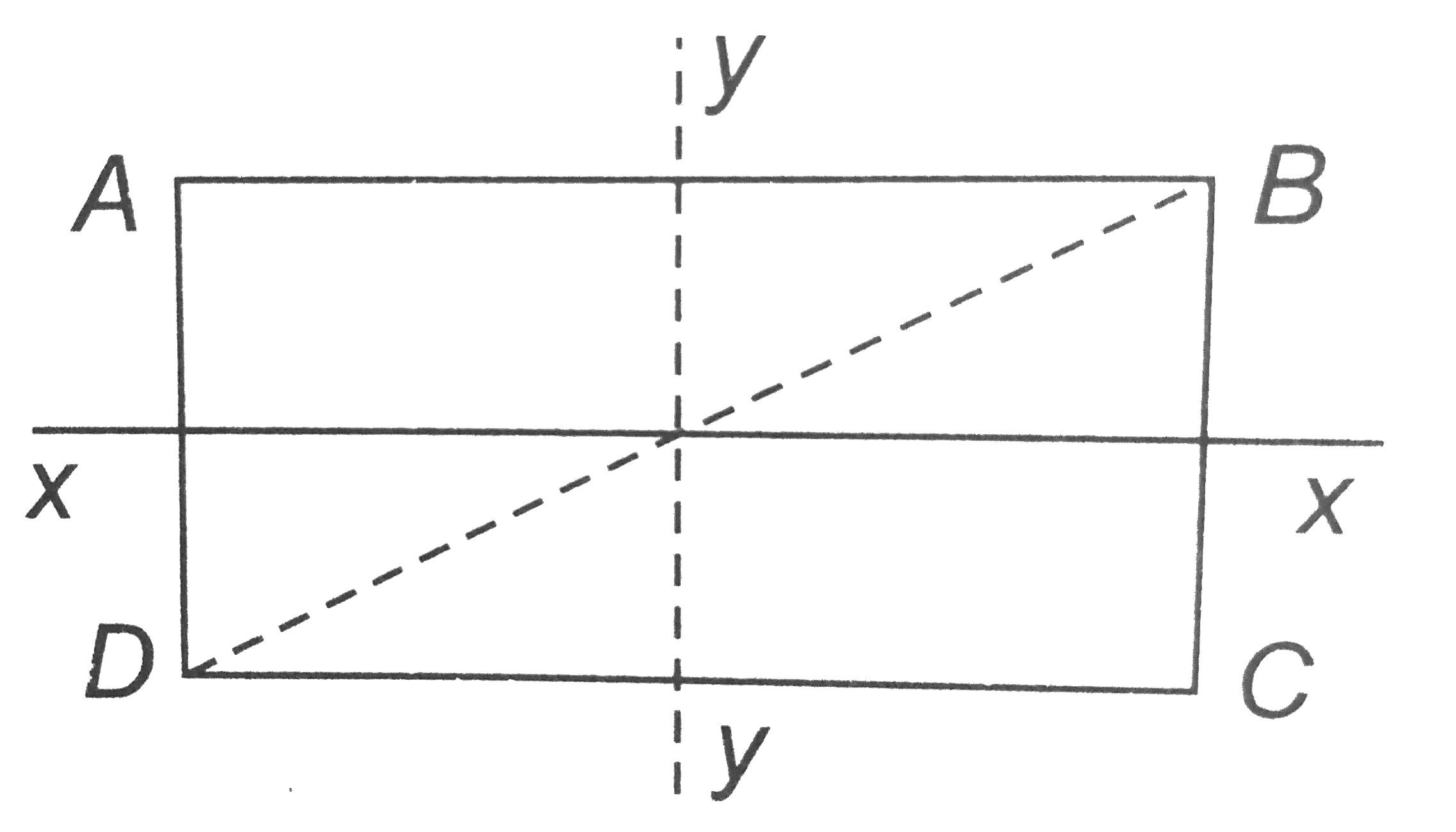
View SolutionIn a rectangle `ABCD, AB = 21` and `BC = 1`. Axes `xx` and `yy` pass through centre of the rectangle. The moment of inertia is least about :
 .
.
View SolutionMoment of inertia `I` of a solid sphere about an axis parallel to a diameter and at a distance `x` from it varies as:
View SolutionA wire of length `l` and mass `m` is bent in the form of a rectangle `ABCD` with `(AB)/(BC)=2`. The moment of inertia of this wife frame about the side `BC` is
View SolutionA hoop rolls on a horizontal ground without slipping with linear speed `v`. Speed of a particle `P` on the circumference of the hoop at angle `theta` is :
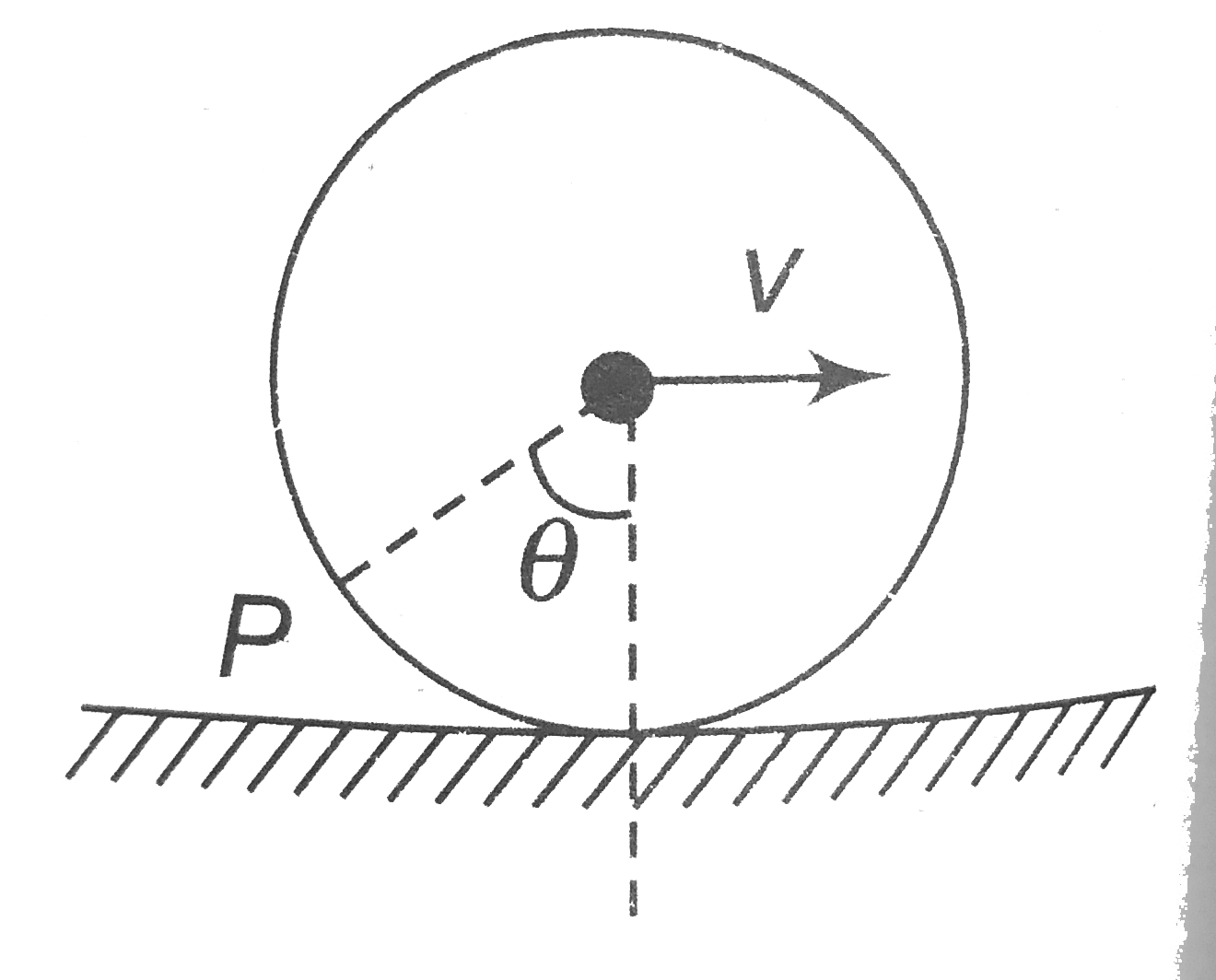
View SolutionA rigid spherical body is spinning around an axis without any external torque. Due to temperature its volume increases by `3%`. Then percentage change in its angular speed is:
View SolutionA solid sphere and a hollow sphere of equal mass and radius are placed over a rough horizontal surface after rotating it about its mass centre with same angular velocity `omega_(0)`. Once the pure rolling starts let `v_(1)` and `v_(2)` be the linear speeds of their centres of mass. Then
View SolutionA circular platform is mounted on a vertical frictionless axle. Its radius is `r=2m` and its moment of inertia is `I=200kg-m^(2)`. It is initially at rest. A `70kg` man stands on the edge at speed `v_(0)=1.0m//s` relative to the ground. The angular velocity of the platform is:
View SolutionA ball of mass `m` and radius `r` rolls inside a hemispherical shell of radius `R`. It is released from rest from point `A` as shown in figure. The angular velocity of centre of the ball in position `B` about the centre of the shell is.
 .
.
View SolutionA disc of radius `0.1m` rolls without sliding on a horizontal surface with a velocity of `6m//s`. It then ascends a smooth continuous track as shwon in figure. The height upto which it will ascend is `(g=10m//s^(2))`

View SolutionA sphere is moving on a smooth surface with linear speed `v_(0)` and angular velocity `omega_(0)`. It finds a rough inclined surface and it starts climbing up:

View SolutionAn inclined plane makes an angle of `60^(@)` with horizontal. A disc rolling acceleration equal to:
View SolutionA force `F` is applied at the top of a ring of mass `M` and radius `R` placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

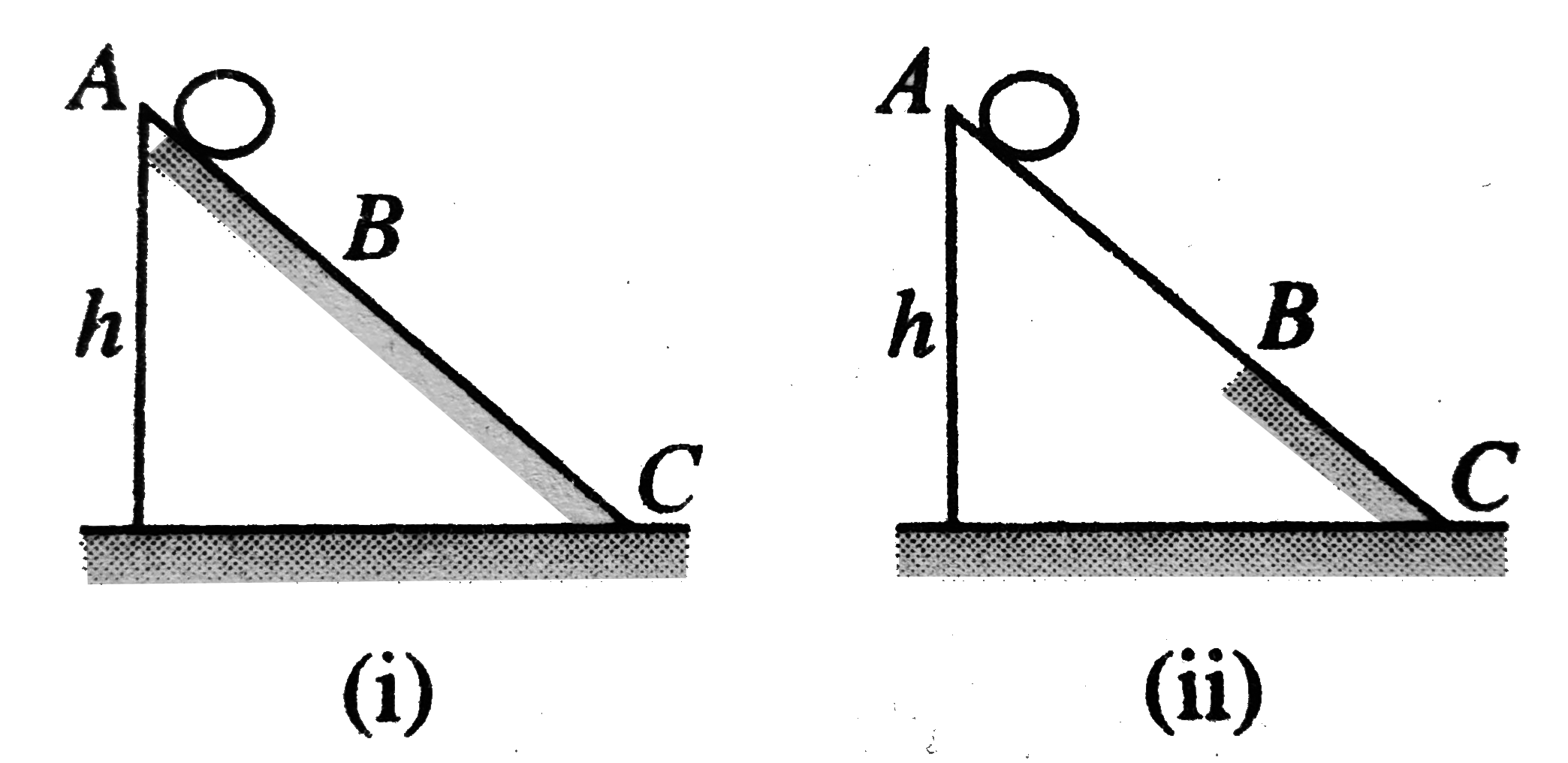
View SolutionIn both the figures all other factors are same, except that in figure (i) `AB` is rough and `BC` is smooth while in figure (ii) `AB` is smooth and `BC` is rough. In figure (i), if a sphere is released from rest it starts rolling. Now consider the figure (ii), if same sphere is A released from top of the inclined plane, what will be the kinetic energy of the sphere on reaching the bottom:
View SolutionA billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity `v_(0).` The angular velocity `omega_(0)` acquired by the ball is
View SolutionA wheel of radius R rolls on the ground with a uniform velocity v. The relative acceleration of topmost point of the wheel with respect to the bottommost point is:
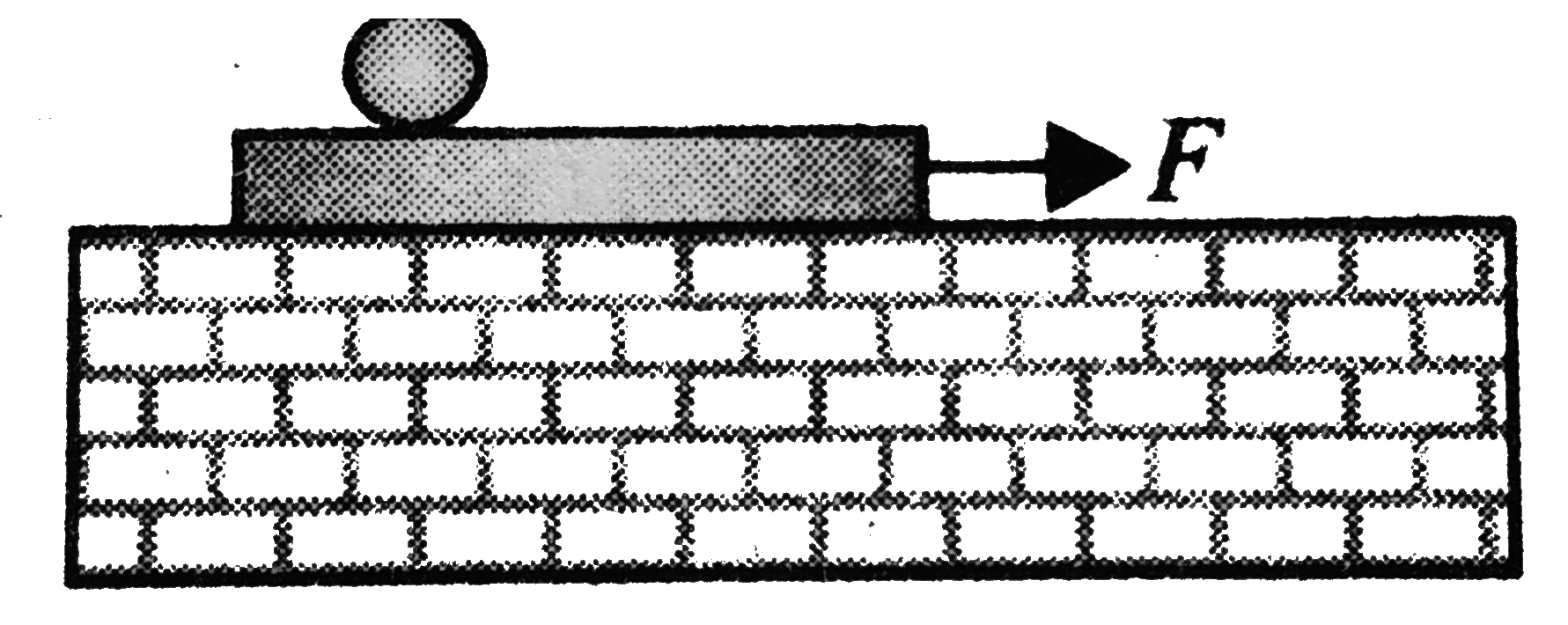
View SolutionA plank with a uniform sphere placed on it resting on a smooth horizontal plane. Plank is pulled to right by a constant force `F`. If sphere does not slip over the plank. Which of the following is incorrect?
View SolutionA rod of length `l` is given two velocities `v_(1)` & `v_(2)` in opposite directions at its two ends at rigt angles to the length. The distance of the instantaneous axis of rotation from `v_(1)` is:
View SolutionTwo particle of equal mass `m` at `A` and `B` are connected by a rigid light rod `AB` lying on a smooth horizontal table. An impulse `J` is applied at `A` in the plane of the table and perpendicular at `AB`. The velocity of particle at `A` is
View Solution
SCQ_TYPE questions and complete solutions for chapter RIGID BODY MOTION of SHREE BALAJI PHYSICS (HINGLISH) of Class 11