Complete Solutions to Basic Maths of chapter BASIC MATHS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | BASIC MATHS |
| ARIHANT MASTER PROBLEM | Basic Maths |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
In an experiment mileage of a car was measured to be `24 kmpl` (Kilometer per liter of fuel consumed). After the experiment it was found that `4 %` of the fuel used during the experiment was leaked through a small hole in the tank. Calculate the actual mileage of the car after the tank was repaired.
View SolutionA man is standing at a distance of 500 m from a building. He notes that angle of elevation of the top of the building is `3.6^(@)`. Find the height of the building. Neglect the height of the man and take `pi = 3.14`
View SolutionA Smuggler in a hindi film is running with a bag `0.3 m xx 0.2 m xx 0.2 m` in dimension. The bag is supposed to be completely filled with gold. Do you think than the director of the film made a technical mistake there ? Density of gold is `19.6 g//c c`.
View SolutionA particle moves along the curve `6y = x^(3)+2`. Find the points on the curve at which the y-coordinate is changing 8 times as fast as the x-coordinate
View SolutionThe area of a regular octagon of side length a is A.
(a) Find the time rate of change of area of the octagon if its side length is being increased at a constant rate of `beta m//s`. Is the time rate of change of area of the octagon constant with time ?
(b) Find the approximate change in area of the octagon as the side length is increased from 2.0 m to 2.001 m.
View SolutionSpirit in a bowl evaporates at a rate that is proportional to the surface area of the liquid. Initially, the height of liquid in the bowl is `H_(0)`. It becomes `(H_(0))/(2)` in time `t_(0)`. How much more time will be needed for the height of liquid to become `(H_(0))/(4)`
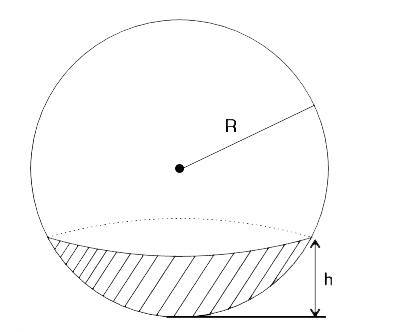
View SolutionShow that the volume of a segment of height h of a sphere of radius R is
`V=(1)/(3)pi h^(2)(3R-h)`
View SolutionThe amount of energy a car expends against air resistance is approximately given by
`E = K ADv^(2)`
where E is measured in Joules. K is a constant, A is the cross-sectional area of the car viewed from the front (in `m^(2)` ), D is the distance traveled (in m), and v is the speed of the car (in m/s). Julie wants to drive from Mumbai to Delhi and get good fuel mileage. For the following questions, assume that the energy loss is due solely to air resistance.
(a) Julie usually drives at a speed of 54 Km/hr. How much more energy will she use if she drives 20% faster ?
(b) Harshit drives a very large SUV car, and Julie drives a small car. Every linear dimension of Harshit's car is double that of Julie's car. Find the ratio of energy spent by Harshit's car to Julie's car when they cover same distance. Speed of Harshit was 10% faster compared to Julie's car.
(c) Write the dimensional formula for K. Will you believe that K depends on density of air?
View SolutionThe volume flow rate `Q ("in m"^(3) s^(-1))` of a liquid through pipe having diameter d is related to viscosity of water `'eta'` (unit Pascal. s) and the pressure gradient along the pipe `(dP)/(dx)` [pressure gradient `(dP)/(dx)` is rate of change of pressure per unit length along the pipe], by a formula of the form
`Q=k eta^(a)d^(b)((dP)/(dx))^(c)`
Where K is a dimensionless constant. Find a,b and c.
View SolutionThe potential energy (U) of a particle can be expressed in certain case as `U=(A^(2))/(2mr^(2))-(BMm)/(r)` Where m and M are mass and r is distance. Find the dimensional formulae for constants.
View SolutionIn the following expression V and g are speed and acceleration respectively. Find the dimensional formulae of a and b
`int (VdV)/(g-bV^(2))=a`
View SolutionThe maximum height of a mountain on earth is limited by the rock flowing under the enormous weight above it. Studies show that maximum height depends on young’s modulus (Y) of the rod, acceleration due to gravity (g) and the density of the rock (d).
(a) Write an equation showing the dependence of maximum height (h) of mountain on Y, g and d. It is given that unit of Y is `Nm^(-2)`.
(b) Take `d = 3 xx 10^(3) kg m^(-3), Y = 1 xx 10^(10) Nm^(-2) and g = 10 ms^(-2)` and assume that maximum height of a mountain on the surface of earth is limited to 10 km [height of mount Everest is nearly 8 km]. Write the formula for h.
View SolutionA particle of mass m is given an initial speed `V_(0)`. It experiences a retarding force that is proportional to the speed of the particle (F = aV). a is a constant.
(a) Write the dimensional formula of constant a.
(b) Using dimensional analysis, derive a formula for stopping time (t) of the particle. Does your formula tell you how 't' depends on initial speed `V_(0)` ? What can you predict about the constant obtained in the formula ?
View SolutionAssume that maximum mass `m_(1)` of a boulder swept along by a river, depends on the speed V of the river, the acceleration due to gravity g, and the density d of the boulder. Calculate the percentage change in maximum mass of the boulder that can be swept by the river, when speed of the river increases by 1%.
View SolutionA massive object in space causes gravitational lensing. Light from a distant source gets deflected by a massive lensing object. This was first observed in 1919 and supported Einstein’s general theory of relativity.
The angle `theta` by which light gets deflected due to a massive body depends on the mass (M) of the body, universal gravitational constant (G), speed of light (c) and the least distance (r) between the lensing object and the apparent path of light. Derive a formula for `theta` using method of dimensions. Make suitable assumptions.
View SolutionThe Casimir effect describes the attraction between two unchanged conducting plates placed parallel to each other in vacuum. The astonishing force ( predicted in 1948 by Hendrik Casimir) per unit area of each plate depends on the planck’s constant (h), speed of light (c) and separation between the plates (r).
(a) Using dimensional analysis prove that the formula for the Casimir force per unit area on the plates is given by `F= k (hc)/(r^(4))` where k is a dimensionless constant
(b) If the force acting on `1xx1` cm plates separated by `1 mu m` is 0.013 dyne, calculate the value of constant k.
View SolutionScattering of light is a process of absorption and prompt re-emission of light by atoms and molecules. Scattering involving particles smaller than wavelength `(lamda)` of light is known as Rayleigh scattering. Let `a_(i)` be amplitude of incident light on a scatterer of volume V. The scattered amplitude at a distance r from the scatterer is `a_(s)`. Assume and `a_(s) alpha a_(i) , a_(s) alpha (1)/(r) and a_(s) alpha V`.
(i) Find the dimensions of the proportionality constant occurring in the expression of `a_(s)`
(ii) Assuming that this constant depends on `lamda`, find the dependence of ratio `(a_(s))/(a_(i))` on `lamda`
(iii) Knowing that intensity of light `I alpha a^(2)` find the dependence of `(I_(s))/(I_(i))` on `lamda`.
View SolutionIt is given that `int (dx)/(1+x^(2))=tan^(-1) x+c` . Using methods of dimensions find `int (dx)/(a^(2)+x^(2))`.
View Solution
Two point sources of light are fixed at the centre (A) and circumference (point B) of a rotating turn table. A photograph of the rotating table is taken. On the photograph a point A and an arc BC appear. The angle `theta` was measured to be `theta = 10.8^(@) pm 0.1^(@)` and the angular speed of the turntable was measured to be `omega = (33.3 pm 0.1)` revolution per minute. Calculate the exposure time of the camera.
View SolutionThe speed (V) of wave on surface of water is given by
`V=sqrt((a lamda)/(2pi)+(2pib)/(rho lamda))`
where `lamda` is the wavelength of the wave and `rho` is density of water. a is a constant and b is a quantity that changes with liquid temperature.
(a) Find the dimensional formulae for a and b.
(b) Surface wave of wavelength 30 mm have a speed of `0.240 ms^(-1)`. If the temperature of water changes by `50^(@)C`, the speed of waves for same wavelength changes to `0.230 ms^(-1)`. Assuming that the density of water remains constant at `1 xx 10^(3) kg m^(-3)`, estimate the change in value of ‘b’ for temperature change of `50^(@)C`.
View SolutionThe line of sight of the brightest star in the sky,
Sirius has a maximum parallax angle of `delta = 0.74 pm 0.02` arc second when observed at six month interval. The distance between two positions of earth (at six - month interval) is `r = 3.000 xx 10^(11) m`
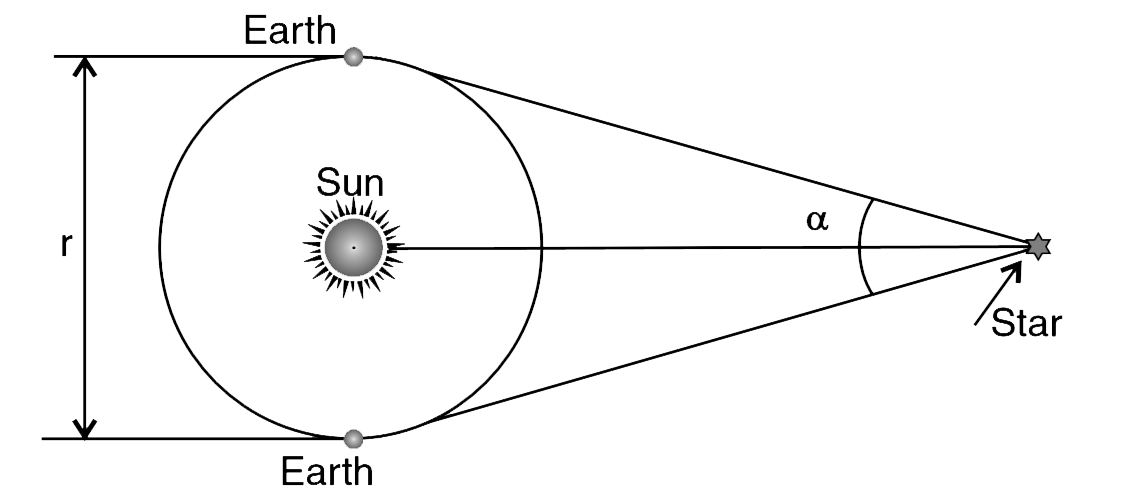
Calculate the distance of Sirius form the Sun with uncertainty, in unit of light year. Given 1 `1y = 9.460 xx 10^(15) m , pi = 3.14`
View SolutionYou inhale about 0.5 liter of air in each breath and breath once in every five seconds. Air has about 1% argon. Mass of each air particle can be assumed to be nearly `5 xx 10^(-26) kg`. Atmosphere can be assumed to be around 20 km thick having a uniform density of `1.2 kg m^(-3)`. Radius of the earth is `R = 6.4 xx 10^(6) m`. Assume that when a person breathes, half of the argon atoms in each breath have never been in that person’s lungs before. Argon atoms remain in atmosphere for long-long time without reacting with any other substance. Given : one year `= 3.2 xx 10^(7)s`
(a) Estimate the number of argon atoms that passed through Newton’s lungs in his 84 years of life.
(b) Estimate the total number of argon atoms in the Earth’s atmosphere.
(c) Assume that the argon atoms breathed by Newton is now mixed uniformly through the atmosphere, estimate the number of argon atoms in each of your breath that were once in Newton’s lungs.
View SolutionA rope is tightly wound along the equator of a large sphere of radius R. The length of the rope is increased by a small amount `l (lt lt R)` and it is pulled away from the surface at a point to make it taut. To what height (h) from the surface will the point rise ?
If the radius of the earth is `R=6400 km and l = 10 mm`, find the value of h. Does the value surprise you.
[For small `theta` take `tan theta=theta +(theta^(3))/(3) and sec theta=1+(theta^(2))/(2). "Also take" (2.3)^((2)/(3))=1.74`]
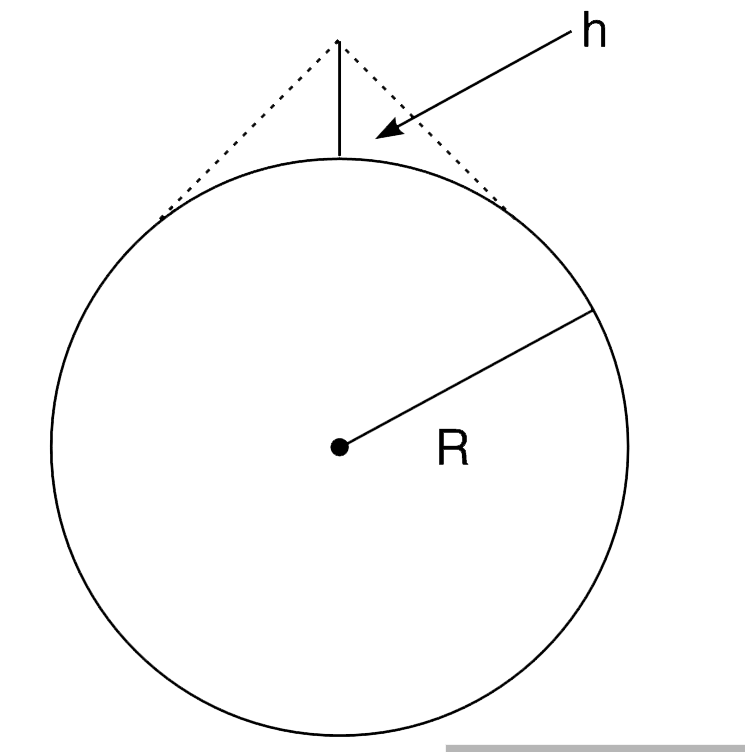
View Solution
Basic Maths questions and complete solutions for chapter BASIC MATHS of ARIHANT PHYSICS (HINGLISH) of Class 11