Complete Solutions to Level 1 of chapter FIRST LAW OF THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FIRST LAW OF THERMODYNAMICS |
| ARIHANT MASTER PROBLEM | Level 1 |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
In different experiments an ideal gas is expanded through
(i) Isothermal
(ii) Adiabatic
(iii) Isobaric process
In which of the processes mentioned the internal energy of the gas may decrease?
View SolutionWhich of the words-out of reversible, irreversible, adiabatic, isothermal, isochoric and isobaric-will you choose to describe the following processes–
(i) A bullet stops in a target [system is bullet plus target].
(ii) A gas, enclosed in a metallic cylinder provided with a piston, is slowly expanded [System is gas]. There is friction between piston and cylinder.
(iii) A piece of hot stone (which has coefficient of thermal expansion equal to zero) is dipped into cold water [System is stone].
View SolutionCalculate the amount of heat required in calorie to change 1 g of ice at `-10^(@)C` to steam at `120^(@)C`. The entire process is carried out at atmospheric pressure. Specific heat of ice and water are `0.5 cal g^(-1) .^(@)C^(-1)` and `1.0 cal g^(-1) .^(@)C^(-1)` respectively. Latent heat of fusion of ice and vaporization of water are `80 cal g^(-1)` and `540 cal g^(-1)` respectively. Assume steam to be an ideal gas with its molecules having 6 degrees of freedom. Gas constant `R = 2 cal mol^(-1) K^(-1)`.
View SolutionA mixture of 1 mole helium and 1 mole nitrogen is enclosed in a vessel of constant volume at 300 K. Find the quantity of heat absorbed by the mixture if the root mean square speed of its molecules get doubled. Give your answer in terms of universal gas constant R.
View SolutionThe average number of degree of freedom per molecule for a gas is 7. A sample of the gas perform 30 J of work when it expands at constant pressure. Find the heat absorbed by the gas in the process.
View SolutionAn ideal gas is made to undergo a process `T = T_(0)e^(alpha V)` where `T_(0)` and `alpha` are constants. Find the molar specific heat capacity of the gas in the process if its molar specific heat capacity at constant volume is `C_(v)`. Express your answer as a function of volume (V).
View SolutionAn ideal diatomic gas undergoes a process in which the pressure is proportional to the volume. Calculate the molar specific heat capacity of the gas for the process.
View Solution(i) A horizontal cylinder is fitted with a smooth movable piston. The cylinder contains an ideal gas. The gas is heated slowly so that the piston gradually moves out. After moving out for some distance the piston encounters an ideal spring and compresses it while moving out. Draw P – V diagram for the entire process.
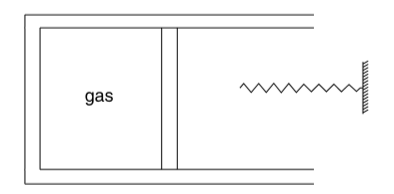
(ii) One mole of an ideal gas is expanded isothermally at temperature `T_(0)` to double its volume from `V_(0)` to `2V_(0)`. Draw a graph showing the variation of volume (V) of the gas versus the amount of heat (Q) added to it.
View SolutionA spherical balloon contains air at pressure `P_(1)` and is placed in vacuum. It has an initial diameter of `D_(1)`. The balloon is heated until its diameter becomes `D_(2) = 2D_(1)`. It is known that pressure in the balloon is proportional to its diameter. Calculate the work done by the gas in expansion.
View Solution(i) An adiabatic cylinder contains an ideal gas. It is fitted with a freely movable insulating piston. In one experiment the piston is pulled out very fast to double the volume of the gas. In another experiment starting from same initial state, the piston is pulled out very slowly to double the volume of the gas. At the end of which experiment the final pressure of the gas will be higher?
(ii) An ideal gas is contained in a cylinder fitted with a movable piston. In an experiment ‘A’ the gas is allowed to perform a work `W (gt 0)` on the surrounding during an isobaric process and thereafter the pressure of the gas is reduced isochorically to half the initial value. At the end of the experiment the temperature of the gas is `T_(A)`. In a different experiment ‘B’ the pressure of the gas is reduced to half in an isochoric process and then the gas performs a work W on the surrounding during an isobaric process. At the end of the experiment the gas temperature is `T_(B)`. Which is higher, `T_(A)` or `T_(B)`?
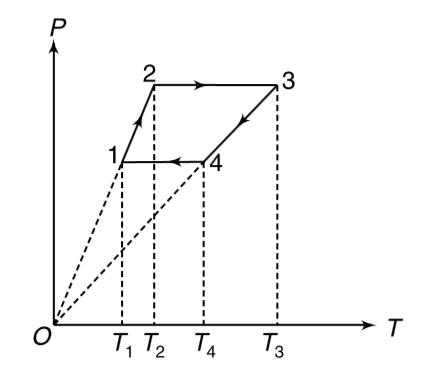
View Solutionn moles of an ideal gas is taken through a four step cyclic process as shown in the diagram. Calculate work done by the gas in a cycle in terms of temperatures `T_(1), T_(2), T_(3)` and `T_(4)`
View SolutionTwo thermally insulated vessels are filled with an ideal gas. The pressure, volume and temperature in the two vessels are `P_(1), V_(1), T_(1)` and `P_(2), V_(2), T_(2)` respectively. Now, the two vessels are connected using a short insulating tube.
(a) Find final temperature of the gas.
(b) Express the final pressure of the gas in terms of `P_(1), V_(1), P_(2)` and `V_(2)` only.
View SolutionTwo tanks are connected by a valve. One tank contains 2 kg of an ideal gas at `77^(@)C` and 0.7 atm pressure. The other tank has 8kg of same gas at `27^(@)C` and 1.2 atm pressure. The valve is opened and the gases are allowed to mix. The final equilibrium temperature was found to be `42^(@)C`.
(a) Find the equilibrium pressure in both tanks.
(b) How much heat was transferred from surrounding to the tanks during the mixing process. Given: `C_(v)` for the gas is `0.745 KJ kg^(-1) K^(-1)`.
View SolutionThe ratio of specific heats (`C_(p)` and `C_(v)`) for an ideal gas is `gamma`. Volume of one mole sample of the gas is varied according to the law `V = (a)/(T^(2))` where T is temperature and a is a constant. Find the heat absorbed by the gas if its temperature changes by `Delta T`.
View SolutionA sample of an ideal gas has diatomic molecules at a temperature at which effective degree of freedom is 5. Under the action of a suitable radiation the molecules split into two atoms. The ratio of the number of dissociated molecules to the total number of molecules is a. Plot the ratio of molar specific heats `gamma (=(C_(p))/(C_(v)))` as a function of `alpha`.
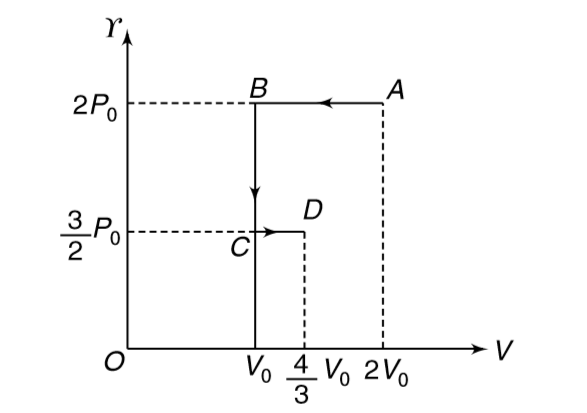
View SolutionAn ideal gas undergoes a series of processes represented by`a rarr B rarr C rarr D` on the P-V diagram. Answer the following questions.
(a) Is the internal energy of the gas at B and D equal?
(b) Find work done by the gas in the process A rarr B rarr C rarr D`.
(c) Is it right to say that point B and D lie on an isotherm?
(d) Find the ratio of internal energy of the gas in state A to that in state D.
View Solution30 people gather in a 1`0 m xx 5 m xx 3 m` room for a confidential meeting. The room is completely sealed off and insulated. Calculate the rise in temperature of the room in half an hour. Assume that average energy thrown off by the body of a person is 2500 kcal/day, density of air is `1.2 kg/m^(3)` and specific heat specify capacity of air at constant volume is `0.24 k cal kg^(-1) . ^(@)C^(-1)`. Neglect volume occupied by human bodies.
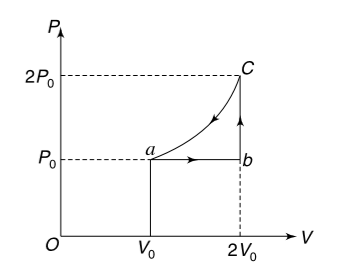
View SolutionOne mole of an ideal monoatomic gas is taken through a cycle a-b-c-a as shown in figure. Find the difference in maximum and minimum value of internal energy of the gas during the cycle
View SolutionAn ideal mono atomic gas A is supplied heat so as to expand without changing its temperature. In another process, starting with the same state, it is supplied heat at constant pressure. In both the cases a graph of work done by the gas (W) is plotted versus heat added (Q) to the gas. The ratio of slope of the graphs obtained in first and second process is `eta_(1)`. The same ratio obtained for an ideal diatomic gas in `eta_(2)`. Find the ratio `(eta_(1))/(eta_(2))`.
View SolutionFor an ideal gas the ratio of specific heats is `(C_(p))/(C_(v)) = gamma`. The gas undergoes a polytropic process PV^(n) =` a constant. Find the values of n for which the temperature of the gas increases when it rejects heat to the surrounding.
View SolutionFor an ideal gas the slope of V-T graph during an adiabatic process is (dV)/(dT) = -m` at a point where volume and temperature are `V_(0)` and `T_(0)`. Find the value of `C_(p)` of the gas. It is given that m is a positive number.
View SolutionA gas undergoes a cyclic process a-b-c-a which is as shown in the PV diagram. The process a-b is isothermal, b-c is adiabatic and c-a is a straight line on P-V diagram. Work done in process ab and bc is 5 J and 4 J respectively. Calculate the efficiency of the cycle, if the area enclosed by the diagram abca in the figure is 3 J.

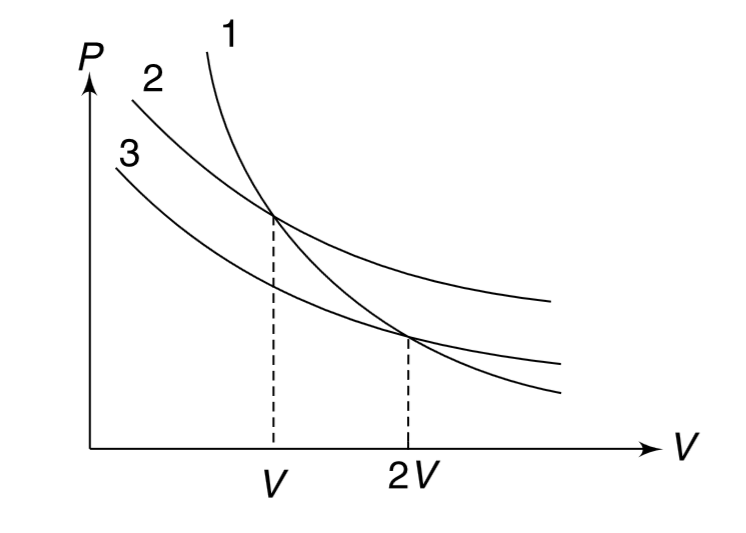
View SolutionIn the shown figure curve 1 represents an adiabat for n moles of an ideal mono atomic gas. Curve 2 and 3 are two isotherms for the same sample of the gas. Calculate the ratio of work done by the gas in doubling its volume from V to 2V along the isotherms 2 and 3.
View SolutionA mass less piston divides a thermally insulated cylinder into two parts having volumes V = 2.5 litre and 3 V = 7.5 litre. 0.1 mole of an ideal gas is confined into the part with volume V at a pressure of `P = 10^(5) N//m^(2)`. The other part of the cylinder is empty. The piston is now released and the gas expands to occupy the entire volume of the cylinder. Now the piston is pressed back to its initial position. Find final temperature of the gas.
[Take `R = (25)/(3) J mol^(-1) K^(-1)` and `gamma = 1.5` for the gas]
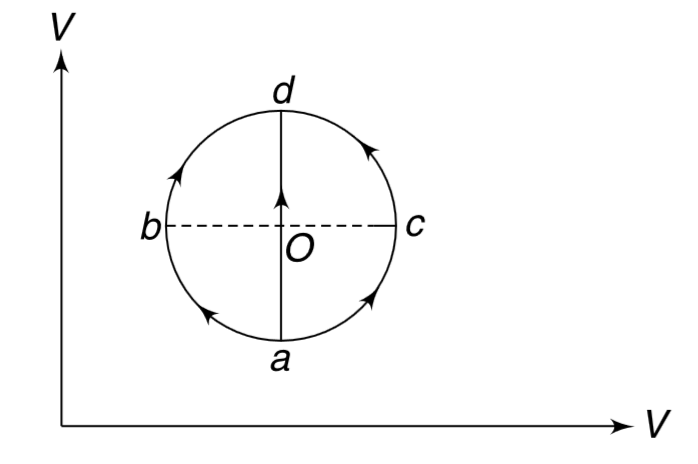
View SolutionAn ideal gas is taken from its initial state a to its find state d in three different quasi static processes marked as a – b – d, a – o – d and a – c – d. Rank the net heat absorbed by the gas in the three processes. The diagram shown is a circle with centre at o.
View SolutionThe figure shows a Carnot cycle for an ideal gas on a P-V diagram. Which of the areas `A_(1)` or `A_(2)` is larger?

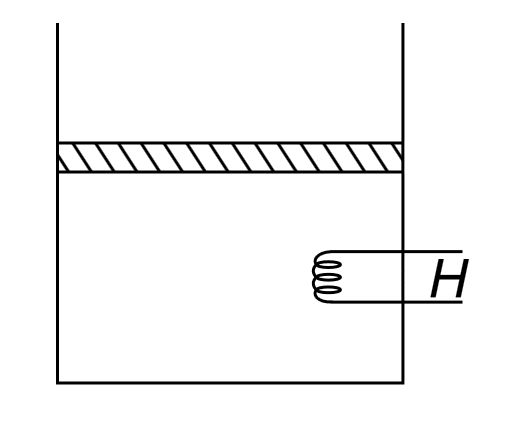
View SolutionAir is contained in a vertical piston – cylinder assembly fitted with an electric heater. The piston has a mass of 50 kg and cross sectional area of `0.1 m^(2)`. Mass of the air inside the cylinder is 0.3 kg. The heater is switched on and the volume of the air slowly increases by `0.045 m^(3)`. It was found that the internal energy of the air increased by `32.2 kJ//kg` and that of the piston increased by 0.06 kJ/kg. Assume that the container walls and outer surface of the piston are well insulated and there is no friction. The atmospheric pressure is 100 kPa. Determine the heat transferred by the heater to the system consisting of air and the piston.
View SolutionOne mole of an ideal mono atomic gas is at a temperature `T_(0) = 1000 K` and its pressure is `P_(0)`. The gas is adiabatically cooled so that its pressure becomes `(2)/(3) P_(0)`. Thereafter, the gas is cooled at constant volume to reduce its pressure to `(P_(0))/(3)` . Calculate the total heat absorbed by the gas during the process.
Take `R = (25)/(3)J mol^(-1)K^(-1)` and `((2)/(3))^(2//5) = 0.85`
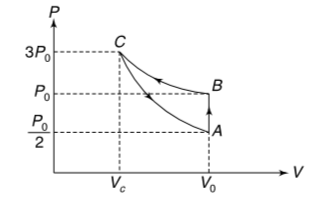
View SolutionOne mole of an ideal gas is carried through a thermodynamics cycle as shown in the figure. The cycle consists of an isochoric, an isothermal and an adiabatic process. Find the adiabatic exponent of the gas.
View SolutionOne mole of an ideal gas is taken along the process in which `PV^x = ` constant. The graph shown represents the variation of molar heat capacity of such a gas with respect to `x`. The value of `c'` and `x'` respectively, are given by
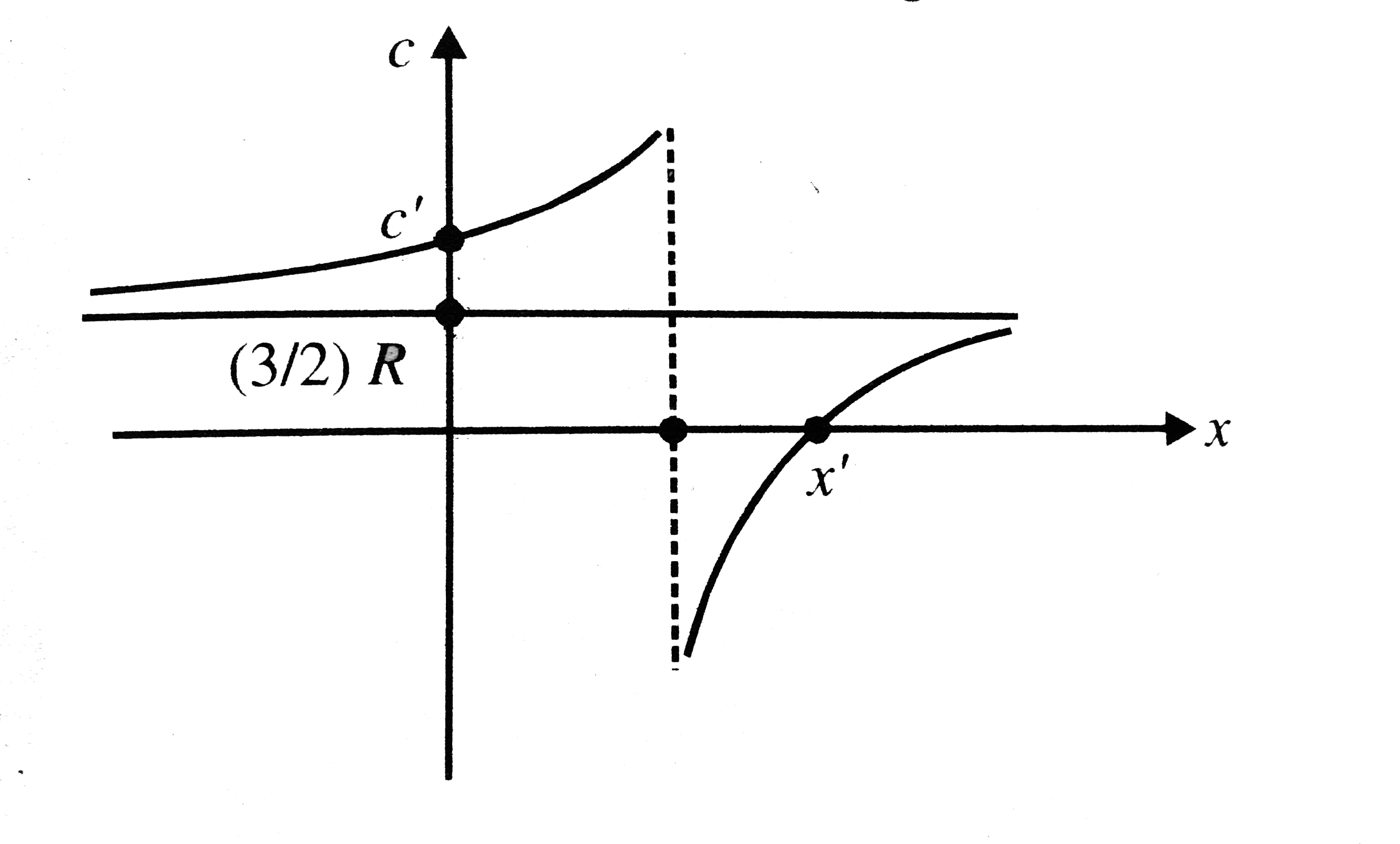
View Solution
Level 1 questions and complete solutions for chapter FIRST LAW OF THERMODYNAMICS of ARIHANT PHYSICS (HINGLISH) of Class 11