Complete Solutions to All Questions of chapter WORK, POWER AND ENERGY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, POWER AND ENERGY |
| ARIHANT MASTER PROBLEM | All Questions |
| Number Of Questions | 80 |
| Academic Year | 2023-24 |
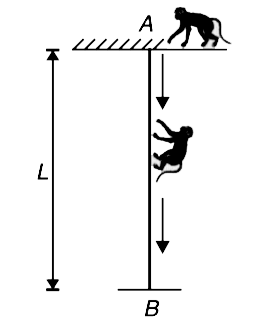
(i) The cause of increases in kinetic energy when a man starts running without his feet slipping on ground is asked to two students. Their answers are– Harshit: Cause of increase in kinetic energy is work done by friction force. Without friction the man cannot run. Akanksha: Cause of increase in kinetic energy is work done by internal (muscle) forces of the body. Who is right? (ii) An inextensible rope is hanging from a tree. A monkey, having mass m, climbs to a height h grabbing the rope tightly. The monkey starts from rest and ends up hanging motionlessly on the rope at height h. (a) How much work is done by gravity on the monkey? (b) How much work is done by the rope on the monkey? (c) Using work – energy theorem, explain the increase in mechanical energy of the monkey.
View SolutionA man of mass M jumps from rest, straight up, from a flat concrete surface. Centre of mass of the man rises a distance h at the highest point of the motion. Find the work done by the normal contact force (between the man’s feet and the concrete floor) on the man.
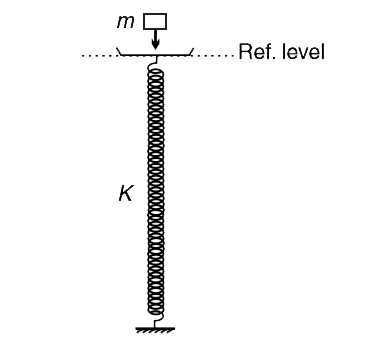
View SolutionA block of mass m = 10 kg is released from the top of the smooth inclined surface of a wedge which is moving horizontally toward right at a constant velocity of u = 10 m/s. Inclination of the wedge is `theta=37^(@)`. Calculate the work done by the force applied by the wedge on the block in two seconds in a reference frame attached to -
 (a) the ground (b) the wedge.
(a) the ground (b) the wedge.
[Take `g=10 m//s^(2)`]
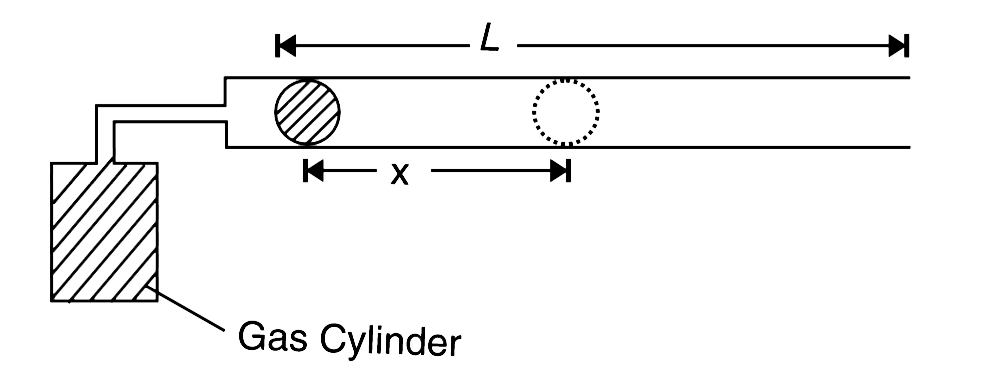
View SolutionIn an industrial gun, when the trigger is pulled a gas under pressure is released into the barrel behind a ball of mass m. The ball slides smoothly inside the barrel and the force exerted by the gas on the ball varies as
`F=F_(0)(1-x/L)` Where L is length of the end of the barrel from the initial position of the ball and x is instantaneous displacement of the ball from its initial position. Neglect any other force on the ball apart from that applied by the gas. Calculate the speed (V) of the ball with which it comes out of the gun.
View SolutionA particle of mass 3 kg takes 2 second to move from point A to B under the action of gravity and another constant force `vec(F)=(12hati-3hatj+12 hatk) N`, where the unit vector `hatk` is in the direction of upward vertical. The position vector of point B is `vec(r)_(B)=(15 hati-7hatj-6hatk)m` and velocity of the particle when it reaches B is `vec(V)_(B)=(12hati+hatj-4hatk m//s`.
(a) Find the velocity, `vec(V)_(A)`of the particle when it was at A.
(b) Find position vector, `vec(r)_(A)` of point A
(c) Find work done by the force `vec(F)` as the particle moves from A to B
(d) Find change in gravitational potential energy of the particle is it moves from A to B
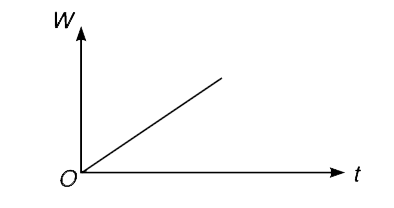
View SolutionA particle can move along a straight line. It is at rest when a force (F) starts acting on it directed along the line. Work done by the force on the particle changes with time(t) according to the graph shown in the fig. Can you say that the force acting on the particle remains constant with time?
View SolutionA particle is moving on a straight line and all the forces acting on it produce a constant power P calculate the distance travelled by the particle in the interval its speed increase from V to 2V.
View SolutionWork done and power spent by the motor of an escalator are W and P respectively when it carries a standing passenger from ground floor to the first floor. Will the work and power expended by the motor change if the passenger on moving escalator walks up the staircase at a constant speed?
View Solution(i) A block is connected to an ideal spring on a horizontal frictionless surface. The block is pulled a short distance and released. Plot the variation of kinetic energy of the block vs the spring potential energy.
(ii) A ball of mass 200 g is projected from the top of a building 20 m high. The projection speed is 10 m/s at an angle `theta=sin^(-1)(3/5)` from the horizontal. Sketch a graph of kinetic energy of the ball against height measured from the ground. Indicate the values of kinetic energy at the top and bottom of the building and at the highest point of the trajectory, specifying the heights on the graph. Neglect air resistance and take `g = 10 m//s^(2)`
View SolutionA car of mass m 1600 kg, while moving on any road, experience resistance to its motion given by `(m+nV^(2))` newton, where m and n are positive constants. On a horizontal road the car moved at a constant speed of 40 m/s when the engine developed a power of 53 KW. When the engine developed an output of 2 KW the car was able to travel on a horizontal road at a constant speed of 10 m/s. (a) Find the power that the engine must deliver for the car to travel at a constant speed of 40 m/s on a horizontal road. (b) The car is able to climb a hill at a constant speed of 40 m/s with its engine working at a constant rate of 69 KW. Calculate the inclination of the hill (in degree)
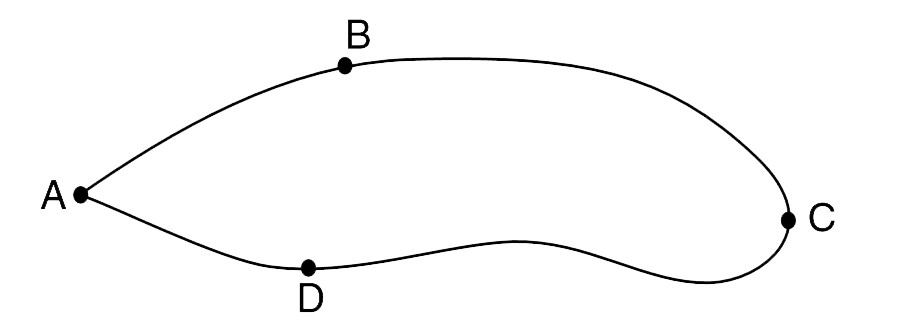
View SolutionA particle moves along the loop A–B–C–D–A while a conservative force acts on it. Work done by the force along the various sections of the path are `-W_(AtoB)=-50 J, W_(BtoC) =25 J, W_(CtoD)=60 J`. Assume that potential energy of the particle is zero at A. Write the potential energy of particle when it is at B and D.
View SolutionA moving particle of mass m is acted upon by five forces` vec(F)_(1),vec(F)_(2),vec_(F)_(3),vec(F)_(4)` and `vec(F)_(5`. Forces `vec(F)_(2)` and `vec(F)_(3)` are conservative and their potential energy functions are U and W respectively. Speed of the particle changes from `V_(a)` to `V_b` when it moves from position a to b. Which of the following statement is/are true – (a) Sum of work done by `vec(F)_(1),vec(F)_(4)` and `vec(F)_(5)=U_(b)-U_(a)+W_(b)-W_(a)`
(b) Sum of work done by `vec(F)_(1),vec(F)_(4)` and `vec(F)_(5)=U_(b)-U_(a)+W_(b)-W_(a)+1/2m(V_(a)^(2)-V_(a)^(2))`
(c) Sum of work done by all five forces `=1/2m(V_(b)^(2)-V_(a)^(2))`
(d) Sum of work done by `vec(F)_(2)` and `vec(F)_(3)=(U_(b)+W_(b))-(U_(a)+W_(a))`
View Solution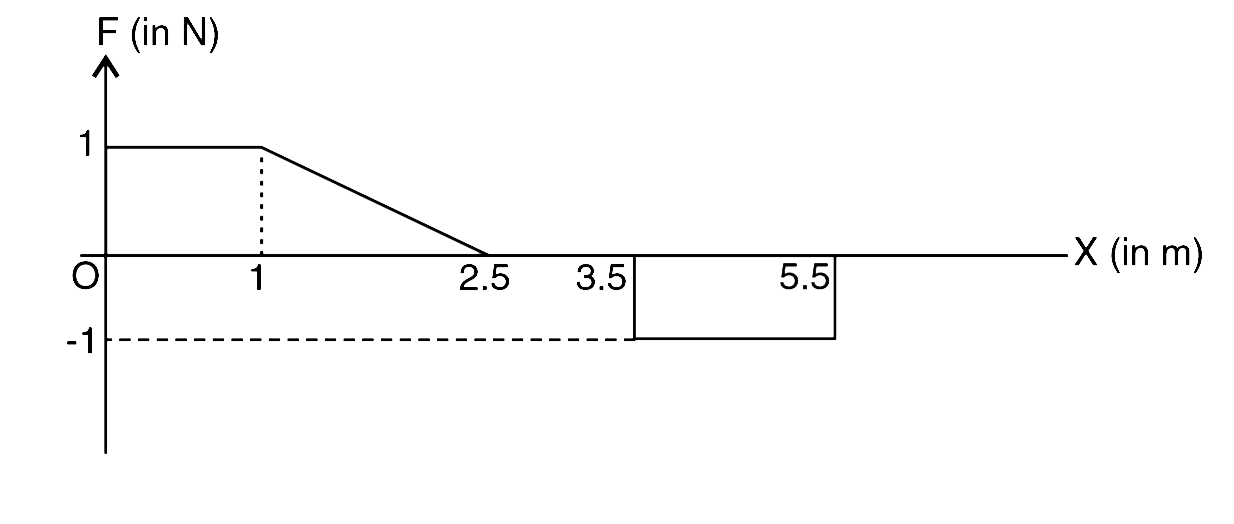
The given graph represents the total force in x direction being applied on a particle of mass m = 2 kg that is constrained to move along x axis. What is the minimum possible speed of the particle when it was at x = 0?
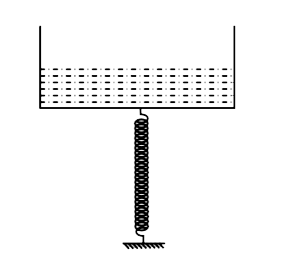
View SolutionA vertical spring supports a beaker containing some water in it. Water slowly evaporates and the compression in the spring decreases. Where does the elastic potential energy stored in the spring go?
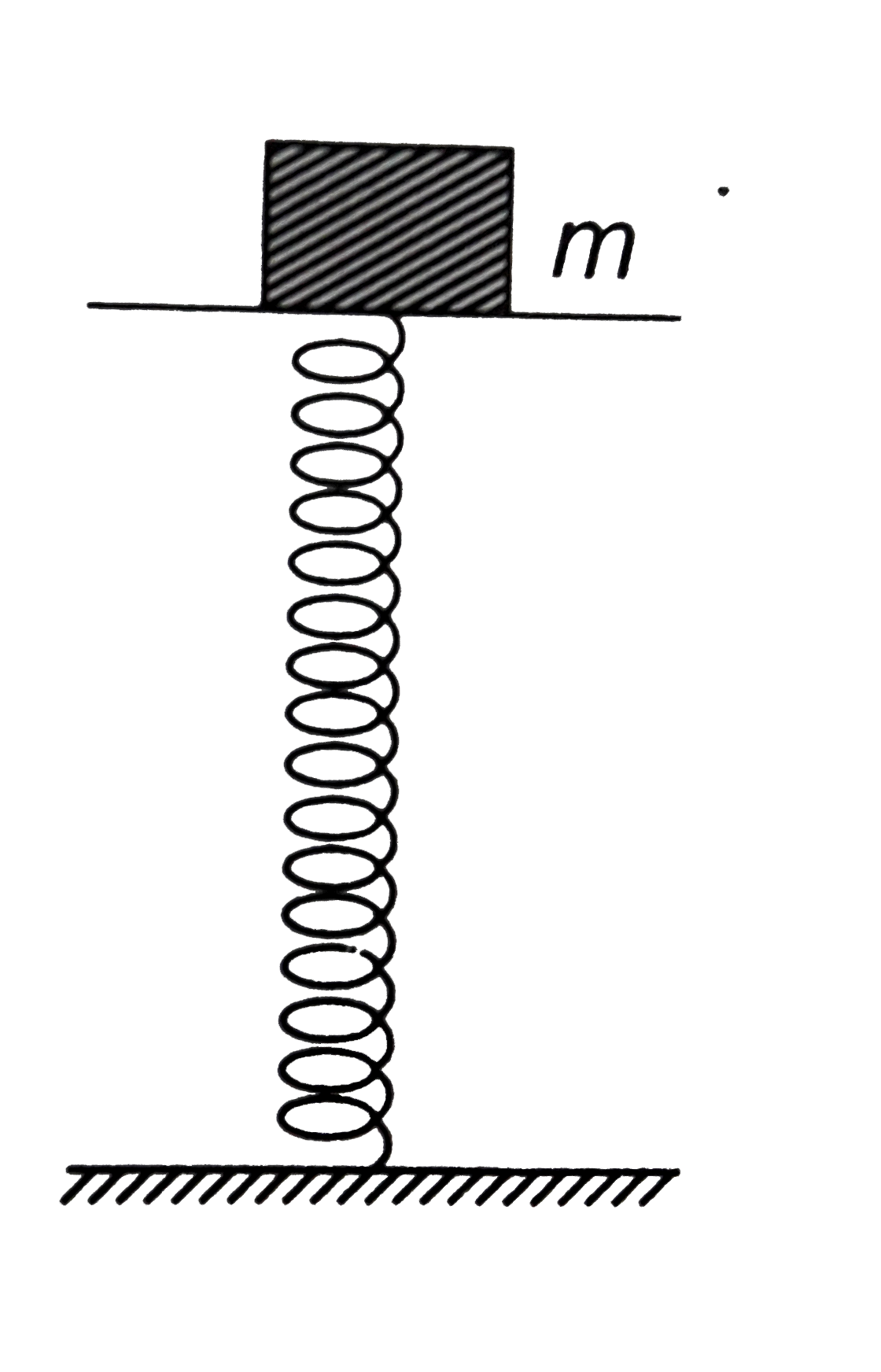
View SolutionA mass of `2.0 kg` is put on a flat pan attached to a vertical spring fixed on the ground as shown in figure. The mass of the spring and the pan is negligible. When pressed slightly and realeased the mass executes a simple contant is `200 N//m`. What should be the minimum amplitude of the motion, so that the mass gets the detached from the pan? `(Take g= 10 m//s^(2))`
View SolutionA snake of mass M and length L is lying on an incline of inclination `30^(@)`. It craws up slowly and overhangs half its length vertically. Assume that the mass is distributed uniformly along the length of the snake and its hanging part as well as the part on the incline both remain straight.
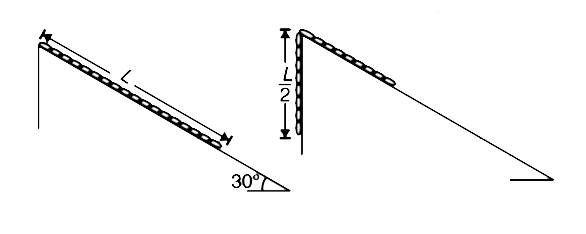
(a) Find the work done by the snake against gravity (Wg) (b) Will the answer to part (a) be different if the snake were of half the length but of same mass.
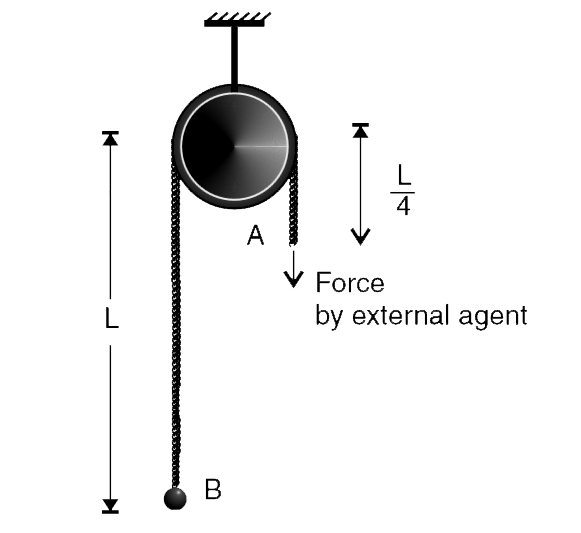
View SolutionA uniform rope of linear mass density `lambda` (kg/m) passes over a smooth pulley of negligible dimension. At one end B of the rope there is a small particle having mass one fifty of the rope. Initially the system is held at rest with length L of the rope on one side and length `L/4` on the other side of the pulley (see fig). The external agent begins to pull the end A downward. Find the minimum work that the agent must perform so that the small particle will definitely reach the pulley.
View SolutionA particle of mass m = 100 g is projected vertically up with a kinetic energy of 20 J form a position where its gravitational potential energy is – 50 J. Find the maximum height to which the particle will rise above its point of projection. [`g = 10 m//s^2`]
View SolutionA physics student writes the elastic potential energy stored in a spring as `U=1/2KL^(2)+1/2Kx^(2),` where L is the natural length of the spring, x is extension or compression in it and K is its force constant. A block of mass M travelling with speed V hits the spring and compresses it.
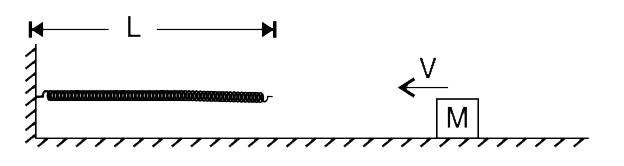
Find the maximum compression caused.
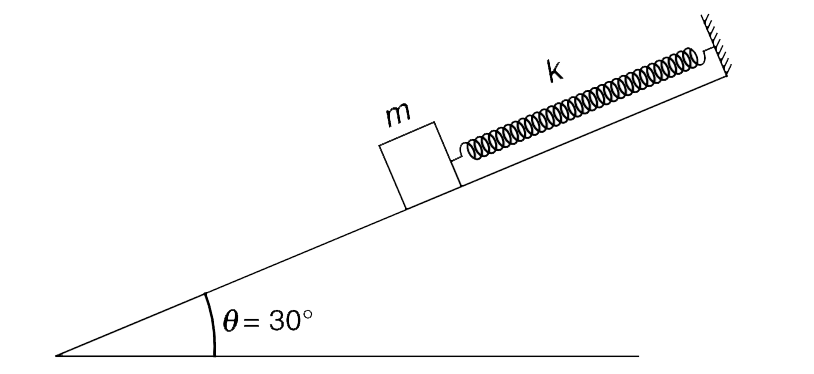
View SolutionA block of mass m = 4 kg is kept on an incline connected to a spring (see fig). The angle of the incline is `theta = 30^(@)` and the spring constant is K = 80 N/m. There is a very small friction between the block and the incline. The block is released with spring in natural length. Find the work done by the friction on the block till the block finally comes to rest.[`g = 10 m//s^2`]
View SolutionA body is projected directly up a plane which is inclined at an angle `theta` to the horizontal. It was found that when it returns to the starting point its speed is half its initial speed. (a) Was dissipation of mechanical energy of the body, due to friction, higher during ascent or descent? (b) Calculate the coefficient of friction (`mu`) between the body and the incline.
View SolutionA tanker filled with water starts at rest and then rolls, without any energy loss to friction, down a valley. Initial height of the tanker is `h_1`. The tanker, after coming down, climbs on the other side of the valley up to a height `h_2`. Throughout the journey, water leaks from the bottom of the tanker. How does `h_2` compare with `h_1`?
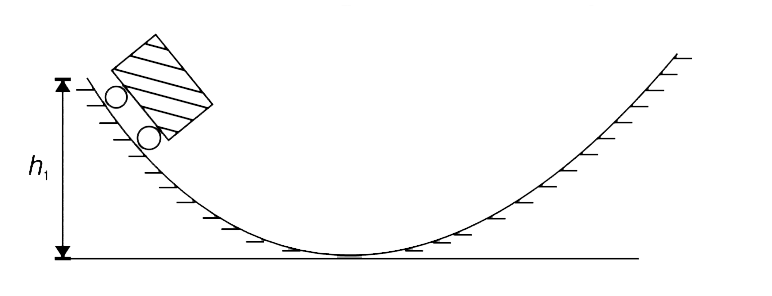
View SolutionA stone with weight W is thrown vertically upward into air with initial speed u. Due to air friction a constant force R acts on the stone, throughout its flight. Find – (a) the maximum height reached and (b) speed of stone on reaching the ground.
View SolutionA mass m = 0.1 kg is attached to the end B of an elastic string AB with stiffness k = 16 N/m and natural length `l_0 = 0.25 m`. The end A of the string is fixed. The mass is pulled down so that AB is `2l_0` = 0.5 m and then released. (a) Find the velocity of the mass when the string gets slack for the first time.
(b) At what distance from A the mass will come to rest for the first time after being released.

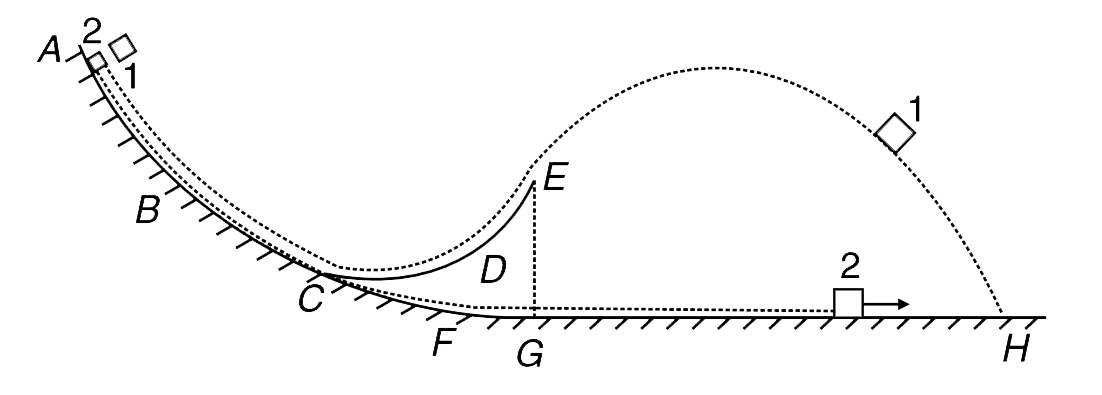
View SolutionTwo blocks 1 and 2 start from same point A on a smooth slide at the same time. The track from A to B to C is common for the two blocks. At C the track divides into two parts. Block 1 takes the route C–D–E and gets airborne after E. Block 2 moves along CFGH. Point E is vertically above G and the stretch GH is horizontal. Block 1 lands at point H. (a) Where is the other block at the time block 1 lands at H? Has it already crossed H or yet to reach there? (b) Which block will reach at H with higher speed ?
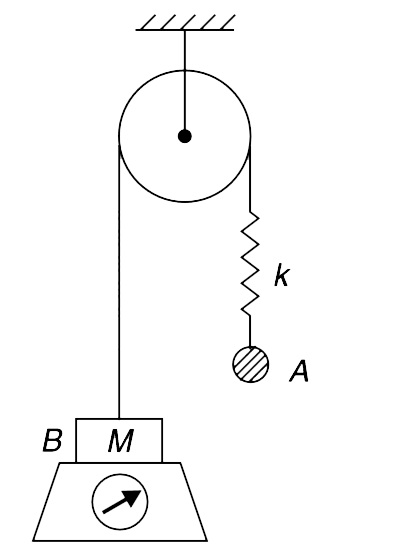
View SolutionIn the arrangement shown in the figure, block B of mass M rests on a weighing scale. Ball A is released from a position where spring is in its natural length and the scale shows the correct weight of block B. Find the mass of ball A so that the minimum reading shown by the scale subsequently is half the true weight of B.
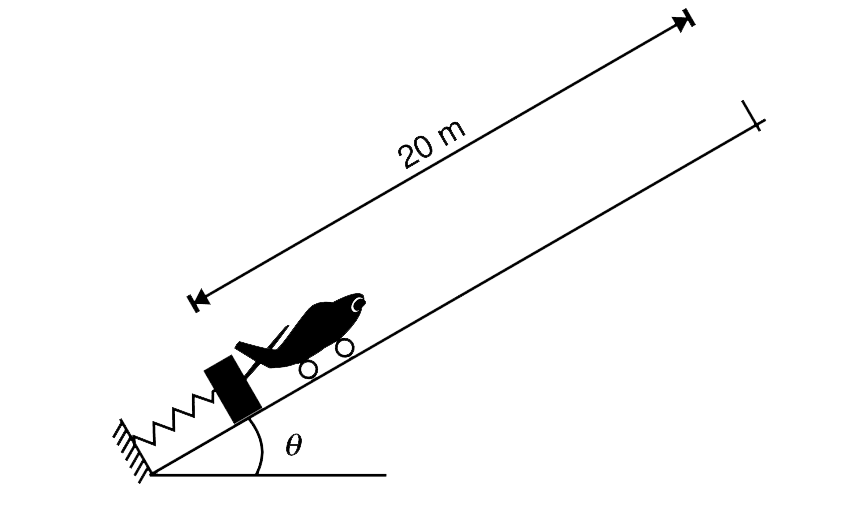
View SolutionIn an aircraft carrier warship the runway is a 20 m long strip inclined at `theta = 20^(@)` to the horizontal. The launcher is effectively a large spring that pushes an aircraft of mass m = 2000 kg for first 5 m of the 20 m long runway. The jet engine of the plane produces a constant thrust of `6 xx 10^(4) N` for the entire length of the runway. The plane needs to have a speed of 180 kph at the end of the runway. Neglect air resistance and calculate the spring constant of the launcher. [`sin 20^(@) = 0.3` and `g = 10 m//s^(2)`]
View SolutionA block of mass M is placed on a horizontal surface having coefficient of friction m. A constant pulling force `F=(Mg)/2` is applied on the block to displace it horizontally through a distance d. Find the maximum possible kinetic energy acquired by the block.
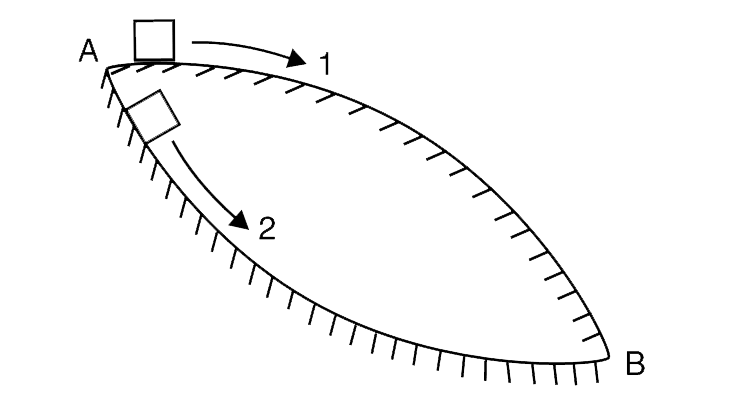
View SolutionA small block is made to slide, starting from rest, along two equally rough circular surfaces from A to B through path 1 and 2. The two paths have equal radii. The speed of the block at the end of the slide was found to be `V_1` and `V_2` for path 1 and 2 respectively. Which one is larger `V_1` or `V_2`?
View SolutionA particle can move along x axis under influence of a conservative force. The potential energy of the particle is given by `U = 5x^2 – 20x + 2` joule where x is co-ordinate of the particle expressed in meter. The particle is released at x = –3 m (a) Find the maximum kinetic energy of the particle during subsequent motion. (b) Find the maximum x co-ordinate of the particle.
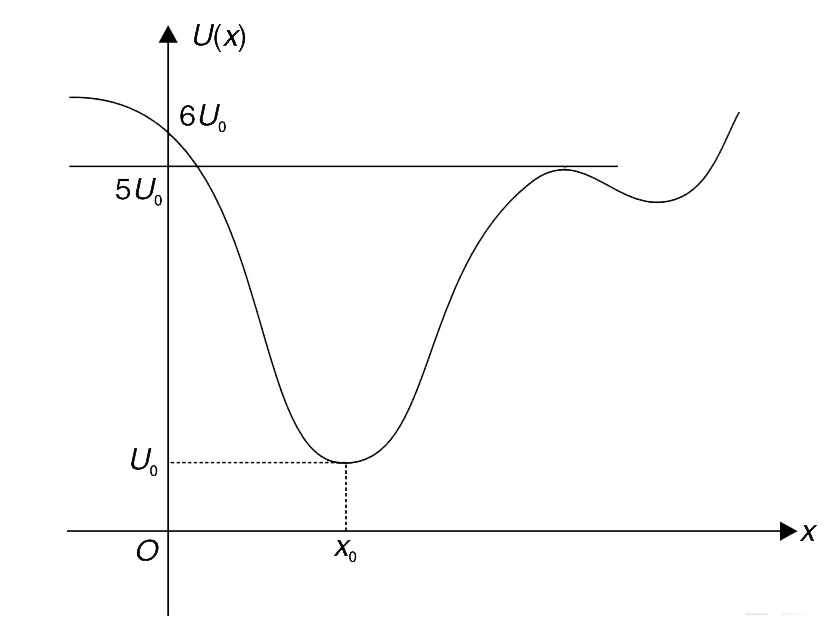
View SolutionA particle is constrained to move along x axis under the action of a conservative force. The potential energy of the particle varies with position x as shown in the figure. When the particle is at x = x0, it is given a kinetic energy (k) such that 0 lt k lt 4U0 (a) Does the particle ever reach the origin? (b) Qualitatively describe the motion of the particle
View SolutionA pillar having square cross section of side length L is fixed on a smooth floor. A particle of mass m is connected to a corner A of the pillar using an inextensible string of length 3.5 L. With the string just taut along the line BA, the particle is given a velocity v perpendicular to the string. The particle slides on the smooth floor and the string wraps around the pillar.
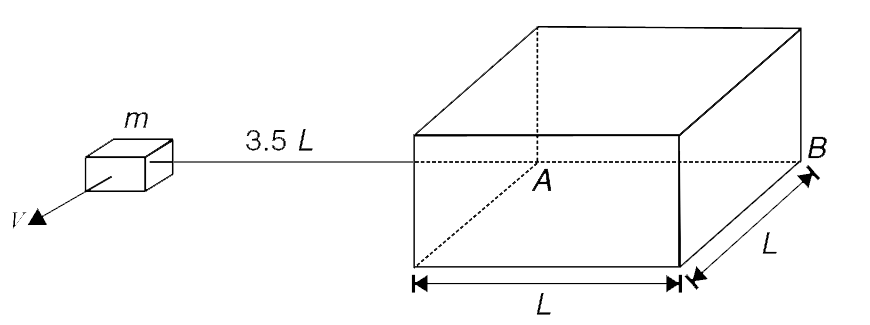
(a) Find the time in which the particle will hit the pillar. (b) Find the tension in the string just before the particle hits the pillar. Neglect any energy loss of the particle.
View Solution(i) A simple pendulum consist of a small bob of mass m tied to a string of length L. Show that the total energy of oscillation of the pendulum is `E~=1/2 mg L theta_(0)^(2)` when it is oscillating with a small angular amplitude `theta_(0)`. Assume the gravitational potential energy to be zero of the lowest position of the bob. (ii) Three identical pendulums A, B and C are suspended from the ceiling of a room. They are swinging in semicircular arcs in vertical planes. The string of pendulum A snaps when it is vertical and it was found that the bob fell on the floor with speed `V_1`. The string of B breaks when it makes an angle of 30° to the vertical and the bob hits the floor with speed `V_2`. The string of pendulum C was cut when it was horizontal and the bob falls to the floor hitting it with a speed V3. Which is greatest and which is smallest among `V_1,V_2` and `V_3`?
View SolutionAB is a mass less rigid rod of length 2l. It is free to rotate in vertical plane about a horizontal axis passing through its end A. Equal point masses (m each) are stuck at the centre C and end Bof the rod. The rod is released from horizontal position. Write the tension in the rod when it becomes vertical.

View SolutionA particle of mass m is suspended by a string of length l from a fixed rigid support. Particle is imparted a horizontal velocity `u=sqrt(2gl)`. Find the angle made by the string with the vertical when the acceleration of the particle is inclined to the string by `45^(@)`?
View SolutionA particle of mass m is moving in a circular path of constant radius r such that its centripetal acceleration ac is varying with time t as `a_c = k^2rt^2`, where k is a constant. Calculate the power delivered to the particle by the force acting on it.
View SolutionA ball suspended by a thread swing in a vertical plane that its acceleration values in the lowest possition and the extreme postition are equal . Find the thread deffection angle in the extreme possition.
View SolutionA particle of mass `m` oscillates inside the smooth surface a fixed pipe of radius `R`. The axis of the pipe is horizontal and the particle moves from `B` to `A` and back. At an instant the kinetic energy of the particle is `K` (say at position of the particle shown in figure ). Then choose the correct value of force applied by particle on the pipe at this instant.
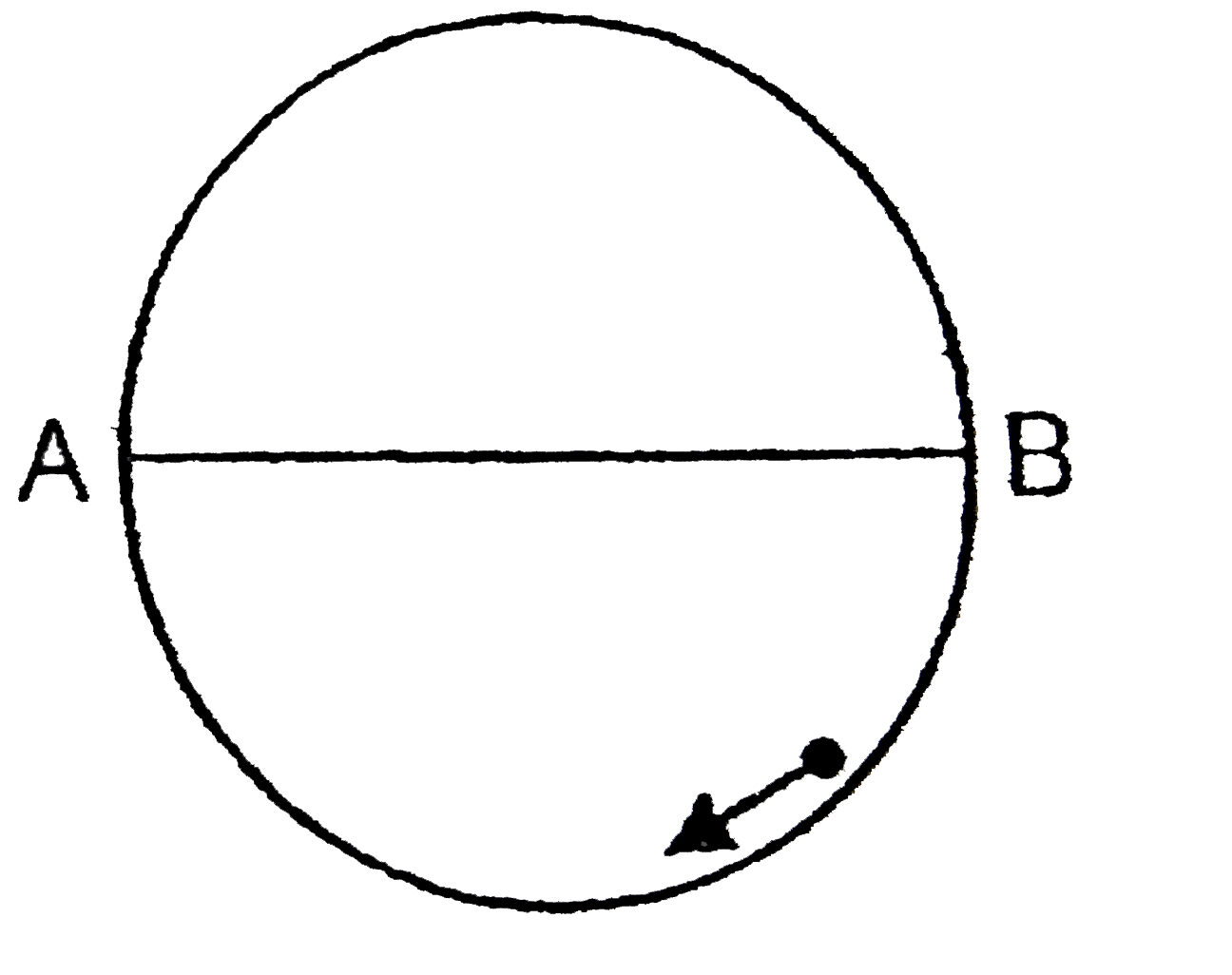
View Solution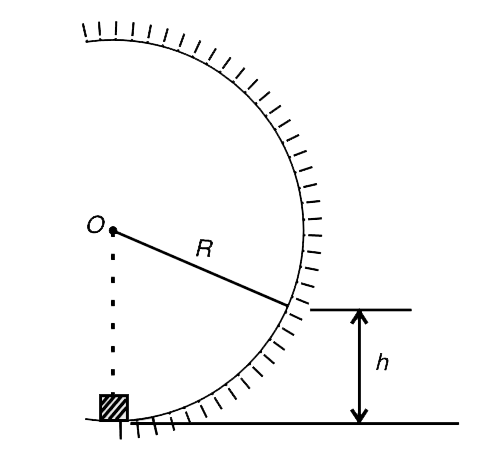
(i) There is a vertical loop of radius R. A small block of mass m is slowly pushed along the loop from bottom to a point at height h. Find the work done by the external agent if the coefficient of friction is `mu`. Assume that the external agent pushes tangentially along the path. (ii) A block of mass m slides down a smooth slope of height h, starting from rest. The lower part of the track is horizontal. In the beginning the block has potential energy U = mgh which gets converted into kinetic energy at the bottom. The velocity at bottom is `v=sqrt(2gh)`. Now assume that an observer moving horizontally with velocity `v=sqrt(2gh)` towards right observes the sliding block. She finds that initial energy of the block is `E=mgh+1/2 mv^(2)` and the final energy of the block when it reaches the bottom of the track is zero. Where did the energy disappear?

View SolutionA completely filled cylinderical tank of height H contains water of mass M. At a height h above the top of the tank there is another wide container. The entire water from the tank is to be transferred into the container in time `t_0` such that level of water in tank decreases at a uniform rate. How will the power of the external agent vary with time?
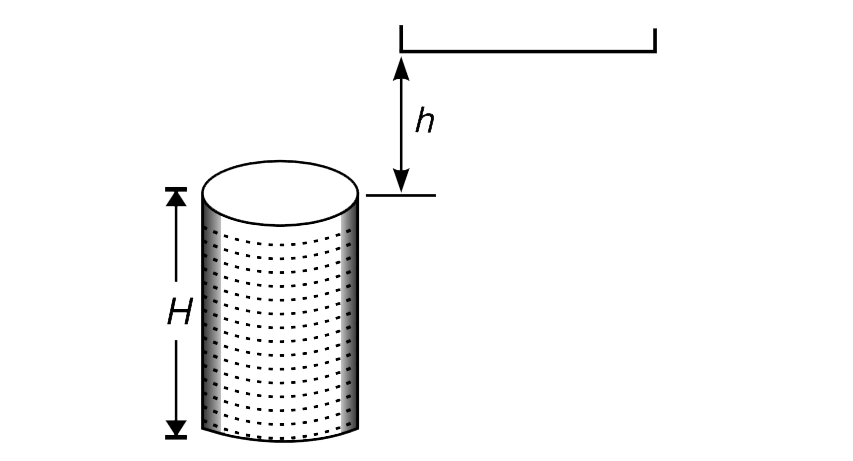
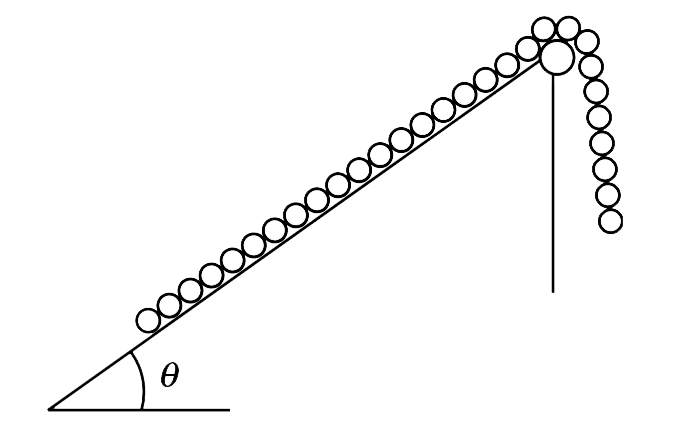
View SolutionA uniform chain of mass `m_0` and length l rests on a rough incline with its part hanging vertically as shown in the fig. The chain starts sliding up the incline (and hanging part moving down) provided the hanging part equals `eta` times the chain length (`eta` lt 1). What is the work performed by the friction force by the time chain slides completely off the incline. Neglect the dimension of pulley and assume it to be smooth.
View SolutionA large flat board is lying on a smooth ground. A disc of mass m = 2 kg is kept on the board. The coefficient of friction between the disc and the board is m = 0.2 . The disc and the board are moved with velocity `vec(u)=2hatims^(-1)` and `vec(V)=2hatJ ms^(-1)` respectively [in reference frame of the ground]. Calculate the power of the external force applied on the disc and the force applied on the board. At what rate heat is being dissipated due to friction between the board and the disc? [`g = 10 ms^(2)`]

View SolutionA car can pull a trailer of twice its mass up a certain slope at a maximum speed V. Without the trailer the maximum speed of the car, up the same slope is 2 V. The resistance to the motion is proportional to mass and square of speed. If the car (without trailer) starts to move down the same slope, with its engine shut off, prove that eventually it will acquire a constant speed. Find this speed.
View SolutionForce acting on a particle in a two dimensional XY space is given as `vec(F)=(3(Xhati+Yhatj))/((X^92)+Y^(2))^(3//2))`. Show that the force is conservative.
View SolutionIn a two dimensional space the potential energy function for a conservative force acting on a particle of mass m = 0.1 kg is given by U = 2 (x + y) joule (x and y are in m). The particle is being moved on a circular path at a constant speed of `V = 1 ms ^(-1)`. The equation of the circular path is `x^2 + y^2 = 42`. (a) Find the net external force (other than the conservative force) that must be acting on the particle when the particle is at (0, 4). (b) Calculate the work done by the external force in moving the particle from (4, 0) to (0, 4).
View SolutionA particle of mass m moves in xy plane such that its position vector, as a function of time, is given by `vec(r) =b(kt-sinkt)hati+b(kt+cos kt) hatj`. where b and k are positive constants. (a) Find the time `t_0` in the interval `o le t le (pi)/k` when the resultant force acting on the particle has zero power. (b) Find the work done by the resultant force acting on the particle in the interval `t_(o) le t le (pi)/4`
View SolutionA block of mass 2 kg is connect to an ideal spring and the system is placed on a smooth horizontal surface. The spring is pulled to move the block and at an instant the speed of end A of the spring and speed of the block were measured to be 6 m/s and 3 m/s respectively. At this moment the potential energy stored in the spring is increasing at a rate of 15 J/s. Find the acceleration of the block at this instant.

View SolutionA body of mass m was slowly hauled up the hill (figure) by a force F which at each point was directed along a tangent to the trajectory. Find the work performed by this force, if the height of the hill is h, the length of its base l, and the coefficient of friction k.

View SolutionIn previous problem what is the work done by `vec(F)` if the body started at rest at the base and has a velocity v on reaching the top?
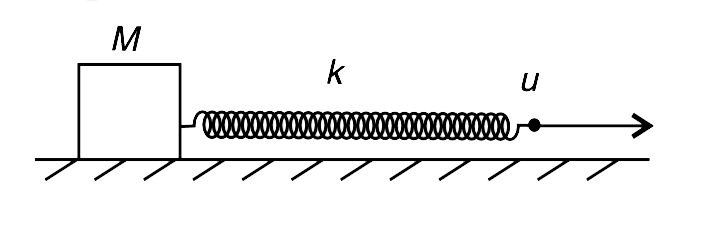
View SolutionA block of mass M is placed on a horizontal smooth table. It is attached to an ideal spring of force constant k as shown. The free end of the spring is pulled at a constant speed u. Find the maximum extension (`x_0`) in the spring during the subsequent motion.
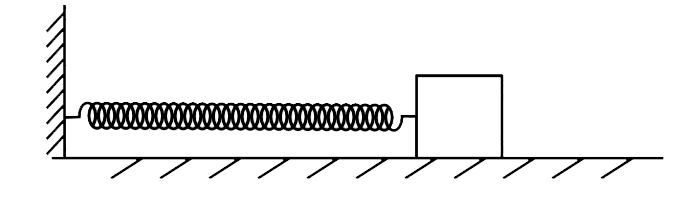
View SolutionA spring block system is placed on a rough horizontal floor. Force constant of the spring is k. The block is pulled to right to give the spring an elongation equal to `x_0` and then it is released. The block moves to left and stops at the position where the spring is relaxed. Calculate the maximum kinetic energy of the block during its motion.
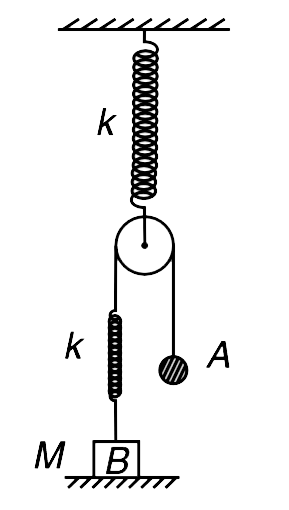
View SolutionIn the arrangement shown in the fig. string, springs and the pulley are mass less. Both the springs have a force constant of k and the mass of block B resting on the table is M. Ball A is released from rest when both the springs are in natural length and just taut. Find the minimum value of mass of A so that block B leaves contact with the table at some stage
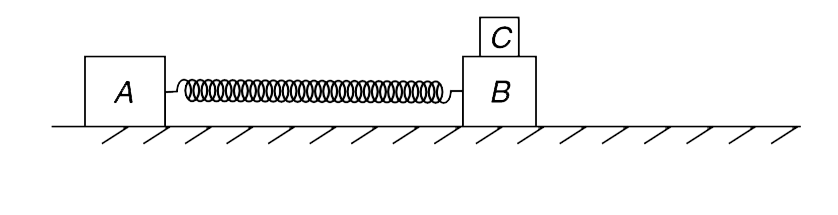
View SolutionTwo block A and B are connected to a spring (force constant k = 480 N/m) and placed on a horizontal surface. Another block C is placed on B. The coefficient of friction between the floor and block A is `mu_1 = 0.5`, whereas there is no friction between B and the floor. Coefficient of friction between C and B is `mu_2 = 0.85`. Masses of the blocks are `M_A = 50 kg, M_B = 28` kg and `M_C = 2 kg`. The system is held at rest with spring compressed by `x_0 = 0.5 m`. After the system is released, find the maximum speed of block B during subsequent motion.
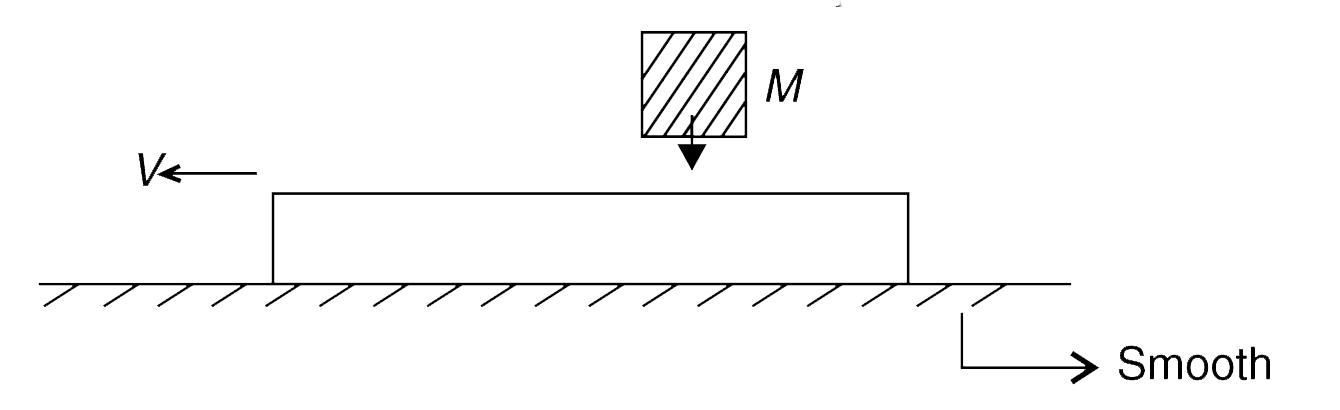
View SolutionA plank is moving along a smooth surface with a constant speed V. A block of mass M is gently placed on it. Initially the block slips and then acquires the constant speed (V) same as the plank. Throughout the period, a horizontal force is applied on the plank to keep its speed constant. (a) Find the work performed by the external force. (b) Find the heat developed due to friction between the block and the plank.
View SolutionA block of mass `m_1` is lying on the edge of a rough table. The coefficient of friction between the block and the table is `mu`. Another block of mass`m_2` is lying on another horizontal smooth table. The two block are connected by a horizontal spring of force constant K. Block of mass `m_2` is pulled to the right with a constant horizontal force F. (a) Find the maximum value of F for which the block of mass m1 does not fall off the edge. (b) Calculate the maximum speed that `m_2` can acquire under condition that `m_1` does not fall.

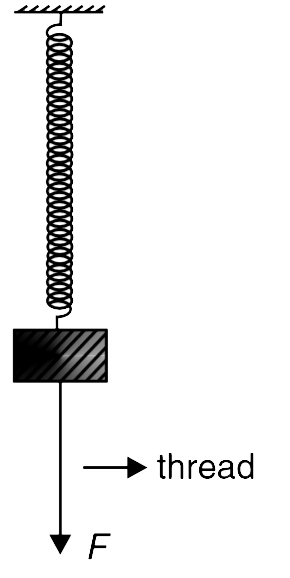
View SolutionA vertical spring supports a block in equilibrium. The spring is designed to break when extension in it crosses a limit. There is a light thread attached to the block as shown. The thread is pulled down with a force F which gradually increases from zero. The spring breaks when the force becomes `F_0`. Instead of gradually increasing the force, if the thread were pulled by applying a constant force, for what minimum value of the constant force the spring will break?
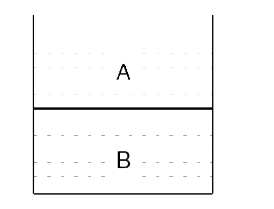
View SolutionTwo liquid A & B having densities `2rho` and `rho` respectively, are kept in a cylindrical container separated by a partition as shown in figure. The height of each liquid in the container is h and area of cross section of the container is A. Now the partition is removed. Calculate change in gravitational potential energy (`DeltaU`) of the system (a) assuming that the two liquids mix uniformly. (b) Assuming that the two liquids are immiscible. What do you conclude from the sign of `DeltaU` in the above two cases?
View SolutionA particle is projected at an angle `theta=30^(@)` with the horizontal. Two students A and B have drawn the variation of kinetic energy and gravitational potential energy of the particle as a function of time taking the point of projection as the reference level for the gravitational potential energy. Who is wrong and why?
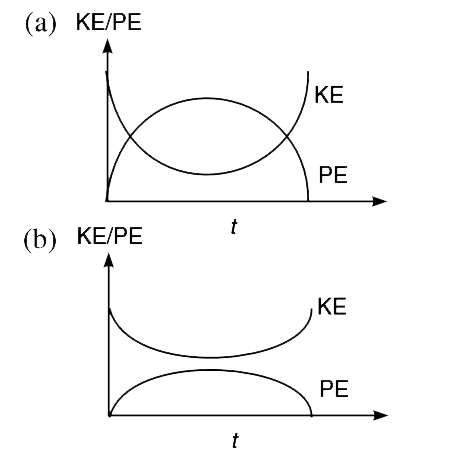
View SolutionTwo small rings each of mass ‘m’ are connected to a block of same mass ‘m’ through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings just taut. Length of each string is ‘l’. The system is released from the position shown. Find the speed of the block (v) and speed of the rings (u) when the strings make an angle of theta=60^(@)` with vertical. (Take `g = 10 m//s^2`)
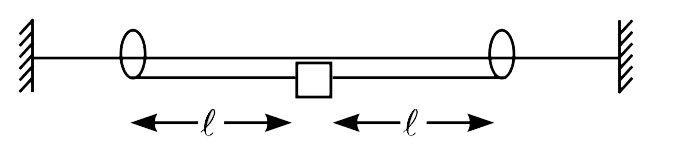
View SolutionA toy truck T at rest, has a hemispherical trough of radius R in it [O is the centre of the hemisphere]. A small block A is kept at the bottom of the trough. The truck is accelerated horizontally with an acceleration a. (i) Find the minimum value of a for which the block is able to move out of the trolley. (ii) If magnitude of a is twice the minimum value found in (i), find the maximum height (measured from its original level at the bottom of the trough) to which the block will rise.
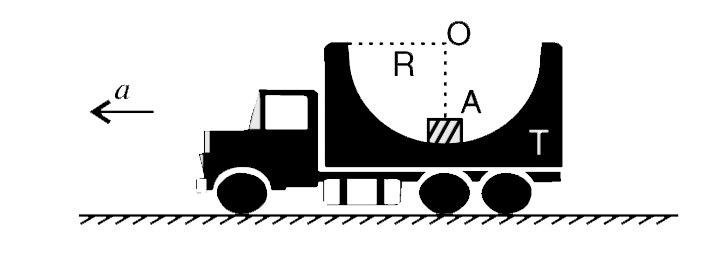
View SolutionA semicircular wire frame of radius R is standing vertical on a horizontal table. It is pulled horizontally towards right with a constant acceleration. A bead of mass m remain in equilibrium (relative to the semicircular wire) at a position where radius makes an angle q with horizontal. There is no friction between the wire and the bead. The bead is displaced a little bit in upward direction and released. Calculate the speed of the bead relative to the wire at the instant it strikes the table. Assume that all throughout the semicircular wire keeps moving with constant acceleration.
View SolutionA ideal spring of force constant k is connected to a small block of mass m using an inextensible light string (see fig). The pulley is mass less and friction coefficient between the block and the horizontal surface is `mu=1/(sqrt(3))`. The string between the pulley and the block is vertical and has length l. Find the minimum velocity u that must be given to the block in horizontal direction shown, so that subsequently it leaves contact with the horizontal surface. [Take `k=(2mg)/l`]

View SolutionA light spring is vertical and a mass less pan is attached to it. Force constant of the spring is k. A block of mass m is gently dropped on the pan. Plot the variation of spring potential energy, gravitation potential energy and the total potential energy of the system as a function of displacement (x) of the block. For gravitational potential energy take referece level to the initial postion of the pan.
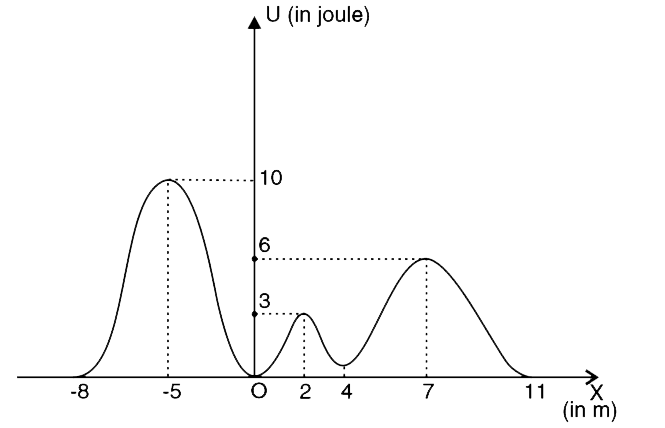
View SolutionA particle of mass m = 1.0 kg is free to move along the x axis. It is acted upon by a force which is described by the potential energy function represented in the graph below. The particle is projected towards left with a speed v, from the origin. Find minimum value of v for which the particle will escape far away from the origin.
View SolutionA particle of mass m = 1 kg is free to move along x axis under influence of a conservative force. The potential energy function for the particle is `U=a[(x/b)^(4)-5(x/b)^(2)]` joule
Where b = 1.0 m and a = 1.0 J. If the total mechanical energy of the particle is zero, find the co-ordinates where we can expect to find the particle and also calculate the maximum speed of the particle.
View SolutionA particle of mass m moves under the action of a central force. The potential energy function is given by `U(r)=mkr^(3)` Where k is a positive constant and r is distance of the particle from the centre of attraction. (a) What should be the kinetic energy of the particle so that it moves in a circle of radius a0 about the centre of attraction? (b) What is the period of this circualr motion ?
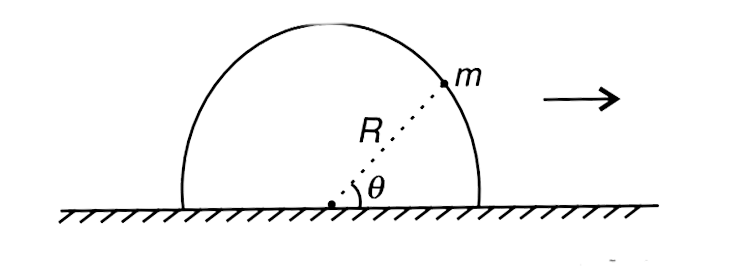
View SolutionA small block is placed on the top of a smooth inverted hemispherical bowl of radius R.

(a) The bowl is given a sudden impulse so that it begins moving horizontally with speed V. Find minimum value of V so that the block immediately loses contact with the bowl as it begins to move. (b) The bowl is given a constant acceleration ‘a’ in horizontal direction. Find maximum value of ‘a’ so that the block does not lose contact with the bowl by the time it rotates through an angle `theta=1^(@)` relative to the bowl. You can make suitable mathematical approximations justified for small value of angle `theta`.
View SolutionA pendulum bob is projected form its lowest position with velocity (u), in horizontal direction, that is just enough to make the string horizontal (position OC). At angular position q, at point B, the speed (V) of the bob was observed to be half its initial projection speed (u).
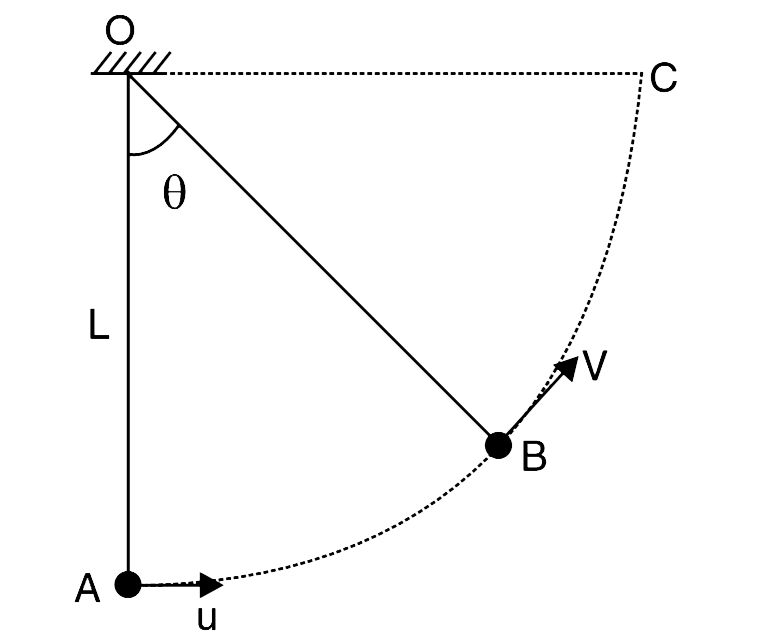
(a) Find `theta`
(b) Plot variation of magnitude of tangential acceleration of `theta`. (c) Let travel time from A to B be `t_(1)` and that from B to C be `t_(2)`. Looking at the graph obtained in part (b), tell which is larger `-t_(1)` or `t_(2)` ?
View SolutionA small ball is attached to an end of a light string of length R. It is suspended in vertical plane supported at point A. B and C are two nails (of negligible thickness) at a horizontal distance 0.3 R from A and a vertical distance 0.4 R above A respectively. The ball is given a horizontal velocity `u = sqrt5gR)` at its lowest point. Subsequently, after the string hitting the nails, the nails become the centre of rotation. Assume no loss in kinetic energy when the string hits the nails. It is known that the string will break if tension in it is suddenly increased by 200% or more.
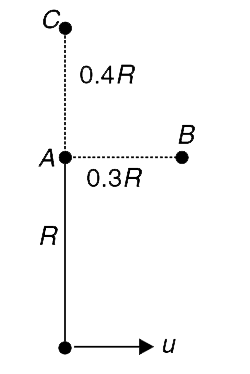
Will the string break during the motion? If yes, where? What is tension in the string at the instant the string breaks?
View SolutionA spherical balll of mass `m` is the highest point in the space between two fixed , concentic sphere `A` and `B` the smaller the two sphere `A` has a radius `R` and the space between the two spheres has a width `d` . The bell has a disneter very dightly less then d . All surface are frictionless . The bell is a given a gentle push (owards the right in the figure ) The upward vertical is denoted by `theta` (shown ijn the figure)

(a)Express the total normal reaction force exerted by the sphore on the as a finction of angle `theta`
(b) Let N_(A)` and N_(B)`denote in the magnitubes of the normal reaction force on the bell evered by the sphare `A` and `B` repectively Skech the variation of `N_(A) and`N_(B)` as functions of `cos theta ` in the range `0 le theta le pi ` by drawing two separate graph in your answer book taking `cos theta ` an the horizental axas.
View SolutionA particle is suspended vertically from a point O by an inextensible mass less string of length L. A vertical line AB is at a distance of `L/8` from O as shown in figure. The particle is given a horizontal velocity u. At some point, its motion ceases to be circular and eventually the object passes through the line AB. At the instant of crossing AB, its velocity is horizontal. Find u.

View SolutionA simple pendulum has a bob of mass m and string of length R. The bob is projected from lowest position giving it a horizontal velocity just enough for it to complete the vertical circle. Let the angular displacement of the pendulum from its initial vertical position be represented by `theta`. Plot the variation of kinetic energy (kE) of the bob and the tension (T) in the string with `theta`. Plot the graph for one complete rotation of the pendulum.
View SolutionA light thread is tightly wrapped around a fixed disc of radius R. A particle of mass m is tied to the end P of the thread and the vertically hanging part of the string has length `piR`. The particle is imparted a horizontal velocity `V=sqrt((4pigR)/3)`. The string wraps around the disc as the particle moves up. At the instant the velocity of the particle makes an angle of `theta=60^(@)` with horizontal, calculate.
(a) Speed of the particle
(b) Tension in the string
View SolutionAn experimenter is inside a train. He observes that minimum speed at lowest position needed by a pendulum bob to complete a vertical circle is 10 m/s. Calculate the minimum speed (u) needed at the lowest position so as to complete the vertical circle when the train is moving horizontally at an acceleration of `a = 7.5 m//s^2`. Find the maximum tension in the string during the motion. [`g = 10 m//s^2`].
View SolutionA small body of mass m lies on a horizontal plane. The body is given a velocity `v_0`, along the plane. (a) Find the mean power developed by the friction during the whole time of motion, if friction coefficient is `mu = 0.3, m = 2.0 kg` and `v_0` = 3 m/s. (b) Find the maximum instantaneous power developed by the friction force, if the friction coefficient varies as `mu =alphax`, where `alpha` is a constant and x is distance from the starting point
View SolutionTwo particles of masses M and m (M gt m) are connected by a light string of length `piR`. The string is hung over a fixed circular frame of radius R.

Initially the particles lie at the ends of the horizontal diameter of the circle (see figure). Neglect friction. (a) If the system is released, and if m remains in contact with the circle, find the speed of the masses when M has descended through a distance `R theta (theta lt pi)`. (b) Find the reaction force between the frame and m at this instant. (c) Prove that m1 will certainly remain in contact with the frame, just after the release, if 3m gt M.
View SolutionA small object is sliding on a smooth horizontal floor along a vertical wall. The wall makes a smooth turn by an angle `theta_(0)` . Coefficient of friction between the wall and the block is `mu`. Speed of the object before the turn is u. Find its speed (V) just after completing the turn. Does your answer depend on shape of the curve? [The turn is smooth and there are no sharp corners.]

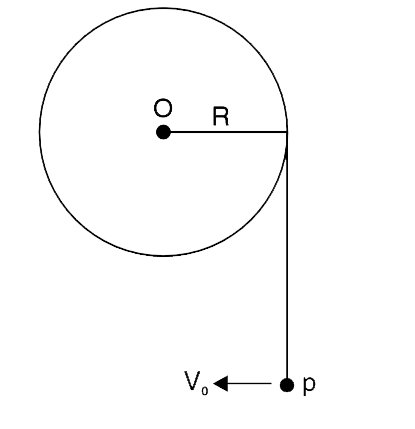
View SolutionAB is a vertically suspended elastic cord of negligible mass and length L. Its force constant is `k=(4mg)/L`. There is a massless platform attached to the lower end of the cord. A monkey of mass m starts from top end A and slides down the cord with a uniform acceleration of `g/2` . Just before landing on the platform, the monkey loses grip on the cord. After landing on the platform the monkey stays on it. Calculate the maximum extension in the elastic cord.
View SolutionThe pulleys and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle `theta` should be

View SolutionThree identical masses are attached to the ends of light strings, the other ends of which are connected together as shown in the figure. Each of the three strings has a length of 3 m. The three masses are dropped through three holes in a table and the system is allowed to reach equilibrium.
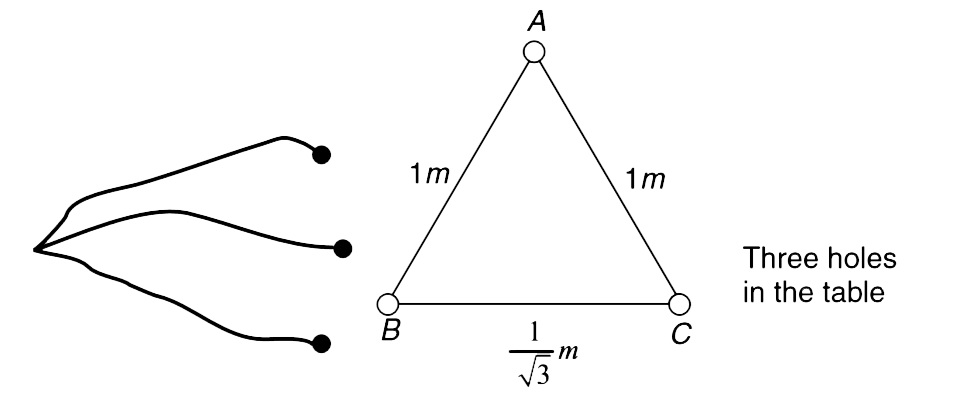
(a) What is total length of the strings lying on the table in equilibrium? (b) Select a point K inside the `triangleABC` such that AK + BK + CK is minimum, use the result obtained in (a) and the fact that potential energy of the system will be minimum when it is in equilibrium.
View Solution
All Questions questions and complete solutions for chapter WORK, POWER AND ENERGY of ARIHANT PHYSICS (HINGLISH) of Class 11