Complete Solutions to Momentum And Center of Mass of chapter MOMENTUM AND CENTRE OF MASS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOMENTUM AND CENTRE OF MASS |
| ARIHANT MASTER PROBLEM | Momentum And Center of Mass |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A particle is acted upon by a force for 1 second whose X component remains constant at `F_(x) = 30 N` but y and z components vary with time as shown in the graph. Calculate the magnitude of change in momentum of the particle in 1 s. What angle does the change in momentum `(Delta vec(P))` make with X axis ?

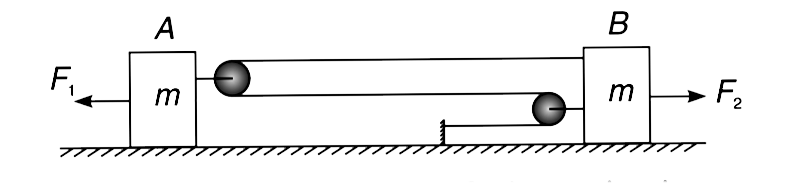
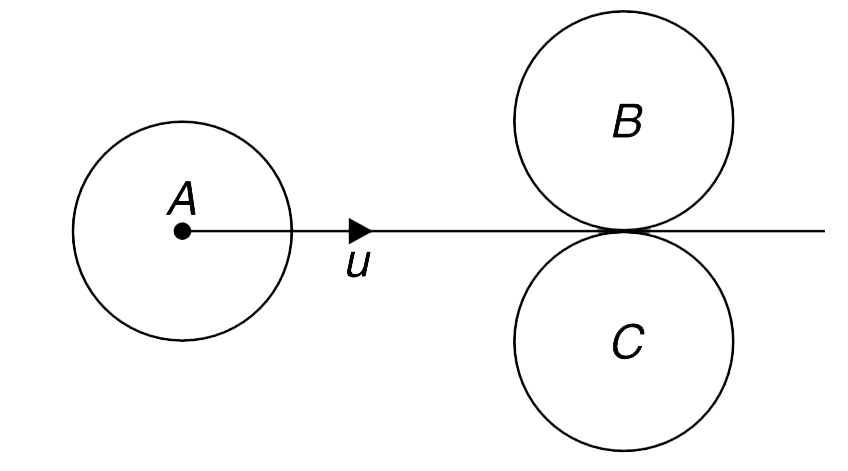
View SolutionTwo block A and B of equal mass are connected using a light inextensible string passing over two light smooth pulleys fixed to the blocks (see fig). The horizontal surface is smooth. Every segment of the string (that is not touching the pulley) is horizontal. When a horizontal force `F_(1)` is applied to A the magnitude of momentum of the system, comprising of A + B, changes at a rate R. When a horizontal force `F_(2)` is applied to B (`F_(1)` not applied) the magnitude of momentum of the system A + B once again changes at the rate R. Which force is larger `- F_(1) or F_(2)` ?
View SolutionA particle of mass `m = 1 kg` is moving in space in X direction with a velocity of `10 ms^(-1)`. A 4 N force acting in Y direction is applied on it for a time interval of `5.0 s`. Later a 5 N force was applied on it in Z direction for `4.0 s`
(a) Calculate the total work done by both the forces.
(b) Which force performed greater work ?
View SolutionAn observer `O_(1)` standing on ground finds that momentum of a projectile of mass `2 kg` changes with time as `vec(P)_(01) =(4that (i) + 20 t hat(k))kg m//s` Acceleration due to gravity is `vec(g)=(10 hat(k))m//s^(2)` and there is a wind blowing in horizontal direction. Another observer `O_(2)` driving a car observes that momentum of the same projectile changes with time as -
`vec(P)_(02)=(8t hat(i)-16 hat(t) hat(j)+20 t hat(k))kg m//s`. Find the acceleration of the car at `t = (1)/(8) s`
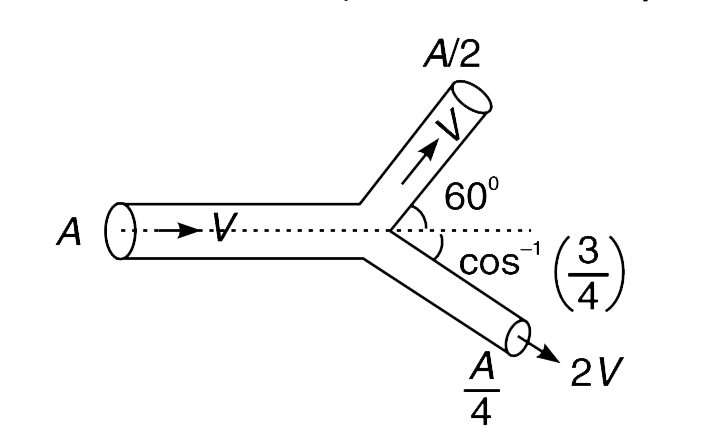
View SolutionWater flows through a tube assembly as shown in the fig. Speed of flow (marked as `V and 2V`), cross sectional area (A, A/2 and A/4) and the angles between segments has been shown in fig. Calculate the force applied by the water flow on the tube. Take density of water to be `rho`.
View SolutionA man is running along a road with speed u. On his chest there is a paper of mass m and area S. There is a wind blowing against the man at speed V. Density of air is `rho`. Assume that the air molecules after striking the paper come to rest relative to the man. Find the minimum coefficient of friction between the paper and the chest so that the paper does not fall ?
View SolutionTwo particles A and B of mass 2 m and m respectively attract each other by mutual gravitational force and no other force acts on them. At time t = 0, A was observed to be at rest and B was moving away from A with a speed u. At a later time t it was observed that B was moving towards A with speed u. Assume no collision has taken place by then. Find work done by the gravitational force in the time interval 0 to t
View Solution(i) A block of mass m moving towards right with a velocity V strikes (head on) another block of mass M which is at rest connected to a spring. The coefficient of restitution for collision between the blocks is e = 0.5.
Find the ratio `(M)/(m)` for which the subsequent compression in the spring is maximum. There is not friction.

Ball A collides head on with another identical ball B at rest. Find the coefficient of restitution if ball B has 80% of the total kinetic energy of the system after collision.
View SolutionA ball having mass m and velocity u makes a head on collision with another ball. After collision velocity of the ball of mass m was found to be V in the direction of its original motion. The interaction force between the two balls during their collision has been shown in the graph. The area of the shaded part of the graph is same as the area of the not shaded part. Find the velocity of the balls at the instant they were having equal velocity.
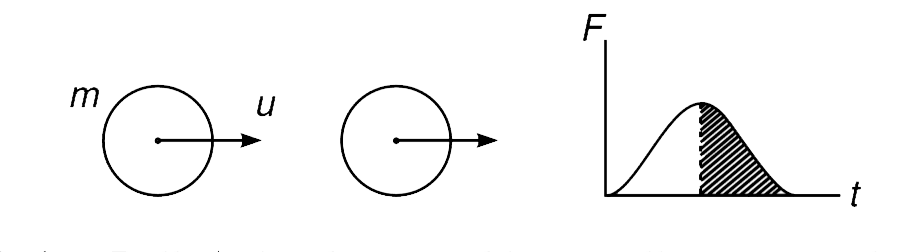
View SolutionBall A is about to hit a wall at an angle of incidence of `theta = 30^(@)`. But before hitting the wall it made a head on collision with another identical ball B. The ball B then collides with the wall. The coefficient of restitution for collision between two balls is `e_(1) = 0.8` and that between a ball and the wall is `e_(1) = 0.6`. Find the final velocity of ball B. Initial velocity of A was `u = 5 ms^(-1)`. Neglect friction.
`[tan^(-1)((2.25)/(2.34))=44^(@)]`

View SolutionTwo identical balls A and B are moving as shown in the fig. Ball A hits a smooth floor head on with a velocity u and at the same instant ball B strikes A head on with a horizontal velocity u. The collision between A and B is perfectly inelastic whereas the coefficient of restitution for collision between A and the floor is `e = 0.5`. At what time the two balls will collide again? Assume friction to be absent everywhere.

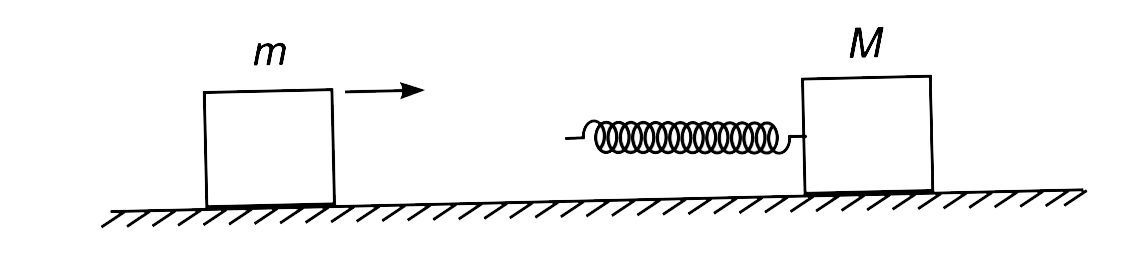
View SolutionTwo blocks of mass m and M are lying on a smooth table. A spring is attached with the block of mass M (see fig). Block of mass m is given a velocity towards the other block. Find the value of `(M)/(m)` for which the kinetic energy of the system will never fall below one third of the initial kinetic energy imparted to the block of mass m.
View SolutionTwo identical blocks A and B have two identical springs fixed to them (see fig). Mass of each block is M and force constant of each spring is K. The two blocks have been placed on a smooth table. Another block C of mass m `(lt lt M)` is placed between A and B and is held close to A so as to compress the spring attached to A by `X_(0)`. From this position the system is released. C moves to push B and then is back to push A. The sequence continues until all interactions between the blocks cease. Find the speeds eventually acquired by A and B.

View SolutionA particle of mass m is flying horizontally at velocity u. It strikes a smooth inclined surface and its velocity becomes vertical.
(a) Find the loss in kinetic energy of the particle due to impact if the inclination of the incline is `60^(@)` to the horizontal.
(b) Can the particle go vertically up after collision if inclination of the incline is `30^(@)` ?

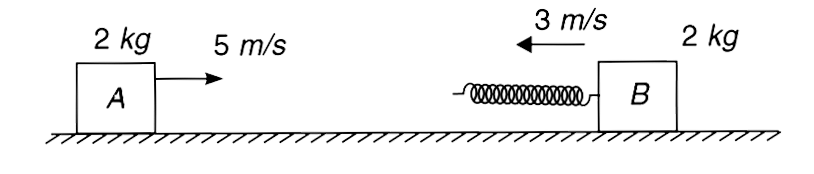
View SolutionA block A of mass `2 kg` is moving to right with a speed of 5 m/s on a horizontal smooth surface. Another block B of mass 2 kg, with a mass less spring of force constant `K =200` N/m attached to it, is moving to left on the same surface with a speed of 3 m/s. Block A collides with the spring attached to B. Calculate
(a) the final velocity of the block A.
(b) the minimum kinetic energy of the system of two blocks during subsequent motion.
(c) Repeat part (b) if there is no spring and the two blocks collide head on. Assume that the blocks are made of perfectly elastic material
View SolutionA box of mass M is at rest on a horizontal surface. A boy of mass `m (lt M)` wants to push the box by applying a horizontal force on it. The boy knows that he will not be able to push the box as the coefficient of friction `mu` between his shoes and ground is almost equal to that between the box and the ground. He decides to run, acquire a speed u and then bang into the box. After hitting the box, the boy keeps pushing as hard as possible. What is the maximum distance through which the box can be displaced this way ?

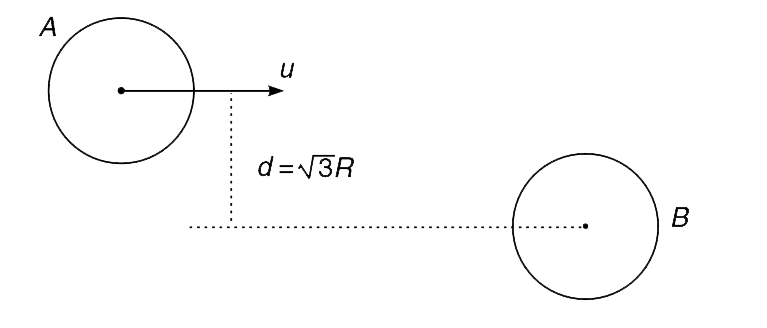
View SolutionA smooth ball A travels towards another identical ball B with a velocity u. Ball B is at rest and the impact parameter d is equal to `sqrt(3) R` where `R` is radius of each ball. Due to impact the direction of motion of ball A changes by `30^(@)`. Find the velocity of B after the impact. It is given that collision is elastic
View Solution(a) Two identical balls are moving along X axis and undergo an elastic collision. Plot the position time graph for the two balls.
(b) Consider five identical balls moving along X axis. What is the maximum number of collisions that is possible? Assume that more than two balls do not collide at the same time and collisions are elastic.
View SolutionTwo particles of mass m each are attached to the end of a mass less spring. This dumb-bell is moving towards right on a smooth horizontal surface at speed V with the spring relaxed. Another identical dumb-bell is moving along the same line is opposite direction with the same speed. The two dumb-bells collide head on and collision is elastic. Assuming collisions to be instantaneous, how many collisions will take place ?

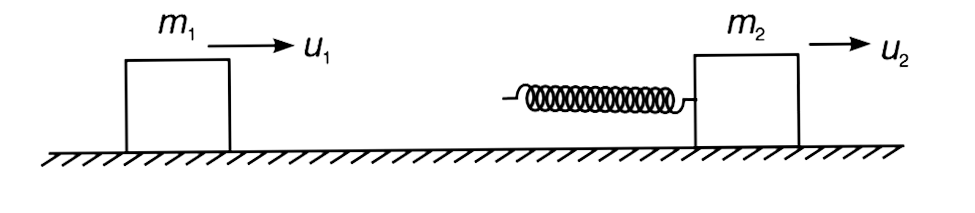
View SolutionTwo blocks of mass `m_(1) and m_(2)` are moving along a smooth horizontal floor. A non-ideal spring is attached at the back of mass `m_(2)`. Initial velocities of the blocks are `u_(1) and u_(2)` as shown, with `u_(1) gt u_(2)`. After collision the two blocks were found to be moving with velocities `V_(1) and V_(2)` respectively. Find the ratio of impulse (on each block) during the deformation phase of the spring and that during its restoration phase. [By non ideal spring we mean that it does not completely regain its original shape after deformation. You can neglect the mass of the spring.]
View SolutionA ball moving with velocity `V_(0)`, makes a head on collision with another identical ball at rest. The velocity of incident ball and the other ball after collision is `V_(1)` and `V_(2)` respectively.
(a) Using momentum conservation write an equation having `V_(1) and V_(2)` as unknowns. Plot a graph of `V_(1)` vs `V_(2)` using this equation.
(b) Assuming the collision to be elastic write an equation for kinetic energy. Plot a graph of `V_(1)` vs `V_(2)` using this equation.
(c) The intersection point of the above two graphs gives solution. Find `V_(1) and V_(2)` .
(d) In a particular collision, the plot of graphs mentioned above is as shown in figure

Find `V_(1) and V_(2)` for this collision. Also write the percentage loss in kinetic energy during the collision.
View SolutionA particle having charge `+q` and mass m is approaching (head on) a free particle having mass M and charge 10 q. Initially the mass m is at large distance and has a velocity `V_(0)`, whereas the other particle is at rest.
(a) Find the final velocity of the two particles when `M = 20` m.
(b) Find the final state of the two particles if `M = m`.

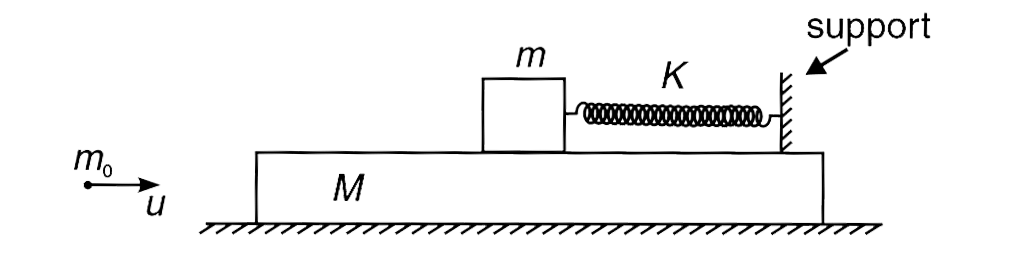
View SolutionIn the system shown in fig. block of mass M is placed on a smooth horizontal surface. There is a mass less rigid support attached to the block. Block of mass m is placed on the first block and it is connected to the support with a spring of force constant K. There is no friction between the blocks. A bullet of mass `m_(0)`, moving with speed `u` hits the block of mass M and gets embedded into it. The collision is instantaneous. Assuming that m always stays over M, calculate the maximum extension in the spring caused during the subsequent motion.
`K=8960 N//m , u=400 m//s`
View SolutionStarting from a height H, a ball slips without friction, down a plane inclined at an angle of `30^(@)` to the horizontal (fig.). After leaving the inclined plane it fall under gravity on a parabolic path and hits the horizontal ground surface. The impact is perfectly elastic (It means that there is no change in horizontal component of ball’s velocity and its vertical velocity component gets inverted. There is no change in speed due to collision). Will the ball rise to a height equal to H or less than H after the impact ?
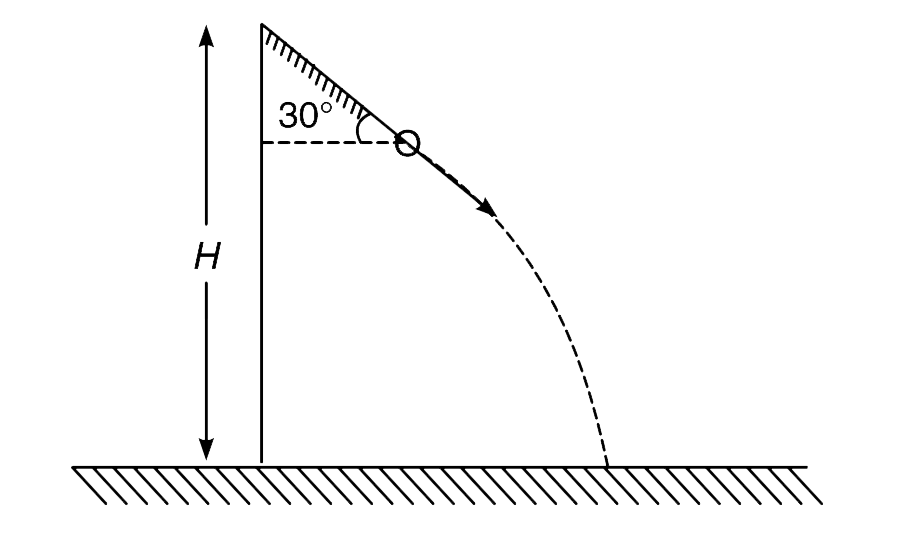
View SolutionHailstorms are observed to strike the surface of a frozen lake at an angle of `30^(@)` with the vertical and rebound at an angle of `60^(@)` with vertical. Assuming the contact to be smooth, the coefficient of restitution is
View SolutionA ball of mass m approaches a heavy wall of mass M with speed 4 m/s along the normal to the wall. The speed of wall before collision is 1m/s towards the ball. The ball collides elastically with the wall. What can you say about the speed of the ball after collision? Will it be slightly less than or slightly higher than 6 m/s ?
View SolutionA particle is thrown upward with speed `20 sqrt(2)` m/s. It strikes the inclined surface as shown in the figure. Collision of particle and inclined surface is perfectly inelastic. What will be maximum height (in m) attained by the particle from the ground `(g = 10 m/s^(2))`

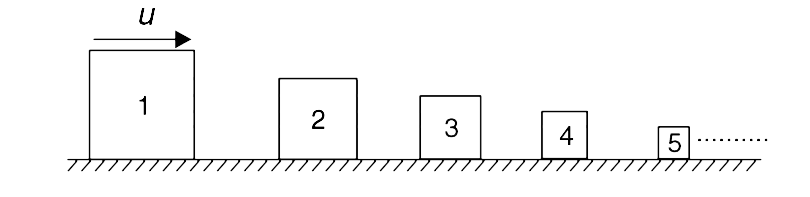
View Solution2n identical cubical blocks are kept in a straight line on a horizontal smooth surface. The separation between any two consecutive blocks is same. The odd numbered blocks `1, 3, 5,.....(2n–1)` are given velocity `v` to the right whereas blocks `2, 4, 6,......2n` are given velocity `v` to the left. All collisions between blocks are perfectly elastic. Calculate the total number of collisions that will take place.

View SolutionA small ball with mass `M = 0.2 kg` rests on top of a vertical column with height `h = 5 m`. A bullet with mass m `= 0.01 kg`, moving with velocity `v_(0) = 500 m//s`, passes horizontally through the center of the ball. The ball reaches the ground at a horizontal distance `s = 20 m` from the column. Where does the bullet reach the ground? What part of the kinetic energy of the bullet was converted into heat when the bullet passed through the ball? Neglect resistance of the air. Assume that `g = 10 m//s^(2)`.
View SolutionFigure shows a circular frictionless track of radius R, centred at point O. A particle of mass M is released from point `A (OA = R//2)`. After collision with the track, the particle moves along the track.
(a) Find the coefficient of restitution `e`.
(b) What will be value of `e` if the velocity of the particle becomes horizontal just after collision ?
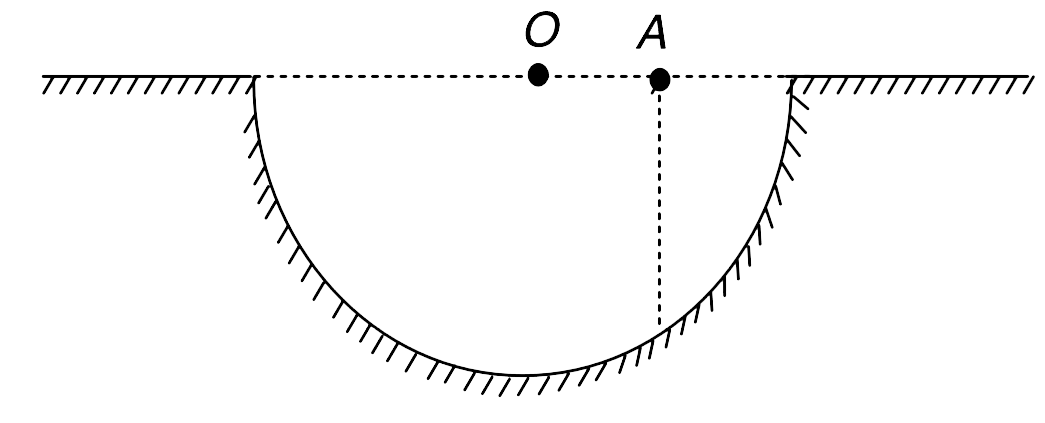
View SolutionA rectangular billiard table has dimensions `AB = 4 sqrt(3)` feet and `BC = 2` feet. Ball 1 is at the centre of the table. Ball 2 moving perpendicular to CD hits ball 1. After the collision ball 2 itself goes straight into the hole at. A Prove that ball 1 will fall into the hole at C. Assume that the balls are identical and their dimensions are too small compared to the dimensions of a hole. All collisions are elastic
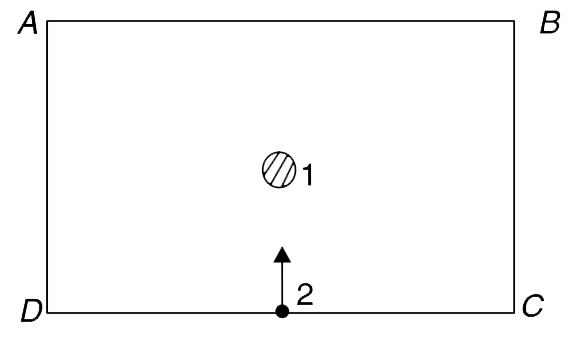
View SolutionBlocks shown in figure have been placed on a smooth horizontal surface and mass of `(n + 1)^(th)` block is `(1)/(20)` times the mass of `n^(th)` block (where `n=1,2,3,4,….`). The first block is given an initial velocity `u` towards the second block. All collision are head on elastic collisions. If `u = 10 m//s` then how many blocks must be kept so that the last one acquires speed equal to or greater than the escape speed `(=11.0 km s^(-1))`
[Take `log_(10)((40)/(21))=0.28 and log_(10)(11)=1.04`]
View SolutionThere is a long narrow and smooth groove in a horizontal table. Two identical blocks A and B each of mass m are placed inside the groove at some separation. An ideal spring is fixed to A as shown. Block A is given a velocity `u` to the right and it interacts with B through the spring.

(a) What will be final state of motion of the two blocks ?
(b) During their course of interaction what is the minimum kinetic energy of the system ?
(c) The spring is removed and the two blocks are tied using a mass less string. Now A is set into motion with speed `u`. What will be the final state of motion of the two blocks in this case ? How much kinetic energy is lost by the system ? Where goes this energy ?

View SolutionA carpet lying on ground has length `L`, width a and a small thickness `d`. It is rolled over a light cylindrical pipe of radius `r = (L)/(100 sqrt(pi))` and kept on a level ground. Increase in gravitational potential energy of the carpet is `DeltaU_(1)` (compared to its initial position when it was lying flat). In another experiment the carpet was folded to give it a shape of a cuboid (see figure) having width `b`. When this is placed on level ground its gravitational potential energy is `Delta U_(2)` higher than its initial position (flat on ground). It is given that `d = 10^(-4) L`. Find `b` for which `DeltaU_(1) = Delta U_(2)`. [Take `sqrt((pi)/(2)) = 1.25`]
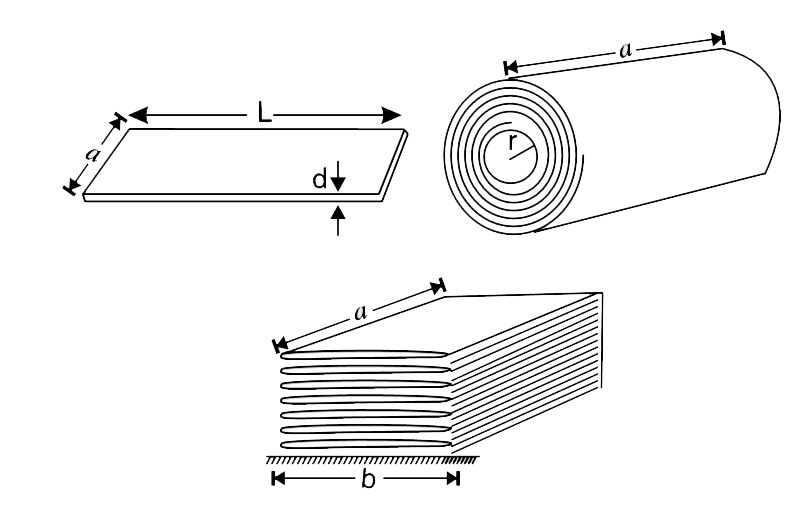
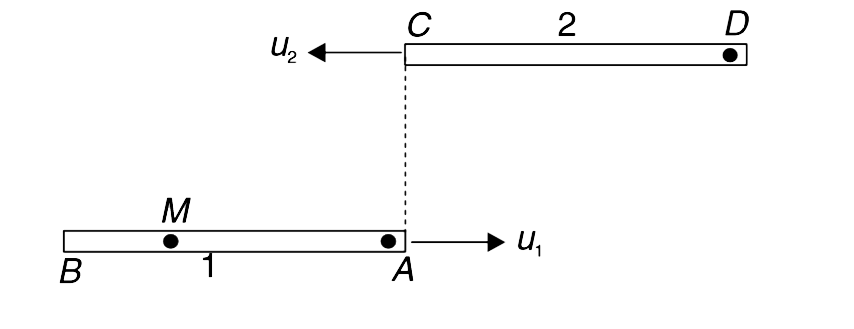
View SolutionTwo identical thin rods are welded as shown in the fig. B is midpoint of rod CD. Now the system is cut into two parts through its center of mass M. The part AM weights 4 kg. Find the mass of the other part.
View Solution(i) A regular polygon has 2016 sides and r is the radius of the circle circumscribing the polygon. Particles of equal mass are placed at 2015 vertices of the polygon. Find the distance of the centre of mass of the particle system from the centre of the polygon.
(ii) In the last problem you have been asked to remove any one particle from the system so that the centre of mass of the remaining 2014 particles lies farthest from the geometrical centre of the polygon. Which particle will you remove ?
View SolutionTwo identical block A and B each having mass m, are connected with a spring of force constant k. The floor is smooth and A is pushed so as to compress the spring by `x_(0)`. The system is released from this position
(a) Calculate the maximum speed of the centre of mass of the system during subsequent motion.
(b) What is acceleration of the centre of mass at the instant it acquires half its maximum speed ?
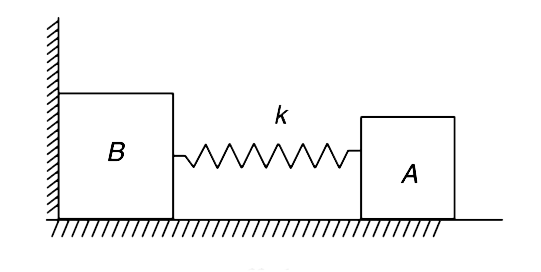
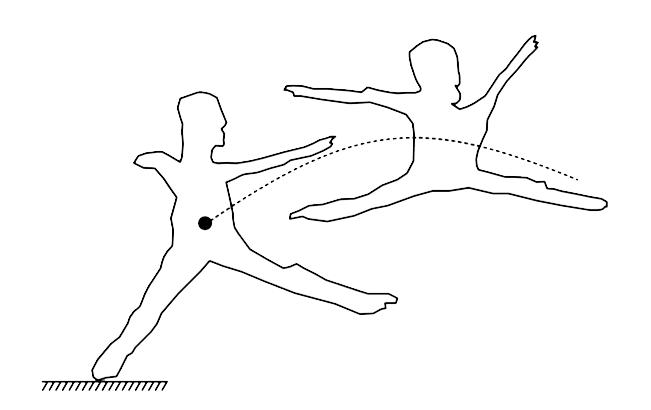
View SolutionA dancer leaps off the floor with her centre of mass having a velocity of 5 m/s making an angle of `theta =37^(@)` to the horizontal. At the top of the trajectory the dancer has her legs stretched so that the centre of mass gets closer to head by a vertical distance of `0.25 m`. By how much does the head rises vertically from its initial position ? `[ sin 37^(@) = (3)/(5)]`
View SolutionIn order to make a jump straight up, a `60 kg` player starts the motion crouched down at rest. He pushes hard against the ground, raising his centre of mass by a height `h_(0) = 0.5 m`. Assume that his legs exert a constant force `F_(0)` during this motion. At this point, where his centre of mass has gone up by `h_(0)` his feet leave the ground and he has an upward velocity of `v`. Centre of mass of his body rises further by `h = 0.8 m` before falling down [Take `g = 10 m//s^(2)`]
(a) Find `v`.
(b) Find the normal force applied by the ground on his feet just before he left the ground.
View SolutionA platform is kept on a rough horizontal surface. At one end A of the platform there is a man standing on it. The man runs towards the end B and the platform is found to be moving. In which direction will the platform be moving after the man abruptly comes to rest on the platform at B ?
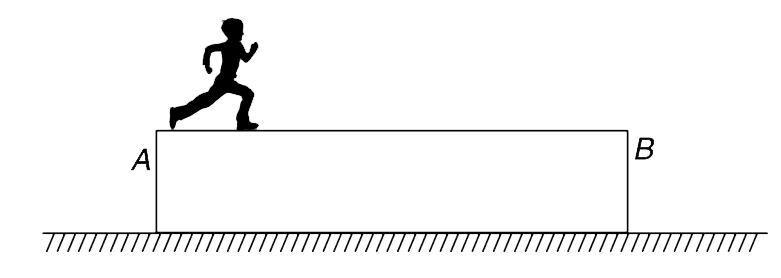
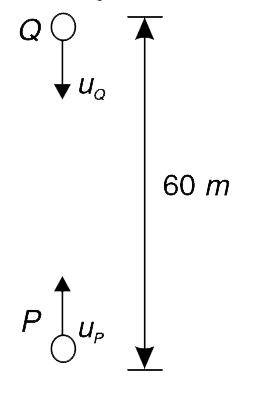
View SolutionTwo particles `P and Q` have mass `1 kg and 2 kg` respectively. They are projected along a vertical line with velocity `u_(p) = 20` m/s and `u_(Q) = 5` m/s when separation between them was 60 m. P was projected vertically up while Q was projected vertically down. Calculate the maximum height attained by the centre of mass of the system of two particles, measured from the initial position of P. Assume that the particles do not collide and that the ground is far below their point of projection `[g = 10 m//s^(2)] `
View SolutionTwo small motors are kept on a smooth table at a separation `L`. The motors have mass `M and 2M` and are connected by a light thread. The motors begin to wrap the thread and thereby move closer to each other. The tension in the thread is maintained constant at F. Find the time after which the two motors will collide. Neglect the dimensions of the motors and their stands.

View SolutionConsider a uniform rectangular plate. If a straight line is drawn, passing through its centre of mass (in the plane of the plate), so as to cut the plate in two parts – the two parts obtained are of equal mass irrespective of the orientation of the line. Can you also say that a straight line passing through the centre of mass of a triangular plate, irrespective of its orientation, will also divide the triangle into two pieces of equal mass ?
View SolutionTwo spherical bodies of masses m and 5m and radii R and 2R respectively, are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, the distance covered by smaller sphere just before collision is
View SolutionA shell is fired vertically upward with a speed of 60 m/s. When at its maximum height it explodes into large number of fragments. Assume that the fragments fly in every possible direction and all of them have same initial speed of 25 m/s [Take `g = 10 m//s^(2)`]
(a) Prove that after the explosion all the fragments will lie on an expanding sphere. What will be speed of the centre of the sphere thus formed – one second after explosion ?
(b) Find the radius of the above mentioned sphere at the instant the bottom of the sphere touches the ground.
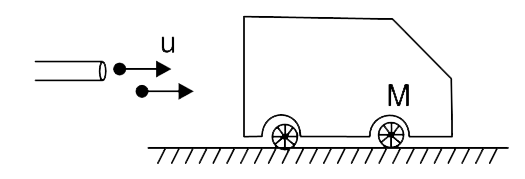
View SolutionA car of mass M is free to move on a frictionless horizontal surface. A gun fires bullets on the car. The bullets leave the stationary gun with speed `u` and mass rate `b kg s^(-1)`. The bullets hit the vertical rear surface of the car while travelling horizontally and collisions are elastic. If the car starts at rest find its speed and position as a function of time. Mass of the car `M gt gt` mass of each bullet.
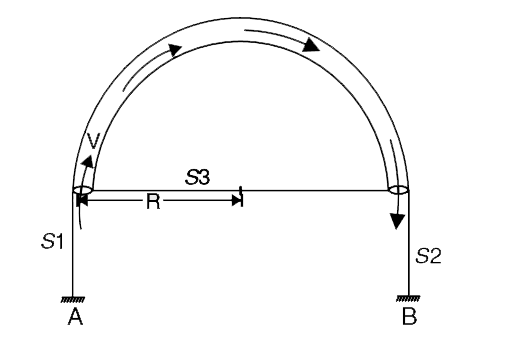
View Solution(i) Liquid of density `rho` flows at speed `upsilon` along a flexible pipe bent into a semicircle of radius R. The cross sectional area of the pipe is A and its cross sectional radius is small compared to R. Three strings `S_(1), S_(2) and S_(3)` keep the pipe in place. `S_(3)` ties the two ends of the pipe and the other two string have their ends secured at A and B. Strings `S_(1) and S_(2)` are perpendicular to the string `S_(3)`. The entire system is in horizontal plane. Find the tension in the three strings
(ii) A car of mass `M` is moving with a velocity `V_(0)` on a smooth horizontal surface. Bullets, each of mass m, are fired horizontally perpendicular to the velocity of the car with a speed `u` relative to the car. After firing n bullets it was found that the car was travelling with velocity `V_(0)` in a direction opposite to its original direction of motion. Assume that mu `lt lt MV_(0)` and also that nm `lt lt M`. Find n in terms of other given parameters.
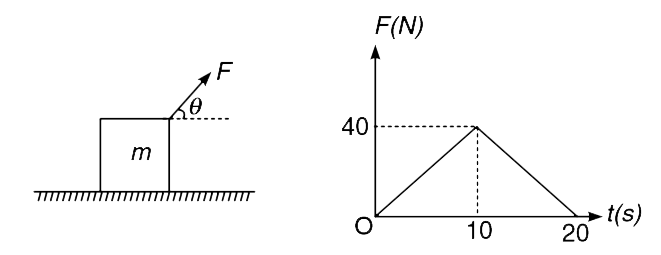
View SolutionA block of mass `m = 4.4 kg` lies on a horizontal rough surface. The coefficient of friction between the block and the surface is `mu = 0.5`. A force `F` starts acting on the block making an angle `theta = 37^(@)` to the horizontal. The force changes with time as shown in the graph.
(a) At what time the block begins to move ?
(b) Calculate the maximum speed attained by the block.
`[tan 37^(@)=(3)/(4) ,g = 10 ms^(-2)]`
View SolutionA heavy block A is made to move uniformly along a smooth floor with velocity `V = 0.01` m/s towards left. A ball of mass `m = 50 g` is projected towards the block with a velocity of `u = 100` m/s. The ball keeps bouncing back and forth between the block A and fixed wall B. Each of the collisions is elastic. After the ball has made 1000 collisions with the block and wall each, the distance between the block and the wall was found to be `L = 1.2 m`. Calculate the average force being experienced by the block due to collision at this instant. All collision are instantaneous
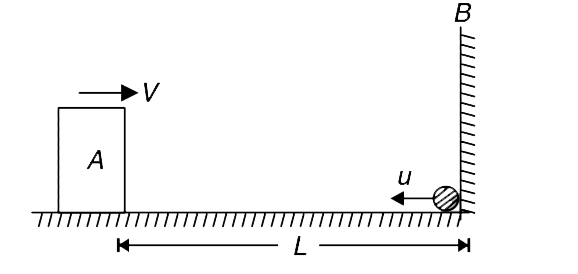
View SolutionA chain (A) of length L is coiled up on the edge of a table. Another identical chain (B) is placed straight on the table as shown. A very small length of both the chains is pushed off the edge and it starts falling under gravity. There is no friction

(a) Find the acceleration of the chain B at the instant `L_(2)` length of it is hanging. Assume no kinks in the chain so that the entire chain moves with same speed.
(b) For chain A assume that velocity of each element remains zero until it is jerked into motion with a velocity equal to that of the falling section. Find acceleration of the hanging section at the instant a length `l_(0)` has slipped off the table and its speed is known to be `v_(0)` at the instant.
View SolutionTo understand the effect of air resistance on the motion of a bullet let's consider a bullet of the shape shown in the fig. The bullet is flying horizontally. The cross section of cylindrical part is A and the conical part has a semi vertical angle of `45^(@)`. Assume that the bullet is fired with initial velocity `u` and moves in a gaseous medium in which molecules are at rest (do you think this assumption is necessary?). Collisions of the molecules with the bullet are elastic. Take mass of bullet to be M, density of gaseous medium as `rho` and disregard gravity.
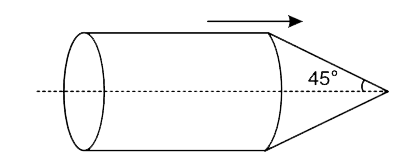
(a) Consider two bullets one small and other large, made of same material. Which will experience larger retardation due to air resistance ?
(b) Write the speed of bullet after time t
(c) Write distance travelled by the bullet in time t.
View SolutionTwo particle A and B, of mass `3m and 2m` respectively, are attached to the ends of a light inextensible string which passes over a smooth fixed pulley of negligible mass. After the system is released and A falls through a distance L, it hits a horizontal inelastic table so that its speed is immediately reduced to zero. Assume that B never hits the table or the pulley. Find
(a) the time for which A is resting on the table after the first collision and before it is jerked off,
(b) the difference between the total kinetic energy of the system immediately before A first hits the table and total kinetic energy immediately after A starts moving upwards for the first time. Explain the loss in kinetic energy.

View SolutionA light rod of length `L` is hinged to a plank of mass m. The plank is lying on the edge of a horizontal table such that the rod can swing freely in the vertical plane without any hindrance from the table. A particle of mass `m` is attached to the end of the rod and system is released from `theta = 0^(@)` position (see figure)

(a) Assume that friction between the plank and the table is large enough to prevent it from slipping and calculate the smallest normal force applied by the plank on the table.
(b) Assume that friction is absent everywhere and calculate the speed of the plank when the rod makes `theta = 180^(@)`.
View SolutionA block of mass `M = 5 kg` is moving on a horizontal table and the coefficient of friction is `mu = 0.4`. A clay ball of mass `m = 1 kg` is dropped on the block, hitting it with a vertical velocity of `u = 10` m/s. At the instant of hit, the block was having a horizontal velocity of `v = 2` m/s. After an interval of t, another similar clay ball hits the block and the system comes to rest immediately after the hit. Assume that the clay balls stick to the block and collision is momentary. Find t. Take `g = 10 m//s^(2)`.

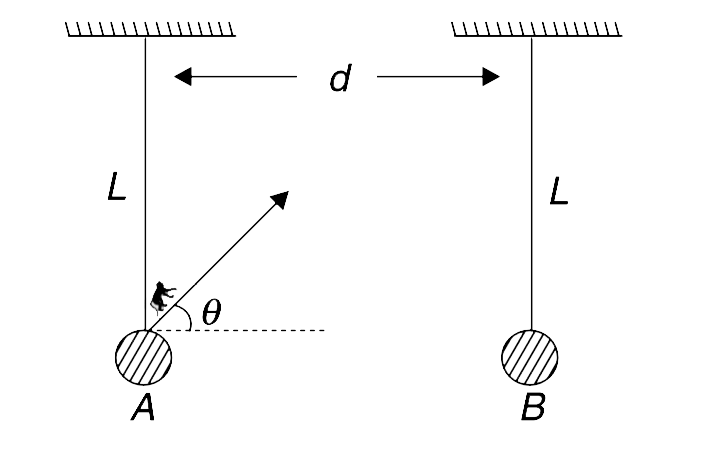
View SolutionVertical strings of same length `L` support two balls A and B of mass `2m` each. There is a small monkey of mass `m` sitting on ball A. Suddenly, the monkey jumps off the ball A at an angle `theta = 45^(@)` to the horizontal and lands exactly on the ball B. Thereafter, the monkey and the ball B just manage to complete the vertical circle.
(a) Find distance d between the two string and the speed with which the monkey jumped of the ball A.
(b) Find the impulse of the string tension on ball A during the small period when the monkey interacted with the ball to jump off it.
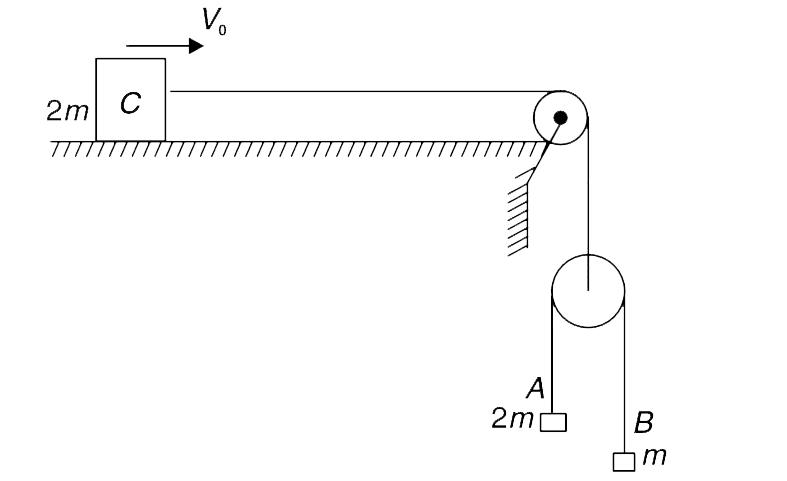
View SolutionIn the shown figure, pulleys and strings are ideal and horizontal surface is smooth. The block C (mass 2m) is given a horizontal velocity of `V_(0) = 3 m//s` towards right and the entire system is let go. Find the velocity of three blocks, just after the strings regain tension. Mass of A and B are `2m and m` respectively and take `g = 10 m//s^(2)`.
View SolutionTwo identical small balls are interconnected with a light and inextensible thread having length L. The system is on a smooth horizontal table with the thread just taut. Each ball is imparted a velocity `v`, one towards the other ball and the other in a direction that is perpendicular to the velocity given to the first ball.
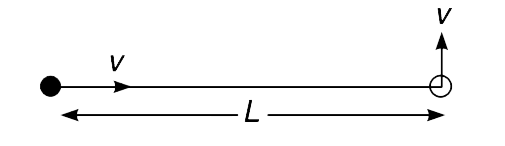
(a) After how much time the thread will become taut again?
(b) Calculate the kinetic energy of the system after the string gets taut.
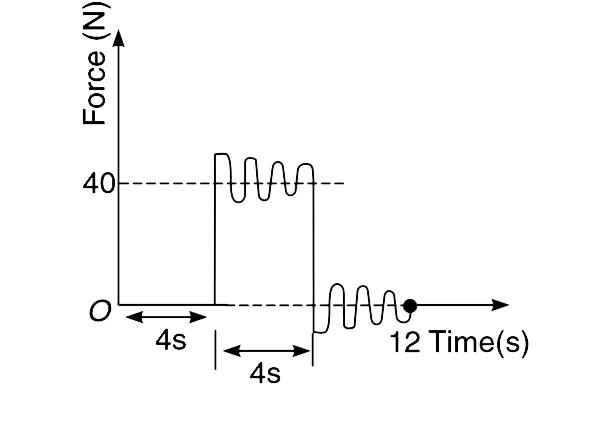
View SolutionA particle of mass `1 kg` is moving with a velocity of 200 m/s. An impulsive force of 4 s duration acts on the particle in a direction opposite to its motion. The force fluctuates a little bit around 40 N magnitude and then it dies out in next 4s showing small fluctuations. An oscilloscope records the force as shown. The two oscillating components in the graph are identical except that one is mirror image of the other. Find the magnitude of velocity of particle after the force stops acting.
View SolutionA moving particle of mass m collides elastically with a stationary particle of mass `2m`. After collision the two particles move with velocity `vec(v)_(1)` and `vec(v)_(2)` respectively. Prove that `vec(v)_(2)` is perpendicular to `(2 vec(v)_(1) + vec(v)_(2))`
View SolutionTwo identical carts are moving on parallel smooth tracks with velocities `u_(1) = 10 ms^(-1) and u_(2) = 15 ms^(-1)`. The empty carts (with drivers) have mass `3m` each. Each cart has a sack of mass m kept at end A and end D (see figure). At the instant the carts being to cross, the sack in cart 1 is the thrown perpendicular (relative to cart 1) with some unknown velocity and it lands on cart 2 at its end D after a time `t_(0)`. Immediately after the sack lands into cart 2, the original sack in cart 2 is thrown perpendicularly (relative to cart 2) towards cart 1 in identical fashion. The sack lands on cart 1 at point M, a time `t_(0)` after the throw. Assume that the carts are constrained to move in straight lines.
(i) Find length BM if length of each cart is L
(ii) Find the velocity of cart 1 after the sack thrown from cart 2 lands on it.
View SolutionA man of mass m is standing on the flat top of a cart of mass `2m`. The length and height of the cart is `L and H` respectively and it is at rest on a smooth horizontal ground. The man starts running from end A, speeds up and jumps out of the cart at point B with a velocity `u` relative to the cart in horizontal direction. Calculate the total horizontal distance covered by the man by the time he lands on the ground.
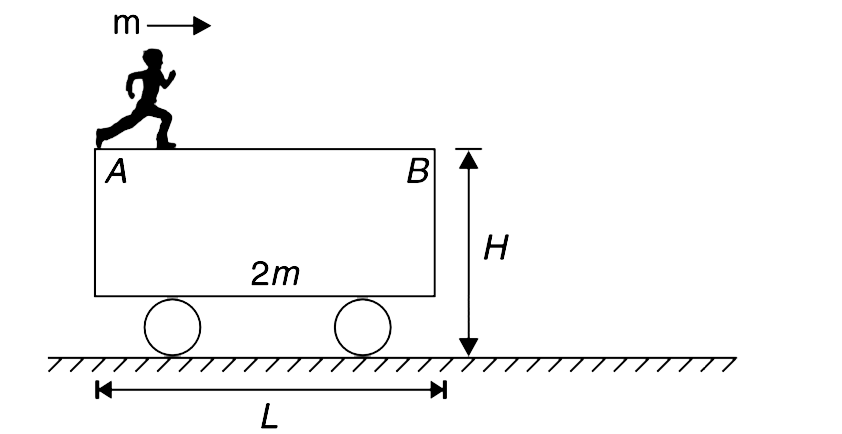
View SolutionTwo blocks of masses `m = 2 kg and m = 8 kg` are connected to a spring of force constant `K = 1 kN//m`. The spring is compressed by `20 cm` and the two blocks are held in this position by a string. The system is placed on a horizontal smooth surface and given a velocity `u = 3 m//s` perpendicular to the spring. The string snaps while moving. Find the speed of the block of mass m when the spring regains its natural length.
View SolutionTwo blocks of mass `M` and `2M` are connected to the two ends of a light, inextensible string passing over an ideal pulley as shown in figure. The system is released from rest.
(a) One second after the system is released, a particle of mass M hits the block of mass M and sticks to it. The particle hits the block with a speed of 10 m/s while travelling downward. Find the total distance travelled by block of mass 2M after it is released.
(b) One second after the system is released, a particle of mass 2M hits the block of mass M and sticks to it. The particle hits the block with a speed of 10 m/s while travelling in upward direction. Find distance travelled by the block of mass 2M after it is released to the time it comes to rest for the first time `(g = 10 m//s)^(2)`
View SolutionA toy car of mass `2 m` is at rest on a smooth horizontal surface. A small bob of mass m is suspended by a mass less string of length L from the roof of the car. A horizontally flying bullet of mass m enters into the car through a small window and sticks to the bob. Speed of the bullet is u. Find minimum value of u (call it `u_(0)`) for which the bob can touch the roof of the car

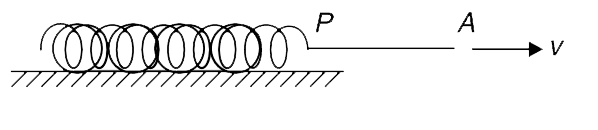
View SolutionA heap of rope is lying on a horizontal surface. One free end A of the rope is pulled horizontally with a constant velocity `v`. Assume that the heap does not move and the moving part of the rope remains straight and horizontal (i.e. there is no sag). Mass per unit length of the rope is `lamda`. Find the tension at point P where the straightened part of the rope meets the heap. How much force the external agent must apply at end A ?
View SolutionA smooth rope of mas `m` and length `L` lies in a heap on a smooth horizontal floor, with one end attached to a block of mass `M`. The block is given a sudden kick and instantaneously acquires a horizontal velocity of magnitude `V_(0)` as shown in figure 1. As the block moves to right pulling the rope from heap, the rope being smooth, the heap remains at rest. At the instant block is at a distance `x` from point `P` as shown in figure `-2( P` is a point on the rope which has just started to move at the given instant `)`, choose correct options for next three question.

The speed of block of mass `M` is
View Solution(i) Three balls 1, 2 and 3 lie on a smooth horizontal table. Ball 1 is given a velocity towards ball 2. Kinetic energy given to ball 1 is `k_(0)`. It collides with 2 and in turn ball 2 hits ball 3. All collisions are head on elastic. Masses of the balls are m, M and m respectively.
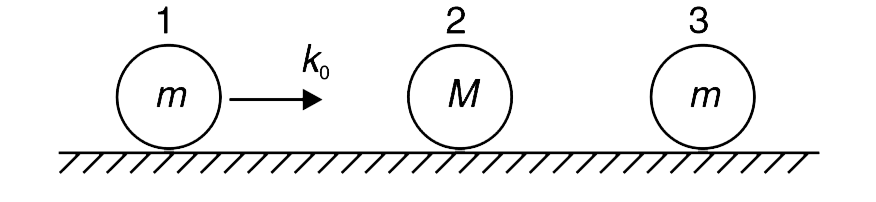
(a) Calculate the kinetic energy `(k_3)` of ball 3 after ball 2 hits it.
(b) Draw the variation of `k_(3)` as a function of M.
(ii) Consider 10 balls laid on a smooth surface with masses `m,(m)/(2),(m)/(4),(m)/(8)......(m)/(512)` and first ball is pushed towards the second with kinetic energy `k_(0)`. [All collisions are elastic and head on]. The kinetic energy acquired by the last ball is `k_(10)`. In a separate experiment the `10^(th)` ball is pushed towards `9^(th)` ball with kinetic energy `k_(0)`. This time the kinetic energy acquired by `1^(st)` ball is `k_(1)`.
Compare `k_(10) and k_(1)`

View SolutionA simple pendulum is suspended from a peg on a wall which is inclined at an angle of `30^(@)` with the vertical. The pendulum is pulled away from the wall to a horizontal position (with string just taut) and released. The bob repeatedly bounces off the wall, the coefficient of restitution being `e = (2)/(sqrt(5))`
Find the number of collisions of the bob with the wall, after which the amplitude of oscillation (meaured from the wall) becomes less than `30^(@)`

View SolutionTwo particles A and B, having same mass m are tied to a common point of suspension O. A is tied with the help of an inextensible string of length L and B is tied using an elastic string of unstretched length `(L)/(2)` . The two particles are released from horizontal positions as shown in figure. The particles have been released at a time gap so that both the string and the elastic cord become vertical simultaneously. It was observed that the length of the cord became equal to that of the string at this moment and the two particles collided. The particles got stuck together and their velocity just after the collision was observed to be `(sqrt(gL))/(2)`.
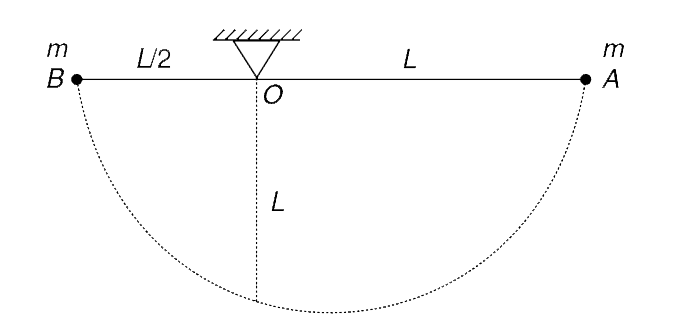
(a) In which direction will the combined mass move immediately after collision – right or left ?
(b) Find tension in the string immediately after the collision.
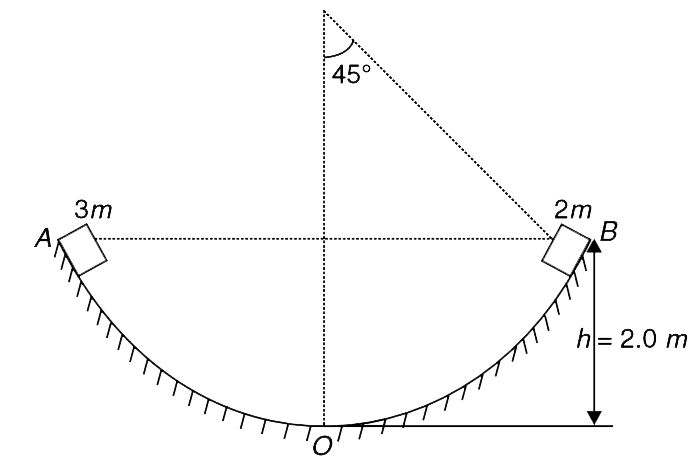
View SolutionA smooth track, fixed to the ground, is in the shape of a quarter of a circle. Two small blocks of mass `3m and 2m` are released from the two edges `A and B` of the circular track. The masses slide down and collide at centre O of the track. Vertical height of A and B from O is `h = 2m`. Collision is elastic. Find the maximum height (above O) attained by the block of mass 2m after collision
View SolutionA man stands on a frictionless horizontal ground. He slides a 10 kg block on the surface with a speed of 3 m/s relative the ground, towards a vertical massive wall. The wall itself it moving towards the man at a constant speed of 2 m/s. The block makes a perfectly head on elastic collision with the wall, rebounds and reaches back to the man 3 second after the throw. At the moment the block was thrown, the wall was at a distance of 10 m from the man.
(a) Find the mass of the man.
(b) Find the ratio of work done by the man in throwing the block to the work done by the wall on the block.
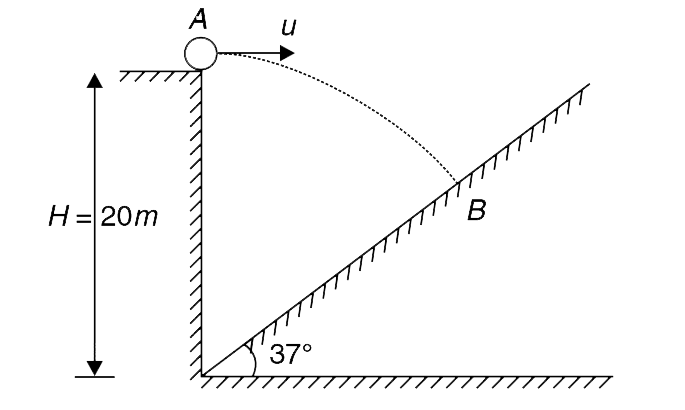
View SolutionA ball is projected from point A in horizontal direction with a velocity of `u = 28 m//s`. It hits the incline plane at point B and rebounds. Show that whatever be the coefficient of restitution between the ball and the incline, the ball will always hit the incline for the second time at a point above B (i.e., it will not hit the incline below B). Assume the incline to be smooth and take `g = 10 m//s^(2) [sin 37^(@)=(3)/(5)]`
View SolutionA staircase has each step of height h and width x. A ball strikes the centre point of a step with velocity `v` making an angle `theta` with the vertical. It rebounds and strikes the centre point of the next step. Once again it rebounds and hits the centre point of the next step and so on.

Assume that there is no friction between the ball and the steps and coefficient of restitution is e.
(a) Show that each time after hitting a step, the ball climbs to the same height (i.e., heights like AB and CD shown in figure are equal).
(b) Find h and x.
View SolutionTwo identical discs are initially at rest in contact on a horizontal table. A third disc of same mass but of double radius strikes them symmetrically and comes to rest after the impact.
(a) Find the coefficient of restitution for the impact.
(b) Find the minimun kinetic energy of the system (as a percentage of original kinetic energy before collision) during the process of collision.
Treat the collision to be instantaneous
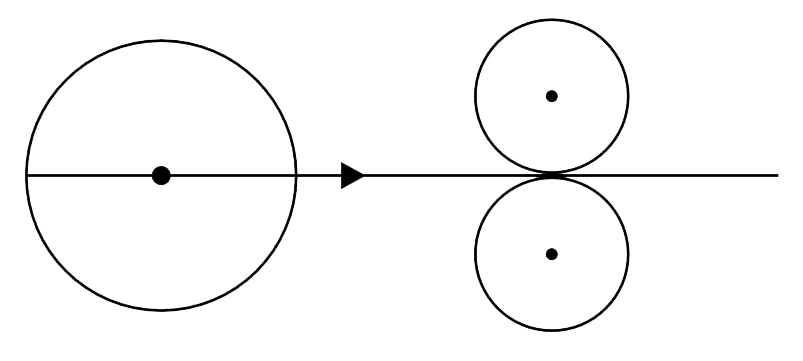
View SolutionOn a billiard table two balls B and C are at rest touching each other. A third ball A, travelling with speed u, strikes the two balls elastically (see fig.). Somehow, A hits B first and within a fraction of a second hits ball C. You may assume that B and C are placed symmetrically with respect to the line of motion of A and that all the balls are identical. What angle does the final velocity of A make with its original direction of motion.
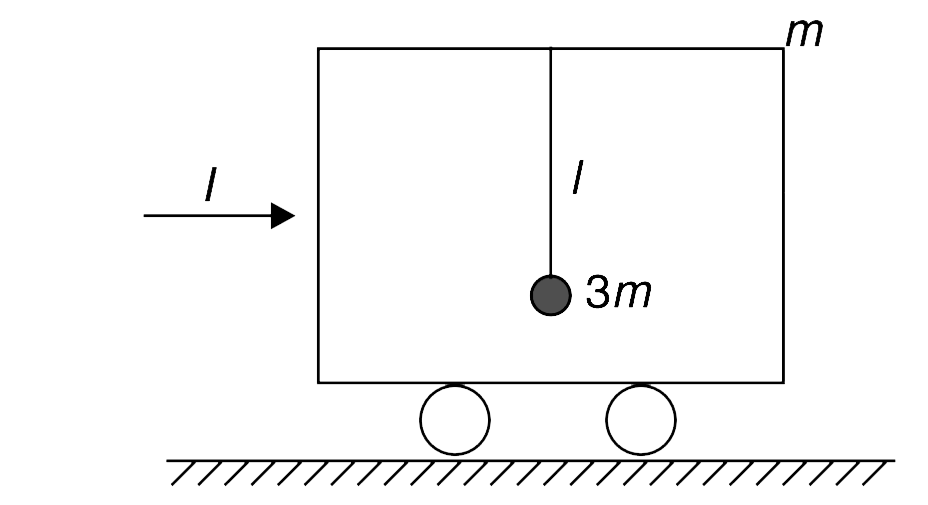
View SolutionA toy car of mass m is placed on a smooth horizontal surface. A particle of mass 3m is suspended inside the car with the help of a string of length `l`. Initially everything is at rest. A sudden horizontal impulse `I = 2m sqrt(gl)` is applied on the car and it starts moving.
(a) Find the maximum angle `q_(0)` that the string will make with the vertical subsequently.
(b) Find tension in the string when it makes angle `theta_(0)` with the vertical.
View SolutionA smooth ball of mass M and radius R is lying on a smooth horizontal table. A smaller ball of radius r and mass m travelling horizontally on the table with velocity u hits the larger ball. Collision is elastic. During the interaction of the balls the larger ball does not lose contact with the table at any instant

(i) Calculate the velocity of the balls after collision.
(ii) Calculate the maximum possible interaction force between the balls during collision.
View SolutionA light rigid rod has a small ball of mass m attached to its one end. The other end is hinged on a table and the rod can rotate freely in vertical plane. The rod is released from vertical position and while falling the ball at its end strikes a hemisphere of mass m lying freely on the table. The collision between the ball and the hemisphere is elastic. The radius of hemisphere and length of the rod are R and 2R respectively. Find the velocity of the hemisphere after collision.
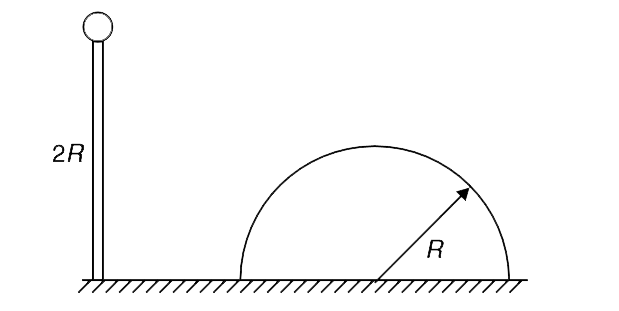
View Solution(i) O is a fixed peg at a height H above a perfectly inelastic smooth horizontal plane. A light inextensible string of length `L (gt H)` has one end attached to `O` and the other end is attached to a heavy particle. The particle is held at the level of O with string horizontal and just taut and released from rest. Find the height of the particle above the plane when it comes to rest for the first time after the release.

(ii) The bob of a pendulum has mass m and the length of pendulum is `l`. It is initially at rest with the string vertical and the point of suspension at a height `2l` above the floor. A particle P of mass `(m)/(2)` moving horizontally along –ve x-direction with velocity `sqrt(2gl)` collides with the bob and comes to rest. The bob swings and when it comes to rest for the first time, another particle Q of mass m moving horizontally along y direction collides with the bob and sticks to it. It is observed that the bob now moves in a horizontal circle.
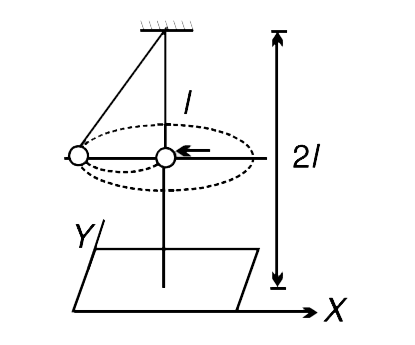
(a) Find tension in string just before the second collision.
(b) Find the height of the circular path above the floor.
(c) Find the time period of the circular motion.
(d) The string breaks during the circular motion at time `t = 0`. At what time the bob will hit the floor ?
View SolutionA billiard ball collides elastically with an identical stationary ball. The collision is not head on. Show that the directions of motion of the two balls are at right angles after the collision. Solve the problem in centre of mass frame as well as in lab frame.
View Solution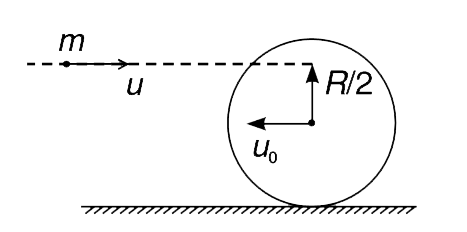
A heavy ball of radius R is travelling on a smooth horizontal surface with a velocity of u0 towards left. A horizontally moving small ball of mass m strikes it at a height `(R)/(2)` above the centre while travelling with velocity u towards right.
(a) After collision the small ball moves in vertically upwards direction with velocity u. Prove that this can happen only if `u gt sqrt(3)u_(0)`
(b) Find the velocity of small ball after collision if the collision is elastic and the balls are smooth.
View SolutionTwo elastic balls of masses M and m `(M gt gt m)` are placed on top of each other with a small gap between them. The balls are dropped on to the ground with the bottom of the lower ball at height h above the ground. The lower ball has a radius R and the upper ball has negligible dimension.
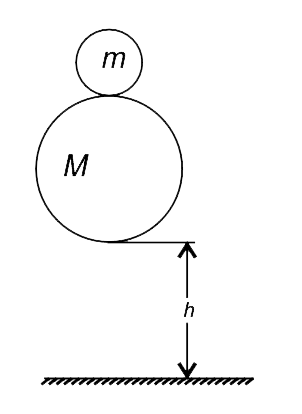
(a) Up to what height the ball of mass m will bounce above the ground ?
(b) Does the result obtained above violates the low of conservation of mechanical energy?
View SolutionThree identical particles are placed on a horizontal smooth table, connected with strings as shown. The particle B is imparted a velocity `V_(0) = 9 m//s` in horizontal direction perpendicular to the line ABC. Find speed of particle A when it is about to collide with C.
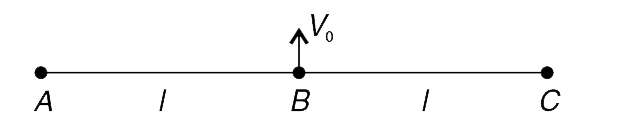
View SolutionA light inextensible string, passing over a pulley, supports two particles 1 and 2 at its ends. An insect of mass m is sitting on particle 2 and the system is in equilibrium. The sum of masses of particles and the insect is M. Now the insect crawls a distance `x` up relative to the string. Find the displacement of centre of mass of the system of two particles and the insect. In which direction does the centre of mass move and why ?
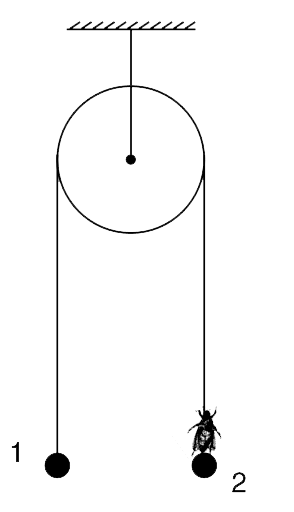
View SolutionTwo particles (A and B) of masses m and 2m are joined by a light rigid rod of length L. The system lies on a smooth horizontal table. The particle (A) of mass m is given a sharp impulse so that it acquires a velocity u perpendicular to the rod. Calculate maximum speed of particle B during subsequent motion. By what angle `theta` will the rod rotate by the time the speed of particle B become maximum for the first time ?

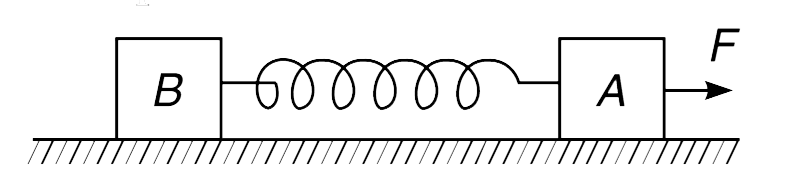
View SolutionTwo blocks A and B, each of mass m, are connected by a spring of force constant K. Initially, the spring is in its natural length. A horizontal constant force F starts acting on block A at time `t=0` and at time t , the extension in the spring is seen to be `l`. What is the displacement of the block A in time `t` ?
View SolutionTwo blocks of mass `m_(1) and m_(2)` are connected to the ends of a spring. The spring is held compressed and the system is placed on a smooth horizontal table. The block of mass `m_(1) = 2 kg` is kept at `x = 1 cm` mark and the other block is at `x = 2 cm` mark. The system is released from this position. It was observed that at the instant `m_(1)` was at `x = 5 cm` mark its velocity was zero and at that moment `m_(2)` was located at `x = -4 cm`. Find mass `m_(2)` and unstretched length `(l_(0))` of the spring

View SolutionTwo particles having masses `m_(1) and m_(2)` are moving with velocities `vec(V)_(1) and vec(V)_(2)` respectively. `vec(V)_(0)` is velocity of centre of mass of the system.
(a) Prove that the kinetic energy of the system in a reference frame attached to the centre of mass of the system is `KE_(cm) = (1)/(2)mu V_(rel)^(2)`. Where `mu=(m_(1)m_(2))/(m_(1)+m_(2))` and `V_(rel)` is the relative speed of the two particles.
(b) Prove that the kinetic energy of the system in ground frame is given by
`KE=KE_(cm)+(1)/(2)(m_(1)+m_(2))V_(0)^(2)`
(c) If the two particles collide head on find the minimum kinetic energy that the system has during collision.
View SolutionTwo blocks A and B of mass m and `2m` respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo ring of mass m and `2m` are connected with a light spring and can slide over two frictionless parallel horizontal rails as shown in figure. Ring of mass m is given velocity `'v_(0)'` in horizontal direction as shown. Calculate the maximum stretch in spring during subsequent motion.

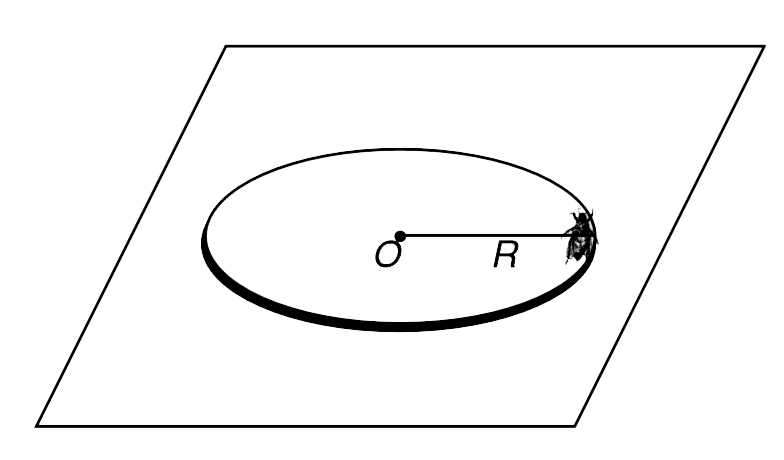
View SolutionA disc of mass M and radius R is kept flat on a smooth horizontal table. An insect of mass m alights on the periphery of the disc and begins to crawl along the edge.
(a) Describe the path of the centre of the disc.
For what value of `(m)/(M)` the centre of the disc and the insect will follow the same path ?
View SolutionA metal wire having mass M is bent in the shape of a semicircle of radius R and is sliding inside a smooth circular grove of radius R present in a horizontal table. The wire just fits into the groove and is moving at a constant speed V. Find the magnitude of net force acting on the wire.

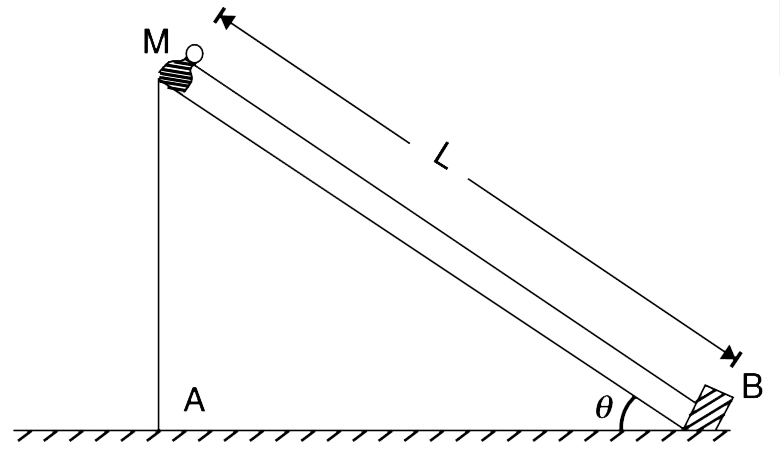
View SolutionA triangular wedge (A) has inclined surface making an angle `theta = 37^(@)` to the horizontal. A motor (M) is fixed at the top of the wedge. Mass of the wedge plus motor system is 3m. A small block (B) of mass `m = 1kg` is placed at the bottom of the incline and is connected to the motor using a light string. The motor is switched on and it slowly hauls block B through a distance `L = 2.0` meter along the incline. Calculate the work done by the string tension force on the wedge plus motor system. All surfaces are frictionless.
View SolutionAn ice cream cone of mass M has base radius R and height `h`. Assume its wall to be thin and uniform. When ice cream is filled inside it (so as to occupy the complete conical space) its mass becomes `5 M`. Find the distance of the centre of mass of the ice cream filled cone from its vertex.
View SolutionA flexible rope is in the shape of a semicircle ACB with its centre at O. Ends A and B are fixed. Radius of the semicircle is R. The midpoint C is pulled so that the rope acquires V shape as shown in the figure.
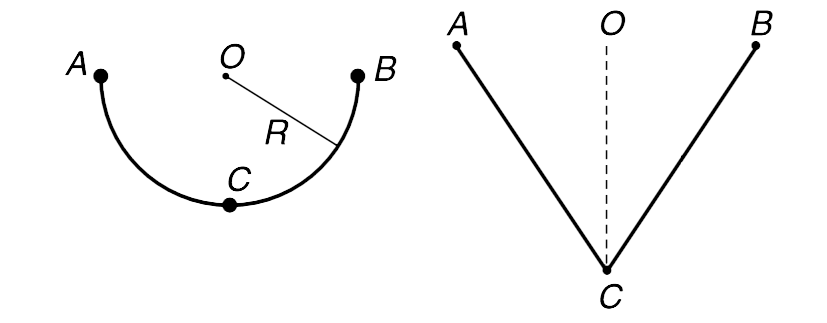
(a) Make a guess whether the centre of mass of the rope moves closer to O or moves away from it when it is pulled?
(b) Calculate the shift in position of the centre of mass of the rope.
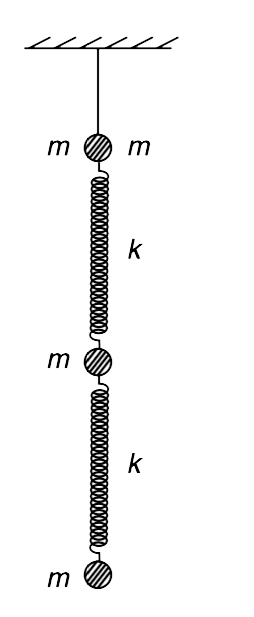
View SolutionThree small balls of equal mass (m) are suspended from a thread and two springs of same force constant (K) such that the distances between the first and the second ball and the second third ball are the same. Thus the centre of mass of the whole system coincides with the second ball. The thread supporting the upper ball is cut and system starts a free fall. Find the distance of the centre of mass of the system from the second ball when both the springs acquire their natural length in the falling system.
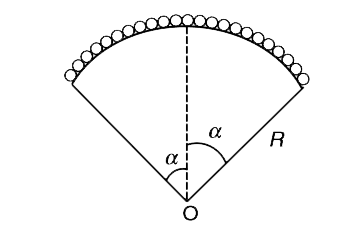
View Solution(a) A uniform chain is lying in form of on arc of a circle of radius R. The arc subtends an angle of `2 alpha` at the centre of the circle. Find the distance of the centre of mass of the chain from the centre of the circle.
(b) A uniform chain of length `(piR)/(2)` is lying symmetrically on the top of a fixed smooth half cylinder (see figure) of radius R. The chain is pulled slightly from one side and released. It begins to slide. Find the speed of the chain when its one end just touches the floor. What is speed of centre of mass of the chain at this instant ?
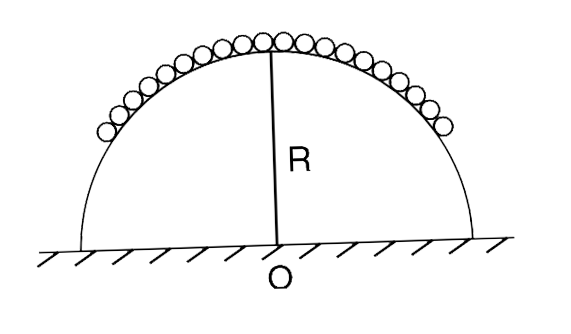
(c) In part (b) assume that the half cylinder is not fixed and can slide on the smooth floor. Find the displacement of the cylinder by the time one end of the chain touches the floor. Mass of cylinder is equal to that of the chain. For part (b) and (c) assume that the chain remains in contact with the cylinder all the while.
View SolutionA small body of mass m is at rest inside a narrow groove carved in a disc. Groove is a circle of radius R concentric to the disc. Mass of the disc is also m . The disc lies on a smooth horizontal floor. The small body is given a sharp impulse so that it acquires a tangential velocity Vo at time t = 0.

(a) The velocity of the centre of the disc becomes zero for the first time at time `t_(0)`. Find `t_(0)`
(b) Find speed of the small body at time `(t_(0))/(3)`
View SolutionLaila and Majnu are on a boat for a picnic. The boat is initially at rest. Laila has a big watermelon which she throws towards Majnu. The man catches the melon and eats half of it. He throws back the remaining half to Laila. She eats the half of the melon that she receives & throws the remaining part to Majnu. Majnu again eats half of what he receives and returns the remaining part back to Laila. This continues till the melon lasts. The two are sitting at the two ends of the boat which has a length L. Combined mass of the boat and the two lovers is `M_(0)` and the mass of the water melon is M. Assume that the boat can move horizontally on water without any resistive force. Find the displacement of the boat when the watermelon gets finished.

View SolutionA hot air balloon (mass M) has a passenger (mass m) and is stationary in the mid air. The passenger climbs out and slides down a rope with constant velocity u relative to the balloon.
(a) Show that when the passenger is sliding down, there is no change in mechanical energy (kinetic + gravitational potential energy) of the system (Balloon + passenger). Calculate the speed of balloon.
(b) Calculate the power of the buoyancy force on the system when the man is sliding. For easy calculation, assume that volume of man is negligible compared to the balloon.
(c) If buoyancy force is doing positive work, where is this work done lost? You have proved that sum of kinetic and potential energy of the system remains constant
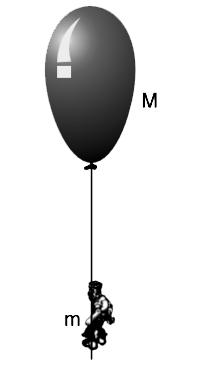
View Solution
Momentum And Center of Mass questions and complete solutions for chapter MOMENTUM AND CENTRE OF MASS of ARIHANT PHYSICS (HINGLISH) of Class 11