Complete Solutions to UISCOSITY of chapter VISCOSITY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | VISCOSITY |
| ARIHANT MASTER PROBLEM | UISCOSITY |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
During a painting process, a thin, flat tape of width b (dimension perpendicular to the plane of the figure) is pulled through a paint filled channel of length L. The density and viscosity of the paint liquid is `rho` and `eta` respectively. The tape is pulled at a constant speed v and width of the channel is h. Find the minimum force needed to pull the tape.

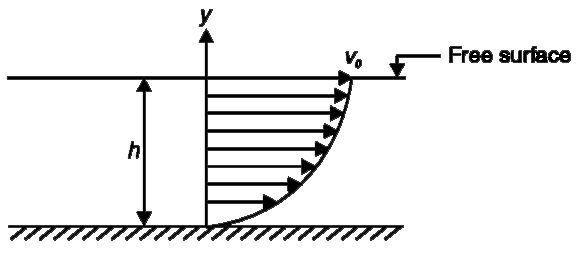
View SolutionA liquid is flowing through a horizontal channel. The speed of flow (v) depends on height (y) from the floor as `v=v_(0)[2((y)/(h))-((y)/(h))^(2)]`.Where h is the height of liquid in the channel and `v_(0)` is the speed of the top layer. Coefficient of viscosity is `eta`. Calculate the shear stress that the liquid exerts on the floor.
View SolutionA car having cross sectional area of its front equal to A is travelling on a highway at a speed v. The viscous drag force acting on the car is known to be given as `F_(v)=CArhov^(2)` .Where `rho` is density of air and C is a constant which depends on the shape of the car. The petrol used by the car produces E joules of energy per kg of it burnt. Calculate the mileage (in km/kg) of the car if the combined efficiency of its engine and transmission is f.
View SolutionAn ideal fluid flows through a pipe of circular cross section of radius r at a speed `v_(0)`. Now a viscous liquid is made to flow through the pipe at the same volume flow rate (measured in `m^(3)s^(–1)`). Find the maximum speed of a fluid particle in the pipe.
View SolutionA near surface earth satellite is in the shape of a sphere of radius r. It encounters cosmic dust in its path. The viscous force experienced by the satellite follows stoke’s law. The coefficient of viscosity is `eta`. Mass and radius of the earth are M and R respectively. (a) Calculate the power of the rocket engine that must be put on to keep the satellite moving as usual. (b) Calculate the equilibrium temperature of the surface of the satellite assuming that it radiates like a black body and no outer radiation falls on it. Assume that the heat generated due to viscous force is absorbed completely by the satellite body.
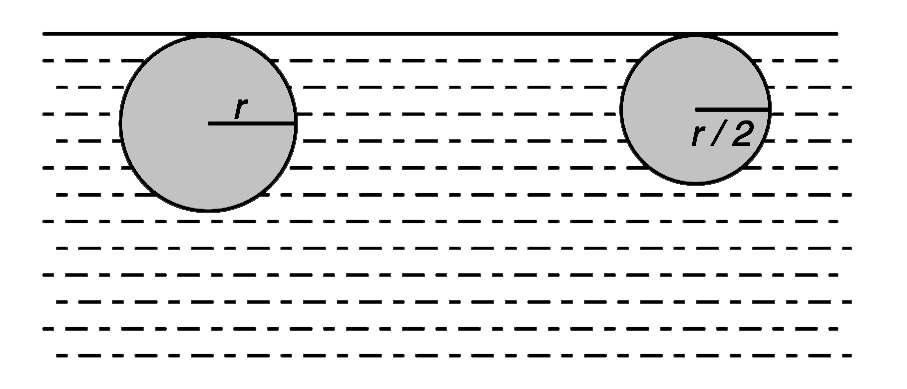
View SolutionTwo balls of radii r and `(r)/(2)` are released inside a deep water tank. Their initial accelerations are found to be `(g)/(2)` and `(g)/(4)` respectively. Find the velocity of smaller ball relative to the larger ball, a long time after the two balls are released. Coefficient of viscosity is given to be `eta`.
View SolutionThe coefficient of viscosity `eta` of a gas depends on mass of the gas molecule, its effective diameter and its average speed. It is known that diameter of helium atom is `2.1xx10^(-10)` m and its coefficient of viscosity, at room temperature is `2.0 xx 10^(-5)` kg `m^(-1)s^(-1)`. Estimate the effective diameter of `CO_(2)` molecule if it is known that `eta` at room temperature for `CO_(2)` is `1.5 xx 10^(-5)` kg `m^(-1)s^(-1)`.
View SolutionWhen hard brakes are applied (so as to lock the wheels) in a car travelling on a wet road it can “hydro-plane”. A film of water is created between the tires and the road and, theoretically, the car can slide a very long distance. [In practice film is destroyed much before such distances can be achieved]. Consider a car of mass M moving on a wet road with speed `v_(0)`. Hard brakes are applied. Let the area of film under all four tires be A and thickness of the film be h. Coefficient of viscosity is `eta`.
(a) Calculate the distance (x) to which the car will slide before coming to rest.
Calculate the value of x for `M=10^(3)`kg, `A=0.2 m^(2), h=0.1` mm, `v_(0)=20ms^(-1)`, and `eta=10^(-3)`kg `m^(-1)`
View SolutionA spherical ball of radius r and density d is dropped from rest in a viscous fluid having density `rho` and coefficient of viscosity `eta`.
(a) Calculate the power `(P_(1))` of gravitational force acting on the ball at a time t after it is dropped. (b) Calculate the rate of heat generation `(P_(2))` due to rubbing of fluid molecules with the ball, at time t after it is dropped. (c) How do `P_(1)` and `P_(2)` change if the radius of the ball were doubled? (d) Find `P_(1)` and `P_(2)` when both become equal.
View SolutionTwo balls of same material of density `rho` but radius `r_(1)` and `r_(2)` are joined by a light inextensible vertical thread and released from a large height in a medium of coefficient of viscosity `= eta`. Find the terminal velocity acquired by the balls. Also find the tension in the string connecting both the balls when both of them are moving with terminal velocity. Neglect buoyancy and change in acceleration due to gravity.
View SolutionA car windshield wiper blade sweeps the wet windshield rotating at a constant angular speed of `omega`. R is the radius of innermost arc swept by the blade. Length and width of the blade are l and b respectively. Coefficient of viscosity of water is `eta`. Calculate the torque delivered by the motor to rotate the blade assuming that there is a uniform layer of water of thickness t on the glass surface.

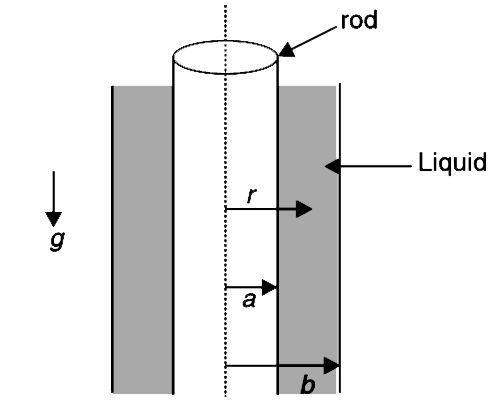
View SolutionA vertical steel rod has radius a. The rod has a coat of a liquid film on it. The liquid slides under gravity. It was found that the speed of liquid layer at radius r is given by
`v=(rhogb^(2))/(2eta)ln((r)/(a))-(rhog)/(4eta)(r^(2)-a^(2))`
Where b is the outer radius of liquid film, `eta` is coefficient of viscosity and `rho` is density of the liquid.
(i) Calculate the force on unit length of the rod due to the viscous liquid?
(ii) Set up the integral to calculate the volume flow rate of the liquid down the rod. [you may not evaluate the integral]
View SolutionA viscometer (an instrument used to study characteristics of a non-ideal fluid) consists of a flat plate and a rotating cone. The cone has a large apex angle and the angle `theta` shown in figure is very small (typically less than `0.5^(@)` ). The apex of the cone just touches the plate and a liquid fills the narrow gap between the plate and the cone. The cone has a base radius R and is rotated with constant angular speed `omega`. Consider the liquid to be ideal and take its coefficient of viscosity to be `eta`. Calculate the torque needed to drive the cone.

View Solution
UISCOSITY questions and complete solutions for chapter VISCOSITY of ARIHANT PHYSICS (HINGLISH) of Class 11