A liquid is flowing through a horizontal channel. The speed of flow (v) depends on height (y) from the floor as v=v0[2(yh)−(yh)2].Where h is the height of liquid in the channel and v0 is the speed of the top layer. Coefficient of viscosity is η. Calculate the shear stress that the liquid exerts on the floor.
![A liquid is flowing through a horizontal channel. The speed of flow (v) depends on height (y) from the floor as v=v(0)[2((y)/(h))-((y)/(h))^(2)].Where h is the height of liquid in the channel and v(0) is the speed of the top layer. Coefficient of viscosity is eta. Calculate the shear stress that the liquid exerts on the floor.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C10_E01_002_Q01.png)
Step by step video & image solution for A liquid is flowing through a horizontal channel. The speed of flow (v) depends on height (y) from the floor as v=v_(0)[2((y)/(h))-((y)/(h))^(2)].Where h is the height of liquid in the channel and v_(0) is the speed of the top layer. Coefficient of viscosity is eta. Calculate the shear stress that the liquid exerts on the floor. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
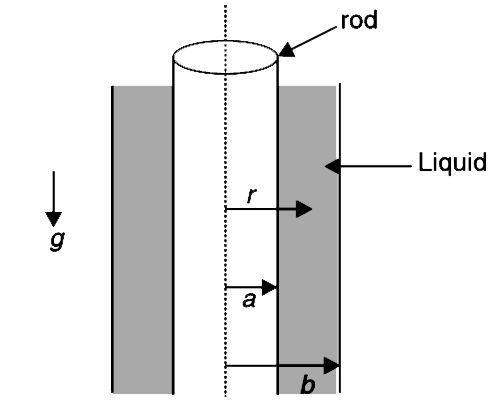
A vertical steel rod has radius a. The rod has a coat of a liquid film on it. The liquid slides under gravity. It was found that the speed of liquid layer at radius r is given by
v=ρgb22ηln(ra)−ρg4η(r2−a2)
Where b is the outer radius of liquid film, η is coefficient of viscosity and ρ is density of the liquid.
(i) Calculate the force on unit length of the rod due to the viscous liquid?
(ii) Set up the integral to calculate the volume flow rate of the liquid down the rod. [you may not evaluate the integral]
View SolutionCheck the accuracy of the relation η=π8Pr4lV
Here, P is pressure, V= rate of flow of liquid through a pipe, η is coefficient of viscosity of liquid.
View Solution
Knowledge Check
A liquid is flowing through a horizontal channel. The speed of flow (v) depends on height (y) from the floor as v=v0[2(yh)−(yh)2]. Where h is the height of liquid in the channel and v0 is the speed of the top layer. Coefficient of viscosity is η. Then the shear stress that the liquid exerts on the floor is.
A2ηv0hB3ηv0hC4ηv0hD2ηv03hAn incompressible liquid is flowing through a horizontal pipe as shown in figure. The value of speed v is
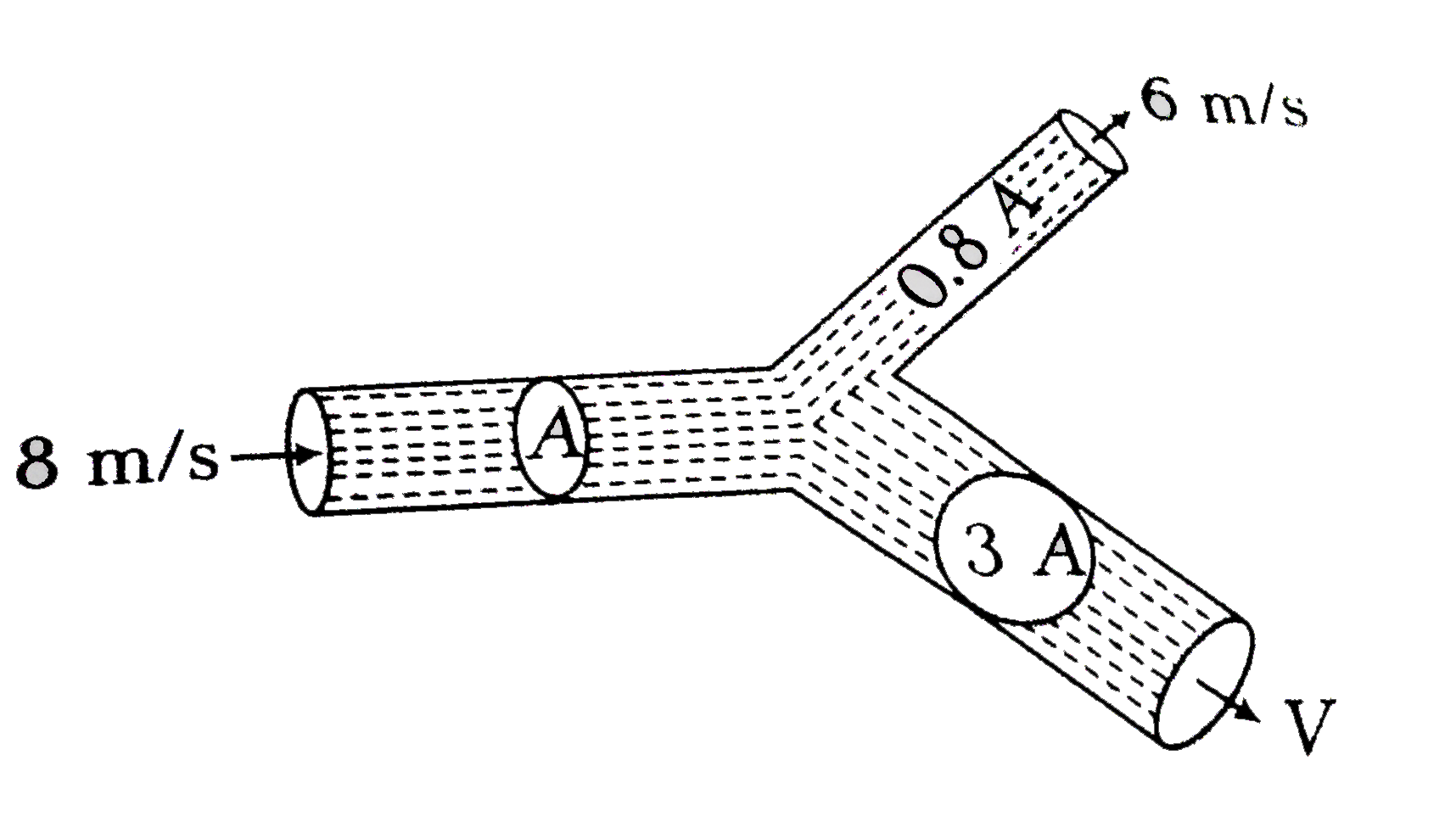 A1.1ms−1B2.1ms−1C3.1ms−1D5.1ms−1
A1.1ms−1B2.1ms−1C3.1ms−1D5.1ms−1A body is thrown from a height h with speed, u it hits the ground with speed v
Athe value of v is minimum if the body is thrown horizontallyBthe value of v is maximum if the body is thrown vertically upwardsCthe value of v is maximum if the body is thrown vertically downwardsDThe value of v does not depend on the direction in which it is thrown
If V1 and V2D be the volumes of the liquids flowing out of the same tube in the same interval of time and η1 and η2 their coefficients of viscosity respectively then
View SolutionA liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then

View SolutionA liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h, then

View SolutionA tube of length 1 and radius R carries a steady flow of fluid whose density is ρ and viscosity η. The velocity v of flow is given by v=v0(1−r2/R2) Where r is the distance of flowing fluid from the axis.
View SolutionWhen a liquid flows in a tube, there is relative motion between adjacent layers of the liquid. This force is called the viscous force which tends to oppose the relative motion between the layers of the liquid. Newton was the first person to study the factors that govern the viscous force in a liquid. According to Newton’s law of viscous flow, the magnitude of the viscous force on a certain layer of a liquid is given by
F=−ηAdvdx
where A is the area of the layer dvdx is the velocity gradient at the layer and η is the coefficient of viscosity of the liquid.
A river is 5 m deep. The velocity of water on its surface is 2ms−1 If the coefficient of viscosity of water is 10−3Nsm−2 , the viscous force per unit area is :
View Solution