Complete Solutions to Solved Example of chapter CHEMICAL EQUILIBRIUM of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | CHEMICAL EQUILIBRIUM |
| CENGAGE CHEMISTRY | Solved Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Which graph will show equilibrium condition?
View SolutionFor `A+BhArrC+D` , the equilibrium constant is `K_(1)` and for `C+DhArrA+B`, the equilibrium constant is `K_(2)`. The correct relation between `K_(1)` and `K_(2)` is
View SolutionFor the reactions,
`AhArrB, K_(c)=1,BhArrC,K_(c)=3,ChArrD,K_(c)=5`. `K_(c)` for the reaction `AhArrD` is
View SolutionThe law of mass action was enunciated by
View SolutionAt a certain temperature , the following reactions have the equilibrium constants as shown below:
`S(s)+O_(2)(g)hArrSO_(2)(g),K_(c)=5xx10^(52)`
`2S(s)+3O_(2)(g)hArr2SO_(3)(g),K_(c)=10^(29)`
what is the equilibrium constant `K_(c)`for the reaction at tahea same temperature?
`2SO_(2)(g)+O_(2)(g)hArr2SO_(3)(g)`
View SolutionWhen `4 mol` of `A` is mixed with `4 mol` of `B, 2 mol` of `C` and `D` are formed at equilibrium, according to the reaction
`A+B hArr C+D`
the equilibrium constant is
View SolutionThe rate at which a substance reacts, depends on its:
View SolutionThe state of equilibrium refers to
View SolutionFor the reaction, `A+2B hArr C`, the expession for equilibrium constant is
View SolutionFor the reaction:
`2A(g)+B(g) hArr 3C(g)+D(g)`
Two moles each of `A` and `B` were taken into a flask. The following must always be true when the system attained equilibrium
View SolutionIn aa chemical reaction equilibrium is established when :
View SolutionActive mass is defined as
View SolutionFor the reaction
`N_(2)+3H_(2)hArr2NH_(3)`
and `(1)/(2)N_(2)+(3)/(2)H_(2)hArrNH_(3)`
write down the expression for equilibrium constants `K_(c )` and `K_(c )^(')`. How is `K_(c )` related to `K_(c )^(')`?
View SolutionThe equilibrium constant for the reaction
`N_(2)+2O_(2)hArr2NO_(2)`
at a particular temperature is `100`. Write down the equilibrium law equations for the following reaction and determine the values of equilibrium constants.
`2NO_(2)hArrN_(2)+2O_(2)`
`NO_(2)hArr1//2N_(2)+O_(2)`
View SolutionDetermine `K_(c )` for the reaction
`(1)/(2)N_(2)(g)+(1)/(2)O_(2)(g)+(1)/(2)Br_(2)(g)hArrNOBr(g)`
from the following data at `298 K`.
The equilibrium constants for the following reaction
`2NO(g)hArrN_(2)(g)+O_(2)(g)`
and `NO(g)+(1)/(2)Br_(2)(g)hArrNOBr(g)`
are `2.4xx10^(30)` and `1.4`, respectively.
View SolutionFor the hypothetical reactions, the equilibrium constant `(K)` value are given
`AhArrB,K_(1)=2,BhArrC,K_(2)=4,`
`ChArrD,K_(3)=3`
The equilibrium constant (K) for the reaction
`AhArrD` is
View SolutionConsider the following gases equilibrium given below:
(i) `N_(2)+3H_(2)hArr2NH_(3),"Eqm.Constant"=K_(1)`
(ii)`N_(2)+O_(2)hArr2NO, Eqm.constant=K_(2)`
(III) `H_(2)+(1)/(2)O_(2)hArrH_(2)O,Eqm.constant=K_(3)`
The equilibrium constant for the reaction ,`2NH_(3)+(5)/(2)O_(2)hArr3H_(2)O"in terms of" K_(1),K_(2)andK_(3)`will be :
View SolutionIn areversible reaction, study of its mechanism says that both the forward and reverse reaction follows first-order kinetics. If the halflife of forward reaction `(t_(1//2))_(f)` is `400 s` and that of reverse reaction `(t_(1//2))_(b)` is `250 s`, the equilibrium of the reaction is
View SolutionA vessel at `1000 K` contains carbon dioxide with a pressure of `0.5 atm`. Some of the carbon dioxide is converted to carbon monoxide on addition of graphite. Calculate the value of `K_(p)` if total pressure at equilibrium is `0.8 atm`.
View SolutionA sample of `CaCO_(3)(s)` is introduced into a sealed container of volume `0.654 L` and heated to `1000 K` until equilibrium is reached. The equilibrium constant for the reaction
`CaCO_(3)(s)hArrCaO(s)+CO_(2)(g),`
is `3.9xx10^(-2)` atm at this temperature. Calculate the mass of `CaO` present at equilibrium.
View SolutionForm the given data of equilibrium constants of the following reactions:
`CuO(s)+H_(2)(g)hArrCu(s)+H_(2)O(g),K=67`
`CuO(s)+CO(g)hArrCu(s)+CO_(2)(g),K=490`
Calculate the equilibrium constant of the reaction,
`CO_(2)(g)+H_(2)(g)hArr+CO(g)+H_(2)O(g)`
View SolutionGiven that at `1000 K`
`2SO_(2)(g)+O_(2)(g)hArr2SO_(3)(g),K=261`
Calculate K for the following equations:
a. `2SO_(3)(g)hArr2SO_(2)(g)+O_(2)(g)`
b. `SO_(3)(g)hArrSO_(2)(g)+(1)/(2)O_(2)(g)`
c. `SO_(2)(g)+(1)/(2)O_(2)(g)hArrSO_(3)(g)`
View SolutionIf `N_(2)+3H_(2)overset(K)(hArr)2NH_(3)` then `2N_(2)+6H_(2)overset(K')(hArr)4NH_(3);K'` is equal to
View SolutionEquilibrium constants for four different reaction are given as `K_(1)=10^(6), K_(2)=10^(-4), K_(3)=10`, and `K_(4)=1`. Which reaction will take maximum time to attain equilibrium?
View SolutionIn the equilibrium constant for `AhArr B+C` is `K_(eq)^((1))` and that of `B+C=P` is `K_(eq)^((2))`, the equilibrium constant for `AhArr P` is :
View Solution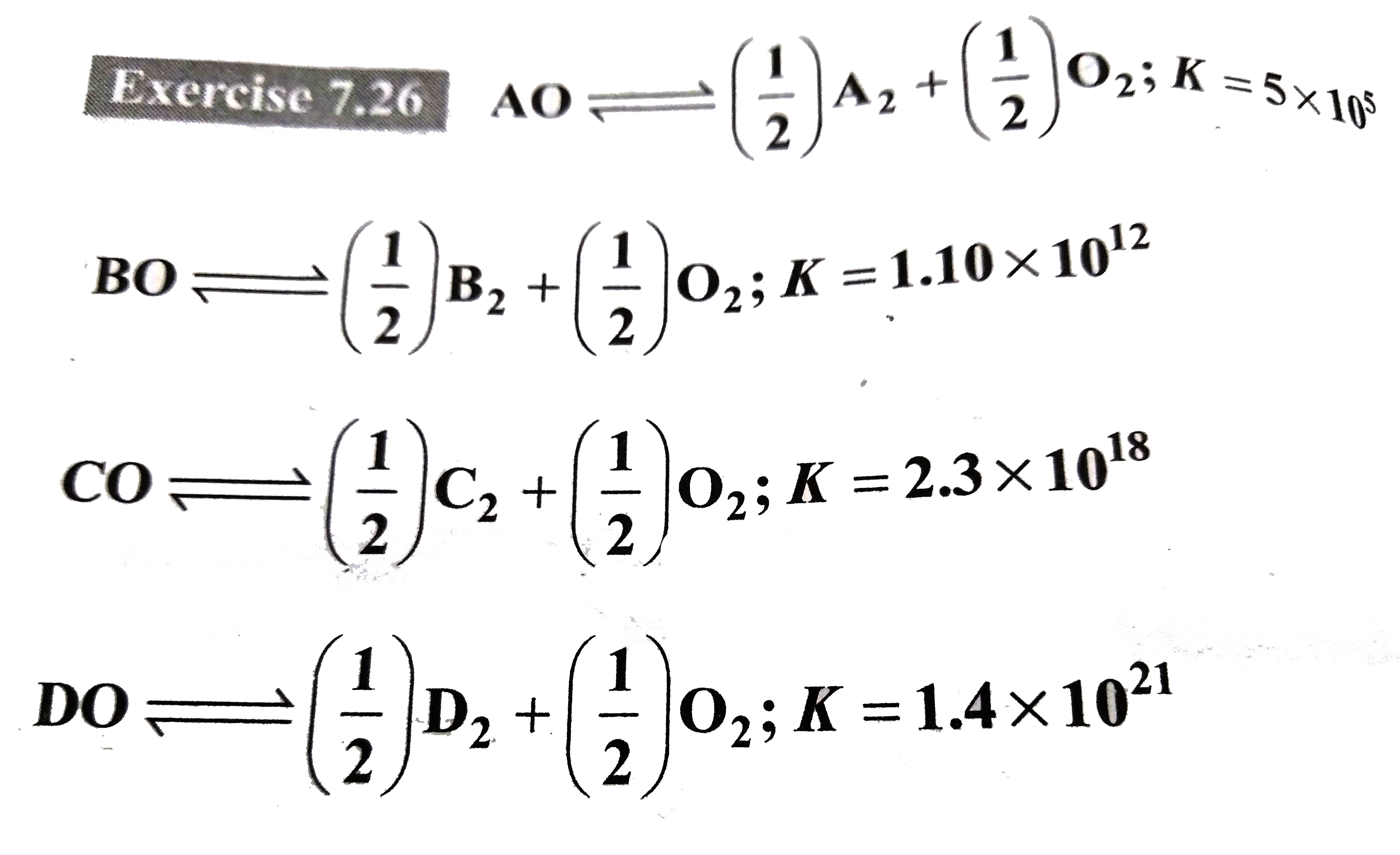
Which oxide is most stable?
View SolutionTheory of 'active mass' indicates that the rate of a chemical reaction is directly proportional to the
View SolutionIn the system `X+2YhArrZ`, the equilibrium concentration are,
`[X]=0.06" mol L"^(-1),[Y]=0.12" mol L"^(-1)`,
`[Z]=0.216" mol L"^(-1)`. Find the equilibrium constant of the reaction.
View SolutionEquilibrium constants `(K)` for the reaction `2NO(g)+Cl_(2)(g)hArr2NOCl(g)` is correctly given by the expression
View SolutionConsider the following equilibrium:
`SO_(2)(g)+(1)/(2)O_(2)(g)overset(K_(1))(hArr)SO_(3)(g),`
`2SO_(3)(g) overset(K_(2))(hArr)` `2SO_(2)(g) + O_(2) (g)`
What is the relation between `K_(1)` and `K_(2)`?
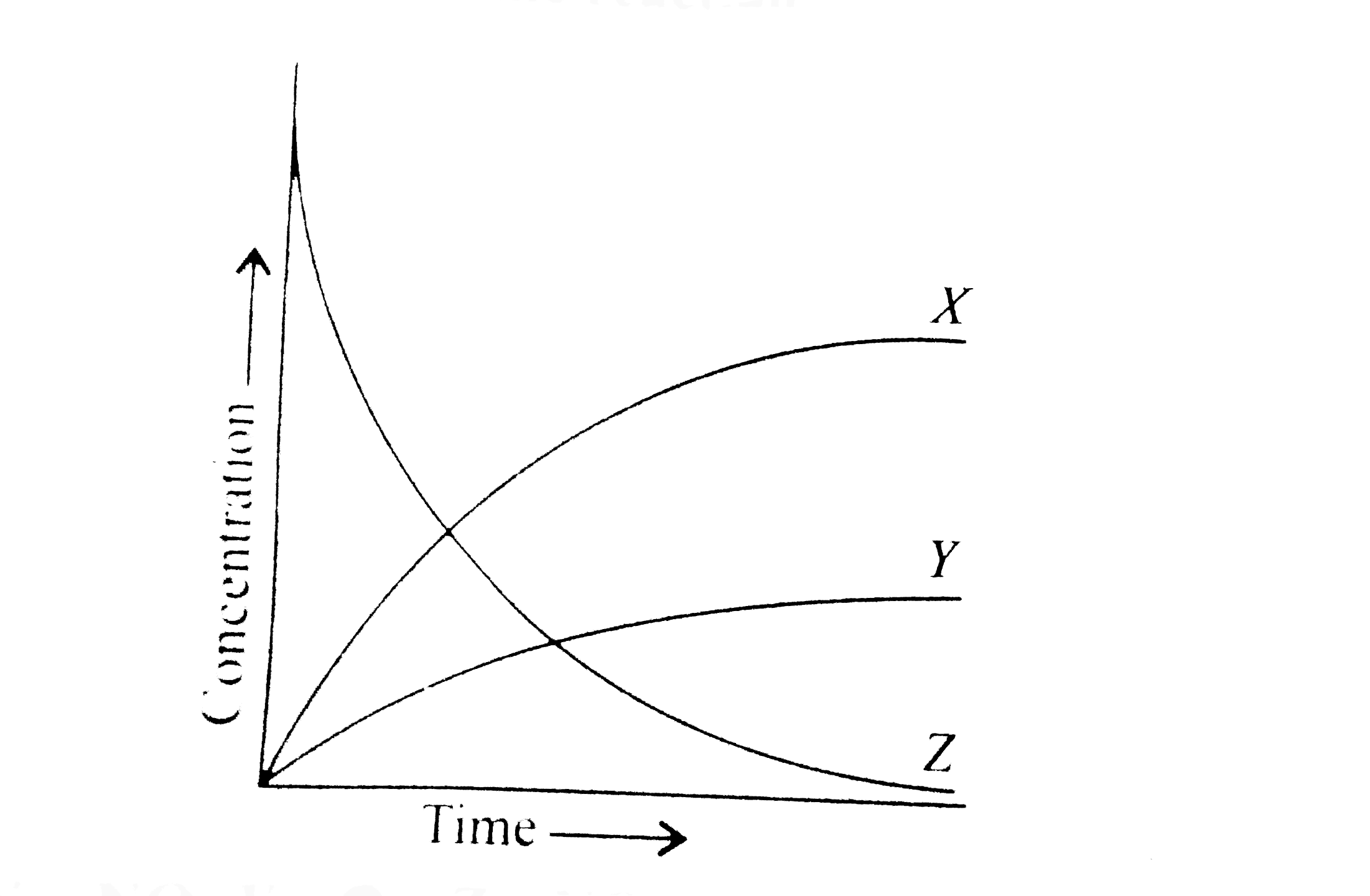
View SolutionConsider the following reaction:
`2NO_(2)(g) rarr 2NO(g)+ O_(2)(g)`
In the figure below, identify the curves `X,Y,` and `Z` associated with the three species in the reaction
View SolutionTwo equilibrium `ABhArrA^(+)+B^(-)` and `AB+B^(-)hArrAB_(2)^(-)` are simultaneously maintained in a solution with equilibrium constants `K_(1)` and `k_(2)`, respectively. Ratio of `[A^(+)]` to `[AB_(2)^(-)]` in the solution is
View SolutionAt `1400 K, K_( c) = 2.5 xx 10^(-3)` for the reaction
`CH_(4)(g)+2H_(2)S(g)hArrCS_(2)(g)+4H_(2)(g)`
A ` 10 L` reaction vessel at `1400 K` contains `2.0 mol` of `CH_(4)`, `4.0 mol` of `H_(2)S` ,`3.0 mol` of `CS_(2)`, `3.0 mol` of `H_(2)`. In which direction does the reaction proceed to reach equilibrium?
View SolutionFor the reaction
`PCl_(5)(g)hArrPCl_(3)(g)+Cl_(2)(g)`
Which of the following sketches may represent above equilibrium? Assume equilibrium can be achieved from either side and by taking any one or more components initially. Give `K_(c )` for the reaction `lt 2`?
View Solutiona. For which of the following reactions, `K_(p)` is equal to `K_(c)` ?
i. `H_(2)+I_(2)hArr2HI`
ii. `N_(2)+3H_(2)hArr2NH_(3)`
iii. `PCl_(5)hArrPCl_(3)+Cl_(2)`
b. For which of the following cases does the reaction go garthest to completion:
`K=1, K=10^(10), K=10^(-10)`?
View SolutionBoth matels Mg and Fe can reduce copper metal from a solution having copper ions `(Cu^(2+))`. According to the equilibria:
`Mg(s)+Cu^(2+)hArrMg^(2+)+Cu(s), K_(1)=6xx10^(90)`
`Fe(s)+Cu^(2+)hArrFe^(2+)+Cu(s), K_(2)=3xx10^(26)`
Which metal will remove cupric ion from the solution to a greater extent?
View SolutionThe equilibrium constant of the reaction
`H_(2)(g)+I_(2)(g)hArr2HI(g)`
at `426^(@)C` is `55.3`, what will be the value of equilibrium constant
a. if the reaction is reversed and
b. if the given reaction is represented as
`3H_(2)+3I_(2)hArr6HI`?
View SolutionWhat will be the effect on the equilibrium constant for the reaction `N_(2)+3H_(2)hArr2NH_(3),`
`DeltaH=-22.4` kcal, when
a. Pressure is increased
b. Concentration of `N_(2)` is increased and
c. Temperature is raised at equilibrium ?
View SolutionAt a certain temperature , the following reactions have the equilibrium constants as shown below:
`S(s)+O_(2)(g)hArrSO_(2)(g),K_(c)=5xx10^(52)`
`2S(s)+3O_(2)(g)hArr2SO_(3)(g),K_(c)=10^(29)`
what is the equilibrium constant `K_(c)`for the reaction at tahea same temperature?
`2SO_(2)(g)+O_(2)(g)hArr2SO_(3)(g)`
View SolutionFor a reversible reaction
`A+BhArrC`
`((dx)/(dt))=2.0xx10^(3) L mol^(-1) s^(-1) [A][B]-1.0xx10^(2) s^(-1) [C]` where `x` is the amount of 'A' dissociated. The value of equilibrium constant `(K_(eq))` is
View SolutionThe formation of amoonia from nitrogen and hydrogen gases can be written by the following two equations:
a. `1/2 N_(2)(g)+3/2H_(2)(g) lt lt NH_(3)(g)`
b. `1/3 N_(2)(g)+H_(2)(g) lt lt 2/3 NH_(3)(g)`
The two equations have equilibrium constants `K_(1)` and `K_(2)` respectively. The relationship between the equilibrium constant is
View SolutionThe following concentrations were obtained for the formation of `NH_(3)` from `N_(2)` and `H_(2)` at equilibrium at `500 K`. `[N_(2)] = 1.5 xx 10^(-2)M`. `[H_(2)] = 3.0 xx 10^(-2) M` and `[NH_(3)] = 1.2 xx 10^(-2) M`. Calculate equilibrium constant.
View SolutionAt equilibrium the concentrations of `N_(2) = 3.0 xx 10^(-3)M, O_(2) = 4.2 xx 10^(-3) M` and `NO = 2.8 xx 10^(-3) M` ina sealed vessel at `800 K`. What will be `K_(c)` for the reaction
`N_(2)(g) + O_(2)(h) hArr 2NO(g)`
View SolutionIn the reaction,
`H_(2)(g)+I_(2)(g)hArr2HI(g)`
The concentration of `H_(2), I_(2)`, and `HI` at equilibrium are `8.0, 3.0` and `28.0` mol per `L` respectively. Determine the equilibrium constant.
View Solution40% of a mixture of 0.2 mol of `N_(2)` and 0.6 mol of `H_(2)` react to give `NH_(3)` according to the equation : `N_(2)(g) + 3H_(2)(g) rarr 2NH_(3)(g)` at constant temperature and pressure. Then the ratio of the final volume to the initial volume of gases are :
View SolutionArrange the following in order of increasing tendency of the forward reactions to proceed towards completion at `298 K` and one atmospheric pressure :
a. `H_(2)O(g)hArrH_(2)O(l), K_(c)=782`
b. `F_(2)(g)hArr2F(g), K_(c)=4.9xx10^(-21)`
c. `C_("graphite")+O_(2)(g)hArrCO_(2)(g), K_(c)=1.3xx10^(69)`
d. `N_(2)O_(4)(g)hArr2NO_(2)(g), K_(c)=4.6xx10^(-3)`
e. `H_(2)(g)+C_(2)H_(4)(g)hArrC_(2)H_(6)(g), K_(c)=9.8xx10^(18)`
View SolutionThe equilibrium constant of the dissocition of various of an element A are given at constant temperature:
a.
Write the stability of these oxides in increasing order.
View SolutionAt
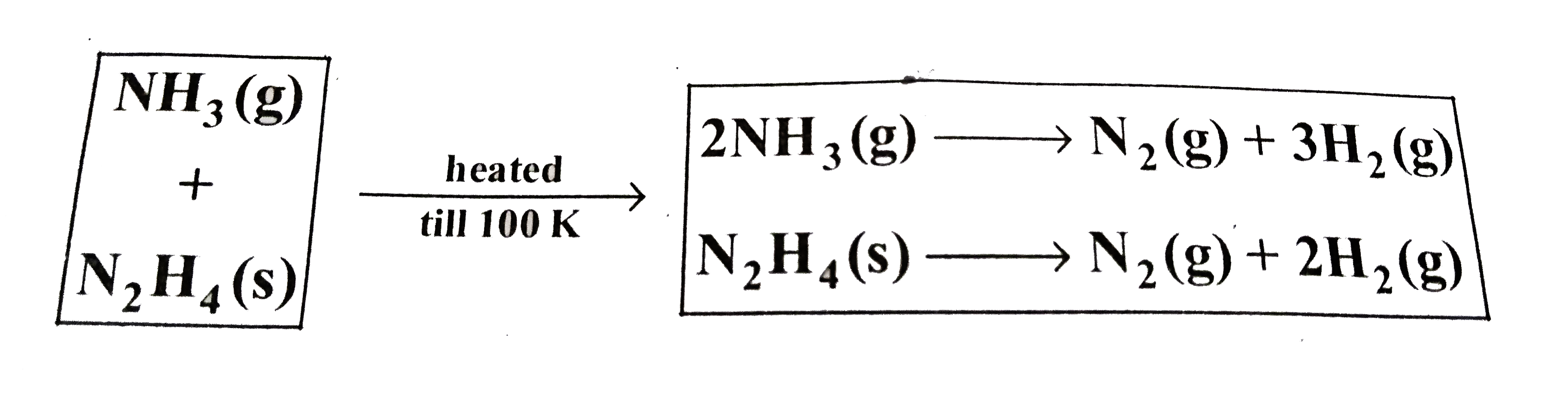
Assuming complete decomposition of `NH_(3)` and `N(2)H_(4)`
`P=0.3 atm, P=2.7 atm`
`T=300K, T=200K`
`VL, VL`
mole `%` of `NH_(3)` in original mixture is (assume both concentration same volume)
View SolutionWrite the expression for equilibrium constant for the following reactions. If the concentrations are expressed in `mol L^(-1)`, give the units in each case.
a.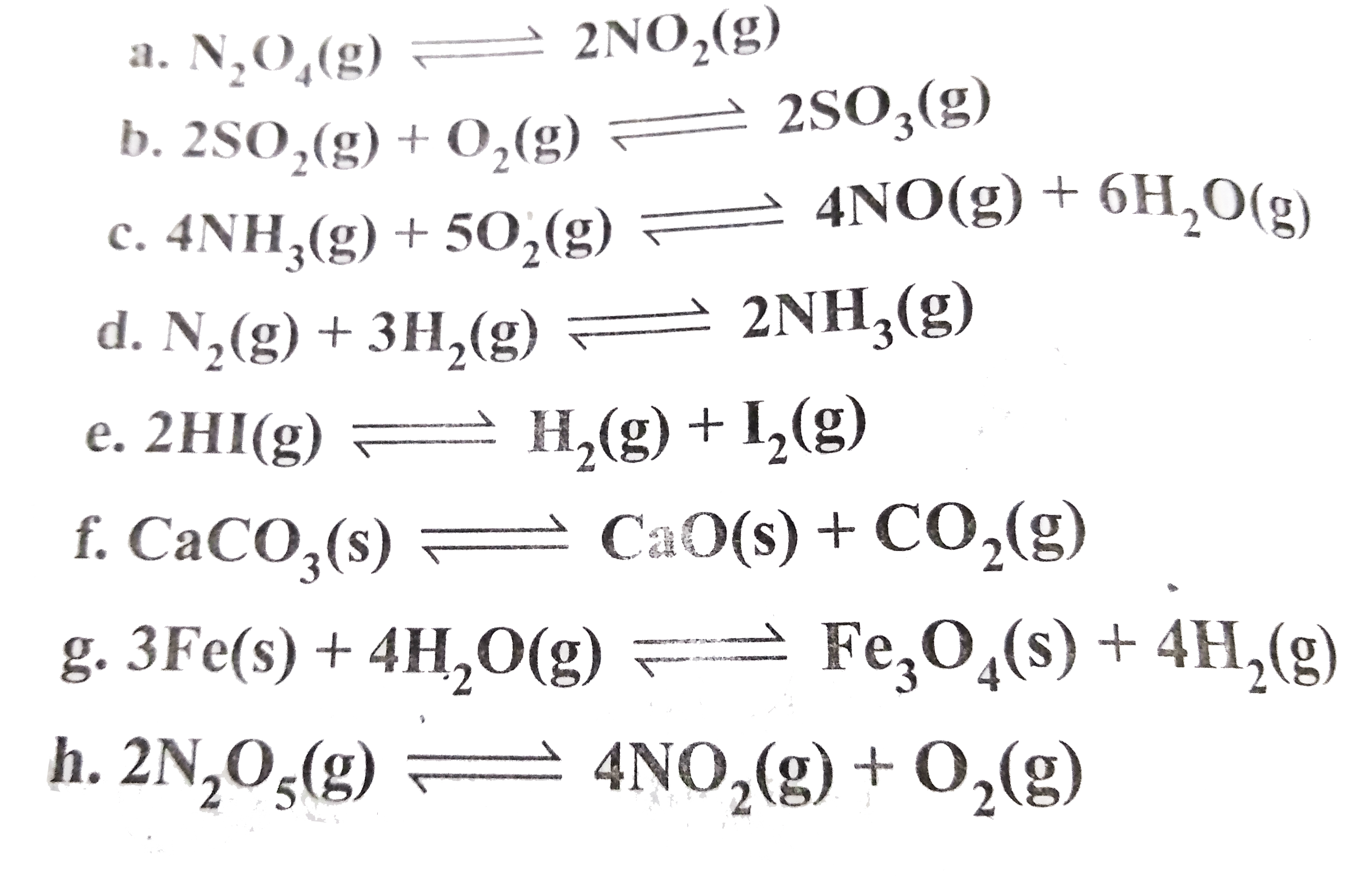
View SolutionAt a certain temperature, the equilibrium constant `(K_(c ))` is `16` for the reaction:
`SO_(2)(g)+NO_(2)(g)hArrSO_(3)(g)+NO(g)`
If we take one mole of each of the equilibrium concentration of `NO` and `NO_(2)`?
View SolutionA mixture of `SO_(3), SO_(2)` and `O_(2)` gases is maintained in a `10 L` flask at a temperature at which the equilibrium constant for the reaction is `100`:
`2SO_(2)(g)+O_(2)(g)hArr2SO_(3)(g)`
a. If the number of moles of `SO_(2)` and `SO_(3)` in the flask are equal. How many moles of `O_(2)` are present?
b. If the number of moles of `SO_(3)` in flask is twice the number of moles of `SO_(2)`, how many moles of oxygen are present?
View SolutionThe value of `K_(c )` for the reaction
`N_(2)(g)+3H_(2)(g)hArr2NH_(3)(g)`
is `0.50` at `400^(@)C`. Find the value of `K_(p)` at `400^(@)C` when concentrations are expressed in mol `L^(-1)` and pressure in atm.
View SolutionFor an ideal gas reaction
`2A+BhArrC+D`
the value of `K_(p)` will be:
View SolutionFor a reaction
`aA(g)hArrbB(g)`
at equilibrium, the heat of reaction at constant volume is `1500` cal more than at constant pressure. If the temperature is `27^(@)C` then
View SolutionGiven that `K_(c )` for equation (i) given below has a value of `256` at `1000 K`. Calculate the numerical values of `K_(c )` for other reactions `(ii), (iii),` and `(iv)`.
i.
View SolutionWhen `3.06 g` of solid `NH_(4)HS` is introduced into a two-litre evacuated flask at `27^(@)C, 30%` of the solid decomposes into gaseous ammonia and hydrogen sulphide. (i) Calculate `K_(c )` and `K_(p)` for the reaction at `27^(@)C`. (ii) What would happen to the equilibrium when more solid `NH_(4)HS` is introduced into the flask?
View SolutionAt `540 K, 0.10 mol` of `PCl_(5)` is heated in a `8L` flask. The pressure of equilibrium mixture is found to be `1.0 atm`. Calculate `K_(p)` and `K_(c )` for the reaction.
View SolutionProve that the pressure necessary to obtain `50%` dissociation of `PCl_(5)` at `250^(@)C` is numerically three times of `K_(p)`.
View SolutionFor the reaction
`CO(g)+2H_(2)(g)hArrCH_(3)OH(g)`
Hydrogen gas is introduced into a five-litre flask at `327^(@)C`, containing `0.2` mol of `CO(g)` and a catalyst, untill the pressure is `4.92 atm`. At this point, `0.1` mol of `CH_(3)OH(g)` is formed. Calculate the equilibrium constants `K_(p)` and `K_(c )`.
View SolutionWhen sulphur in the form of `S_(8)` is heated at `900 K`, the initial pressure of `1` atm falls by `10%` at equilibrium. This is because of conversion of some `S_(8)` to `S_(2)`. Find the value of equilibrium constant for this reaction.
View SolutionTwo solid `X` and `Y` dissociate into gaseous products at a certain temperature as followas:
`X(s)hArrA(g)+C(g)` , and `Y(s)hArrB(g)+C(g)`
At a given temperature, the pressure over excess solid `X` is `40 mm` and total pressure over solid `Y` is `80 mm`. Calculate
a. The value of `K_(p)` for two reactions.
b. The ratio of moles of A and B in the vapour state over a mixture of `X` and `Y`.
c. The total pressure of gases over a mixture of `X` and `Y`.
View SolutionFor a homogenous gaseous reaction
`X(g)+2Y)g)hArrZ(g)` ,
at `473 K`, the value of `K_(c )=0.35` concentration units. When `2` moles of `Y` are mixed with `1` mole of `X`, at what pressure `60%` of `X` is converted to `Z`?
View SolutionSolid `NH_(4)HS(s)` (ammonium hydrogen sulphate) dissociates to give `NH_(3)(g)` and `H_(2)S(g)` and is allowed to attain equilibrium at `100^(@)C`. If the value of `K_(p)` for its dissociation is found to be `0.34`, find the total pressure at equilibrium at `100^(@)C`. If the value of `K_(p)` for its dissociation is found to be `0.34`, find the total pressure at equilibrium and partial pressure of each component.
View SolutionAt `700 K`, the equilibrium constant `K_(p)` for the reaction
`2SO_(3)(g)hArr2SO_(2)(g)+O_(2)(g)`
is `1.80xx10^(-3) kPa`. What is the numerical value of `K_(c )` in moles per litre for this reaction at the same temperature?
View SolutionThe equilibrium of formation of phosgene is represented as :
`CO(g)+Cl_(2)(g)hArrCOCl_(2)(g)`
The reaction is carried out in a `500 mL` flask. At equilibrium, `0.3` mol of phosgene, `0.1 mol` of `CO`, and `0.1` mol of `Cl_(2)` are present.
The equilibrium constant of the reaction is
View SolutionWhich of the following relation(s) holds good for gaseous and reversible reactions?
View SolutionIf two gases `AB_(2)` and `B_(2)C` are mixed, following equilibria are readily established:
`AB_(2)(g)+B_(2)C(g)rarr AB_(3)(g)+BC(g)`,
`BC(g)+B_(2)C(g) rarr B_(3)C_(2)(g)`
If the reaction started only with `AB_(2)` with `B_(2)C`, then which of the following is necessarily true at equilibrium?
View SolutionThe degree of dissociation of `HI` at a particualr temperature is `0.8`. Calculate the volume of `2 M Na_(2)S_(2)O_(3)` solution required to neutralise the iodine present in an equilibrium mixture of a reaction when 2 mol each of `H_(2)` and `I_(2)` are heated in a closed vessel of `2 L` capacity and the equilibrium mixture is freezed.
View SolutionAt `1000K`, the pressure of iodine gas is found to be `0.1 atm` due to partial dissociation of `I_(2)(g)` into `I(g)`. Had there been no dissociation, the pressure would have been `0.07 atm`. Calculate the value of `K_(p)` for the reaction:
`I_(2)(g)hArr2I(g)` .
View SolutionCalculate the precentage dissociation of `H_(2)S(g)` if `0.1` mol of `H_(2)S` is kept in a `0.5 L` vessel at `1000 K`. The value of `K_(c )` for the reaction
`2H_(2)ShArr2H_(2)(g)+S_(2)(g)`
is `1.0xx10^(-7).`
View SolutionFor the reaction
`2HI(g)hArrH_(2)(g)+I_(2)(g)`
The degree of dissociation `(alpha)` of `HI(g)` is related to equilibrium constant `K_(p)` by the expression
a. `(1+2sqrt(K_(p)))/2`, b. `sqrt((1+2K_(p))/2)`
c. `sqrt((2K_(p))/(1+2K_(p)))`, d. `(2sqrt(K_(p)))/(1+2sqrt(K_(p)))`
View SolutionAt certain temperature compound `AB_(2)(g)` dissociates according to the reaction
`2AB_(2)(g) hArr2AB (g)+B_(2)(g)`
With degree of dissociation `alpha` Which is small compared with unity, the expression of `K_(p)` in terms of `alpha` and initial pressure P is :
View SolutionFor the dissociation reaction
`N_(2)O_(4)(g)hArr2NO_(2)(g),`
the equilibrium constant `K_(P)` is `0.120` atm at `298 K` and total pressure of system is `2` atm. Calculate the degree of dissociation of `N_(2)O_(4)`.
View SolutionA sample of air consisting of `N_(2)` and `O_(2)` was heated to `2500 K` until the equilibrium
`N_(2)(g)+O_(2)(g)hArr2NO(g)`
was established with an equlibrium constant, `K_(c )=2.1xx10^(-3)`. At equilibrium, the `"mole"%` of `NO` was `1.8`. Eatimate the initial composition of air in mole fraction of `N_(2)` and `O_(2)`.
View Solution`PCl_(5)` dissociates into `PCl_(3)` and `Cl_(2)`, thus
`PCl_(5)(g)hArrPCl_(3)(g)+Cl_(2)(g)`
If the total pressure of the system in equilibrium is `P` at a density `rho` and temperature `T`, show that the degree of dissociation `alpha=(PM)/(rhoRT)-1`, where `M` is the relative molar mass of `PCl_(5)`. If the vapour density of the gas mixture at equilibrium has the value of `62` when the temperature is `230^(@)C`, what is the value of `P//rho`?
View SolutionThe equilibrium constant `K_(p)` for the reaction
`N_(2)O_(4)(g)hArr2NO_(2)(g)`
at `497^(@)C` is found to be `636 mm Hg`. If the pressure of the gas mixture is `182 mm`, calculate the presentage dissociation of `N_(2)O_(4)`. At what pressure will it be dissociated?
View SolutionFor the reaction
`2HI(g)hArrH_(2)(g)+I_(2)(g)`
The degree of dissociation `(alpha)` of `HI(g)` is related to equilibrium constant `K_(p)` by the expression
a. `(1+2sqrt(K_(p)))/2`, b. `sqrt((1+2K_(p))/2)`
c. `sqrt((2K_(p))/(1+2K_(p)))`, d. `(2sqrt(K_(p)))/(1+2sqrt(K_(p)))`
View SolutionAt a given temperature and a total pressure of `1.0` atm for the homogenous gaseous reaction
`N_(2)_(4)hArr2NO_(2)(g),`
the partial pressure of `NO_(2)` is `0.5 atm`.
a. Find the value of `K_(p)`.
b.If volume of the vessel is decreased to half of its original volume, at constant temperature, what are the partial pressure of the components of the equilibrium mixture?
View SolutionIn the folowing reactions, the system will shift towards the forward reaction by adding inert gas at constant pressure?
`PCl_5->PCl_3+Cl_2`
View Solution`N_(2)O_(4)` dissociates as
`N_(2)O_(4)(g)hArr2NO_(2)(g)`
At `40^(@)C` and one atmosphere `%` decomposition of `N_(2)O_(4)` is `50.3%`. At what pressure and same temperature, the equilibrium mixture has the ratio of `N_(2)O_(4): NO_(2)` as `1:8`?
View SolutionAt `627^(@)C` and `1` atm `SO_(3)` is partially dissociated into `SO_(2)` and `O_(2)` by the reaction
`SO_(3)(g)hArrSO_(2)(g)+1//2O_(2)(g)`
The density of the equilibrium mixture is `0.925 g L^(-1)`. What is the degree of dissociation?
View SolutionDensity of equilibrium mixture of `N_(2)O_(4)` and `NO_(2)` at `1 atm` and `384 K` is `1.84 g dm^(-3)`. Calculate the equilibrium constant of the reaction.
`N_(2)O_(4)hArr2NO_(2)`
View SolutionFor the reaction
`NH_(3)(g)hArr(1)/(2)N_(2)(g)+(3)/(2)H_(2)(g)`
Show that the degree of dissociation of `NH_(3)` is given as
`alpha=[1+(3sqrt(3))/4p/K_(p)]^(-1//2)`
where p is equilibrium pressure. If `K_(p)` of the above reaction is `78.1 atm` at `400^(@)C`, calculate `K_(c )`.
View SolutionThe vapour density of `N_(2)O_(4)` at a certain temperature is `30`. Calculate the percentage dissociation of `N_(2)O_(4)` this temperature.
View Solution`3 g` mol of phosphorus is heated in a flask of `4 L` volume. At equilibrium, it dissociates to give `40%` of phosphorus trichloride and chlorine. Calculate the equilibrium constant.
View Solution`N_(2)O_(4)` is 25% dissociated at `37^(@)C` and one atmosphere pressure. Calculate (i) Kp and (ii) the percentage dissociation at 0.1 atm and `37^(@)C` .
View SolutionThe equation `alpha=(D-d)/((n-1)d)` is correctly matched for: (`alpha` is the degree of dissociation, D and d are the vapour densities before and after dissociation, respectively).
View SolutionThe vapour density of the equilibrium mixture of the reaction:
`SO_(2)Cl_(2)(g)hArrSO_(2)(g)+Cl_(2)(g)`
is `50`. The percent dissociation of `SO_(2)Cl_(2)` is
View SolutionConsider the following equilibrium in a closed container:
`N_(2)O_(4)(g)hArr2NO_(2)(g)`
At a fixed temperature, the volume of the reaction container is halved. For this change which of the following statements holds true regarding the equilibrium constant `(K_(p))` and the degree of dissociation `(alpha)`?
View SolutionAt certain temperature compound `AB_(2)(g)` dissociates according to the reaction
`2AB_(2)(g) hArr2AB (g)+B_(2)(g)`
With degree of dissociation `alpha` Which is small compared with unity, the expression of `K_(p)` in terms of `alpha` and initial pressure P is :
View SolutionThe following reaction occurs at `700 K`. Arrange them in the order of increasing tendency to proceed to completion.
I.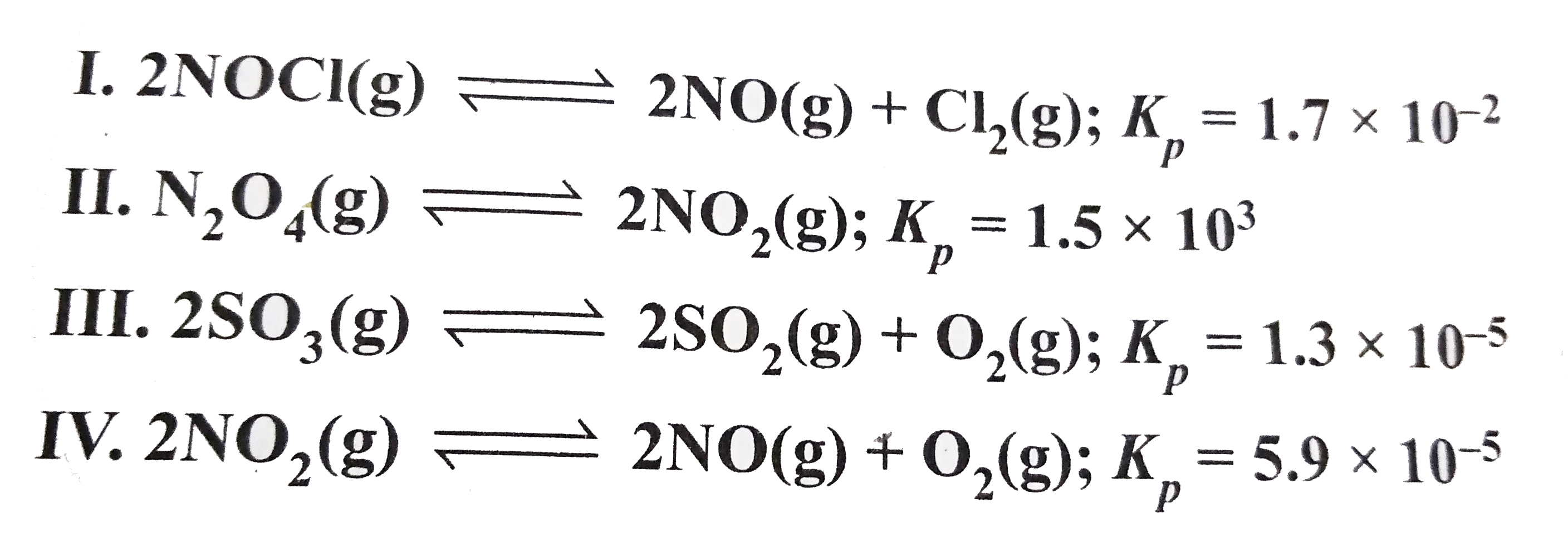
View SolutionAt `727^(@)C` and `1.2 atm` of total equilibrium pressure, `SO_(3)` is partially dissociated into `SO_(2)` and `O_(2)` as:
`SO_(3)(g)hArrSO_(2)(g)+(1)/(2)O_(2)(g)`
The density of equilibrium mixture is `0.9 g//L`. The degree of dissociation is:, `[Use R=0.08 atm L mol^(-1) K^(-1)]`
View Solution`K_(p)` for the reaction
`PCl_(5)(g)ghArrPCl_(3)(g)+Cl_(2)(g)`
at `250^(@)C` is `0.82`. Calculate the degree of dissociation at given temperature under a total pressure of `5 atm`. What will be the degree of dissociation if the equilibrium pressure is `10 atm`, at same temperature.
View SolutionIn reaction:
`CH_(3)COCH_(3)(g)hArrCH_(3)CH_(3)(g)+CO(g),`
if the initial pressure of `CH_(3)COCH_(3)(g)` is `150 mm` and at equilibrium the mole fraction of `CO(g)` is `1/3`, then the value `K_(P)` is
View SolutionWhen `PCl_(5)` is heated, it dissociates into `PCl_(3)` and `Cl_(2)`. The vapour density of the gas mixture at `200^(@)C` and at `250^(@)C` is `70` and `58`, respectively. Find the degree dissociation at two temperatures.
View Solution`0.25` mol of `CO` taken in a `1.5 L` flask is maintained at `500 K` along with a catalyst so that the following reaction can take place:
`CO(g)+H_(2)(g)hArrCH_(3)OH(g)` .
Hydrogen is introduced until the total pressure of system is `8.2 atm`, at equilibrium, and `0.1 mol` of methanol is formed. Calculate
a. `K_(p)` and `K_(c )`
b. The final pressure if the same amount of `CO` and `H_(2)` as before are used but no catalyst so that the reaction does take place.
View SolutionAmmonia under a pressure of `15 atm`, at `27^(@)C` is heated to `327^(@)C` in a vessel in the presence of catalyst. Under these conditions, `NH_(3)` partially decomposes to `H_(2)` and `N_(2)`. The vessel is such that the volume remains effectively constant, whereas the pressure increases to `50 atm`. Calculate the precentage of `NH_(3)` actually decomposed.
View SolutionSolid Ammonium carbamate dissociates as:
`NH_(2)COONH_(4)(s)hArr2NH_(3)(g)+CO_(2)(g).`
In a closed vessel, solid ammonium carbonate is in equilibrium with its dissociation products. At equilibrium, ammonia is added such that the partial pressure of `NH_(3)` at new equilibrium now equals the original total pressure. Calculate the ratio of total pressure at new equilibrium to that of original total pressure. Also find the partial pressure of ammonia gas added.
View SolutionThe degree of dissociation of `I_(2)` molecule of `1000^(@)C` and underatmosperic is 40% by volume .if the disscoiation is reduced to 20% at he same temp ., total equilibrium pressure on the gas is:
View Solution`I_(2)(aq)+I^(-)(aq)hArr(aq).` We started with 1 mole of `I_(2)` and 0.5 mole of `I_(-)` in one litre flask.After equilibrium is reached , excess of `AgNO_(3)` gave 0.25 mole of yellow precipitate. Equilibium constant is :
View Solution
Solved Example questions and complete solutions for chapter CHEMICAL EQUILIBRIUM of CENGAGE CHEMISTRY (ENGLISH) of Class 11
All Exercises from CENGAGE CHEMISTRY Class 11 CHEMISTRY CHEMICAL EQUILIBRIUM
- Archives (Fill In The Blanks)
- Archives (Multiple Correct)
- Archives (Single Correct)
- Archives (Subjective)
- Archives (True/False)
- Concept Applicationexercise 7.1
- Ex 7.2
- Exercises (Assertion-Reasoning)
- Exercises (Fill In The Blanks)
- Exercises (Integer)
- Exercises (Linked Comprehensive)
- Exercises (Multiple Correct)
- Exercises (Single Correct)
- Exercises (Subjective)
- Exercises (True/False)
- Solved Example
- Subjective type