Complete Solutions to Comprehension of chapter CALORIMETRY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CALORIMETRY |
| CENGAGE PHYSICS | Comprehension |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
A body cools in a surrounding of constant temperature `30^@C` Its heat capacity is `2 J//^(@)C`. Initial temeprature of cooling is valid. The body cools to `38^@C` in 10 min
In further 10 min it will cools from `38^@C` to _____
View SolutionA body cools in a surrounding of constant temperature `30^@C` Its heat capacity is `2 J//^@C`. Initial temeprature of cooling is valid. The body cools to `38^@C` in 10 min
The temperature of the body In `.^@C` denoted by `theta`. The veriation of `theta` versus time t is best denoted as
View SolutionA body cools in a surrounding of constant temperature `30^@C` Its heat capacity is `2 J//^(@)C`. Initial temeprature of cooling is valid. The body cools to `38^@C` in 10 min
When the body temperature has reached `38^@C`, it is heated again so that it reches `40^@C` in 10 min. The heat required from a heater by the body is
View SolutionThe inernal energy of a solid also increases when heat is transferred to it from its surroundings. A 5 kg solid bar is heated at atmospheric pressure. Its temperature increases from `20^@C` to `70^@C`. The linear expansion coefficient of solid bar is `1xx10^(-3)//^(@)C`. The density of solid bar is `50 kg//m^3`. The specific heat capacity of solid bar is `200 J//kg C^@`. The atmospheric pressure is `1xx10 N//m^2`.
The work done by the solid bar due to thermal expansion, under atmospheric pressure is
View SolutionThe inernal energy of a solid also increases when heat is transferred to it from its surroundings. A 5 kg solid bar is heated at atmospheric pressure. Its temperature increases from `20^@C` to `70^@C`. The linear expansion coefficient of solid bar is `1xx10^(-3)//^(@)C`. The density of solid bar is `50 kg//m^3`. The specific heat capacity of solid bar is `200 J//kgC^@`. The atmospheric pressure is `1xx10N//m^2`.
The heat transferred to the solid bar is
View SolutionThe inernal energy of a solid also increases when heat is transferred to it from its surroundings. A 5 kg solid bar is heated at atmospheric pressure. Its temperature increases from `20^@C` to `70^@C`. The linear expansion coefficient of solid bar is `1xx10^(-3)//^(@)C`. The density of solid bar is `50 Kg//m^3`. The specific heat capacity of solid bar is `200 J//kg C^@`. The atmospheric pressure is `1xx10 N//m^2`.
The increase in the internal energy of the sold bar is
View SolutionA wire of length 1 m and radius `10^-3`m is carrying a heavy current and is assumed to radiate as a black body. At equilibrium, its temperature is 900 K while that of surrounding is 300 K. The resistivity of the material of the wire at 300 K is `pi^@xx10^-8` ohm m and its temperature coefficient of resistance is `7.8xx10^(-3)//C` (stefan's constant`sigma=5.68xx10^-8W//m^(2) K^(4)`).
Q. The resistivity of wire at 900 K is nearly
View SolutionA wire of length 1 m and radius `10^-3`m is carrying a heavy current and is assumed to radiate as a black body. At equilibrium, its temperature is 900 K while that of surrounding is 300 K. The resistivity of the material of the wire at 300 K is `pi^@xx10^-8` ohm m and its temperature coefficient of resistance is `7.8xx10^(-3)//C` (stefan's constant`sigma=5.68xx10^-8W//m^(2) K^(2)`.
Heat radiated per second by the wire is nearly
View SolutionA wire of length 1 m and radius `10^-3`m is carrying a heavy current and is assumed to radiate as a black body. At equilibrium, its temperature is 900 K while that of surrounding is 300 K. The resistivity of the material of the wire at 300 K is `pi^@xx10^-8` ohm m and its temperature coefficient of resistance is `7.8xx10^(-3)//C` (stefan's constant`sigma=5.68xx10^-8W//m^(2) K^(2)`.
The current in the wire is nearly
View SolutionAssume that the thermal conductivity of copper is twice that of aluminium and four times that of brass. Three metal rods made of copper, aluminium and brass are each 15 cm long and 2 cm in diameter. These rods are placed end to end, with aluminium between the other two. The free ends of the copper and brass rods are maintained at `100^@C` and `0^@C` respectively. The system is allowed to reach the steady state condition. Assume there is no loss of heat anywhere.
When steady state condition is reached everywhere, which of the following statement is true?
View SolutionAssume that the thermal conductivity of copper is twice that of aluminium and four times that of brass. Three metal rods made of copper, aluminium and brass are each 15 cm long and 2 cm in diameter. These rods are placed end to end, with aluminium between the other two. The free ends of the copper and brass rods are maintained at `100^@C` and `0^@C` respectively. The system is allowed to reach the steady state condition. Assume there is no loss of heat anywhere.
Under steady state condition the equilibrium temperature of the copper aluminium junction will be
View SolutionAssume that the thermal conductivity of copper is twice that of aluminium and four times that of brass. Three metal rods made of copper, aluminium and brass are each 15 cm long and 2 cm in diameter. These rods are placed end to end, with aluminium between the other two. The free ends of the copper and brass rods are maintained at `100^@C` and `0^@C` respectively. The system is allowed to reach the steady state condition. Assume there is no loss of heat anywhere.
Under steady state condition the equilibrium temperature of the copper aluminium junction will be
View SolutionA thin copper rod of uniform cross section A square metres and of length L metres has a spherical metal sphere of radius r metre at tis one end symmetrically attached to the copper rod. The thermal conductivity of copper is K and the emissivity of the spherical surface of the sphere is `epsi`.The free end of the copper rod is maintained at the temperature T kelving by supplying thermal energy from a P watt source. Steady state conditions are allowed ot be established while the rod is properly insulated aginst heat loss from its lateral surface. Surroundings are at `0^@C` Stefan's constant`=sigma W//m^(2) K^(4)`.
After the steady state conditions are reached,the temperature of the spherical end of the rod, `T_S` is
View SolutionA thin copper rod of uniform cross section A square metres and of length L metres has a spherical metal sphere of radius r metre at tis one end symmetrically attached to the copper rod. The thermal conductivity of copper is K and the emissivity of the spherical surface of the sphere is `epsi`.The free end of the copper rod is maintained at the temperature T kelving by supplying thermal energy from a P watt source. Steady state conditions are allowed ot be established while the rod is properly insulated aginst heat loss from its lateral surface. Surroundings are at `0^@C` Stefan's constant`=sigmaW//m^(2) K^(4)`.
The net power that will be radiated out, `P_S` from the sphere after steady state condition are reached is
View SolutionA thin copper rod of uniform cross section A square metres and of length L metres has a spherical metal sphere of radius r metre at tis one end symmetrically attached to the copper rod. The thermal conductivity of copper is K and the emissivity of the spherical surface of the sphere is `epsi`.The free end of the copper rod is maintained at the temperature T kelving by supplying thermal energy from a P watt source. Steady state conditions are allowed ot be established while the rod is properly insulated aginst heat loss from its lateral surface. Surroundings are at `0^@C` Stefan's constant`=sigma W//m^(2)K^(4)`.
If the metal sphere attached at the end of the copper rod is made of brass, whose thermal conductivity is `K_b lt K`, then which of the following statements is true?
View SolutionAn immersion heater, in an insulated vessel of negligible heat capacity brings 10 g of water to the boiling point from `16^@C` in 7 min. Then
Q. Power of heat is nearly
View SolutionAn immersion heater, in an insulated vessel of negligible heat capacity brings 10 g of water to the boiling point from `16^@C` in 7 min. Then
Q. The water is replaced by 200 g of alcohol, which is heated from `16^@C` to the boiling point of `78^@C` in 6 min 12 s whereas 30 g are vapourized in 5 min 6 s. The specific heat of alcohol is
View SolutionAn immersion heater, in an insulated vessel of negligible heat capacity brings 10 g of water to the boiling point from `16^@C` in 7 min. Then The heat of vapourization of alcohol is
View SolutionA body of area `0.8xx10^-2m^2` and mass `5xx10^(-4)kg` directly faces the sun on a clear day. The body has an emissivity of 0.8 and specific heat of `0.8 cal//kg` K. The surroundings are at `27^@C`. (solar constant `=1.4 kW//m^(2)`). Q. The rate of rise of the body's temperature is nearly
View SolutionA body of area `0.8xx10^(-2) m^(2)` and mass `5xx10^(-4) kg` directly faces the sun on a clear day. The body has an emissivity of 0.8 and specific heat of `0.8 ca//kg` K. The surroundings are at `27^@C`. (solar constant`=1.4 kW//m^(2)`).
The maximum attainable temperature of the body is
View SolutionA body of area `0.8xx10^-2m^2` and mass `5xx10^-4kg` directly faces the sun on a clear day. The body has an emissivity of 0.8 and specific heat of `0.8 cal//kg` K. The surroundings are at `27^@C`. (solar constant`=1.4 kW//m^(2)`).
The temperature that the body would reach if it lost all its heat by radiation is
View SolutionA copper collar is to fit tightly about a steel shaft that has a diameter of 6 cm at `20^@C`. The inside diameter of the copper collar at the temperature is `5.98cm`
Q. To what temperature must the copper collar be raised to that it will just slip on the steel shaft, assuming the steel shaft remains at `20^@C` ? `(alpha_("copper")=17xx10^(-6)//K`)
View SolutionA copper collar is to fit tightly about a steel shaft that has a diameter of 6 cm at `20^@C`. The inside diameter of the copper collar at the temperature is `5.98cm`
Q. The tensile stress in the copper collar when its temperature returns to `20^@C` is `(T=11xx10^10N//m^(2))`
View SolutionA copper collar is to fit tightly about a steel shaft that has a diameter of 6 cm at `20^@C`. The inside diameter of the copper collar at the temperature is `5.98cm`
If the breaking stress of copper is `230 N//m^2`, at what temperature will the copper collar break as it cools?
View Solution
Two insulated metal bars each of length 5 cm and rectangular cross section with sides 2 cm and 3 cm are wedged between two walls, one held at `100^@C` and the other at `0^@C`. The bars are made of lead and silver. `K_(pb)=350 W//mK,K_(Ag)=425W//mK`.
Thermal corrent through lead bar is
View Solution
Two insulated metal bars each of length 5 cm and rectangular cross section with sides 2 cm and 3 cm are wedged between two walls, one held at `100^@C` and the other at `0^@C`. The bars are made of lead and silver. `K_(pb)=350 W//mK,K_(Ag)=425 W//mK`.
Total thermal current through the two bar system is
View Solution
Two insulated metal bars each of length 5 cm and rectangular cross section with sides 2 cm and 3 cm are wedged between two walls, one held at `100^@C` and the other at `0^@C`. The bars are made of lead and silver. `K_(pb)=350 W//mK,K_(Ag)=425 W//mK`.
Equevalent thermal resistence of the two bar system is
View Solution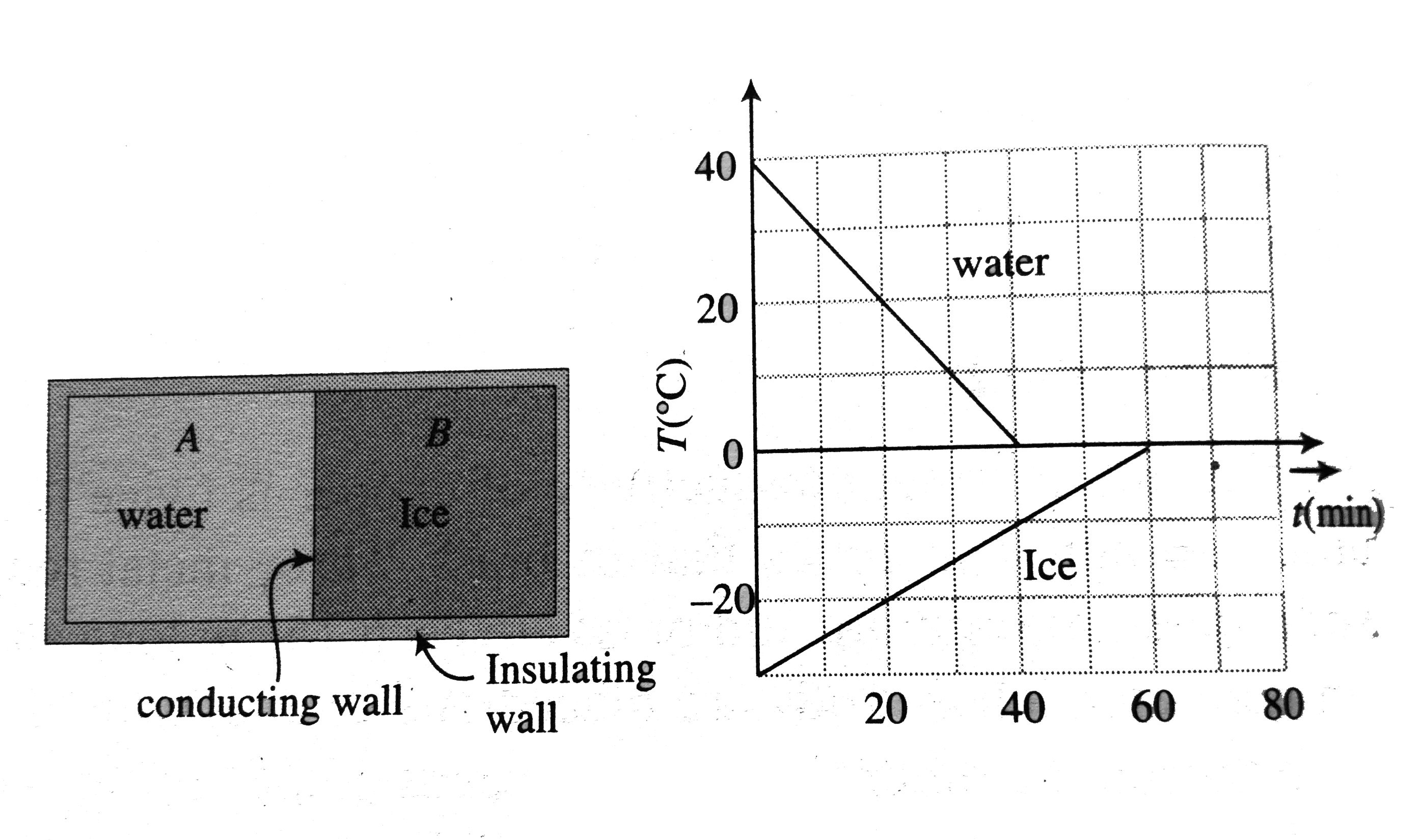
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice `=2100 J//kg-K`, specific heat of water `=4200 J//kg-K`, and latent heat of fusion of ice `=3.3xx10^5 J//kg`.
View Solution
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice `=2100 J//kg-K`, specific heat of water `=4200 J//kg-K`, and latent heat of fusion of ice `=3.3xx10^5 J//kg`.
Initial mass of the ice in the container equal to
View Solution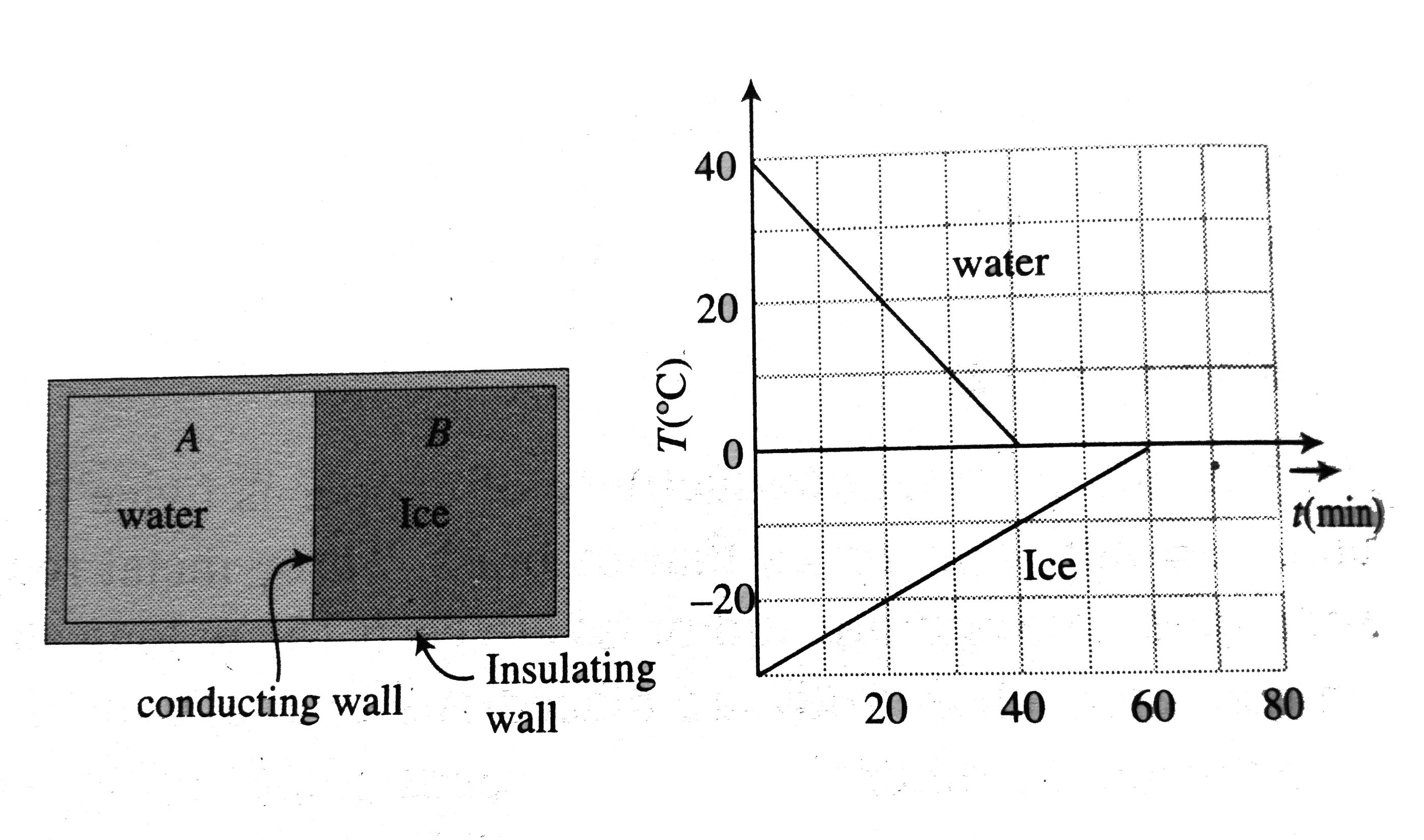
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice `=2100 J//kg-K`, specific heat of water `=4200 J//kg-K`, and latent heat of fusion of ice `=3.3xx10^5 J//kg`.
The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal to
View Solution
Comprehension questions and complete solutions for chapter CALORIMETRY of CENGAGE PHYSICS (HINGLISH) of Class 11