Complete Solutions to Subjective of chapter CALORIMETRY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CALORIMETRY |
| CENGAGE PHYSICS | Subjective |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
A lead ball at `25^@`C is dropped from a height of 2 km. It is heated due to air resistance and it is assumed that all of its kinetic energy is used in increasing the temperature of ball. Find the final temperature of the ball.
View SolutionThe temperatures of equal masses of three different liquids A, B and C are `15^@C`, `-20^@C` and `30^@C`, respectively. When A and B are mixed their equilibrium temperature is `180^@C`. When B and C are mixed, it is `22^@C` .What will be the equilibrium temperature when liquids A and C are mixed
View SolutionA copper cube of mass `200g` slides down an a rough inclined plane of inclination `37^(@)` at a constant speed. Assume that any loss in mechanical energy goes into the copper block as thermal energy .Find the increase in the temperature of the block as it slides down through `60cm`. Specific heat capacity of copper `= 420J kg^(-1) K^(-1)`
View SolutionFind the result of mixing 0.5 kg ince at `0^@C` with 2 kg water at `30^@C`. Given that latent heat of ice is `L=3.36xx10^5 J//kg` and specific heat of water is `4200 J//kg//K`.
View Solution1 g ice at `0^@C` is placed in a calorimeter having 1 g water at `40^@C`. Find equilibrium temperature and final contents. Assuming heat capacity of calorimeter is negligible small.
View Solution1 g ice at `-40^@C`. Is placed in a container having 1 g water at `1^@C`. Find equilibrium temperature. Assume heat capacity of container is negligibly small.
View Solution1 g of ice at `0^@C` is mixed with 1 g of steam at `100^@C`. After thermal equilibrium is achieved, the temperature of the mixture is
View SolutionA clock with a metallic pendulum gains 5 s each day at a temperature of `15^@C` and loses 10 s each day at a temperature of `30^@C`. Find the coefficient of thermal expansion of the pendulum metal.
View SolutionA rod AB of length l is pivoted at an end A and freely rotated in a horizontal plane at an angular speed `omega` about a vertical axis passing through A. If coefficient of linear expansion of material of rod is `alpha`, find the percentage change in its angular velocity if temperature of system is incresed by `DeltaT`
View Solution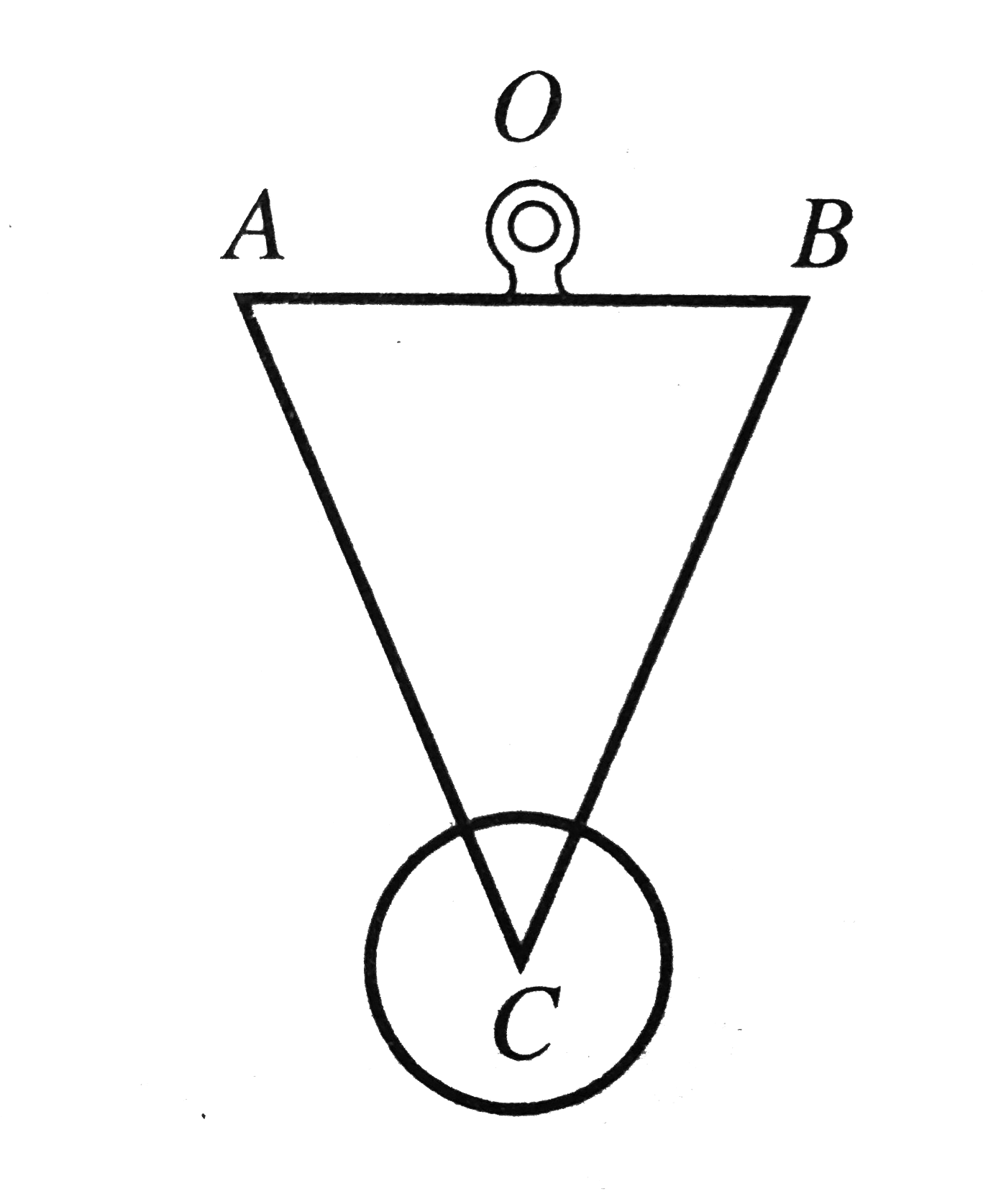
A compensated pendulum shown if Fig. is in the from of an isosceles Delta of base length `l_1=5`cm and coefficent of linar expansion `alpha_1=18xx10^-6` and side length `l_2` and coefficient of linear expansion `alpha_2=12xx10^-6`. find `l_2` so the the distance of centre of mass of the bob from suspension centre O may remain the same at all the temperature.
View SolutionA aluminium can of cylindrical shape contains `500cm^3` of water. The area of the inner cross section of the can is `125cm^2`. All measurements refer ti `10^@C`. Find the rise in the water level if the temperature increases to`80^@C`. The coefficient of linear expansion of aluminium `=23 xx 10^(-6 @ )C(-1)` respectively.
View Solution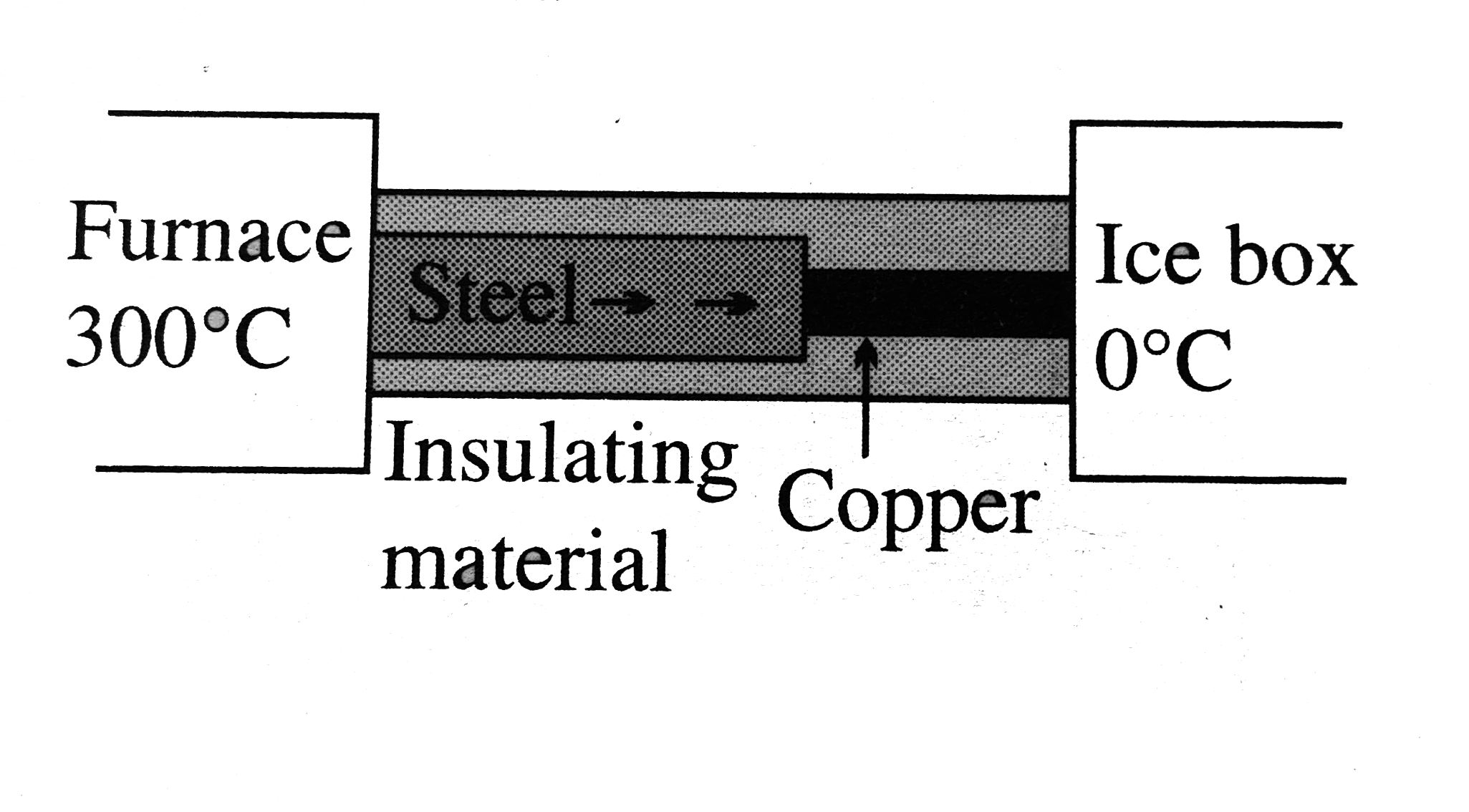
What is the temperature of the steel-copper junction in the steady state of the system shown if Fig? Length of the steel rod `=25cm`, length of the copper rod`=50cm`, temperature of the furnace`=300^@C`, temperature of the other end `=0^@C`. The area of cross section of the steel rod is twice that of the copper rod. (Thermal conductivity of steel `=50J//sm` and of copper `=400Js//mK`).
View SolutionWe would like to increase the length of a 15 cm long copper rod of cross section `4mm^2` by 1 mm. The energy absorbedd by the rod if it is heated is `E_1`. The energy absorbed by the rod if it is stretched slowly is `E_2`. Then find `E_1//E_2`. [Variaous parameters of copper are density `=9xx10^3 Kg//m^(3)`, thermal coefficient of linear expansion `=16xx10^-6//K`, Young's modulus `=135xx190Pa`, specific heat `= 400 J//kg-K`]
View SolutionA uniform rod of thermal conductivity of `65J//m-s-^(@)C` is surrounded by an insulator on its sides. One of its ends is put in a furnace, while the other end is kept exposed. If the temperature gradient of the rod is `-75^@C//m`, find the emissive power of the exposed end.
View SolutionA cylinderical brass boiler of radius 15 cm and thickness 1.0 cm is filled with water and placed on an elerctric heater. If the If the water boils at the rate of `200 g//s`, estimate the temperature of the heater filament. Thermal conductivity of `brass=109 J//s//m^@C` and heat of vapourization of water `=2.256xx10^3 J//g`.
View SolutionThe lower surface of a slab of stone of face-area `3600cm^(2)` and thickness `10cm` is exposed to steam at `100^(@)C` . A block of ice at `0^(@)C` rests on the upper surface of the slab. `4.8g` of ice melts in one hour. Calculate the thermal conductivity of the stone. Latent heat of fusion of ice `=3.36xx10^(5) J kg^(-1)`
View SolutionA cube of mass 1 kg and volume `125cm^2` is placed in an evacuated chamber at `27^@C`. Initially temperature of block is `227^@C`. Assume block behaves like a block body, find the rate of cooling of block if specific heat of the material of block is `400 J//kg-K`.
View SolutionA solid metallic sphere of diameter 20 cm and mass 10 kg is heated to a temperature of `327^@C` and suspended in a box in which a constant temperature of `27^@C` is maintained. Find the rate at which the temperature of the Sphere will fall with time. Stefan's constant`=5.67xx10^-8W//m^(2)//K^(4)` and specific heat of metal `=420J//kg//^(@)C`.
View SolutionFigure shows water in a container having `2.0mm` thick walls made of a material of thermal conductivity `0.50Wm^(-1).^(@)C^(-1)` . The container is kept in a melting-ice bath at `0^(@)C` . The total surface area in contact with water is `0.05m^(2)` . A wheel is clamped inside the water and is coupled to a block of mass M as shown in the figure. As the block goes down, the wheel rotates. It is found that after some time a steady state is reached in which the block goes down with a constant speed of `10cm^(-1)` and the temperature of the water remains constant at `1.0^(@)C` .Find the mass `M` of the block. Assume that the heat flow out of the water only through the walls in contact. Take `g=10ms^(-2)` .

View SolutionLet us assume that sun radiates like a black body with surface temperature at `T_0=6000K` and earth absorbs radiation coming from sun only. If both earth and sun are considered perfect spheres with distance between centre of earth and centre of sun to be 200 times the radius of sun, find the temperature (in Kelvin) of surface of earth in steady state (assume radiation incident on earth to be almost parallel).
View SolutionWater flows at the rate of `0.1500 kg//min` through a tube and is heated by a heater dissipating `25.2W`. The inflow and outflow water temperatures are `15.2^@C` and `17.4^@C`, respectively. When the rate of flow is increased to `0.2318 kg//min` and the rate of heating to `37.8W`, the inflow and outflow temperature are unaltered. Find
i. the specific heat capacity of water
ii. the rate of loss of heat from the tube.
View SolutionA piece of metal weighs 46 g in air and 30 g in lipuid of density `1.24 xx 10^3 kg m^(-3)` kept at `27^0C`. When the temperature of the liquid is raised to `42^0C` the metal piece weights 30.5 g . The density of the liqued at `42^0 C` is `1.20 xx 10^3 kg m^(-3)`. Calculate the coefficient of linear expandsion of the metal.
View SolutionTwo steel rods and an aluminium rod of equal length `l_0` and equal cross- section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at `0^@ C`
 . Find the length of the system when the temperature is raised to `theta`. Coefficient of linear expansion of aluminium and steel are `alpha_(a)` and `alpha_(s)` respectively. Young's modulus of aluminium is `Y_(a)` and of steel is `Y_(s)`.
. Find the length of the system when the temperature is raised to `theta`. Coefficient of linear expansion of aluminium and steel are `alpha_(a)` and `alpha_(s)` respectively. Young's modulus of aluminium is `Y_(a)` and of steel is `Y_(s)`.
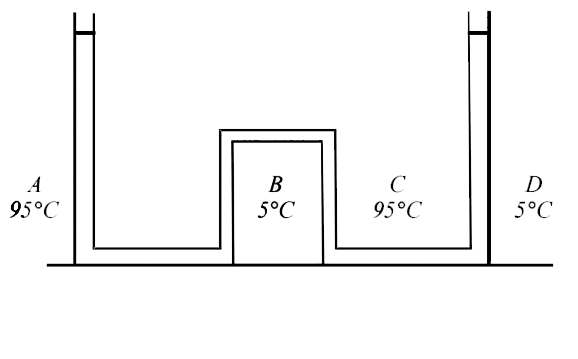
View SolutionThe apparatus shown in the figure consists of four glass columns connected by horizontal section. The height of two central column B and C are 49 cm each. The two outer columns A and D are open to the temperature. A and C are maintained at a temperature of `95^@C` while the columns B and D are maintained at `5^@C`. The height of the liquid in A and D measured from the base the are 52.8 cm and 51cm respectively. Determine the coefficient of thermal expansion of the liquid
View SolutionA cylindrical rod of length `50cm` and cross sectional area `1cm^(2)` is fitted between a large ice chamber at `0^(@)C` and an evacuated chamber maintained at `27^(@)C` as shown in figure. Only small portions of the rod are inside the chamber and the rest is thermally insulated from the surrounding. The cross section going into the evacuated chamber is blackened so that it completely absorbs any radiation falling on it. The temperature of the blackened end is `17^(@)C` when steady state is reached. Stefan constant `sigma=6xx10^(-s)Wm^(-2)K^(-4)` . Find the thermal conductivity of the material of the rod.

View Solution
Subjective questions and complete solutions for chapter CALORIMETRY of CENGAGE PHYSICS (HINGLISH) of Class 11