Complete Solutions to Exercise 1.3 of chapter CALORIMETRY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CALORIMETRY |
| CENGAGE PHYSICS | Exercise 1.3 |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
Explain why the surface of a lake freezes first.
View SolutionIn newton's law of cooling in the form
`(dDeltatheta)/(dt)=-kDeltatheta`
What factors does the constant k depend upon? What are the dimensions of k?
View SolutionA thermocole cubical icebox of side 30 cm has a thickness of 5.0 cm if 4.0 kg of ice are put ini the box, estimate the amount of ice remaining after 6 h. The outside temperature is `45^@C` and coefficient of thermal conductivity of thermocole`=0.01 J//kg`.
View SolutionA brass boiler has a base area of `0.15m^2` and thickness 1.0 cm it boils water at the rate of `6.0 kg//min`, When placed on a gas. Estimate the temperature of the part of the flame in contact with the boiler. Thermal conductivity of brass`=109 J//s-.^@C` ) and heat of vapourization of water `=2256 J//g`.
View SolutionAn electric heater is placed inside a room of total wall area `137 m^2` to maintain the temperature inside at `20^@C`. The outside temperature is `-10^@C`. The walls are made of three composite materials. The inner most layer is made of wood of thickness 2.5 cm the middle layer is of cement of thickness 1 cm and the exterior layer is of brick of thickness 2.5 cm. Find the power of electric heater assuming that there is no heat losses through the floor and ceiling. The thermal conductivities of wood, cement and brick are `0.125 W//m.^@C, 1.5W//m.^@C and 1.0 W//m.^@C` respectively.
View SolutionAn indirectly heated filament is radiating maximum energy of wavelength `2.16xx10^-5cm`. Find the net amount of heat energy lost per second per unit area, the temperature of the surrounding air is `13^@C`. Given `b=0.288cm-K.sigma=5.77xx10^-5erg//s-cm^(2)-K^(4)`).
View SolutionA uniform copper bar 100 cm long is insulated on side, and has its ends exposed to ice and steam respectively. If there is a layer of water 0.1 mm thick at each end, calculate the temperature gradient in the bar. `K_(Cu)=1.04` and `K_(water)=0.0014` in CGS units.
View Solution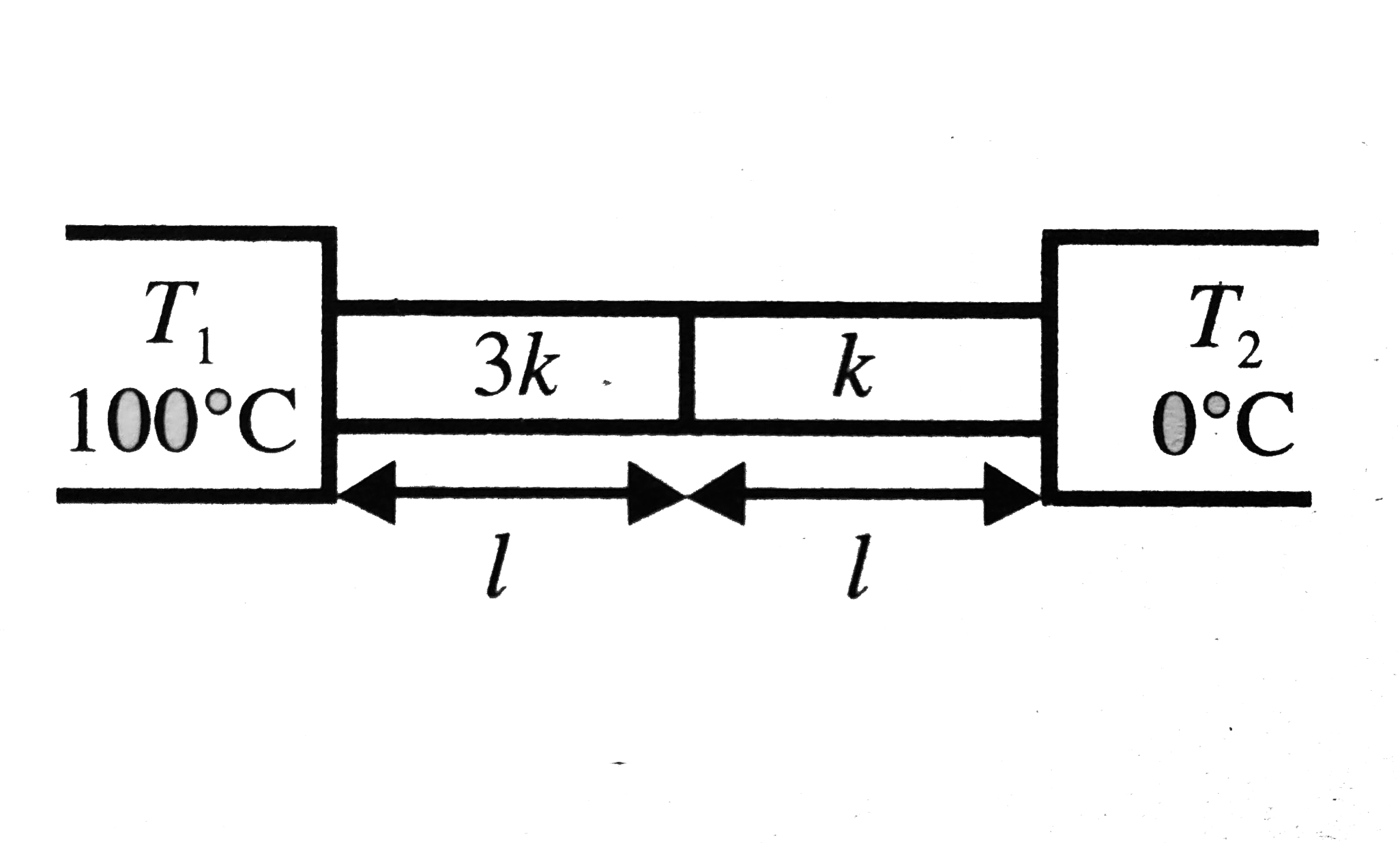
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of `100^@C` is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View Solution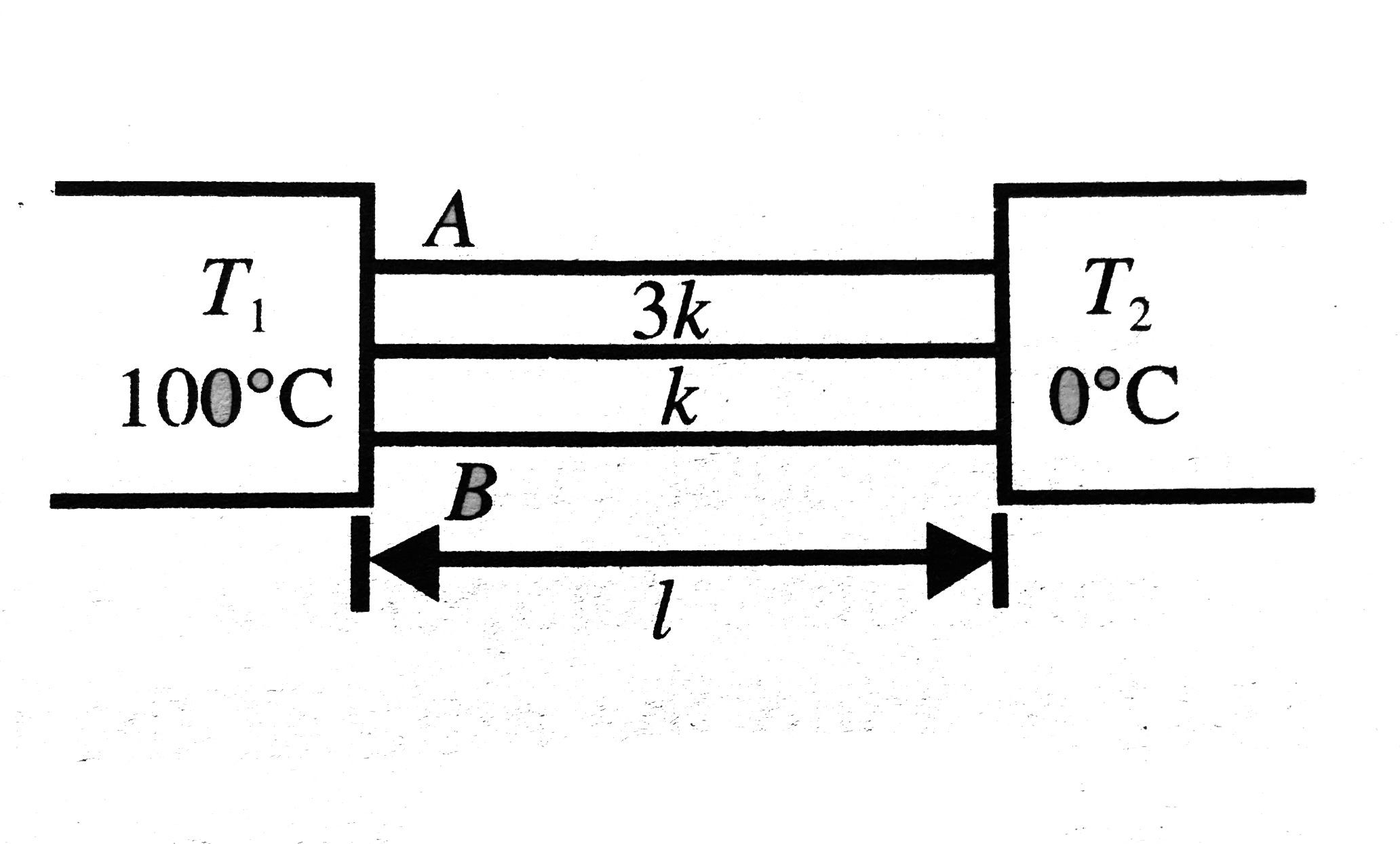
Two conductors A and B given in previous problem are connected in parallel as shown in Fig.
i. Determine the equivalent thermal resistance.
ii. Determine the heat current in each rod.
View SolutionA sphere, a cube and a thin circular pate are heated to the same temperature. If they are made of same material and have equal masses, determine which of these three object cools the fastest and which one cools the slowest?
View SolutionOne end of a brass rod of length 2.0 m and cross section `1cm^2` is kept in stream at `100^@C` and the other end in ice at `0^@C`. The lateral suface of the rod is covered by heat insulator. Determine the amount of ice melting per minute. Thermal conductivity of brass is `110 W//m-K` and specific latent heat of fusion of ice is `80 cal//g`.
View Solution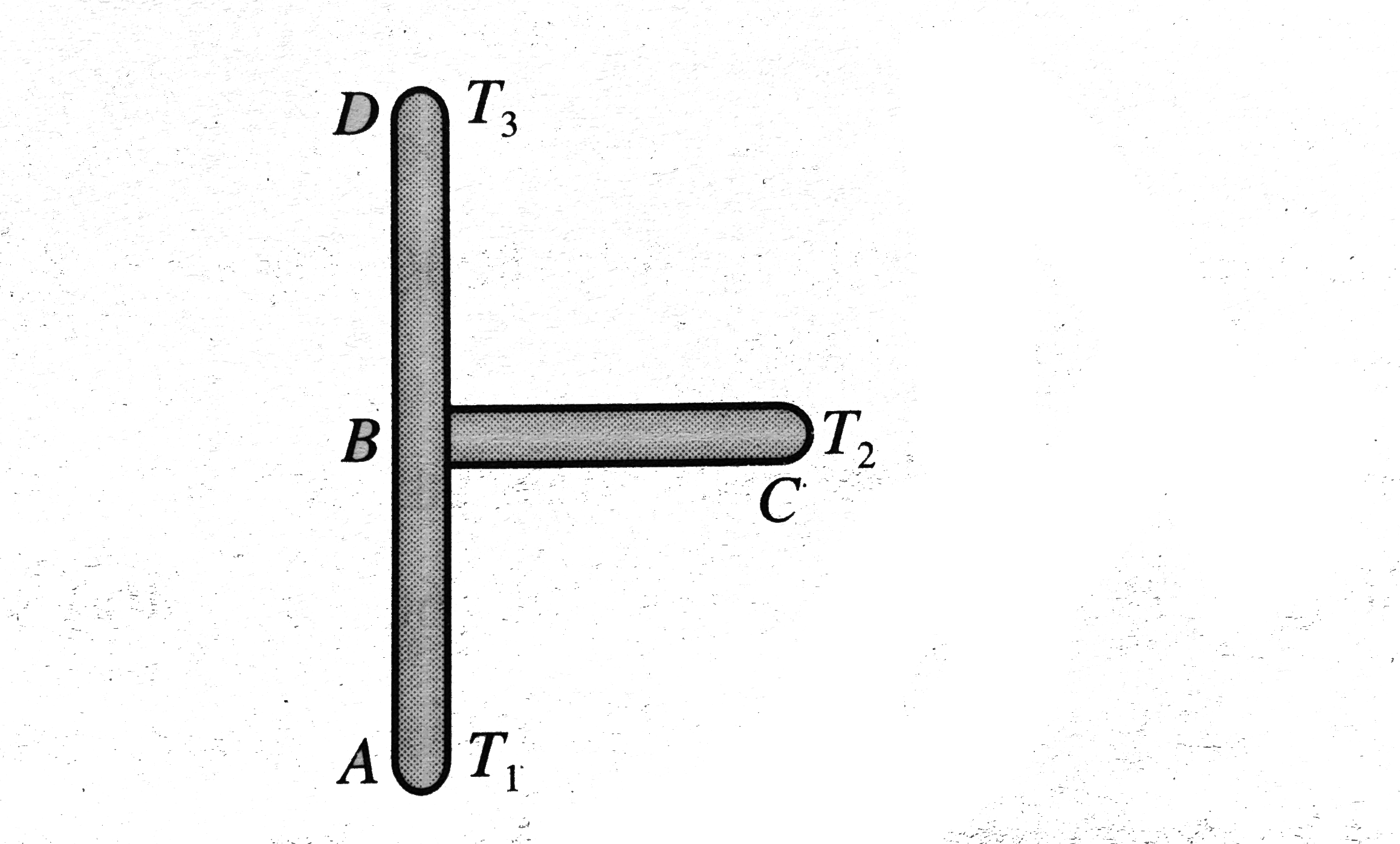
Three rods AB, BC and BD having thermal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in Fig. The ends A, C and D are at temperature `T_1`,`T_2` and `T_3` respectively Find the temperature of the junction B. Assume steady state.
View SolutionThermal conductivity of inner core of radius r is K and of the outer one of radius `2r` is 2K. Find equivalent value of thermal conductivity between its two ends.
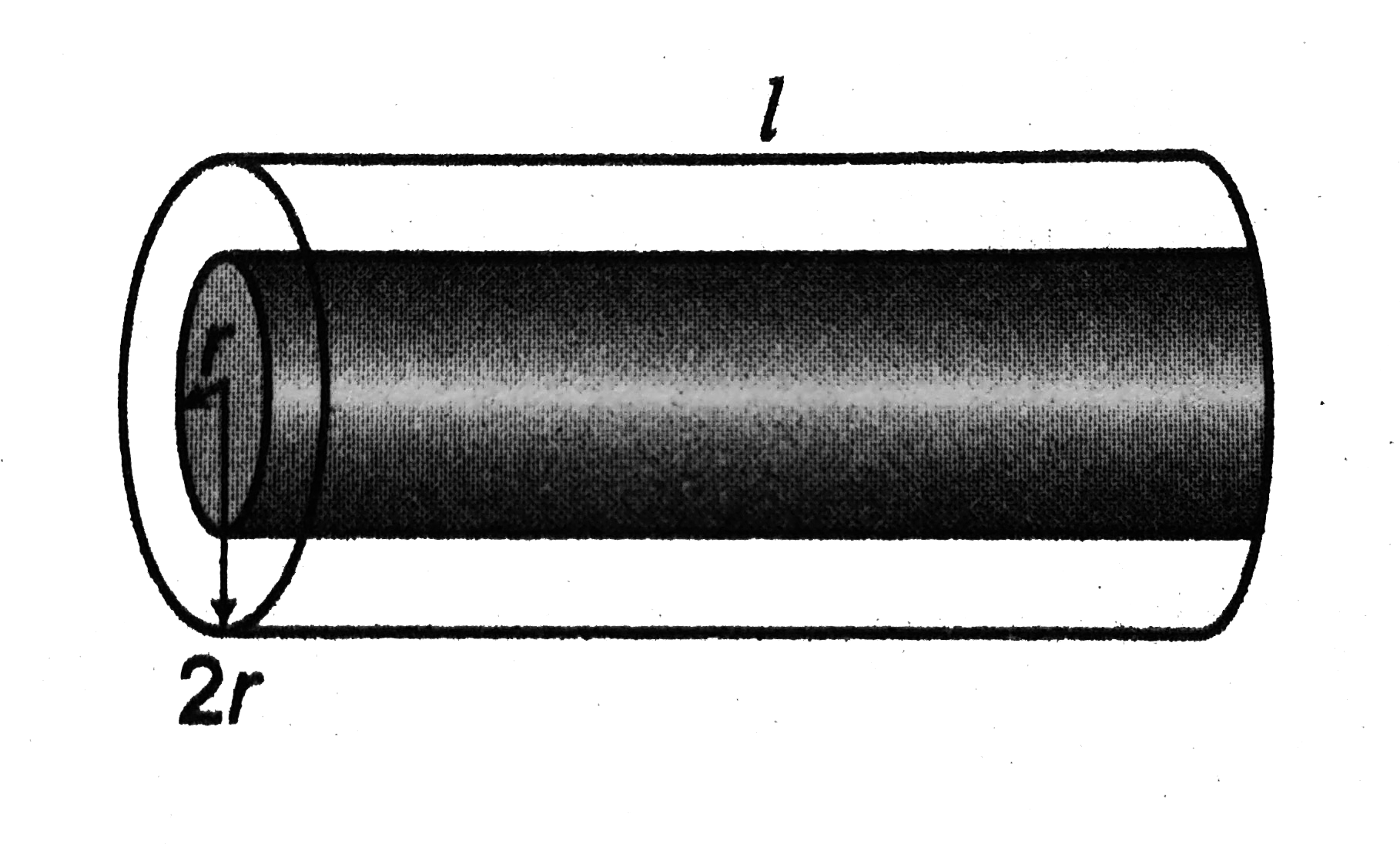
View SolutionA cylinder of radius R and length l is made up of substance whose thermal conductivity K varies with the distance x from the axis as `K=K_1x+K_2`. Determine the the effective thermal conductivity between the flat faces of the cylinder.
View SolutionA cube and a sphere of equal edge and radius, made of the same substance are allowed to cool under identical conditions. Determine which of the two will cool at a faster rate.
View SolutionA spherical ball of radius 1cm coated with a metal having emissivity 0.3 is maintained at 1000 K temperature and suspended in a vacuum chamber whose walls are maintained at 300 K temperature. Find rate at which electrical energy is to be supplied to the ball to keep its temperature constant.
View SolutionA body emits maximum energy at 4253 `Å` and the same body at some other temperature emits maximum energy at 2342 `Å`. Find the ratio of the maximum energy radiated by the body in a short wavelength range.
View SolutionA black body at 1500K emits maximum energy of wavlength 20000`Å`. If sun emits maximum energy of wavelength `5500Å`, what would be the temperature of sun.
View Solution
Exercise 1.3 questions and complete solutions for chapter CALORIMETRY of CENGAGE PHYSICS (HINGLISH) of Class 11