Complete Solutions to Exercise Subjective of chapter VECTORS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | VECTORS |
| CENGAGE PHYSICS | Exercise Subjective |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
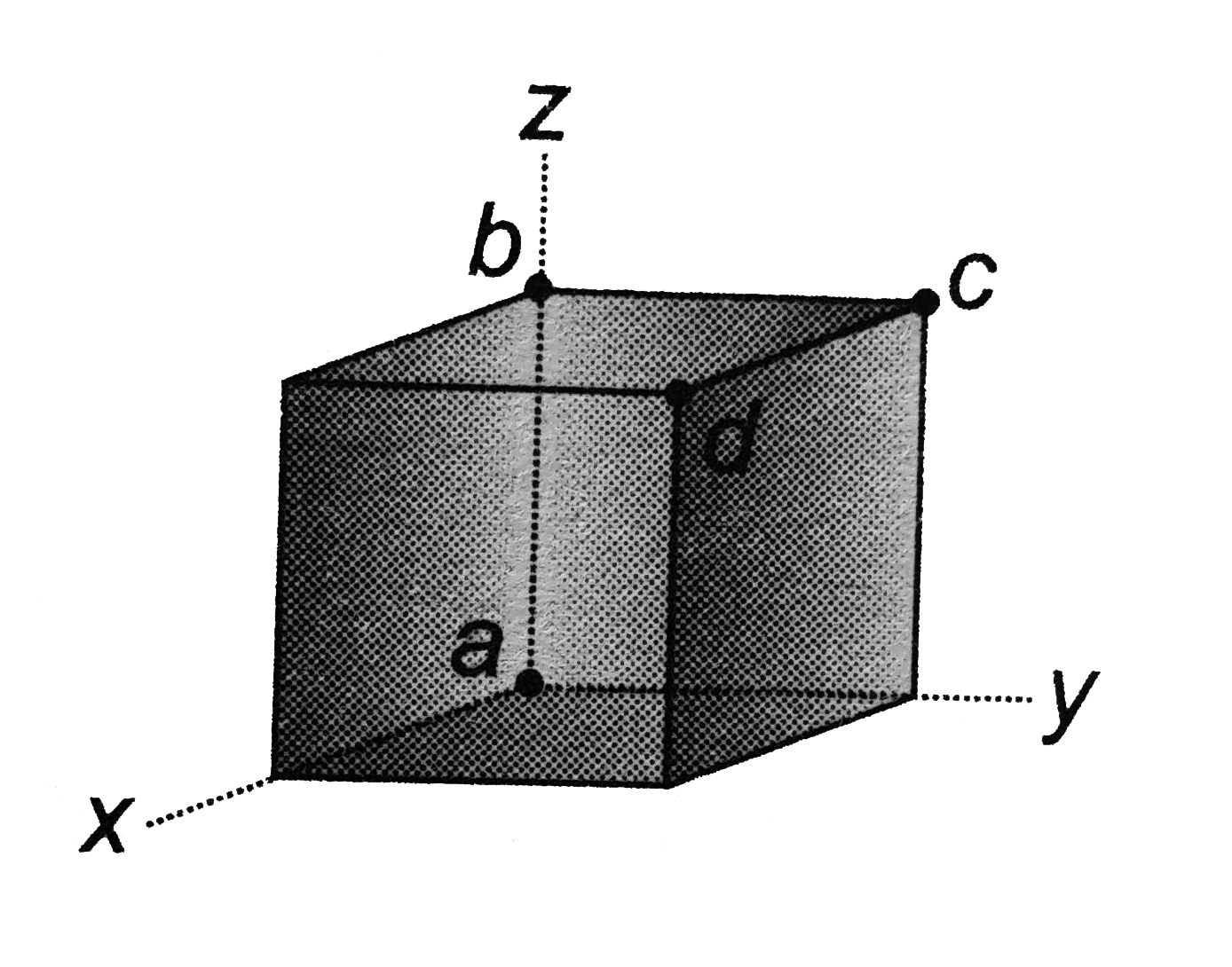
A cube is placed so that one corner is at the origin and three edges are along the x-,y-, and ,z-axes of a coordinate system (figure).Use vector to compute
a.The angle between the edge along the z-axis (line ab) and the diagonal from the origin to the opposite corner (line ad).
b. The angle between line ac (the diagonal of a face ) and line ad.
View SolutionYou are given vector `vec(A)=5hat(i)-6.5hat(j)` and `vec(B)=10hat(i)-7hat(j)`.
A third vector `vec(C )` lies in the `x-y` plane. Vector `(C )` is perpendicular to vector `vec(A)` and the scalar product of `vec(C )` with `vec(B)` is 15. From this information, find the component of `vec(C )`
View SolutionTwo vector `vec(A)` and `vec(B)` have magnitudes A=3.00 and B=3.00. Their vector product is `vec(A)xxvec(B)=-5.00hat(k)+2.00hat(i)`.
What is the angle between `vec(A)` and `vec(B)`?
View SolutionGiven two vectors `vec(A)=3hat(i)+hat(j)+hat(k)` and `vec(B)=hat(i)-hat(j)-hat(k)`.Find the
a.Area of the triangle whose two adjacent sides are represented by the vector `vec(A)` and `vec(B)`
b.Area of the parallelogram whose two adjacent sides are represented by the vector `vec(A)` and `vec(B)`
c. Area of the parallelogram whose diagnoals are represented by the vector `vec(A)` and `vec(B)`
View SolutionOn a horizontal flat ground, a person is standing at a point `A`. At this point, he installs a `5m` long pole vertically. Now , he moves `5m` towards east and then `2m` towards north and reaches at a point `B`. There he installs another `3m` long vertical pole . A bird flies from the top of the first pole to the top of the swecond pole. Find the displacement and magnitude of the displacement of the bird.
View SolutionFind the vector sum of `N` coplanar forces, each of the magnitude `F`,when each force makes an angle of `2pi//N` with that preceding it.
View SolutionCan you find at least one vector perpendiculr to `3hat(i)-4hat(j)+7hat(k)`?
View SolutionTwo forces P and Q acting at a point are such that if P is reveserd, the direction of the resultant is turned through `90^(@)`. Prove that the magnitudes of the forces are equal.
View SolutionUnit vector `hat(P)` and `hat(Q)` are inclined at an angle `theta`. Prove that `|hat(P)-hat(Q)|= 2 sin(theta//2)`.
View SolutionA sail boat sails `2km` due east, `5km 37^(@)` south of east, and finally an unknown displacement. If the final displacement of the boat from the starting point is `6km` due east,determine the third displacement.
View SolutionTwo forces of magnitudes P and Q are inclined at an angle `(theta)`. The magnitude of their resultant is 3Q. When the inclination is changed to `(180^(@)-theta)`, the magnitude of the resultant force becomes Q. Find the ratio of the forces.
View SolutionA vector `vec(B)` which has a magnitude 8.0 is added to a vector `vec(A)` which lies along the x-axis. The sum of these two vector is a third vector which lies along the y-axis and has a magnitude that is twice the magnitude of `vec(A)`. Find the magnitude of `vec(A)`
View SolutionThree vector as shown in (figure) have magnitudes `|vec(a)|=3,|vec(b)|=4`,and `|vec(c )|=10`
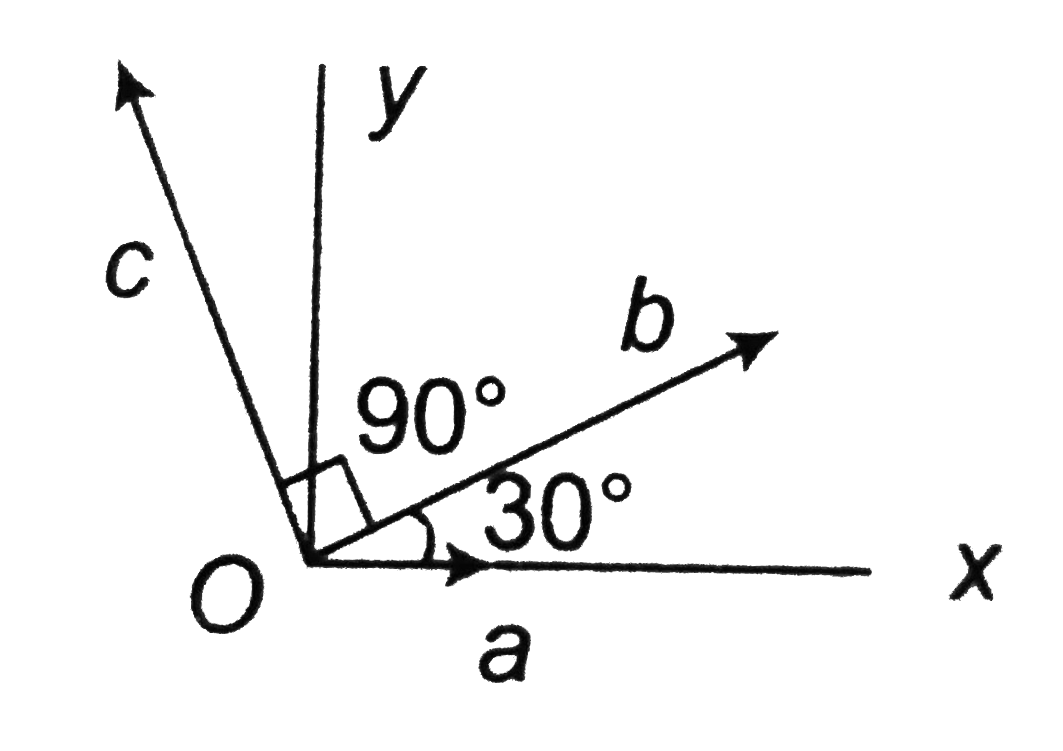
a.Find the `x` and `y` components of these vectors.
b.Find the numbers `p` and `q` such that `vec(c )=pvec(a)+qvec(b)`.
View SolutionA bouy is attached to three tugboats by three ropes. The tugboats are engaged in a tug-0f-war. One tugboat pulls west on the buoy with a force `vec(F)_(1)` of magnitude `1000N`. The second tugboat pulls south on the buoy with a force `vec(F)_(2)` of magnitude `2000N`. The third tugboat pulls northeast (that is, half way between north and east), with a force `vec(F)_(3)` of magnitude `2000N`
a. Express each force in unit vector from `(hat(i),hat(j))`.
b. Calculate the magnitude of the resultant force.
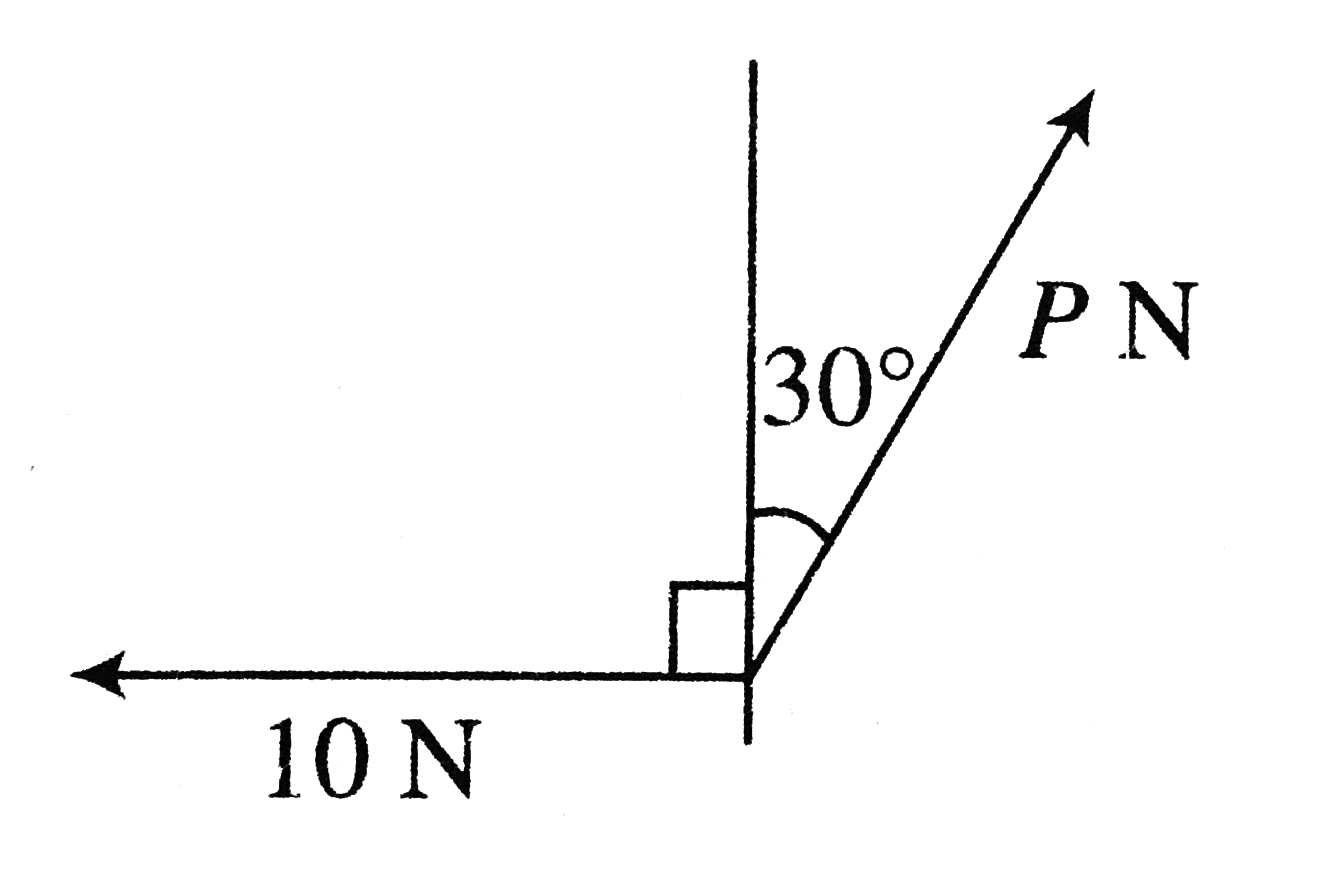
View SolutionTwo horizontal forces of magnitudes of `10N` and `P N` act on a particle. The force of magnitude `10N` acts due west and the force of magnitude `P N` acts on a bearing of `30^(@)` east of north as shown in (figure) The resultant of these two force acts due north. Find the magnitude of the resultant.
View SolutionThe position vectors of two balls are given by
`vec(r )_(1)=2 (m)i+7(m)j`
`vec(r )_(2)= -2(m)i+4(m)j`
What will be the distance between the two balls?
View SolutionA particle whose speed is `50ms^(-1)` moves along the line from `A(2,1)` to `B(9,25)`. Find its velocity vector in the from of `ahat(i)+bhat(j)`.
View SolutionA particle travels with speed `50ms^(-1)` from the point `(3,-7)` in a direction `7hat(i)-24(j)`. Find its position vector after `3s`.
View SolutionA particle has an initial velocity of `3hat(i) + 4 hat(j)` and an acceleration of `0.4 hat(i) + 0.3 hat(j)`. Its speed after `10s ` is :
View SolutionForces X,Y and Z have magnitudes `10N 5(sqrt(3)-1) N` and `5(sqrt(3)+1) N`, respectively. The forces Y and Z act in the same direction as shown in (figure) The resultant of X and Y and the resultant of X and Z have the same magnitudes. Find `theta`, the angle between X and Y.

View SolutionA particle of `m=5kg` is momentarily at rest at `x= at `t=. It is acted upon by two forces `vec(F)_(1)` and `vec(F)_(2)`. `Vec(F)_(1)=70hat(j)` N. The direction and manitude of `vec(F)_(2)` are unknown. The particle experiences a constant acceleration, `vec(a)`,in the direction as shown in (figure) Neglect gravity.
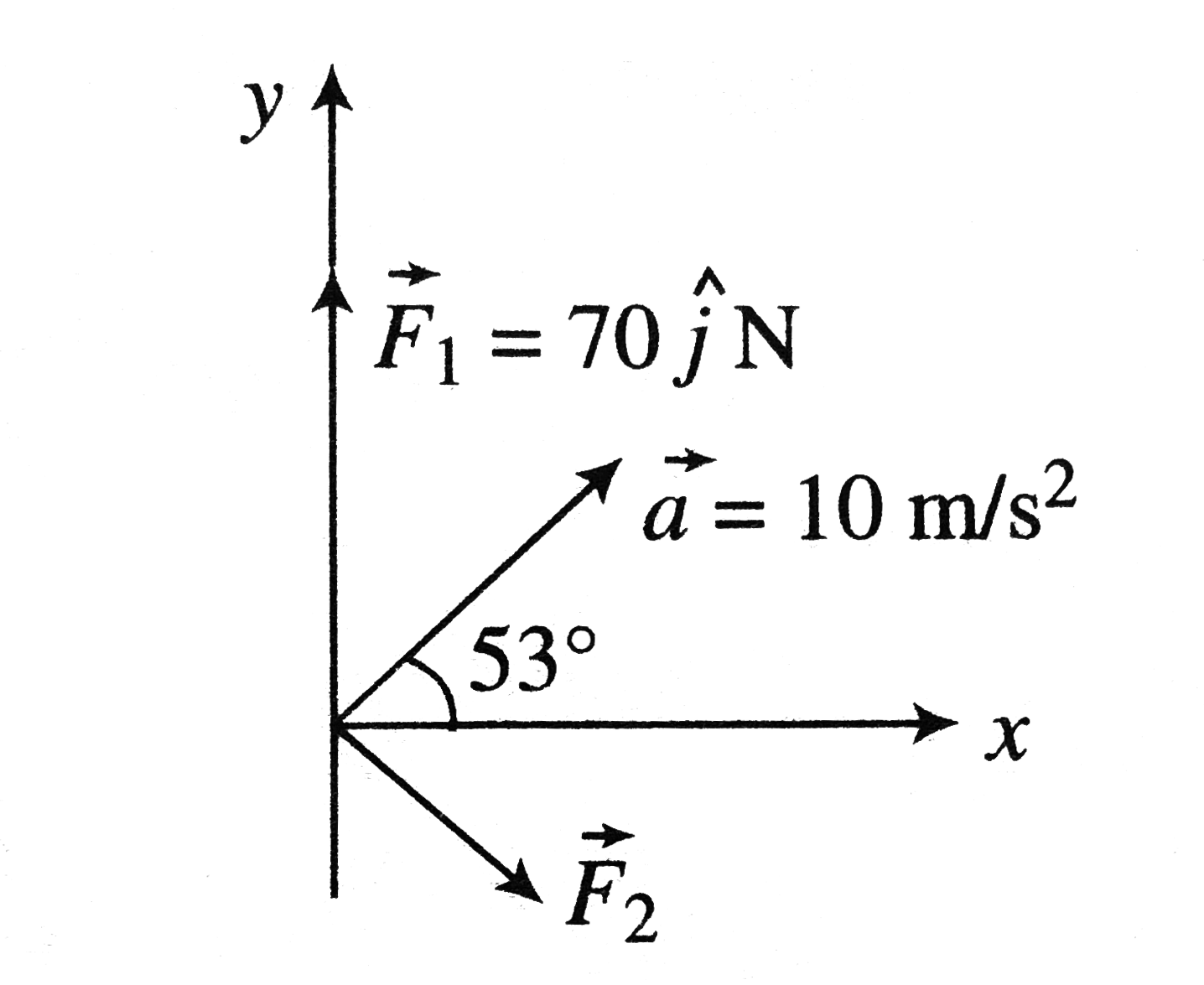
a.Find the missing force `vec(F)_(2)`.
b. What is the velocity vector of the particle at `t=10 s`?
c. What third force, `vec(F)_(3)` is required to make the acceleration of the particle zero? Either give magnitude and direction of `vec(F)_(3)` or its components.
View SolutionA spy plane is being tacked by a radar. At `t`=0, its position is reported as (100`m` ,200`m`, 1000`m`). 130`s` later, its position is reported to be (2500`m`,1200`m` ,1000 `m`). Find a unit vector in the direction of plane velocity and the magnitude of its average velocity.
View Solutiona. Calculate `vec(r )=vec(a)-vec(b)+vec(c )`, where `vec(a)=5hat(i)+4hat(j)-6hat(k)`,
`vec(b)= -2hat(i)+2hat(j)+3hat(k)`, and `vec(c )= 4hat(i)+3hat(j)+2hat(k)`.
b. Calculate the angle between `vec(r )` and the `z`-axis.
View SolutionA force `vec(F)=3hat(i)+2hat(j)+chat(k)`N causes a displacement `vec(r )=chat(i)+4hat(j)+chat(k)` `m`. The work done is 36 `J`. Find the values `(s)` of c.
View SolutionWhen two vectors of magnitudes P and Q are inclined at an angle `theta`, the magnitudes of their resultant is 2P. When the inclination is changed to `180^(@)-theta`, the magnitudes of the resultant is halved. Find the ratio of `P` and `Q`.
View SolutionFind the magnitudes of the unknown forces if the sum of all forces is zero (figure)

View SolutionThree boys are pulling a heavy trolled by means of three ropes. The boy in the middle is exerting a pull of `100N`. The other two boys ,whose ropes both make an angle `30^(@)` with the central rope, are pulling with forces of `50sqrt(3)N` and `100sqrt(3)N`. Find the magnitudes of the resultant pull on the trolltey.
View SolutionIf `vec(A)=2hat(i)+hat(j)` and `vec(B)=hat(i)-hat(j)`, sketch vector graphically and find the component of `vec(A)` along `vec(B)` and perpendicular to `vec(B)`
View Solution
Exercise Subjective questions and complete solutions for chapter VECTORS of CENGAGE PHYSICS (HINGLISH) of Class 11