Complete Solutions to Illustration of chapter VECTORS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | VECTORS |
| CENGAGE PHYSICS | Illustration |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
A car is moving round a circular track with a constant speed `v "of" 20 m s^(-1)` (As shown in figure).At different times,the car is at A,B and C,respectively . Find the velocity change (a) from A to C, and (b) from A to B.
 .
.
View SolutionThe greatest and least resulant of two forces acting at a point is `10N` and `6N`,respectively. If each force is increased by `3N`, find the resulant of new forces when acting at a point at an angle of `90^(@)` with each other .
View SolutionTwo equal vector have a resultant equal to either of them, then the angle between them will be:
View SolutionTwo forces whose magnitudes are in the ratio `3:5` give a resultant of 28N. If the angle of their inclination is `60^@`, find the magnitude of each force.
View SolutionThe resultant of two vectors `vecA` and `vecB` is perpendicular to the vector `vecA` and its magnitude is equal to half of the magnitude of the vector `vecB`. Find out the angles between `vecA` and `vecB`.
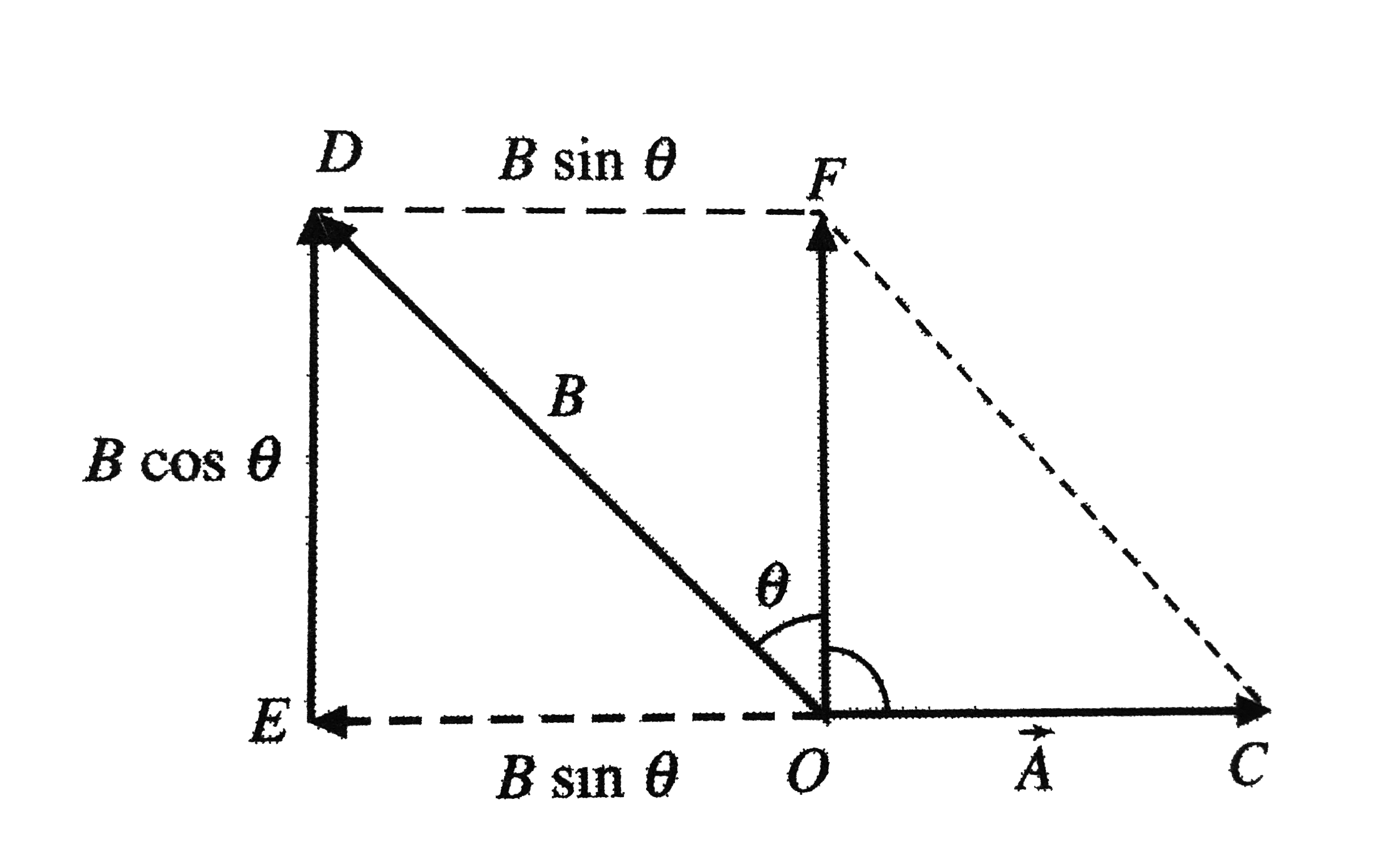 .
.
View SolutionTwo forces of unequal magnitude simultaneously act on a particle making an angle `theta (=120^(@))` with each other.If one of them is reversed ,the accelaration of the particle is become `sqrt(3)` times. Calculate the ratio of the magnitude of the forces.
View SolutionThe resultant of `vecP` and `vecQ` is `vec R`. If `vecQ` is doubled, `vecR` is doubled, when `vecQ` is reversed, `vecR` is again doubled, find P : Q : R,
View SolutionA particle slides with a speed of `3m s^(-1)` at P. When it reaches `Q`,it acquires a speed of `4m s^(-1)` after describing an angle of `60^(@)` at `O` as shown in figure .Find the changes in the velocity of the particle between `P` and `Q`. Assume that the path followed by the particle is circular from `P` to `Q`

View SolutionA force if `15N` acts on a box as shown in (figure).What are the horizontal component and vertical components of force?
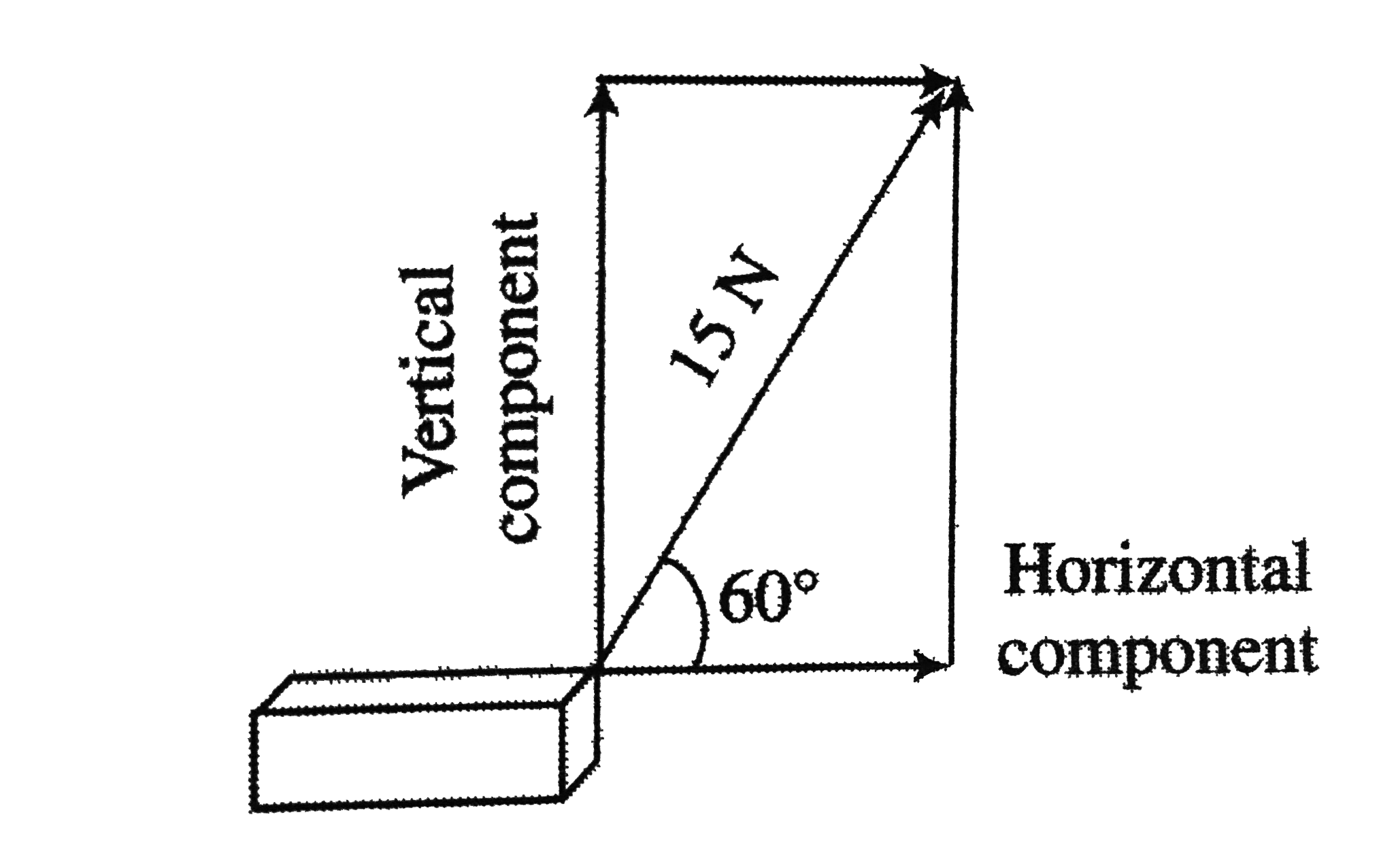
View SolutionA person in a wheelchair is moving up a ramp at constant speed.Their total weight is `900N`. The ramp makes an angle of `37^(@)` with the horizontal. Calculate the component of its weight parallel and perpendicular to ramp.

View SolutionA particle is moving with velocity `v=100m s^(-1)`. If one of the rectangular components of a velocity is `50m s^(-1)`. Find the other component of velocity and its angle with the given component of velocity.
View SolutionAn aeroplane takes off at an angle of `60^(@)` to the horizontal. If the velocity of the plane is `200kmh^(-1)`,calculate its horizontal and vertical component of its velocity (in `kmh^(-1)`) .
View SolutionA man rows a boat with a speed of `18Km h^(-1)` in the north-west direction (figure). The shoreline makes an angle of `15^(@)` south of west. Obtain the components of the velocity of the boat along the shoreline and perpendicular to the shoreline.

View SolutionFind the unit vector of `vec(A)=2hat(i)+3hat(j)+2hat(k)`.
View SolutionFind the unit vector of `(vec(A)+vec(B))` where `vec(A)=2hati-hatj+3hatk` and `vec(B)=3hati-2hatj-2hatk`.
View SolutionGiven `vec(A)=0.3hati+0.4hatj+chatk` calculate the value of c if A is a unit vector.
View SolutionDetermine that vector which when added to the resultant of `vec(A)=3hati-5hatj+7hatk` and `vec(B)=2hati+4hatj-3hatk` gives unit vector along y- direction.
View SolutionA car is moving in direction `vec(r)=-4hat(i)+3hat(j)` with a speed of `10m s^(-1)`. Write the velocity vector of car in unit vector notation.
View SolutionA car is moving with a speed of `10m s^(-1)`, If the east direction taken as x-axis and the north direction as y-axis . Write the velocity vector of car in unit vector notation.If it is moving (a) in the direction of N-E,(b) in the direction of `N-W`,(C ) in the direction of` S-W`, and (d) in the direction of `S-E`.
View SolutionAn inclined plane is inclined at `theta` with horizontal as shown in (figure).Write a unit vector in the direction parallel `(hat(a))` and perpendicular `(hat(b))` to inclined plane,in standard xy coordinate system.
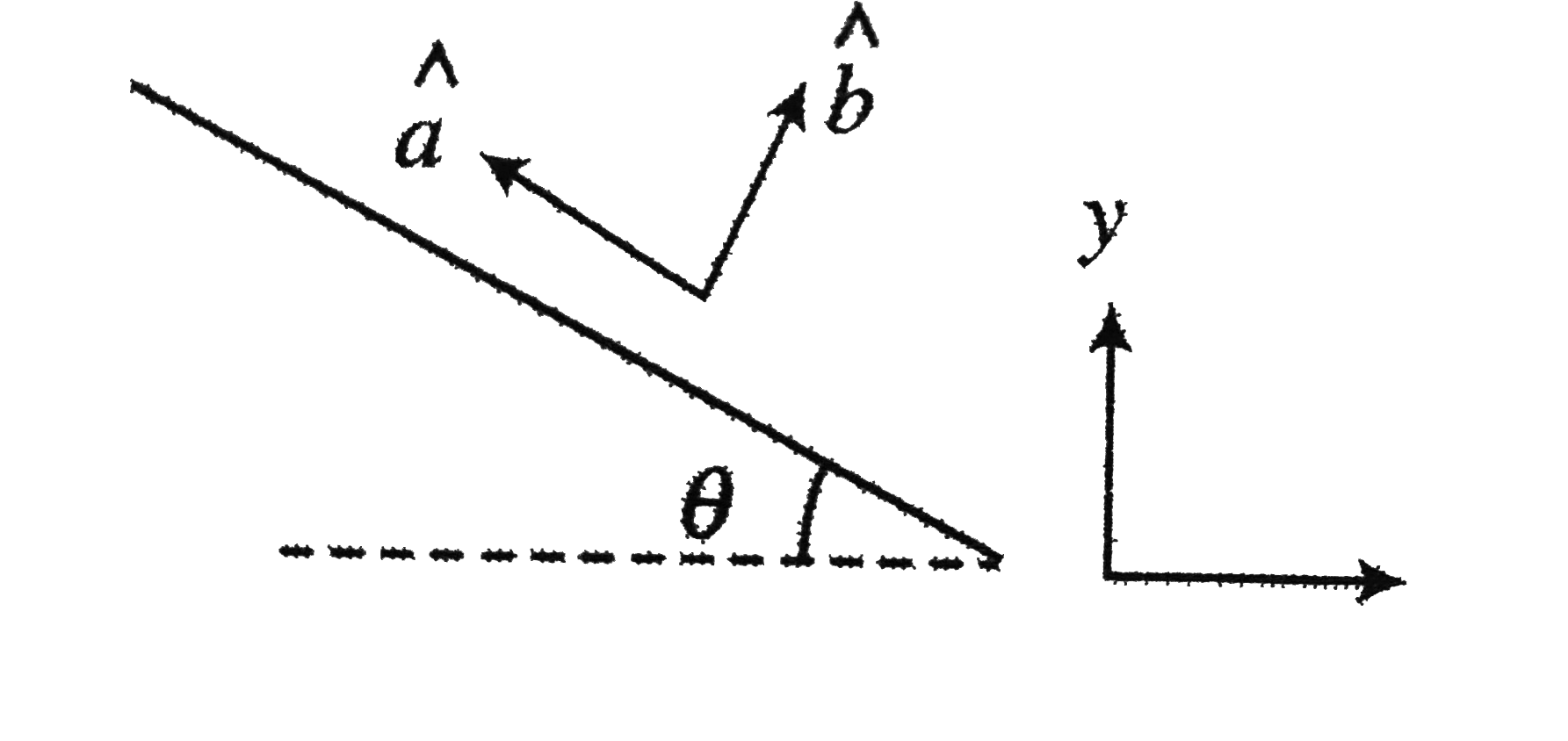
View SolutionGiven `vec(A)=5hat(i)+2hat(j)+4hat(k)`. Find (a) `|vec(A)|`
View SolutionA bird moves with velocity `20m s^(-1)` in a direction making an angle of `60^(@)` with vertical upward .Represent the velocity vector in a rectangular form.
View SolutionA particle is initially at point `A(2,4,6)m` moves finally to the point` B(3,2,-3)m`. Write the initial position vector,final position,and displacement vector of the particle.
View SolutionA bird flies due east through a distance of `100m`, then heading due north by a distance of `50m`, it flies vertically up through a distance of `20m`. Find the position of the bird relative to its initial position.
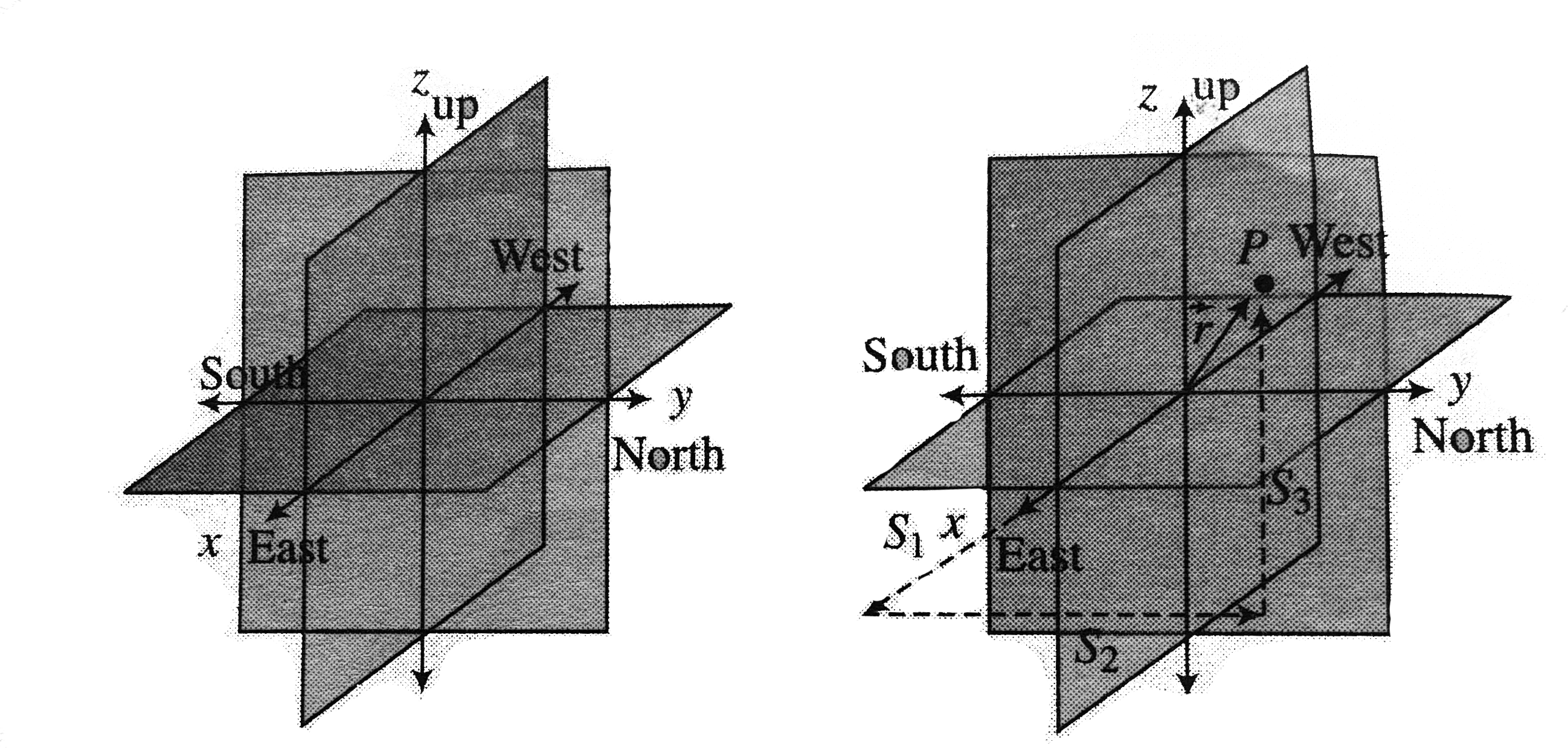
View SolutionAn insect crawls from `A` to `B` where B is the centre of the rectangular slant face. Find the (a) initial and final position vector of the insect and (b) displacement vector of the insect.
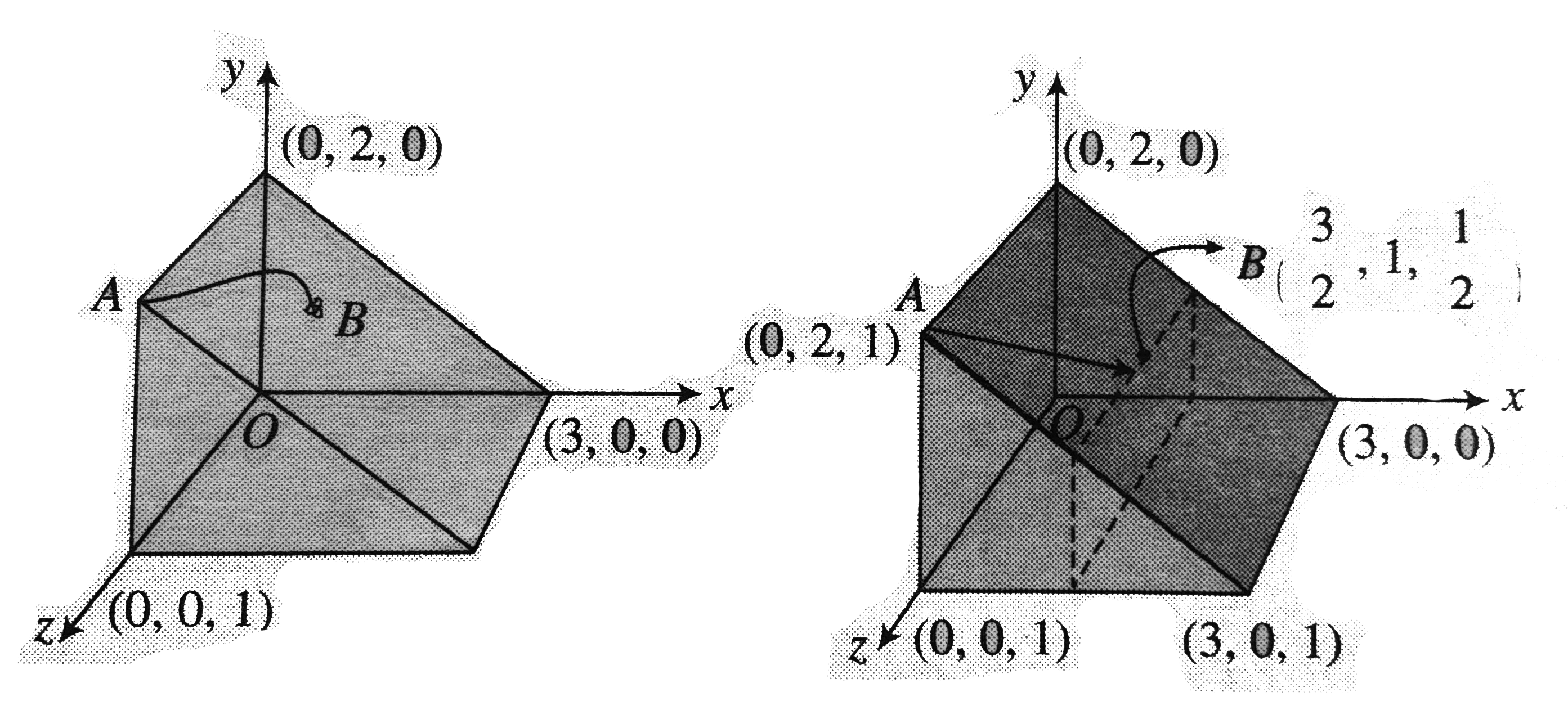 .
.
View SolutionGiven that `vec(A)+vec(B)+vec(C )=vec(0)`. Out of three vectors,two are equal in magnitude and the magnitude of the third vectors is `sqrt(2)` times that of either of the two having equal magnitude. Find the angles between the vectors.
View SolutionA bob of weight `3N` is in equilibrium under the action of two string 1 and 2 (figure) . Find the tension forces in the string.
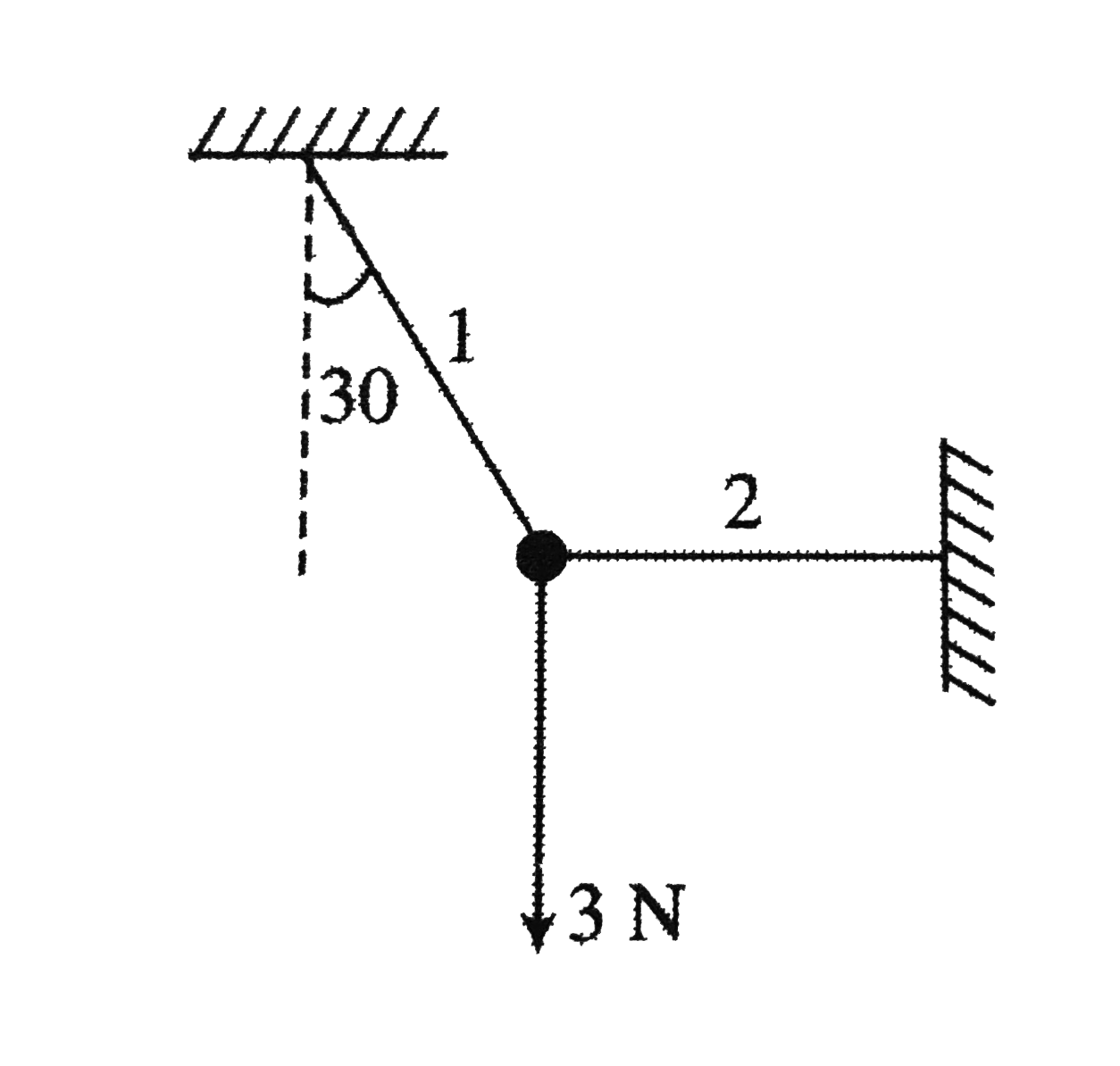
View SolutionFind the dot product of two vectors `vec(A)=3hat(i)+2hat(j)-4hat(k)` and `vec(B)=2hat(i)-3hat(j)-6hat(k)`.
View SolutionFind the value of m so that the vector `3hat(i)-2hat(j)+hat(k)` may be perpendicular to the vector `2hat(i)+6hat(j)+mhat(k)`.
View SolutionWhat is the angle between the following pair of vectors?
`vec(A)=hat(i)+hat(j)+hat(k)` and `vec(B)=-2hat(i)-2hat(j)-2hat(k)`.
View SolutionIf the sum of two unit vectors is a unit vector,then find the magnitude of their differences.
View SolutionFind the value of m so that the vector `3hat(i)-2hat(j)+hat(k)` may be perpendicular to the vector `2hat(i)+6hat(j)+mhat(k)`.
View SolutionProve that `(vec(A)+2vec(B)).(2vec(A)-3vec(B))=2A^(2)+AB cos theta-6B^(2)`.
View SolutionA body constrainedto move along the z-axis of a co-ordinate system is subjected to a constant force `vec(F)` given by `vec(F)=-hat(i)+2hat(j)+3hat(k)` newton where `hat(i),hat(j)`and `hat(k)` represent unit vectors along x-,y-,and z-axes of the system, respectively.Calculate the work done by this force in displacing the body through a distance of `4m`along the z-axis.
View SolutionBy vector method, prove that if the diagonals of a parallelogram intersect perpendicularly,then the parallelogram is rombus.
View Solution`hat(i)` and `hat(j)` are unit vectors along x-and y-axes respectively. What is the magnitude and the direction of the vectors `hat(i)+hat(j)` and `hat(i)-hat(j)`? What are the components of a vector `vec(A)=2hat(i)+3hat(j)` along the direction `hat(i)+hat(j)`and `hat(i)-hat(j)`?
View SolutionCalculate the are of the triangle determined by the two vectors `vec(A)=3hat(i)+4hat(j)` and `vec(B)=-3hat(i)+7hat(j).`
View SolutionCalculate the area of the parallelogram when adjacent sides are given by the vectors `vec(A)=hat(i)+2hat(j)+3hat(k)` and `vec(B)=2hat(i)-3hat(j)+hat(k)`.
View Solutiona. Prove that the vector `vec(A)=3hat(i)-2hat(j)+hat(k)`, `vec(B)=hat(i)-3hat(j)+5hat(k),` and `vec(C )=2hat(i)+hat(j)-4hat(k)` from a right -angled triangle.
b. Determine the unit vector parallel to the cross product of vector `vec(A)=3hat(i)-5hat(j)+10hat(k)` & `=vec(B)=6hat(i)+5hat(j)+2hat(k).`
View Solution
Illustration questions and complete solutions for chapter VECTORS of CENGAGE PHYSICS (HINGLISH) of Class 11